基于分形特征提取的电能质量数据挖掘

于燕平 林 涛

1(柳州铁道职业技术学院动力技术学院 广西 柳州 545616)2(武汉大学电气工程学院 湖北 武汉 430072)



基于分形特征提取的电能质量数据挖掘

于燕平1,2林 涛2

1(柳州铁道职业技术学院动力技术学院 广西 柳州 545616)2(武汉大学电气工程学院 湖北 武汉 430072)

发现“海量”监测数据中电能质量问题，并提取出有用信息，是电能质量有效治理的关键。将大数据挖掘技术应用于电能质量知识发现，8类电能质量数据先进行EMD分解，取前2阶IMF参数后结合分形理论分别求取计盒维、截距等10维特征参数。经泛化处理后，训练并生成了可靠的决策树，抽取出IF-THEN分类规则，用于电能质量问题预测。通过对比分析，分形参数较其他特征参数更有利于如振荡暂态、切痕、尖峰、闪变等电能质量问题分析，特别是对含噪电能质量的分析。结合大数据挖掘技术，不含噪和含噪信号的平均识别率分别提高了1.8%和4.1%。

数据挖掘 EMD分解 分形理论 决策树

0 引 言

现代工业技术的不断发展使得人们生活水平不断地提高，进而对电能质量和供电可靠性提出更严格的要求。近年来，世界各国为改善供电环境，都在积极地开发利用清洁、可再生能源。这些新能源并入原有的电力系统，会引起电压偏差、电压波动、闪变、谐波污染等一系列电能质量问题。如何有效地区分不同的电能质量问题，是提高电能质量的关键。

智能电网的深入建设，大量运营数据的积累，电力领域“数据大爆炸”的时代已经到来。面对每年数以千兆字节的海量数据，对数据的存储、分析和类型识别带来了巨大的挑战。电能质量识别主要包括特征提取和分类两个过程，特征参数提取的方法有S变换[1]、小波变换[2]、希尔伯特黄变换[3](HHT)等。电力系统实质是一个强非线性系统，存在着混沌机制和现象[4]，而分形理论可以抽象非线性系统发现其内在的规律性。近几年来，该理论逐渐的应用于电力系统分析领域。分类方法主要是基于传统数学统计和机器学习，如人工神经网络[5]、支持向量机等，这些分类方法的使用在电能质量识别方面取得了很大的成功。

面对日新月异的数据更新，从中发掘出有用的知识，如电能质量事件预测、故障识别、干扰源识别与定位和实时控制等。我们迫切需要寻找一种能够进行强大数据分析的方法——大数据挖掘，它以数据库和机器学习为技术支撑，进而对其进行继承与发展。大数据挖掘技术已经逐渐运用于电力各个领域，如电能消费趋势预测[6]、电力系统暂态稳定性预测[7]、火力发电机组的节能分析[8]等。

数据挖掘是从大量数据中抽取和挖掘出未知的、有价值的模式或规律等知识的复杂过程。文中根据IEEE有关电能扰动模型规定，结合MATLAB软件仿真了8类电能质量扰动信号。具体的挖掘过程如下：

(1) 运用希尔伯特黄变换(HHT)对8类电能质量扰动信号进行特征参数提取；

(2) 对提取的特征参数进行泛化处理作为决策树的输入，训练模型并产生规则；

(3) 对电能质量扰动信号进行模式识别；

(4) 扰动类型的深度知识发掘。

1 基于分形理论的电能质量特征提取

1.1 分形理论简介

分形理论是用于描述混沌信号有效地分析方法，其认为系统的各部分之间的几何结构都存在自相似性和标度不变性，这为其奠定了物理基础，从而得到了许多成功的应用。分形的度量方式有很多种，常用的有Hausdorff维、计盒维、相似维、关联维等。文中特征提取的是计盒维。

计盒维定义[9]设集合F⊂Rn，记Nε(F)是可以覆盖F的、边长为ε的n维立方体(记为εn-立方体)的最少个数，则F的计盒维数DB定义为：

(1)

计盒维的计算相对较容易，所以应用广泛，文中运用多点拟合来计算Db，步骤如下：

1) 取m个ε值，记为εi(i=1,2,…,m)。

2) 计算Nεi(F)。归一化电能质量扰动信号到单位立方形区域，即:F={s(t)|min(s(t))=0,max(s(t))=1,0≤t≤1}，其中s(t)表示归一化后电能扰动信号，取最小立方体的边长为ε，可知在区间In=[(n-1)ε,nε]内，覆盖F的最少正方体数为：

Nn=[(maxs(t)-mins(t))/ε]t∈In

则在[0，1]区间内覆盖F的总正方体的个数表示为：

(2)

3) 若令xi=log(1/ε)，yi=logNε(F)，分别计算点(xi,yi)，拟合直线y=kx+b,得到直线的斜率k即为计盒维Db，式中b为截距，即：

(3)

1.2 基于分形理论的特征参数提取

电力系统发生故障时，系统会不同程度地出现混沌现象。提取出有效区分各电能质量扰动信号的特征参数是获得好的识别结果的关键。本文采用MATLAB软件，随机生成8种电能质量扰动信号，分别是暂降、中断、谐波、振荡暂态、切痕、尖峰、暂升和闪变。采样频率2 KHz，数据长度取10周波，即为0.2 s，通过观察各扰动信号，提取出10维特征向量，具体提取过程如下：

1) 考虑信号幅度的变化规律，对输入电能质量扰动信号每周波求取最大值，得到10维的特征向量，然后再从这10维最大值向量中求取最大值和最小值，分别记为Max1、Max2；

2) 考虑信号经由变换后，分解为不同的频率分量后，有利于区分含有谐波成分的信号；因此，对输入信号进行经验模态分解(EMD)，取出前两阶IMF分量：IMF1、IMF2；

3) 分别对IMF1、IMF2提取出各自的能量分布E1、E2；

4) 分别求取IMF1、IMF2的过零率Zcr1、Zcr2；

5) 根据分形理论，分别计算IMF1、IMF2的计盒维Db和截距b，得到4个特征向量，分别为：K1、B1、K2、B2；

6) 文中为验证分形理论的优越性，将分别组合特征参数为：不含分形参数{Max1，Max2，E1，E2，Zcr1，Zcr2 }、含分形参数{Max1，Max2，E1，E2，Zcr1、Zcr2，K1，B1，K2，B2}2组特征向量。

2 决策树

2.1 决策树基本算法

决策树算法本质上是一种贪心算法，是以自顶向下递归的分治方式构造。树的每个内部结点代表对一个属性的测试，分支代表测试的每个结果，树的每个叶子结点就表示一个类别。

算法 Generate_decision_tree根据给定的电能质量扰动训练特征集生成决策树。

输入：训练特征参数的各属性数据均离散化处理，feature_list为候选属性集。

输出：决策树。

处理流程：

a. 创建一个结点N；

b. if 该结点中的所有样本均属于同一类别C，then

c. 返回N作为叶子结点，并标记为类别C；

d. if feature_list为空，then

e. 返回N作为叶子结点，标记为样本中的多数类别；

f. 从feature_list求取信息增益最大的属性test_feature；

g. 用test_feature标记结点N；

h. 对于test_feature中的每一个已知取值ai准备划分结点N所包含的样本集；

i. 由test_feature=ai产生结点N相应的分支，用以表示测试条件；

j. 设Di为test_feature=ai所获得的样本集合；

k. if Di为空，then 相应的叶子结点标记为样本中类别个数最多的类别；

l. else 叶子结点标记为：Generate_decision_tree(Di，feature_list-test_feature)endfor；

m. 返回N。

2.2 属性选择度量

属性选择度量是决策树的分裂准则，用以帮助确定生成每个结点时应采用的合适属性，常用的方法有信息增益、增益率和基尼指数等，本文选取信息增益。

设S是包含s个数据样本的集合，该集合中包含m种类别属性，不同的类别记为Ci，i={1,2,3,…,m}。设si为Ci类别中的样本个数，则对给定数据对象分类所需要的信息量定义为：

(4)

式中pi为数据对象属于类别Ci的概率。

3 仿真验证

本文数据由MATLAB 7.04随机生成8种不含噪的电能质量扰动信号共1610例，其中803例作为训练集，807例作为测试集；加入30 dB高斯白噪声的电能质量扰动信号共1240例，616例作为训练集，624例作为测试集。

3.1 特征参数值泛化处理

将提取出的特征参数保存于数据库中，这些数据包含了大量的细节性的数据信息，因此需要对这些数据进行更高层次的抽象以获得概要性的描述。提取的各类特征参数命名在数据库中就对应一个属性，则有条件属性C={E1,E2,Max1,Max2,Zcr1,Zcr2,K1,B1,K2,B2}，假设它们存在一个概念层次树，可以将它们划分为若干间隔(组)，本文根据数据的实际分布情况用等级进行划分，表1为含30 dB高斯白噪声的特征数据的泛化情况。

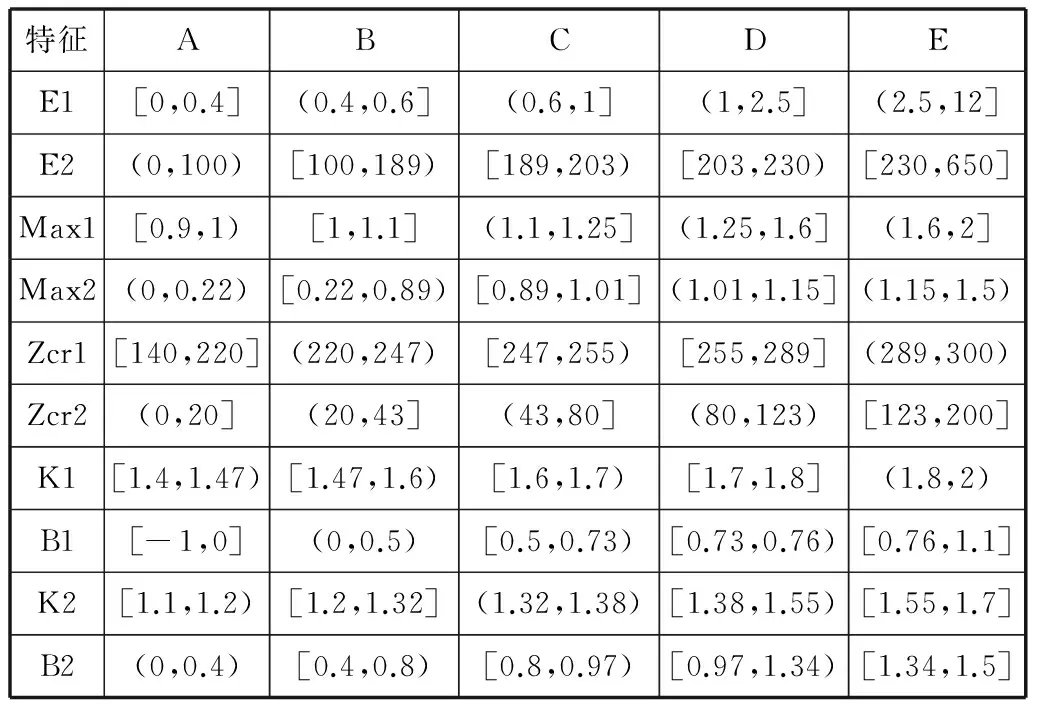
表1 含30 dB噪声的各类扰动特征参数值的泛化表示

表1中只列出了含噪特征参数的泛化情况，不含噪的特征参数的泛化类似。但是由于噪声的加入，前两阶IMF分量的过零率会有较明显的改变，特别是第一阶的IMF1分量，主要体现的是信号中的最高频的分量，加入噪声后IMF1就主要包括信号的突变部分以及大部分的噪声信号，直接导致过零率的大幅增加。

3.2 模型评估

建模过程中把训练集随机划分为70%训练部分和30%测试部分，将训练部分数据作为决策树的输入，计算信息增益选取合适的属性作为分支结点，构造决策树，利用测试部分数据对生成好的决策树进行准确性评估，训练集测试部分数据具体挖掘结果如表2所示。

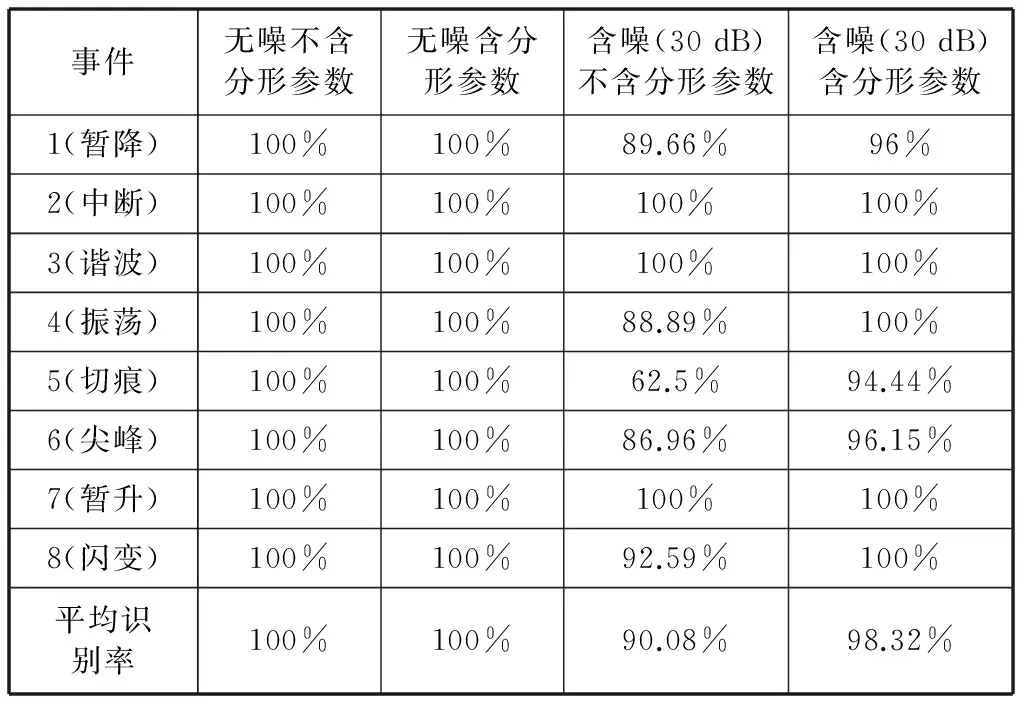
表2 电能质量扰动信号训练集测试部分挖掘结果

表2对训练集30%测试部分数据的挖掘结果：(1)不含噪声的各类扰动信号不论其特征参数是否含有分形参数，其识别率都为100%，实验说明对于不含噪声的电能质量扰动信号的分类识别，分形参数对识别结果的影响并不大；(2)对于含30 dB噪声的扰动信号，不含分形特征参数获得的识别率为90.08%，而含分形特征参数的特征集识别率为98.32%，结果表明，分形参数结合其他特征参数更有利于含噪声的电能扰动信号的识别；(3)训练集测试部分数据的识别结果说明已经构建了一个较可靠的决策树。

3.3 分类规则获取

决策树表示的分类知识可以被抽取出来并用IF-THEN分类规则形式表示，表3所示为含30 dB噪声的电能质量扰动信号决策树中抽取的部分分类规则。

表3 分类规则获取

分形理论研究的是非线性系统产生的不光滑和不可微的几何形体，表3的分类规则表明：(1) 对于电能信号(特别是加入噪声以后)波形出现振荡暂态、切痕、尖峰、闪变等现象时，分类决策就会不同程度地依赖于分形参数(计盒维数或截距)；(2) 对于带噪的谐波信号，经过EMD分解后，第一阶IMF噪声加载在高频分量上，反而导致IMF1的过零率较其他的信号低；(3) 对于短时电压变动类的电能扰动，如暂降、暂升、中断，它们更多地依赖与幅值变化相关的特征参数(如：max1,max2,E1或E2)。

3.4 知识验证及评价

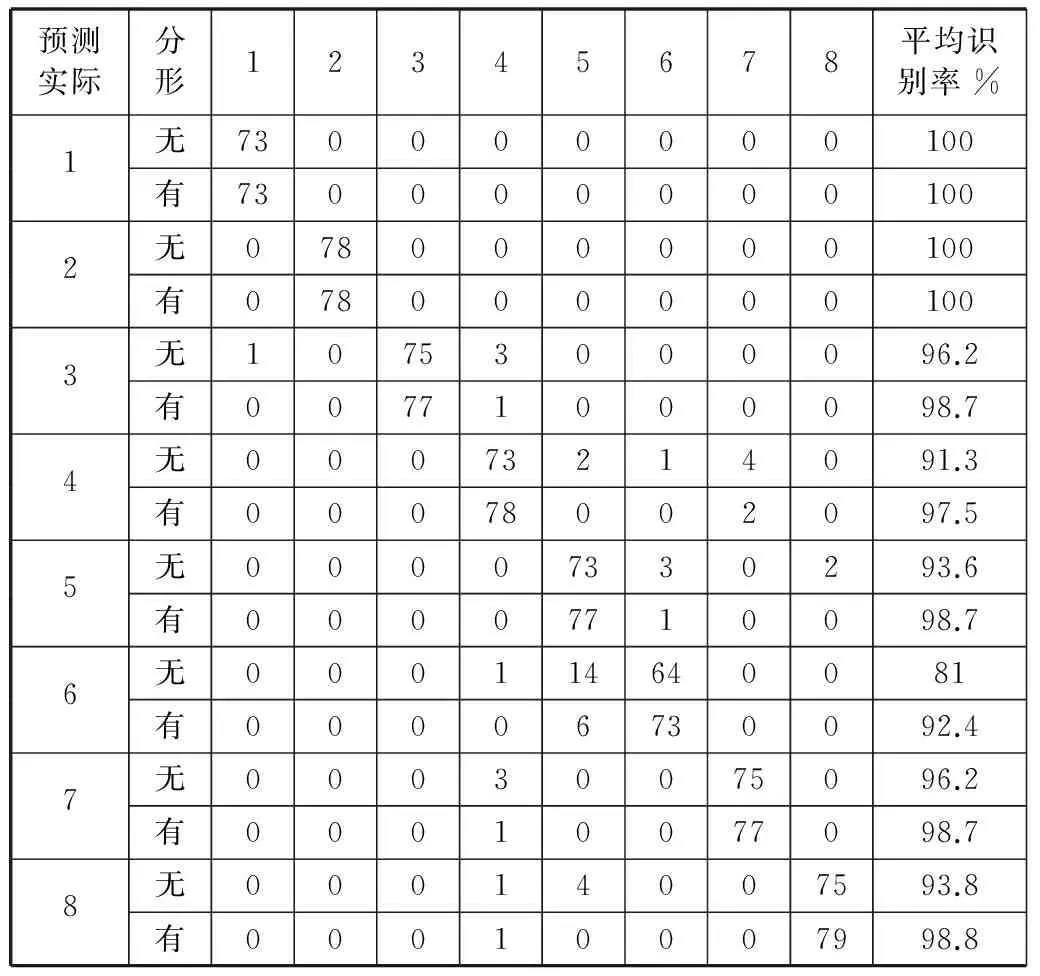
利用测试数据集对分类规则的预测准确性进行评估，分类结果如表4、表5所示。

表4 无噪声电能质量扰动信号(不含/含分形参数)测试集挖掘结果

表5 含30 dB噪声电能质量扰动信号(不含/含分形参数)测试集挖掘结果

预测实际分形12345678平均识别率%1无730000000100有7300000001002无078000000100有0780000001003无10753000096.2有00771000098.74无00073214091.3有00078002097.55无00007330293.6有00007710098.76无000114640081有00006730092.47无00030075096.2有00010077098.78无00014007593.8有00010007998.8

表4为不加噪声的电能质量扰动信号测试集评估结果，第1、2、3、7共4类扰动信号的识别率特征参数中不论是否包含分形参数都取得了100%的好结果。但从第4、5、6、8这几类的结果对比看，特征参数含分形参数较不含分形参数的特征参数的识别率都有所提高。

表5中对加入30 dB噪声的扰动信号的识别情况来看，不含分形参数的特征参数对第6类尖峰信号的识别有14例被误识为切痕信号，只取得了81%的识别率。而分形参数加入以后，取得了92.4%的识别率，有了较明显的提高，对于其他几类扰动信号(如类3、4、5、7、8)的识别率也有较大增长。仿真结果表明：与幅值变化相关的特征参数在扰动信号的识别方面，很容易造成如振荡暂态、切痕、尖峰等的误识，它们无法很好地区分各信号，当加入分形参数以后，这几类扰动的识别率有了明显改善，特别是在含噪声扰动信号的识别方面，体现了分形参数在描述不规则变化信号的优越性。

4 结 语

(1) 电力系统存在混沌机制，本文将电能质量扰动信号经由EMD分解结合分形理论应用于电能质量扰动信号的特征参数提取，提取出的向量作为特征集。为证明分形参数的有效性，分别对不含分形参数与含分形参数的特征参数进行了对比分析。实验结果表明，表征幅值变化的相关特征参数对振荡暂态、切痕、尖峰等信号的区分能力稍差，当加上分形特征参数后能有效地抽取出各扰动信号之间微小的差异性。较文献[10]对暂态闪变、尖峰、凹痕3类扰动的数据挖掘，本文有效地区分开8类电能质量问题。

(2) 借助大数据挖掘工具，为电力系统数据发掘提供了新思路、新途径。文中首先对特征数据进行泛化处理，应用决策树技术对电能质量扰动数据进行训练与预测，并抽取出部分的决策规则。含分形参数的特征集对电能质量扰动测试集的分类结果为：不加噪的平均识别准确率为99.09%，较不含分形参数的97.29%，识别率提高了1.8%；含30 dB噪声的平均识别率为98.1%，而不含分形参数的平均识别率只为94.01%，提高了4.1%，都取得了较好的分类结果。

(3) 本文中特征参数提取应用的大部分是全局性方法，造成了一定的误识情况。如表4中振荡暂态仍有5例被误识为暂升信号，表5中尖峰有6例误识为切痕信号等，表明提取出有效的、能抽取局部信息的特征参数将更有利于多类且相似度高信号的分类识别。

[1] Kumar R,Singh B,Shahani D T,et al.Recognition of Power Quality Disturbances Using S-Transform Based ANN Classifier and Rule Based Decision Tree[J].IEEE Transactions on Industry Applications,2015,51(2):1249-1258.

[2] 潘从茂,李凤婷.基于小波变换的暂态电能质量的检测与识别[J].电测与仪表,2013,50(11):69-72.

[3] 马慧君.希尔伯特—黄变换在电能质量检测中的应用研究[D].哈尔滨理工大学,2013.

[4] 何友全,肖建,熊启军.基于分形理论的电力系统高频暂态波形特征识别[J].电力系统自动化,2005,29(02):29-33.

[5] Biswal B,Biswal M,Mishra S,et al.Automatic Classification of Power Quality Events Using Balanced Neural Tree[J].IEEE Transactions on Industrial Electronics,2014,61(1):521-530.

[6] Yang Hang,Chen Huajun,Yuan Cai,et al.An Intelligent System for Forecasting the Trend of Consumed Electricity[C]// IEEE International Congress on Big Data (Big Data Congress).Anchorage,AK:IEEE,2014:.677-682.

[7] Tao X,Renmu H,Peng W,et al.Applications of data mining technique for power system transient stability prediction[C]//Proceedings of 2004 IEEE International Conference on Electric Utility Deregulation,Restructuring and Power Technologies.Hong Kong:IEEE,2004:389-392 .

[8] Yong-Ping Y,Ning-Ling W,Zhi-Wei Z,et al.Data mining-based modeling and application in the energy-saving analysis of large coal-fired power units[C]// 2010 International Conference on Machine Learning and Cybernetics (ICMLC).Qingdao:IEEE,2010:1095-1100.

[9] 韩培友,郝重阳,张先勇,等.基于模糊粗糙集、数学形态学和分形理论的医学图像分类研究[J].计算机应用研究,2004,21(2):241-245.

[10] Dash P K,Chun I L W,Chilukuri M V.Power quality data mining using soft computing and wavelet transform[C]//IEEE TENCON.Conference on Convergent Technologies for the Asia-Pacific Region.India,Kurukshetra:IEEE,2003:976-980.

POWER QUALITY DATA MINING BASED ON FRACTAL FEATURE EXTRACTION

Yu Yanping1,2Lin Tao2

1(DepartmentofPowerTechnology,LiuzhouRailwayVocationalTechnicalCollege,Liuzhou545616,Guangxi,China)2(SchoolofElectricalEngineering,WuhanUniversity,Wuhan430072,Hubei,China)

To find the power quality problems from "mass" monitoring data and to extract available information from it,this is the key to control the power quality effectively.We applied the big data mining technology to power quality knowledge discovery,exerted the empirical mode decomposition (EMD) on 8 kinds of power quality data in advance,took the first 2-order IMF parameters and then combined the fractal theory to calculate respectively 10-dimension feature vectors of box-counting dimension,intercept,etc.After the generalisation processing,they were trained and generated the reliable decision tree which was used to extract the classification rules of IF-THEN,and was used to forecast the power quality problems.By comparative analysis,the fractal parameters were more conducive to analysing the power quality problems such as oscillatory transient,notch,spike,flicker etc.,than other features,especially to the analysis of power quality signals with noise.Combining the big data mining technology,the average recognition rate of signals with and without noise increased 1.8% and 4.1% respectively.

Data mining EMD Fractal theory Decision tree

2015-07-06。国家自然科学基金项目(51177111)。于燕平，讲师，主研领域：电能质量分析与处理，信号处理。林涛，教授。

TP391.9

A

10.3969/j.issn.1000-386x.2016.11.006