呈现解法全貌 提升数学素养——一道立体几何题的5种解法与4个变式

●陆 峰 (杭州绿城育华学校 浙江杭州 310012)



呈现解法全貌 提升数学素养
——一道立体几何题的5种解法与4个变式

●陆 峰 (杭州绿城育华学校 浙江杭州 310012)

教师在一堂立体几何课上设计了一道求多面体体积的问题，它的5种解法帮助学生构建起求空间几何体体积的解法体系，4个变式又向学生呈现了一个问题产生与变化的过程，从而有效提升学生的数学素养．

立体几何;几何体体积;解法体系;数学素养

题目 如图1，已知正方体ABCD-A1B1C1D1的棱长为1，E为线段AB的中点，则四面体D1B1EC的体积为______．

解法1 利用空间向量工具求解(过程略)

点评 空间向量作为处理立体几何问题的一种有效工具，已成为学生解决立体几何问题的首选．本题空间坐标系容易建立，数据明确，大多数学生会选择此种方法求解．但不可避免会遇到空间向量解决立体几何问题的通病：计算繁琐、一处算错整题皆错．空间向量法对于学生空间想象能力、图形分析能力的培养也无多大帮助．

图1 图2

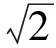
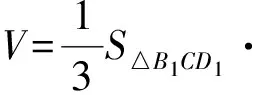
点评 本解法的关键在于视角的选择，将四面体视为三棱锥B1-ECD1，与将其视为三棱锥E-B1CD1在后续的计算中难度是不相同的．这一视角选择的过程实际反映了学生对图形的观察与分析能力的高低；其次在计算三棱锥高的过程中，学生又经历了空间几何体中线线、线面垂直的证明过程，切中立体几何的考查重点．

解法3 应用割补思想求解

如图3，取线段A1B1的中点J，联结D1J，EJ,则

VE-B1CD1=V正方体-VC-D1B1C1-VB1-EBC-VD1-ECD-VE-JB1D1-

点评 割补思想是求解空间几何体体积的一种常用方法，学生在分割、补全图形时经历了对图形中各个几何体形状及位置关系的分析判断过程，既培养了学生的空间想象能力，又培养了学生的图形分析能力．本题有多种割补方案，可引导学生多进行探索．

图3 图4

解法4 应用转换思想求解

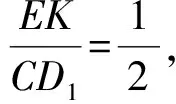
于是

VE-B1CD1=VB1-ECD1=2VB1-D1EK.

而

故

点评 较之解法2和解法3，解法4对学生的空间想象和图形分析能力要求有了更进一步的提升．“点K的选择、4点共面的确定”使学生经历了线线平行关系的判断与证明的思维过程，关系的得出又充分锻炼了学生的空间想象能力和计算能力．

解法5 应用等积变换思想求解

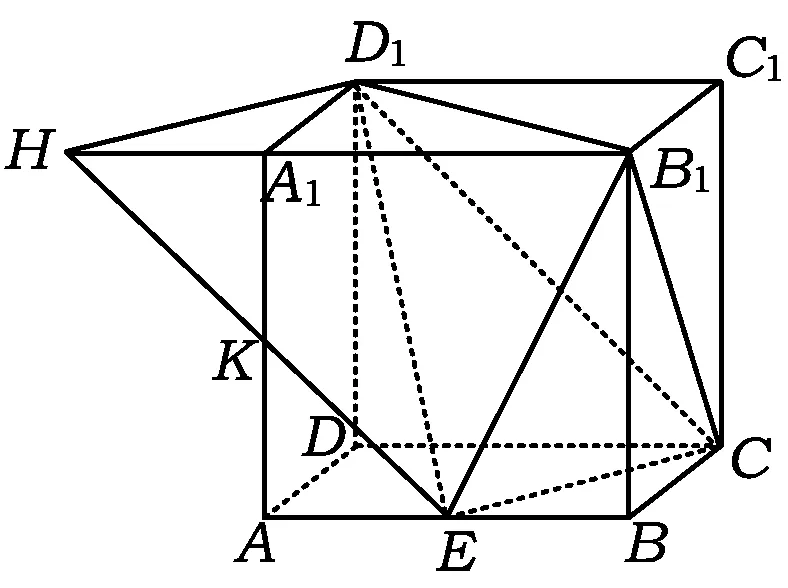
图5

如图5，取线段AA1的中点K，延长线段EK交线段B1A1的延长线于点H，联结D1H．因为EH∥CD1，所以EH∥面B1CD1，从而点E到面B1CD1的距离等于点H到面B1CD1的距离，于是VE-B1CD1=VH-B1CD1.而三棱锥H-B1CD1可转换视角为三棱锥C-B1D1H，故

点评 解法5可视为解法4的提升，它有2个特点：首先，它突破了立方体的框架，将直线和平面向立方体外的空间延伸，突出了空间特点，点亮了学生的思维；其次，它的计算过程非常简洁，可以通过口算完成，充分体现了浙江省立体几何“思维主导，计算靠边”的命题思路．

变式1 点E改变位置会怎样？

已知正方体ABCD-A1B1C1D1的棱长为1，E为线段AB的三等分点，则四面体D1B1EC的体积为______．

点评 变式1将点E从中点位置移动到了三等分点位置．一个点位置的改变导致四面体D1B1EC发生了哪些变化？原题的5种解法是否依然适用于解决本题？哪些解法将变得繁琐，哪些解法依然简洁？学生在解答上述问题的过程中进一步加深了对图形的理解，提升了空间想象能力．

变式2 点E运动会怎样？

已知正方体ABCD-A1B1C1D1的棱长均为1，E为线段AB上的动点，则四面体D1B1EC的体积的取值范围为______．

点评 变式2中的点E运动，使得原题从一个静止求值问题变成一个动态求范围问题，学生思维也从静变动．在求解时可以通过建立空间直角坐标系将问题转化为函数范围问题，也可通过探索点E的特殊位置分析点E运动对体积产生的影响．

变式3 改变底面形状会怎样？

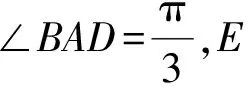
点评 变式3通过改变底面的形状来改变几何体的形状，可使学生直观感知几何体的变形过程，进而建立起几何体的变形模型．在探索变化及其解法时可引导学生讨论、分析四面体D1B1EC体积如何变化，促使学生形成新的解题感悟．

变式4 改变多面体形状会怎样？

点评 有了变式3的基础，变式4尽管几何体的形状进一步发生改变，学生依然能比较清晰地掌握图形的变化过程，正确地分析图形变换对所求问题产生的影响，进而寻求较为合理的解法．这就是我们常说的抓住了学生思维的“最近发展区”．

以上是一个例题的多种解法及变式的分析，它涵盖的面很宽，有知识体系、方法体系、思维体系、学法体系、教法体系．教学时向学生呈现解法全貌，促使学生形成较全面的解题体系，有利于学生更好地学习数学，提升学生的数学素养．

2016-01-27；

2016-04-06.

陆 峰(1977-)，男，浙江杭州人，中学一级教师，研究方向：数学教育.

O123.2

A

1003-6407(2016)06-28-02