偏相关分析在脉压相关因素研究中的运用*

贵州省疾病预防控制中心慢性病防治研究所（550001） 赵否曦 刘 涛

偏相关分析在脉压相关因素研究中的运用*

贵州省疾病预防控制中心慢性病防治研究所（550001） 赵否曦 刘 涛△

直线相关分析是数理统计中处理变量与变量之间关系的一种统计方法［1］。在多数情况下，变量之间是否存在因果关系并不被调查者所知的情况下，仅想了解两变量是否有相关变化关系，且这种依存关系的密切程度如何，这就是相关分析研究的范畴。从所处理的变量数目来看，两个变量间的相关称为简单相关；两个以上变量间的相关称为多元相关。从变量之间的关系形式上看，有线性相关分析及非线性相关分析。从统计思想和方法来看，线性相关是描述变量基本关系的统计方法。

在分析两个变量间相关关系时，必须将其他变量因素的影响考虑其中，这就需要运用偏相关系数进行变量间的相关性分析［2］。偏相关分析也称净相关分析，它在控制其他变量的影响下分析两变量间的线性相关性，所采用的工具是偏相关系数（净相关系数）。控制变量个数为一时，偏相关系数称为一阶偏相关系数；控制变量个数为二时，偏相关系数称为二阶相关系数；控制变量个数为零时，偏相关系数称为零阶偏相关系数，也就是简单相关系数。

本研究拟通过贵州省成人慢性病及其危险因素监测的调查数据，从运用的角度对简单相关分析与偏相关系数的结果进行解释，以说明偏相关分析在结果解释上的可靠性。

原理方法

简单相关分析是对两个变量之间的相关性进行分析，分析过程比较简单，用直线相关系数来展现变量之间的相关性强弱，直线相关系数也称Pearson积矩相关系数，用 r表示，计算式为［1］:

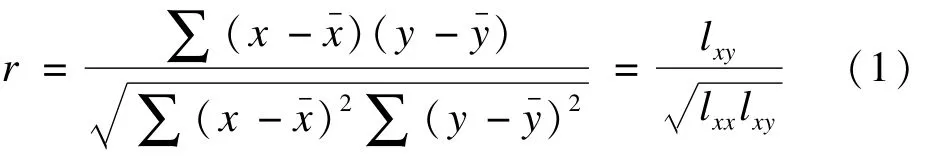
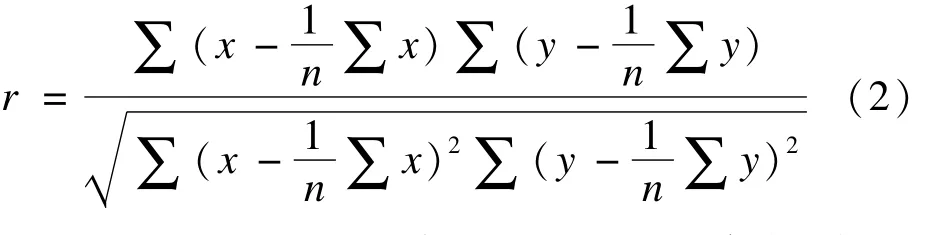
偏相关分析是控制了其他变量影响的条件，仅分析两个变量之间相关程度的过程，分析所得相关量为偏相关系数（或净相关系数）。偏相关系数可以利用简单相关系数进行表示，简单相关系数可以用式（2）计算而得。假设我们需要计算X和Y之间的相关性，Z代表其他所有的变量，X和Y的偏相关系数可以认为是X和Z线性回归得到的残差Rx与Y和Z线性回归得到的残差Ry之间的简单相关系数，即Pearson相关系数记为rxy·x1x2…xn

对于N阶偏相关系数的计算方法为:

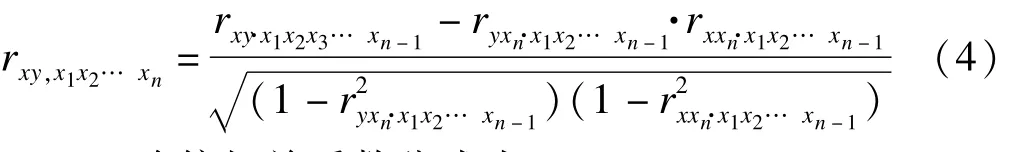
一阶偏相关系数公式为rx·yx1＝在控制x变量的情况下，分析x与y之间的相关关系。

二阶偏相关系数公式为rxy·x1x2＝，通过公式可以看出，是在控制了x1和x2变量后，对x与y之间的相关关系进行分析。

通过以上公式可以看出对于一阶偏相关系数可以利用三个变量之间每两个变量的零阶偏相关系数进行计算，二阶偏相关系数可用四个变量间的一阶偏相关系数进行计算。以此类推，N阶偏相关系数都可以通过N-1阶偏相关系数计算得出，对于有N个变量的偏相关系数可以利用进行两两组合得到零阶偏相关系数计算得出。

运用实例

近年来大量流行病学及临床研究表明脉压是心脑血管事件及不良预后的强烈预测及独立危险因素。脉压和大动脉顺应性对高血压预后及治疗的重要性越来越受到重视。对于老年人而言，脉压过宽对心脑血管的危害高于高血压对老年人的损害［3］，而脉压相关的因素与身体各项指标均有关，为探讨简单相关分析和偏相关分析在解释多个变量上的可靠性，本文以脉压及机体其他指标的相关性来解释变量之间的本质联系。

1.资料来源

资料来源于贵州省成人慢性病及其危险因素调查，调查采用多阶段随机整群抽样，共在贵州省范围内抽取12个县（区）开展，每个县（区）随机抽取4个乡镇（街道），每个乡镇（街道）随机抽取3个行政村（居委会），最终村与居委会随机抽取60户，每户按照KISH表抽取一位居民作为调查对象，考虑10%的无应答率，共计抽取9600例调查对象，经过数据整理并剔除无效问卷，最终调查对象共有9280例，调查内容包括基本情况，体格检查、实验室检查等。指标包括:脉压、收缩压、舒张压、体质指数、空腹血糖、餐后血糖、甘油三酯、高密度脂蛋白、低密度脂蛋白、胆固醇、腰围与睡眠时间。

2.分析结果

运用SPSS 22.0软件进行分析，将上述所有指标两两组合通过简单相关分析得出相关系数矩阵，在矩阵中可观测到脉压与所有变量均有相关性，然而值得注意的是，在多元统计分析中，由于变量间相关关系会受到更多复杂的因素影响，其相关程度并不能真实的反应脉压与其他指标的关联，（见表1）。通过矩阵可以看出，除脉压，其他变量间同样具有相关关系，甚至部分变量之间相关性超过了脉压，这就对评价脉压与其他变量之间的相关性造成影响。例如，脉压与舒张压的相关系数为0.269，而舒张压与收缩压的相关系数却为0.736，舒张压与脉压的相关性程度低于收缩压与舒张压的相关程度，但是脉压与收缩压的相关系数为0.830，这就可能说明，脉压与舒张压的相关程度是由于它们与收缩压的相关程度都比较高，但是两者本身可能并不存在相关性，或者是负相关关系。因为这种相关性被其他变量的强相关性所影响。因此，从这个例子可以看出，在多元统计分析时，简单相关系数常常无法反映变量之间的本质关系，这种解释并不可靠。

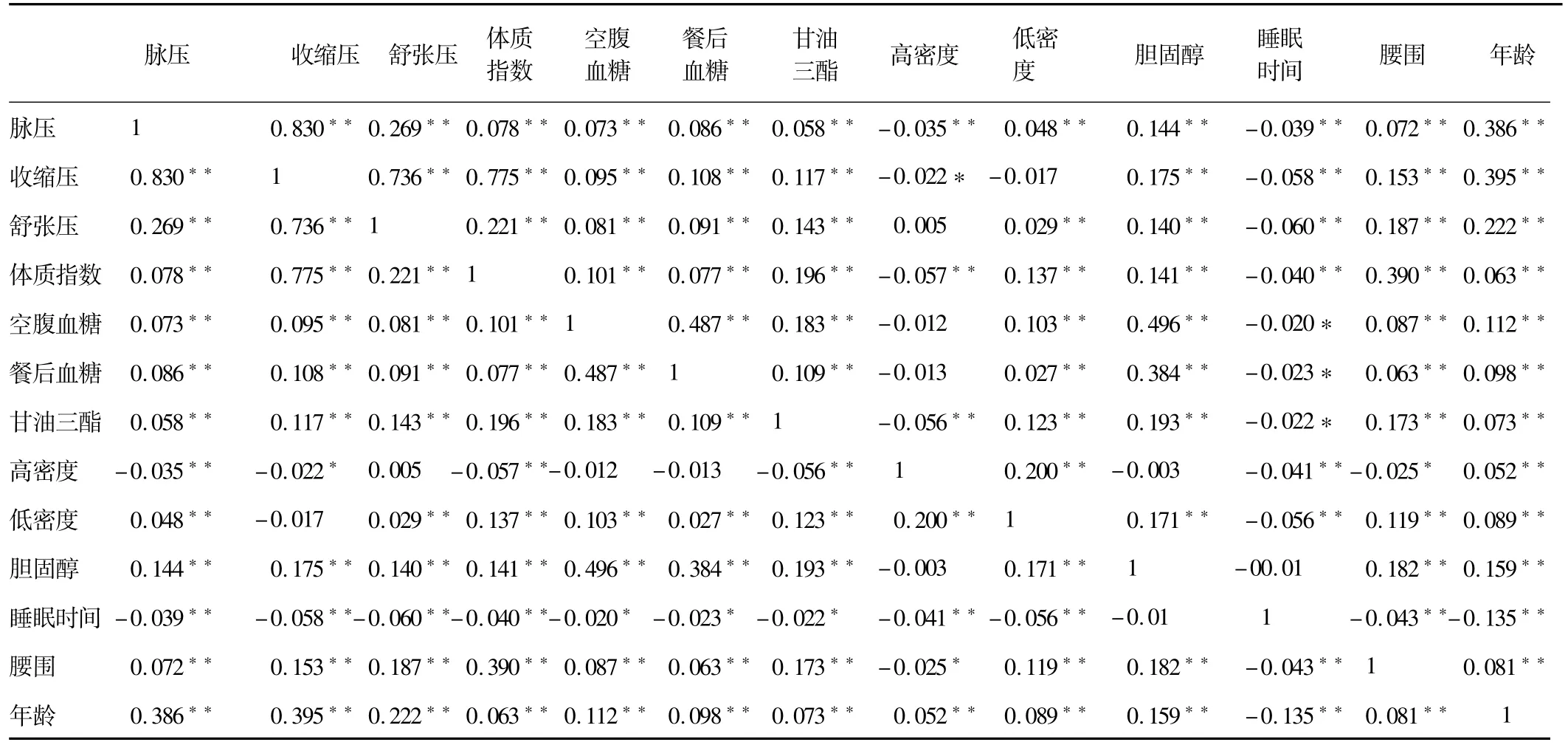
表1 脉压与各因素之间的简单相关系数矩阵

为了更加准确地描述脉压与其他变量之间的相关程度，我们运用偏相关系数在控制比较的两个变量之外的其他变量对它们的影响之后，计算脉压与各个变量之间的相关程度。

对比表2的数据，可以得到与表1一些不同的结论:收缩压、体质指数、低密度脂蛋白、胆固醇、睡眠时间与脉压的相关性较之简单相关系数有较大的提升，而空腹血糖、餐后血糖等指标相关性无统计学意义，而舒张压已由原来正相关变为了负相关。事实表明，在多元统计中，由于变量之间存在错综复杂的关系，偏相关系数与简单相关系数在数值上可能会存在很大差异，甚至会出现相关性相反的情况。

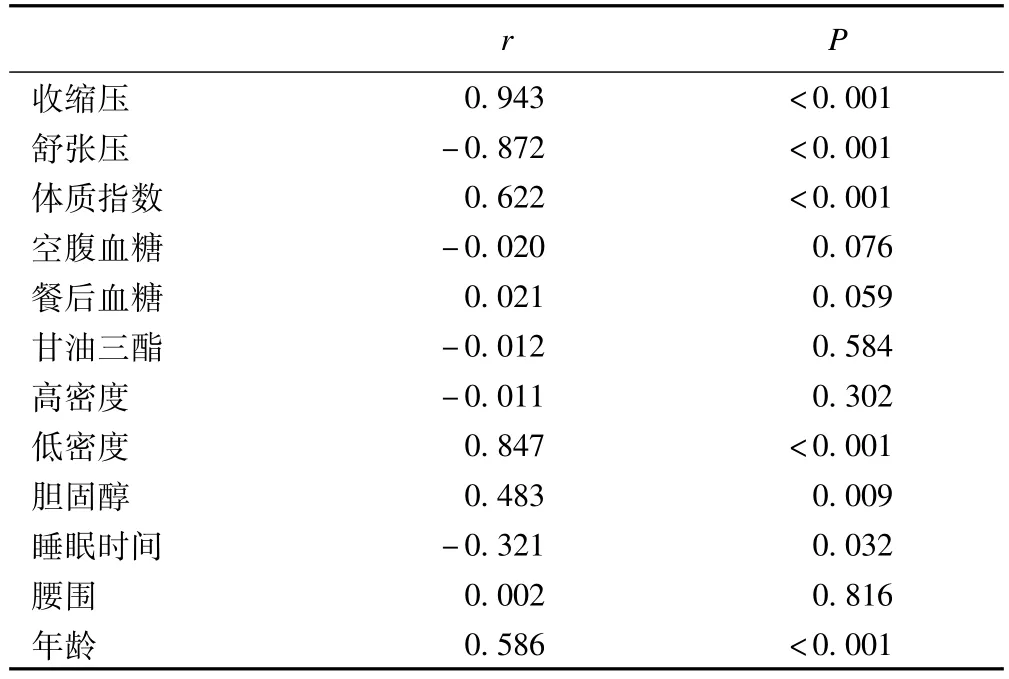
表2 脉压与其他因素的偏相关分析结果

讨 论

历史上对于相关性这一概念的首次提出，可追溯至Francis Galton对豌豆苗母代与子代的特性关系研究中。随后，Karl Pearson提出了Pearson相关系数，通过该系数来说明两个观察变量相关性的大小［4］。而随着回归分析与相关分析的不断深入，原来单变量之间的相关与回归已不能满足社会多元性发展的需要，因此多元统计分析得到了极大地发展，关于偏回归、偏相关的计算和运用正日益受到重视［5］。

本研究以脉压与其他因素的相关性作为研究切入点，运用简单相关系数与偏相关系数来分析脉压的相关因素，说明了偏相关系数对于解释具有多因素特点的调查数据在统计分析结果上的可靠性，但简单相关分析也并不是一无用处。通过计算简单相关系数的矩阵，不但可以直接得到任意两个变量的相关性大小，还可以挖掘其他变量之间各种复杂的偏相关关系，这对于解释和分析偏相关系数提供了更多的隐含信息。

本文的例子显示:脉压与舒张压之间的相关性，在控制了其他因素的影响后，其相关性变为负相关。这也提示两个变量之间的高度相关，有时并不是这两个变量本身的内在联系所决定，它完全可能由另外一个变量的媒介作用而形成高度相关。所以绝不能只根据相关系数很高，就认为两变量之间有直接内在的线性联系。此时要准确地反映两变量之间的内在联系需要考虑偏相关系数来进行解释。在多变量相关的场合，由于变量之间存在错综复杂的关系，因此偏相关系数与简单相关系数在数值上可能相差很大，甚至呈现负相关。

由脉压的计算公式可知，脉压的增高可由于两种情况导致，其一，收缩压增高，舒张压降低；其二收缩压、舒张压同时增高，但收缩压增幅高于舒张压。而在控制了其他因素的影响后，脉压与舒张压之间呈现负相关关系，也相比简单相关分析的结果更为可靠，这是因为:其一，脉压是收缩压与舒张压之差，是由两测量值得出数学差值。如果我们认同简单相关分析的结果，认为脉压的升高与收缩压和舒张压呈现正相关。就有可能提出“控制脉压的手段，在于有效地控制收缩压与舒张压的升高”的错误结论。其次，根据简单相关分析的结果，舒张压与脉压的正相关关系是建立在收缩压不断升高的基础上，然而通过研究我们发现，收缩压、舒张压与脉压随着年龄的增长均呈现了逐渐升高的趋势，如果不控制包括收缩压在内的因素对脉压的影响，就会得出舒张压越高，脉压就会越高的错误结论。而与脉压相关的其他因素中例如体质指数、低密度脂蛋白等在偏相关分析呈现的相关性也是通过控制了其他变量对其影响后的关联程度，其结果的真实性也较简单相关分析中所呈现的所有因素均相关要更加可靠。并且其中的关系也可在其他临床研究中得到证实［6－9］。

综上所述，在相关研究分析中，切忌根据简单相关的结果就武断认定研究的两因素具有相关性，尽管相关系数呈现的数值说明了他们之间的共同变化关系，并且这种关系在数学的体现上是计算正确的结果，但在很多情况下，这种共同变化关系很有可能是由某个或者多个因素的影响而引起的。因此，应引起重视的是当两个变量的相关性十分大时，尤其要注意他们之间的相关性是否符合逻辑关系，如果不符，就需要研究引起他们相关性的因素，通过去掉这些影响性后，计算“纯”的相关系数，从而发现其内在的线性关系。

［1］倪宗赞.医学统计学.北京.高等教育出版社，2003:138.

［2］李支元.数据挖掘系统中偏相关分析技术的应用研究.连云港师范高等专科学校学报，2012（4）:83-85.

［3］张大鹏，路方红，吴虹，等.脉压岁中老年急性心肌梗死价值的分析研究.中华心血管病杂志，2004，32（34）:368-369.

［4］JAldrich karl Pearson′s Biometrika:1901-36.Biometrika，2013，100:3-15.

［5］卢珊，王惠文，关蓉.相关系数矩阵的逆矩阵与行列式的内涵分析.数学的实践与认识，2015，45（6）:180-185.

［6］李抒云.身体质量指数与年龄对血压的影响.中国老年学杂志，2010，30:2439-2441.

［7］MR Garcia-palmicri，CJCrespo，DM Gee.Wide pulse pressure is an independent of cardiovascular mortality in Puerto Ricanmen.Nutritiony Metabolism＆Cardiovase Disease，2005，15（1）:71-78.

［8］邓光瑞，黄光胜.高血压心血管事件的脉压预测研究.吉林医学，2010，22（8）:921-922.

［9］马松.脉压对高血压心血管事件预测的临床价值.航空航天医学杂志，2010，22（8）:658-660.

（责任编辑:郭海强）