多水平分析在调查问卷结果分析中的应用

国家医学考试中心（100097） 杨芳丽 何 佳

多水平分析在调查问卷结果分析中的应用

国家医学考试中心（100097） 杨芳丽 何 佳△

目的探讨应用两水平分层logistic回归模型分析调查问卷二分类结局变量资料的影响因素，对影响因素做出正确的评价和解释。方法以学生的调查问卷作为分析对象，运用两水平分层logistic回归模型，拟合一系列零模型、随机截距模型，识别学生水平和学校水平因素的影响大小。结果学生对所研究问题的看法受到学生个体特征和学校特征的影响，学生层面中学生成绩影响较大。结论多水平分析方法是处理分层嵌套数据的有用工具，利用两水平分层logistic回归模型可以同时探讨学生层面和学校层面解释变量对结局变量的效应，对于分析嵌套数据结构资料结局变量的影响因素有优越性。

多水平分析 二分类资料

观察对象对事物或现象的看法并不是一种稳定不变的个人特质，会受到对所处环境感知和认识的影响。也就是说，在不同的环境，观察对象有可能表现出不同的看法。因此，当研究环境设定在学校，观察学生对研究指标的应答，就不能忽略学校的教育教学环境影响。而这样的数据往往具有层次性，即学生嵌套于各自的班级，班级又嵌套于不同的学校。这样学生个体之间就不是相互独立的，而是受到其所嵌套单位特征的影响。以往对这类数据的分析常在个体水平或较高水平的单一水平上分别进行数据分析，分析时忽略了数据的多层结构。传统的回归分析假设各个观察单位是相互独立的，但是这不符合多层结构数据的实际情况，因为在多层结构数据中，同一组内的个体与其他组的个体比较有更大的相似性，各组内的观察单位不是相互独立的，如果仍然使用传统回归模型进行分析，可能出现错误拒绝有统计学意义差异的真假设［1－2］；在使用较高水平的数据进行分析时又会因为样本量的减少，导致统计效能降低。

本文以调查问卷的调查指标为例，采用两水平分层logistic回归模型，在综合考虑学生个体和学校层面特征影响的前提下，以定量方式探讨学生个人特征和学校环境因素对调查指标的影响。

资料来源

本文所用数据为2015年14所医学院校临床医学专业4年级（5年制）和5年级（长学制）的4396名在读本科学生参加的国家医学考试中心统一组织的临床执业医师资格分阶段考试实证研究考试，以及考后学生填写的调查问卷。问卷全部收回后进行仔细甄别，剔除回答不完全的问卷，共获得有效问卷3937份，有效回收率为89.56%。

研究方法

本文对数据使用MLwiN 2.02拟合两水平分层logistic回归模型，分析调查指标的结局变量在不同层次间的分布，并尝试检验学生和学校不同层次变量的影响。

两水平分层logistic回归模型的完整公式为:

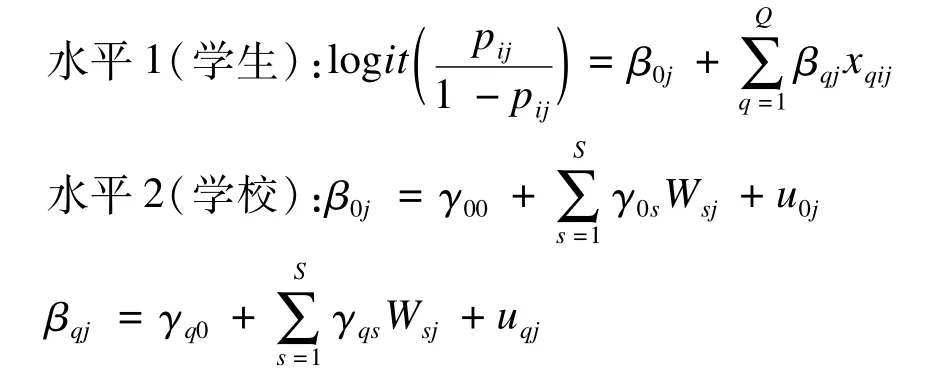
pij为调查指标的结局变量为“是”的概率，“ij”代表第j所学校第i名学生，β0j为水平1的随机截距，βqj是水平1的随机斜率，γ00是结局变量选择”是”与选择”否”总平均概率比的自然对数值，u0j代表第j所学校的平均概率比自然对数值与总平均概率比自然对数值间的差异。βqj为学生水平解释变量xqij的随机效应参数，Wsj是水平2变量。

本研究主要通过拟合一系列两水平模型探讨研究问题。首先，利用零模型分析14所院校之间调查指标的结果是否存在显著差异；其次，通过一系列随机截距模型确定哪一些学生层面和学校层面的指标纳入分析，最后，拟合出最终的模型分析学生个体变量对调查指标的影响，以及这些影响在不同学校之间的变异。

调查问卷共设计了20个问题，既包含学生对考试客观特性方面的感受和了解，如对考试难易程度的感受；也包括学生对考试的主观性判断，如对试题覆盖面的理解等；还对考试前的准备、感受以及考试时的感受等进行调查。本研究采用问卷调查结果，对四个问题进行分析:①对本次考试内容是否熟悉；②本次考试所考查的内容80%以上是否与教学重点内容一致；③是否认为本次考试试卷整体难度较大；④是否认为使用临床场景的病例型试题考查基础医学知识增加了试题难度。结局变量为学生对以上问题的回答（1:是/0:否）。

本研究收集学生层面（即水平1）的变量有学生性别、学制、年级、所学专业（均为临床医学）、本次考试成绩在全体学生中百分等级；学校层面（即水平2）的信息包括学校类型、学校所处的地区、学校此次考试平均成绩在14所院校所处位置、学校中女生比例。使用虚拟变量编码类别变量，其中性别中男性＝0，女性＝1；学制分为5年制、6年制、7年制和8年制，以5年制为对比组；年级中4年级＝1和5年级＝0；本次考试成绩在全体学生中百分等级分为处于下25%、中间50%、上25%三种，以下25%为对比组。学校类型分为“985/211”院校和其他本科院校；根据地理位置和经济发达程度把学校所处区域分为东部、中部和西部，以东部为对比组；学校此次考试平均成绩在14所院校所处位置分为处于下25%、中间50%、上25%三种，以下25%为对比组。

结 果

1.描述性统计结果

本研究共有14所院校3937名学生，女性学生（55.80%）多于男性学生（44.20%）。以5年制学生为主，占到总人数的90.40%。学生中4年级最多，占到94.79%。14所院校中985/211院校共4所，占28.57%，其余10所院校是一般本科院校。院校分布地区在东部的最多，为8所，占总数的57.14%，中部和西部各3所。

2.零模型参数估计结果

零模型是模型分析的第一步，此模型仅有一个随机截距而没有任何解释变量。是否有构建多层模型的必要性，可以结合专业判断，以及使用VPC（variance partition coefficient）进行度量。多水平模型的组内相关系数可以测量组内个体是否独立［3］。两水平分层logistic回归模型的VPC，因为水平1的方差依赖于模型中解释变量的值，因此不能使用组内相关系数来计算。本研究中采用公式估计VPC。对所分析的4个调查指标分别拟合零模型，表1为拟合结果。从表1可知，四个调查指标零模型的水平2方差P值均小于0.05，表明同一学校内学生的回答情况比不同学校间学生的回答情况更为相似，各学校间学生平均回答情况有显著差异，学校层次结构不能忽略，因而需要采用多水平模型。4个调查指标的 VPC值分别为 0.050、0.037、0.033、0.043，结果显示各调查指标平均回答情况总变异中分别有5.0%、3.7%、3.3%、4.3%来源于学校之间的差异。虽然学校层面的方差占总方差的比例不是很大，但是有研究显示，即使是很小的组内相关系数也可能增加犯第一类错误的概率，加之研究问题具有明显的层次特征，因此有必要进行分层logistic回归模型分析［5］。

表1 两水平零模型参数估计结果

3.完整模型参数估计结果

在零模型分析后，拟合了一系列随机截距模型，确定学生个体层面的哪些变量影响同一学校学生对调查指标回答情况，哪一些变量的回归系数在学校之间可能不同。经过分析发现，学制与结局变量没有关系，故最终模型中不纳入学制。另外，与结局变量没有关系的变量，问题1是性别，问题2是年级，问题3与问题2相同；问题4是性别、年级，但是本研究的目的不是预测，而是观察解释变量对结局变量的影响，故在最终模型中纳入性别、年级、成绩百分等级变量。学校层面的变量中仅纳入“是否985/211院校”变量，学校中女生比例、学校所在地区、学校此次考试成绩在14所院校所处位置的类别不纳入模型。表2是最终的两水平回归模型结果。

由表2可知，在控制其他因素不变的情况下，对本次考试的熟悉程度方面，学生成绩的回归系数有统计学意义，学生成绩百分等级处于上25%学生和中间50%学生分别与下25%学生相比熟悉程度的OR估计值为1.483和1.281（P＜0.05）；上25%学生比中间50%学生的熟悉度的OR值是1.157（P＞0.05）；性别和年级的回归系数均无统计学意义（P＞0.05）。学校层面上，985/211院校学生比一般院校对于本次考试的熟悉度OR值为0.593，呈边际统计学意义（marginally significant）（P＝0.048）。

对于本次考试所考查内容80%以上知识点是否与教学重点内容一致，性别和学生成绩百分等级的回归系数有统计学意义（P＜0.05）。女生比男生认为一致的OR值是1.181，学生成绩百分等级处于上25%的学生和中间50%的学生比下25%学生认为一致的OR值分别是2.197和1.654、上25%的学生比中间50%学生认为一致的OR值是1.328；年级的回归系数均无统计学意义（P＞0.05）。学校层面上，学校类别的回归系数无统计学意义（P＞0.05）。

表2 最终的两水平模型参数估计结果

关于是否认为本次考试试卷整体难度较大方面，性别、年级的回归系数差异没有统计学意义（P＞0.05）；学生成绩的回归系数差异有统计学意义，学生成绩百分等级处于上25%的学生和中间50%的学生比下25%学生认为试题难度大的OR值分别是0.302和0.558，上50%学生比中间50%学生认为试题难度大的 OR值是0.541（P＜0.05）；学校层面上，985/211院校比一般院校认为试卷“难度大”的 OR值是1.548，呈边际统计学意义（P＝0.053）。

对于是否认为使用临床场景的病例型试题考查基础医学知识增加试题难度，性别、年级的回归系数无统计学意义（P＞0.05）；学生成绩的回归系数有统计学意义，上25%学生和中间50%学生比下25%学生认为难度增大的 OR值分别是0.816和0.829（P＜0.05）；上25%学生比中间50%学生认为难度增大的OR值是0.984，但是差异无统计学意义（P＞0.05）。学校层面上，学校类别的回归系数无统计学意义（P＞0.05）。

讨 论

在拟合随机斜率模型的过程中，斜率的方差和协方差均为零，说明目前的数据不能很好估计解释变量的随机斜率，不适宜采用随机斜率模型，因此本研究的最终模型是随机截距模型。

本研究以实例采用两水平分层logistic模型分析的方法，探索了学生层面和学校层面不同特征对调查指标的影响。研究结果表明，调查指标回答的不同主要源于学校内部学生之间的差异，学校之间的差异较小。学生成绩对调查指标有正面影响。在控制其他变量的条件下，不同考试成绩的学生在所研究问题的回答上有显著差异，成绩越好的学生对考试越熟悉，对考试难度的感知上也觉得越容易，考查知识点与教学重点内容一致性的认知上也更高，越不认为采取情境型试题会增加试题难度。性别之间仅在考查知识点与教学重点内容一致性的问题上差异有统计学意义，其余三个问题差异均无统计学意义。年级之间相比，问题的回答没有差异。不同学校类别在四个调查指标的看法略有不同，但是差异较小，无实际意义。本次调查中不同学校类别之间表现出的差异可能与本次研究不同学校类型在组织动员学生参加考试的做法不同，有的学校有激励机制、在考前对学生进行充分的讲解动员有一定关系。

对大多数学生而言，学习态度与考试成绩之间有很强的相关关系［6］。学习态度越正确，考试成绩越高。考试之前，学生对考试的认知起主导作用，是增强其学习动机的来源之一。执业医师法正式实施后，考取执业医师资格证是医学生能否成为临床医师的门槛，给医学毕业生的顺利就业带来不小的压力，学生意识到执业医师资格考试对毕业后顺利就业的重要意义。本次考试属于医师资格考试实证研究的一部分，因此，在校本科生特别是临近毕业的学生对考试的形式、题型等有所了解。本研究中68%的4年级和5年级学生对考试内容熟悉，高年级学生面临毕业，因此对于考试更为熟悉，男生和女生之间的熟悉程度差异较小，没有统计学意义。本次问卷结果也印证了学生的学习态度与考试成绩相关的观点。

本次研究中大多数学生认为考试内容与教学内容一致。70%的学生认为本次考试考查的内容80%以上是教学中必须掌握的重点内容。学生对于试题和试卷难易度的认识上，性别之间和年级之间的差异较小，且差异无统计学意义。学生的能力水平与其对考试难度的态度有一定的关系，考试成绩较差的学生对试题和试卷难度持消极否定的态度。控制了其他因素后，相比一般院校，985/211院校的学生认为试卷的难度较大，原因可能是本次考试两类学校的学生在备考方面有区别。

对基础医学知识使用临床场景的病例型试题考查难度影响上，一般院校认为增加了试题难度，原因可能是我国大部分医学院是以基础课程和临床课程分离的教学方式为主，4年级和5年级主要是进行临床教学，那么这部分学生的基础医学部分的知识因为没有及时复习而有所遗忘，如果考前没有充分的准备，必然会感到难度大，而整合课程是近年来国内医学院校教学改革的热点方向，特别是985/211院校，在课程整合方面进行了积极探讨。中国医科大学乔敏等以实验研究法对整合课程的教学效果进行了研究，结果显示整合课程提高了学生分析问题和解决问题的能力，基础医学课程的整合有助于学生学习临床课程［7］。因此，985/211院校的学生对于基础知识在临床场景下的灵活运用有优势。

本研究虽然取得了一些有意义的结果，但也存在有待进一步改进的地方:首先，本研究以学生在某个时间点测得的成绩来考察对调查指标的影响，可能会影响学校变量对学生影响的估计；其次，由于学校的样本量较小，会导致统计效能减小，同时，学校一级变量的解释能力有限，可能与数据本身有关，今后的研究应从扩大样本量与增加多个时间点的测量、筛选学校层面的变量入手，追踪探讨学校变量的影响。

［1］Leeuw JD，Kreft I.Random coefficient models for multilevel analysis.Journal of Educational Statistics，1986，11:57-85.

［2］Snijders TAB，Bosker R.Multilevel Analysis:An Introduction to Basic and Advanced Multilevel Modeling.CA:Sage Publications，1999:20-62.

［3］王济川，谢海义，姜宝法，著.多层统计分析模型——方法与应用.高等教育出版社，2010.

［4］Rasbash J，Steele F，BrowneW，etal.A User′s Guide to MLwiN，v2.33.Centre for Multilevel Modelling，University of Bristol，2004.

［5］Barcikowski R.Statistical Power with Group Mean as the Unit of A-nalysis.Journal of Educational＆Behavioral Statistics，1980，6（6）:267-285.

［6］王振英.大学生考试态度研究.大家，2012:160.

［7］乔敏，张云，杨泽礼，等.基础医学整合课程教学效果的实验性研究.医学教育，2005（4）:26-29.

△通信作者:何佳

（责任编辑:郭海强）