变权组合模型在我国手足口病发病率预测中的应用*

华北理工大学公共卫生学院（063000） 王永斌 李向文 柴 峰 袁聚祥 尹素凤 武建辉

变权组合模型在我国手足口病发病率预测中的应用*

华北理工大学公共卫生学院（063000） 王永斌 李向文 柴 峰 袁聚祥△尹素凤 武建辉

目的探讨变权组合模型在我国手足口病月发病率预测中的应用，并与ARIMA模型和残差自回归模型的预测效果进行比较。方法收集2008年1月至2014年12月我国手足口病月发病率资料，用SPSS13.0和Eviews8.0拟合三种模型，并用2014年7－12月的数据比较三种模型的拟合和预测效果。结果ARIMA模型、残差自回归模型和变权组合模型拟合及预测的 MRD，MSE，RMSE和 MAE分别为 14.006，4.689，2.165，0.147和 13.565，4.416，2.101，0.133；16.793，7.247，2.692，0.171和 16.206，6.639，2.577，0.164；8.447，1.843，1.358，0.092和 8.409，1.833，1.354，0.082。结论变权组合模型拟合及预测效果优于ARIMA模型和残差自回归模型。

ARIMA模型 残差自回归模型 组合模型 手足口病 发病率 预测

手足口病（hand-foot-mouth disease，HFMD）是由多种人肠道病毒引起的一种儿童常见传染病，2008年卫生部列为丙类传染病，其常出现暴发或流行［1］。因此了解其流行规律及流行趋势，对于探索手足口病的病因线索和疾病预防策略及措施的制定具有至关重要的作用。由于手足口病发病常具有季节性特点，采用季节性自回归滑动平均混合模型（ARIMA）预测手足口病的发病是目前最常用的方法之一，但尚未见到基于ARIMA模型和残差自回归模型的变权组合模型在手足口病发病率预测中的应用。因此，本研究采用变权组合模型对我国2008年1月－2014年12月手足口病月发病率建立预测模型，对比其与ARIMA模型和残差自回归模型对手足口病月发病率预测的准确性，以探讨其在手足口病预测预警方面的可行性，从而为完善我国手足口病的监测和防制工作提供参考依据。

资料与方法

1.资料

资料来源于中国疾病预防控制中心传染病直报系统，人口资料来源于中国卫生统计局。具体计算的发病率见表1。

2.ARIMA模型［2－4］

（1）ARIMA模型预测分为3个阶段:识别、估计和诊断、预测应用。通过这3个处理步骤的反复进行，最终确定一个用于预报或控制的最优模型。（2）识别:利用相关的分析来确定序列的平稳性、随机性和季节性，并选定特定的模型来分析序列数据。（3）参数的估计和诊断:依据赤池信息准则（AIC）和Schwarz贝叶斯准则（SBC）确定模型阶数，建立ARIMA预测模型。在不断改变模型的阶数后，AIC与SBC值最小的模型为最佳模型。模型的诊断就是残差序列应是白噪声过程，并且参数均具有统计学意义。其自相关系数（ACF）和偏自相关系数（PACF）不应与0有显著的差异，且Box－LjungQ统计量应无统计学意义。模型公式如下:φ（B）Ф（Bs）▽d▽SDXt＝θ（B）Θ（Bs）εt；E（εt）＝0，var（εt）＝σ2，E（εtεs）＝0，s≠t E（xtεt）＝0，∨s＜t。公式中，B为后移算子，εt为残差，d和 D分别为非季节和季节差分次数，p和q分别为自回归和滑动平均阶数，P和Q分别为季节自回归和滑动平均阶数；▽d＝（1－B）d；▽DS＝（1－B）SD；φ（B）＝1－φ1B－…φpBp；θ（B）＝1－θ1B－…θqBq；Ф（Bs）＝1－Ф1Bs－…ФPBPs；Θ（Bs）＝1－Θ1Bs－…ΘQBQs。

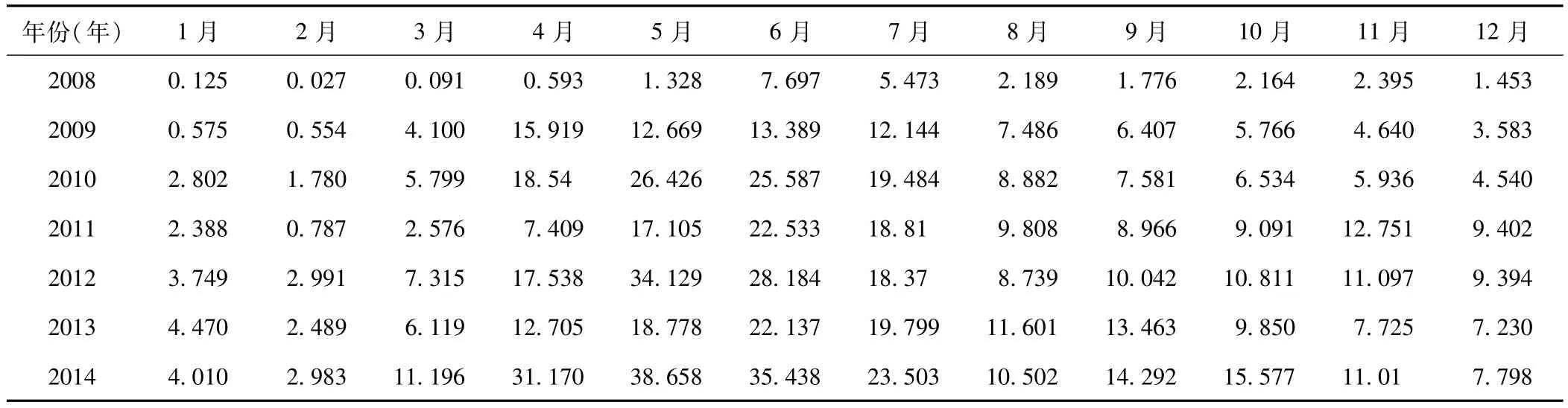
表1 2008年1月－2014年12月我国手足口病发病率（1/10万）

3.残差自回归模型［3－4］

残差自回归模型的结构为:Xt＝Tt＋St＋εt。其中，Tt为趋势效应拟合，St为季节效应拟合，εt为残差序列。常采用以自变量为历史观测值和以自变量为时间t的幂函数来拟合趋势效应。本研究中最终选用幂函数拟合趋势效应。对于季节效应的拟合常采用给定季节指数和对季节建立自回归模型的方法。本研究最终选用季节指数法，其步骤为:①用移动平均法消除季节性变动和不规则变动，得到循环性变动和长期趋势序列值；②利用序列的实际值除以相应的循环性变动和长期趋势序列值，然后用月平均法消除不规则变动，得到季节指数S'，若各季节指数的平均数不等于1时，需对季节指数进行修正处理，得到S＝（12/实际季节指数之和）×S′。

对残差序列采用DW法进行自相关性检验，DW值一般在2左右不存在自相关，那么不需要对残差提取二次信息；否则，应该对残差序列再次拟合，以提高模型拟合的精度。残差序列的自回归模型表达式为εt＝φ1εt－1＋φ2εt－2＋…＋φpεt－p＋at，并对残差序列的自回归模型进行检验和诊断。模型的残差序列应是白噪声过程，并且参数均应具有统计学意义。

4.变权组合模型［5］

以ARIMA模型和残差自回归模型的拟合值与实际值的误差平方和为依据，对单个预测模型的预测值赋予不同的权系数，用权系数乘以单个模型的预测值，然后相加即可得到变权组合模型的预测值；本研究中采用倒方差法确定权重，该方法是对误差平方和小的模型赋予大的权重，反之则赋予小的权重。计算如下:

对一时间序列有J种预测方法，x（t）为t时刻的实际值，＾x（jt）为第j个模型在t时刻的预测值，各个模型权重的计算公式如下:

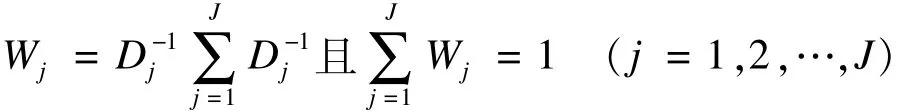
式中的Dj为第j个预测模型在t时刻的误差平方和

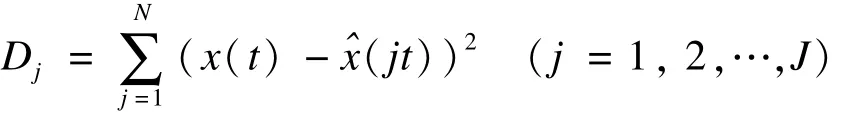
5.模型预测效果比较

基于2008年1月－2014年6月手足口病月发病率建立相关模型，用2014年7－12月数据进行外回代验证模型的外推预测效果，评价指标包括相对误差（RD），平均相对误差（MRD），均方误差（MSE），均方根误差（RMSE）和平均绝对误差（MAE）［6］。

6.统计学分析

运用 Excel2007建立数据库，用 SPSS13.0和Eviews8.0进行有关数据分析，检验水准α＝0.05。

结 果

1.ARIMA模型结果

利用Eviews8.0进行单位根检验，单位根统计量ADF＝-1.494952，P＝0.5306＞0.05，提示我国手足口病发病率序列为非平稳序列。所以首先进行对数转换和D＝1的季节差分。再结合经过对数转换和季节差分的ACF和PACF图，残差情况，以及系数之间的相关性选取AIC和SBC最小，对数似然函数值最大，且模型各参数均有统计学意义的模型为最优模型，通过比较，结合模型简洁的原则得到最优的模型是ARIMA（2，1，1）×（0，1，1）12，具体方程为（1－B）（1－B12）X t＝（1－0.637B）（1－0.448B12）εt/（1－0.891B＋0.501B2），其残差的ACF和PACF见图1，非季节性自回归系数 AR1＝0.891（t＝6.060，P＜0.001），AR2＝－0.501（t＝－4.626，P＜0.001），非季节性滑动平均系数 MA1＝0.637（t＝3.652，P＝0.001），季节性滑动平均系数 SMA1＝0.448（t＝3.492，P＝0.001），AIC＝64.078，SBC＝75.391，对数似然函数值为 －27.039。并且残差序列Box-LjungQ统计结果显示统计量差异均无统计学意义（P＞0.05），说明残差序列是白噪声。此模型的预测结果见表2。

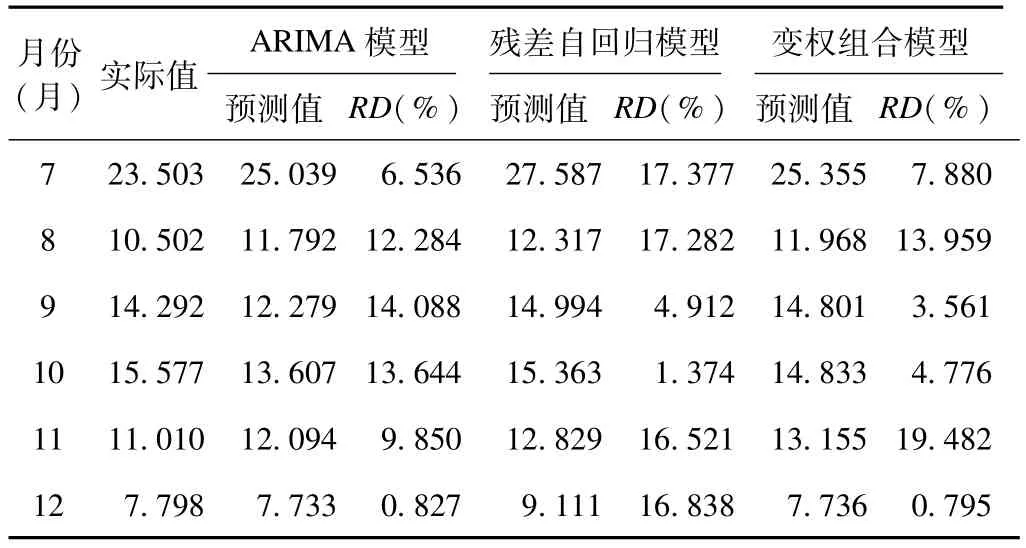
表2 2014年7－12月手足口病月发病率（1/10万）三种模型的预测外回代验证值

2.残差自回归模型结果

对原始数据分解出时间序列中的季节指数见表3。趋势效应的最佳拟合方程为Tt＝0.278×t0.967（t为序列号，R2＝0.806）。此即为确定性模型，对该模型的拟合效果进行DW检验，DW＝0.675，查DW检验临界值表，dL＝1.598，dU＝1.652，根据 DW→2时，DW＜dL时，序列显著正相关。提示残差序列高度正相关。因此，需要对残差序列进行自回归拟合。首先通过自相关图和偏自相关图（图1）确定自回归模型的阶数，残差的自相关图显示出典型的短期相关性，偏自相关图显示出典型的2阶截尾，所以对残差序列拟合AR（2）模型，非季节性自回归系数 AR1＝0.810（t＝7.452，P＜0.001），AR2＝－0.239（t＝－2.200，P＝0.031），具体表达式为 εt＝0.810εt－1－0.239εt－2＋at，对｛at｝残差序列采用DW法进行自相关性检验，DW＝1.958，非常接近2，所以｛at｝残差序列不存在自相关性了，并且残差序列Box－LjungQ统计结果显示统计量差异均无统计学意义（P＞0.05），说明残差序列是白噪声。最终的残差自回归模型为:

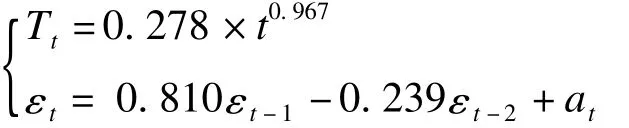
表3 手足口病发病率季节指数

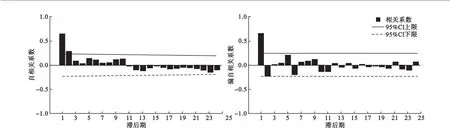
图1 残差序列的ACF和PACF图

计算出趋势效应方程和对残差建立的自回归方程的预测值，用预测值乘以相应的季节指数，得到最终的预测结果见表2。

3.变权组合型预测结果

根据公式计算的2014年7－12月ARIMA模型和残差自回归模型的误差平方和及权重见表4。变权组合模型的预测结果见表1。

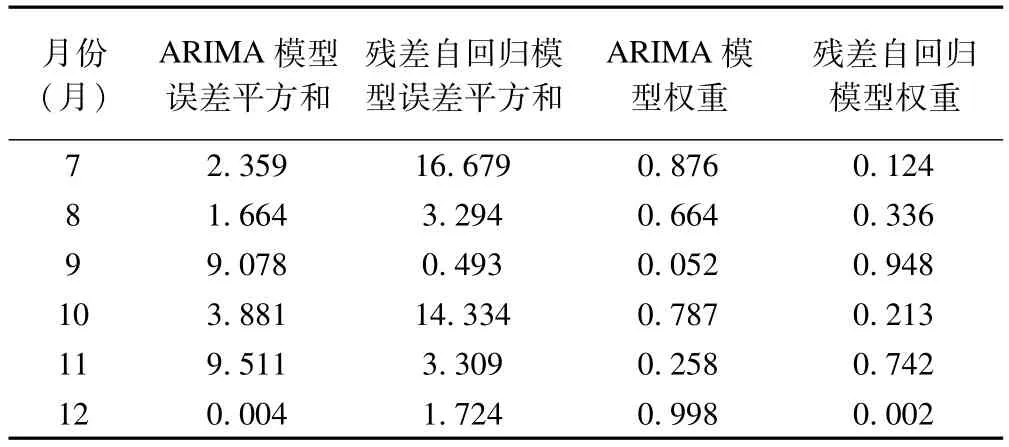
表4 2014年7－12月ARIMA和残差自回归模型的误差平方和及权重

4.三种模型预测效果比较

由表5可知变权组合模型拟合和预测性能均优于ARIMA模型和残差自回归模型。从图2可以看出变权组合模型拟合的曲线与实际值的曲线最接近。

讨 论

近年来预测的理论和应用得到了迅速的发展，并日趋完善。在医学和公共卫生领域，多种统计预测方法已被广泛应用于人口预测，疾病发病率，医院门诊量，药品需求的预测等领域中［7］。因此，如能找到合适的模型对传染病的发病率进行预测，将有助于卫生资源的合理配置，实现利益最大化，具有非常重要的现实意义［8］。由于传染病发病率数据一般均存在长期性变化、周期性变化和随机干扰。ARIMA模型预测时综合考虑了时间序列的各种影响因素（包括未知因素），从而提高了非平稳时间序列短期预测的拟合精 度［5］，已经被广泛应用于传染病发病率预测中。

表5 三种模型对手足口病月发病率的拟合及预测效果比较

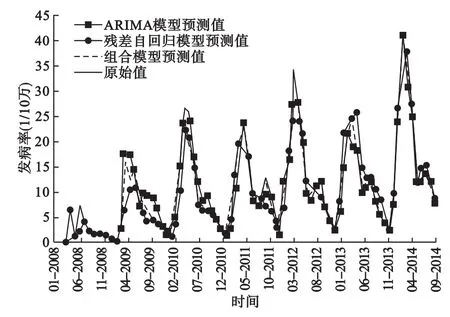
图2 三种模型对手足口病发病率拟合预测对比图

但ARIMA模型无法直观解释时间序列的动态特征及发展趋势。而其建模过程比较简单，适宜作为短期预测模型。残差自回归模型对具有显著的确定性趋势或季节趋势的时间序列数据，不但可以利用确定性分解法对序列的各种确定性效应进行解释，还可以对残差信息加以利用，所以兼有确定性因素分解法和ARIMA模型的优点［4］。而目前采用残差自回归模型预测手足口病的效果并不理想，因此为了探讨变权组合模型在预测手足口病发病率方面的可行性。本研究尝试将ARIMA模型和残差自回归使用变权的方式进行组合后预测手足口病发病序列，并与单一模型的预测效果进行比较。研究结果表明变权组合模型较好的拟合了手足口病的变化规律，显示了较高的预测精度，可以较好的在数理层面对手足口病发病率进行预测。相关报道［2，9］指出拟合及预测的MRD≤5%时为理想状态，但本研究中变权组合模型拟合及预测的MRD稍大，分别为8.447和8.409。因此，在预测手足口病发病率方面，更优的预测模型仍须进一步研究和验证。

本研究中尽管ARIMA模型和残差自回归模型拟合及预测精度低于变权组合模型，但模型拟合及预测的 MRD＜20%时为合格模型［2，9］，可以用于预测。就单一ARIMA模型和残差自回归模型拟合及预测的MRD来看，其仍然可以用于预测我国手足口病发病率。但值得注意的是:使用残差自回归模型对时间序列进行预测时，序列的样本点一般不能少于30个，当序列长度达不到要求时，只能使用确定性时间序列分析。

综上所述，尽管变权组合模型对我国手足口病发病率预测存在一定误差，但仍可对手足口病发病率进行早期预测、预警，为手足口病防控工作提供参考依据，从而减少或者消除决策的盲目性［7］。但需注意的是，在实际工作中，对季节性时间序列进行分析时，在满足模型使用条件的情况下，应将多种单一模型组合进行预测，选取拟合及预测误差都较小的组合模型对序列进行分析，并应不断收集新的时间序列数据，对已建立的模型进行验证。

［1］Zhang W，Huang B，She C，et al.An epidem ic analysis of hand，foot，and mouth disease in Zunyi，China between 2012 and 2014.Saudi Med J，2015，36（5）:593-598.

［2］王永斌，郑瑶，柴峰，等.基于周期分解的ARIMA模型在甲肝发病率预测中的应用.现代预防医学，2015，42（23）:4225-4229.

［3］Tarassenko L，Villarroel M，Guazzi A，et al.Non-contact video-based vital sign monitoring using ambient light and auto-regressive models.Physiol Meas，2014，35（5）:807-831.

［4］王燕主编.应用时间序列分析.第2版.北京:中国人民大学出版社，2005:87-172.

［5］毛瑛，井朋朋，吴静娴，等.我国卫生人力资源的组合预测模型构建及应用.中国卫生经济，2015，34（5）:21-24.

［6］戴钰.最优组合预测模型的构建及其应用研究.经济数学，2010，27（1）:92-98.

［7］刘桂芬主编.医学统计学.第2版.北京:中国协和医科大学出版社，2009:346-365.

［8］张国良，后永春，舒文.三种模型在肺结核发病预测中的应用.中国卫生统计，2013，30（4）:480-483.

［9］Liu L，Luan RS，Yin F，et al.Predicting the incidence of hand，foot and mouth disease in Sichuan province，China using the ARIMA model.Epidemiol Infect，2015，12（3）:1-8.

Application of the Weight Changeable Combination Model in Prediction on Incidence of HFMD in China

Wang Yongbin，Li Xiangwen，Chai Feng，et al.（School of Public Health，North China University of Science and Technology（063000），Tangshan）

ObjectiveTo explore the application of ARIMA model and auto-regressive model and weight changeable model in prediction on incidence of HFMD in China and compare the predictive effect among them.MethodsThe data of monthly incidence of HFMD from January 2008 to December 2014 in China was collected and Spss13.0 and Eviews 8.0 were used to fit three models.Afterwards，the data from July to December in 2014 was used to evaluate the predictive effect.ResultsThe MRD，MSE，RMSE and MAE fitted and predicted by ARIMA model and Auto-Regressive model and weight changeable model were 4.006，4.689，2.165，0.147 and 13.565，4.416，2.101，0.133；16.793，7.247，2.692，0.171 and 16.206，6.639，2.577，0.164；8.447，1.843，1.358，0.092 and 8.409，1.833，1.354，0.082，respectively.Conclusions According to the model fitness and prediction accuracy，the weight changeable model is superior to the ARIMA model and Auto-Regressive model with a good practical value.

ARIMA model；Auto-regressive model；Combination model；HFMD；Incidence；Prediction

河北省卫生厅医学科学研究重点课题计划（20130055）

△通信作者:袁聚祥，E-mail:yuanjx@heuu.edu.cn

（责任编辑:刘 壮）