基于蒙特卡洛RMT去噪法小股票组合风险优化研究

李冰娜，惠晓峰，李连江

1 东北大学秦皇岛分校 经济学院，河北 秦皇岛 066004 2 哈尔滨工业大学 管理学院，哈尔滨 150001 3 东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004

基于蒙特卡洛RMT去噪法小股票组合风险优化研究

李冰娜1，惠晓峰2，李连江3

1 东北大学秦皇岛分校 经济学院，河北 秦皇岛 066004 2 哈尔滨工业大学 管理学院，哈尔滨 150001 3 东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004

在Markowitz证券投资组合理论的框架下，证券收益协方差矩阵往往受到“维数灾祸”的影响而充斥噪声，这给Markowitz证券投资组合的构建及其风险的优化带来了严重的困扰。在对证券收益协方差矩阵去噪进而实现证券投资组合风险优化方面，基于随机矩阵理论(RMT)的去噪方法是一种非常具有优势的有效方法。

从说明Markowitz股票投资组合风险的含义入手，以投资组合风险预测的准确率衡量投资组合风险的优劣，继而对用于股票收益协方差矩阵的原有RMT去噪法的原理进行阐释。在此基础上分析认为小股票组合条件下原有RMT去噪法因噪声特征值边界界定误差而会产生组合风险优化作用下降的问题，为解决该问题，采用蒙特卡洛模拟法确定收益协方差矩阵的最大噪声特征值，从而建立蒙特卡洛RMT去噪法。对LCPB去噪法、PG+去噪法和KR去噪法等原有RMT去噪法和蒙特卡洛RMT去噪法的组合风险优化作用开展实证研究。

研究结果表明，各种RMT方法对相等加权协方差矩阵去噪前后的组合风险结果与指数加权协方差矩阵的组合风险结果非常类似；收益协方差矩阵未去噪时，随着股票数量减小，组合风险的优化水平越来越高，这主要是因为收益协方差矩阵噪声不断减小；当对收益协方差矩阵去噪时，随着股票数量的减小，原有RMT去噪法比蒙特卡洛RMT去噪法具有的去噪优势因原有方法对噪声特征值边界界定误差的增大而呈减小趋势，因此，组合中股票降至较低数量时，原有RMT去噪法的组合风险优化作用开始变得低于蒙特卡洛RMT去噪法，这说明蒙特卡洛RMT去噪法是一种解决小股票组合风险优化条件下原有RMT去噪法效力下降问题的有效方法。

新的蒙特卡洛RMT去噪法提供了证券投资组合权重分配的具体方法，提高了组合风险预测的准确率，对设计合理的证券投资策略和优化证券投资风险具有参考意义。

Markowitz投资组合；组合风险优化；小组合；RMT去噪法；蒙特卡洛模拟

1 引言

Markowitz投资组合理论表明对证券投资组合进行决策往往需要利用证券收益多元波动率(协方差矩阵)[1]。该矩阵一般只能由证券收益率的市场观测值来估计，但是实际观测值序列长度的有限(即所谓的“维数灾祸”)会使估计出的矩阵存在噪声，尤其是当证券数量较大时，估计噪声甚至会起主导作用[2]。不难想象，在此基础上测算的证券投资组合难免会对人们的投资决策造成误导，并且导致组合未来风险的预测也是不准确的。因此，对证券收益协方差矩阵(下文简写为协方差矩阵)去噪是实现证券投资组合风险优化的前提[3]。

近年来，源自于经济物理学的随机矩阵理论(random matrix theory, RMT)[4]的去噪法凭借其独特的优势在证券协方差矩阵去噪，进而实现证券投资组合风险优化方面发挥了巨大的作用[5]。然而，相对于几百只乃至上千只证券的组合而言，RMT去噪法对较小数量证券的组合，特别是百只以下证券组合的协方差矩阵去噪的作用很小，因此，对这些规模较小的组合风险优化效果很差。如何改进RMT去噪法对小股票组合协方差矩阵的去噪效力，以促进小股票组合风险的优化是值得密切关注的问题。在美国，大多数基金的投资组合囊括了超过100种证券，但个人投资者的投资组合规模一般都不大。与美国相比，中国证券投资组合的规模更小，主要原因是中国资本市场以中小投资者为主，机构投资者所占比例较低，且投资规模较小[6]。可见，现实经济生活中小规模投资组合的使用是非常多的。因此，研究解决小组合条件下RMT去噪法的误差问题，以期实现小股票组合风险的优化，对指导证券市场投资风险管理和满足日益增长的投资理财需求有重要的现实意义。

2 相关研究评述

学者们基于RMT对金融收益多元波动率[7]的噪声进行了大量研究，发现金融协方差矩阵的绝大部分特征值处于RMT预测的噪声带内，它们代表协方差矩阵中的噪声，而仅有个别特征值大于最大随机特征值，它们包含资产间相关的信息[8-9]。针对金融收益多元波动率中的噪声，LCPB去噪法、PG+去噪法和KR去噪法等传统RMT去噪法被相继提出，并在证券投资组合风险优化方面进行了大量的应用。也有个别学者对这几种方法进行了适当的变换，不过这方面的探索较少。

最先产生的RMT去噪法是LCPB去噪法，它是由LALOUX et al.[10]建立的，对该方法的实证结果表明去噪使组合风险预测误差大大降低；LEE[11]利用随机相关矩阵谱的中心极限定理识别出S&P 500的233只代表性股票在1997年1月2日至2001年5月11日的日收益相关矩阵的噪声带后，用LCPB去噪法对该矩阵进行了去噪。RMT去噪法在证券组合选择方面的作用明显优于其他方法。PAFKA et al.[12]使用模拟方法对比了样本相关矩阵、基于单一指数法的相关矩阵和基于RMT的相关矩阵用于证券组合选择的表现，结果显示，在减弱噪声影响方面，RMT去噪法的确是一种十分有效的降维方法；TOLA et al.[13]将聚类算法和RMT去噪法用于证券组合优化，并从可靠性、风险和有效资产数量3个方面对二者的效果进行比较，他们的结论是在理想化的条件下，即对未来收益和波动率有完全的预测能力和允许卖空时，聚类法的可靠性优于RMT方法，单一连接聚类法的风险水平高于平均连接聚类法和RMT去噪法，而它的有效资产数量明显低于后两种方法。

除LCPB去噪法外，PLEROU et al.[14]也提出了一种基于RMT的去噪法，即PG+去噪法。PG+法与LCPB法的原理非常相似，它们都对噪声特征值的替代进行简单、粗糙的处理。为实现RMT去噪法算法的改进，SHARIFI et al.[15]提出了基于RMT和协方差矩阵特征向量Krzanowski稳定性的KR去噪法。虽然KR去噪法具有非常明显的理论优势，但它在实际应用中的组合风险优化效果尚需进一步验证。对此，DALY et al.[16]使用LCPB去噪法、PG+去噪法和KR去噪法对资产数量为100、250和432的组合协方差进行去噪，发现KR法能最大程度地降低平均已实现风险。通过观测已实现风险评价组合风险优化效果的研究还有很多，如KAROUI[17]应用RMT方法研究Markowitz组合的已实现风险；RUBIO et al.[18]基于RMT研究高维样本下最小方差组合的已实现方差；WAKAI et al.[19]分析随机矩阵方法构建的均值-方差模型的最优组合的典型特点。除美国等发达国家证券市场外，一些学者基于RMT开展了发展中经济体证券市场特征谱的类似研究。TANG et al.[20]发现上海证券市场523只A股股票和深圳证券市场445只A股股票的收益相关矩阵存在大量噪声，基于RMT对它们去噪，结果表明去噪后构建的投资组合优于原始样本相关矩阵和Kendallτ相关矩阵建立的投资组合；OH et al.[21]基于RMT研究韩国证券市场上证券相关矩阵的统计特性及其对Markowitz组合权重的影响，发现由去噪前后相关矩阵计算得到的组合风险的熵函数是一个幂函数；韩华等[22]以上海证券市场数据为样本，基于RMT探讨金融相关矩阵特征值的统计特性，并对金融相关矩阵进行去噪，以使其更适合于构建金融网络。随着RMT在金融领域应用的不断深入，一些研究并非仅单独利用RMT方法，而是注重RMT方法与其他理论和方法的有机整合。ARAI et al.[23]将主成分分析与RMT结合起来，以东京股票交易所日收益数据为样本，运用所建立的复杂PCA方法分析股票收益相关矩阵，结果表明收益相关矩阵最大特征值表示一种对所有股票价格都会产生影响的市场力量，可以根据其他较大特征值对应的特征向量对股票进行分类；YANG et al.[24]应用RMT去噪法滤除证券相关矩阵中的噪声和共变趋势，继而用加权多目标遗传算法对证券进行分群；WANG et al.[25]基于RMT研究发现全球证券指数间相关可以由一个全球因素模型作出解释，他们进一步说明了该模型在降低全球范围内投资组合风险方面的价值；WANG et al.[26]使用皮尔森相关系数法和去趋势相关系数法构建S&P 500指数的462只成分股票间的相关矩阵，并采用RMT法分析它们的统计特性，结果表明去趋势相关矩阵的一些特点对最佳组合选择和风险管理很有帮助。

除将RMT用于资产数量较大的组合外，也有学者将其用于小证券组合的研究。CONLON et al.[27]采用LCPB去噪法对49个对冲基金105个月的月收益协方差矩阵进行去噪，并将去噪后的协方差矩阵用于构建组合基金，结果表明RMT去噪法对组合基金风险的改进作用较小；KUMAR et al.[28]利用RMT方法研究20个金融指数的相关和网络特性，发现第二大特征值对应特征向量的成分能够将各指数在正负方向上分为两类，这两类指数的成分值在金融危机期间会向相反方向转换。这些研究表明RMT去噪法用于小证券组合风险优化的效果非常不显著。事实上，也有一些研究认为，当将RMT去噪法应用于小证券组合时，甚至无法产生任何风险优化的作用。PAFKA et al.[29]采用RMT方法对指数加权协方差矩阵去噪，结果表明当组合中资产数量较小时，样本协方差矩阵的组合风险稍低于采用RMT法去噪的协方差矩阵；DALY et al.[30]还将LCPB法、PG+法和KR法用于39种外汇资产协方差矩阵的去噪，结果表明去噪效果随资产数量减少而下降；SANDOVAL et al.[31]发现用RMT方法去噪并不能产生更好的组合风险预测结果，而将RMT去噪法与消除市场效应的回归模型法结合起来却在62.5%的情况下能带来更好的风险预测结果。

与国外研究相比，中国学者基于RMT探讨金融市场中投资组合优化和风险管理问题的研究很少。罗英等[32]应用随机矩阵理论及方法解析中国股票组合协方差矩阵的信息结构，发现它存在受市场因素和行业因素主导的信息结构。韩华等[22]、唐晓清等[33]和惠晓峰等[34]在讨论股票协方差矩阵相关结构的基础上，进一步开展协方差矩阵去噪和投资组合构建的研究工作。韩华等[22]基于RMT对金融相关系数矩阵去噪，并构建了金融网络模型；唐晓清等[33]基于RMT改进了Markowitz组合投资模型, 结果表明RMT可以侦测到“异常” 数据, 从而改进对模型参数的估计；惠晓峰等[34]在Markowitz投资组合理论框架下研究RMT去噪法用于多元GARCH模型的有效性，结果表明RMT能够为多元GARCH的降维提供有效的依据，并且较准确地确定多元GARCH模型的最佳维度。

从上述研究看，原有RMT去噪法主要包括LCPB法、PG+法和KR法。从这些方法应用的对象看，它们不仅用于对上百只甚至几百只资产的大组合进行去噪，也用于百只以下资产的小组合；但与大组合的去噪效果相比，它们对小组合的去噪作用并不明显，有时甚至带来负的组合风险优化效果。已有研究基于小组合情形下协方差矩阵噪声较低的规律，将RMT去噪法对小组合作用的不明显化或“失灵”视为一种十分正常的现象，即这种现象的发生并不是由RMT去噪法自身的原因导致的。然而，对RMT去噪法的原理进行细致的分析发现，在小组合条件下原有RMT去噪法的算法都有比较严重的缺陷，即最大噪声特征值的解析解存在较大的计算误差，这难免会对组合风险优化带来负面影响。目前，从RMT去噪法自身存在问题的视角探讨它们对小证券组合风险优化作用降低的相关研究还比较少见。本研究正是从该角度展开研究，阐明Markowitz投资组合风险及其优化的有关基本概念，指出小组合风险优化时原有RMT去噪法的缺陷，即最大噪声特征值准确性下降的问题，并分析该问题产生的原因，提出蒙特卡洛RMT去噪法，最后进行以验证蒙特卡洛RMT去噪法效力为目的的实证研究工作。

3 Markowitz投资组合风险及其优化

Markowitz均值-方差模型的主要目的是通过对未来期的期望收益率和协方差矩阵的预测来对未来期的有效投资组合进行预测。在实际应用中，人们通常利用样本协方差矩阵对未来期的真实协方差矩阵进行预测。在此基础上根据Markowitz均值-方差模型构建的投资组合在本研究中称为Markowitz投资组合。为了表述方便，本研究将用于预测的历史数据所在的时期称为预测期，将发生投资的未来期称为投资期，Markowitz投资组合在投资期实现的风险称为Markowitz投资组合风险。

对Markowitz投资组合风险预测的准确性越高，则基于该预测做出的投资决策就越正确，投资组合给决策者带来的利益也就越大。因此，本研究用Markowitz投资组合风险预测的准确率表示Markowitz投资组合风险的优化水平。当对Markowitz投资组合风险的预测准确率提高时，则意味着Markowitz投资组合风险实现了优化。

4 小组合条件下原有RMT去噪法的缺陷

4.1 原有RMT去噪法的原理

到目前为止，还没有专门针对小组合而设计的RMT去噪法。与大组合相同，能够用于小组合协方差的RMT去噪法主要有LCPB法、PG+法和KR法3种，这3种方法对金融协方差矩阵的去噪原理类似，都是依据矩阵的特征分解去噪。

股票样本协方差矩阵的计算方法主要包括相等加权法和指数加权法。假定N个时间序列长度为T、样本方差为σ2的股票收益序列r1,t，r2,t，…，rN,t的相等加权样本协方差矩阵为Seq，指数加权样本协方差矩阵为Sex。以Seq和Sex的特征值作为主对角线元素的对角矩阵分别记为Deq和Dex，以各特征值对应的特征向量作为相应的列形成的矩阵分别为Eeq和Eex，则

(1)

(2)

Seq和Sex的噪声能够在它们的特征值中反映出来。Seq和Sex的一部分特征值能够反映真实的相关信息，但由于用于计算它们的时间序列长度往往是有限(非无穷)的，因此，Seq和Sex会受到随机因素的干扰而产生一些无法反映真实相关信息的噪声特征值。由于它们的噪声特征值具有随机性特征，因此，可以依据相应随机矩阵的特征值分布来确定这些噪声特征值的范围。

首先说明Seq的噪声特征值的识别。Seq对应的随机协方差矩阵为R，即

(3)

其中，A为一个N·T矩阵，其中元素是均值为0、方差为σ2的独立、相同分布的随机变量。由于用于计算R的随机序列的个数、长度和方差与用于计算Seq的时间序列相同，因此，可以依据R的特征值分布区间确定Seq的噪声特征值的范围。

(4)

其中，γ为衰减因子，k为其指数，xi,k、xj,k为均值为0、方差为σ2的正态分布的随机变量，i=1,2,…,N，j=1,2,…,N，k=0,1,…,∞。用于计算M的随机序列的个数和方差与计算Sex的股票收益序列的个数和方差对应相等，因此，可以依据M的特征值分布区间确定Sex的噪声特征值的范围。

接下来，用[λ-，λ+]表示R和M的特征值区间，则Seq和Sex的特征值中属于[λ-，λ+]的部分应被识别为噪声特征值。然而，由于小于λ-的特征值对应的特征向量并不稳定，因此，在应用RMT去噪法时，通常将不大于λ+的特征值都当做噪声特征值而对其进行替换。在替换噪声特征值时，LCPB法、PG+法和KR法的做法各不相同。由于λ+界定了噪声特征值的上限，因此，这里将λ+称为最大噪声特征值。由于大于λ+的特征值并不是由噪声产生的，因此让它们保持不变。设对Deq和Dex中的元素进行部分保持和部分替换后形成的矩阵分别为Deq-filtered和Dex-filtered，则对Seq和Sex去噪后的结果分别为

(5)

(6)

4.2 最大噪声特征值的计算误差

(7)

其中，Q为股票时间序列长度与股票数量之比。

(8)

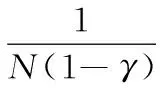
(9)

其中，v为函数F(v)取值为0时的解。

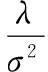
(10)

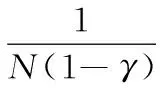
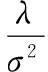
(11)

根据λ+的上述计算方法，原有RMT去噪法并没有真正计算λ+，而是用随机协方差矩阵在极限条件下的最大特征值近似地表示λ+。由于实际应用中N都是有限的，因此，原有RMT去噪法在N→∞时计算的λ+必然会偏离于真正的λ+。不难想象，两者的偏差会随N的减小而增大。当N较小时，对λ+的计算准确性也会因此降至较低水平。这种在小组合条件下对λ+的较大计算误差会造成噪声特征值的错误识别，并进一步对噪声特征值的替换造成不利的影响，导致发生替换过度或替换不足。无论是替换过度还是替换不足，都会令Deq-filtered和Dex-filtered无法被正确地确定，从而造成RMT方法去噪效力的下降，并进一步地对股票投资组合风险的优化带来不利的影响。尽管过去多年中RMT去噪法的应用较多，不过它们的上述误差问题却一直没有引起学者们的关注。

5 蒙特卡洛RMT去噪法的设计和实现

5.1 设计思想

为了消除小组合条件下RMT去噪法中λ+准确性下降的问题对投资组合风险优化的不利影响，本研究用蒙特卡洛模拟法确定λ+，从而设计了蒙特卡洛RMT去噪法，简称为MKR去噪法。除了λ+的确定方法外，蒙特卡洛RMT去噪法与原有RMT去噪法的原理相同。蒙特卡洛模拟方法的原理是：根据随机过程，用计算机模拟的方法生成时间序列，并将其作为抽样结果，以此计算参数估计值。蒙特卡洛模拟方法对参数的估计精度随模拟次数增多而逐渐提高，这保证了蒙特卡洛模拟法一般都能取得较高的估计精度。由λ+的原始计算模型可知，λ+的计算问题具有明显的概率特征，因此，蒙特卡洛模拟法非常适合于计算λ+。蒙特卡洛模拟法对相等加权协方差矩阵和指数加权协方差矩阵λ+的计算方法相同，因此，本研究以相等加权协方差矩阵为例介绍用蒙特卡洛模拟法确定λ+的原理。

5.2 蒙特卡洛模型构建

(12)

其中，

(13)

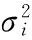
(14)

第1步 根据矩阵A概率模型中各行随机变量的分布，在计算机上产生随机数。每行产生符合概率模型的T个随机数，共产生N行，构成矩阵A的一次样本抽样。

第2步 应用A的一次样本抽样计算出矩阵R和它的全部特征值。设E为单位矩阵，那么|mE-R|=0中m的全部根就是R的全部特征值。设R的全部特征值为Rλ，Rλ={λ1,λ2,…,λN}，遍历所有特征值找到最大值λmax1。

第4步λmax的误差的计算公式为

ε=λασ

(15)

第5步 取得λ+的最终估计值。如果ε≤ε0，则第3步得到的λmax就是对λ+的最终估计值。否则，进行第101模拟，并计算λmax和其误差ε。若ε仍大于ε0，则继续进行第102次模拟。直至获得ε≤ε0时的λmax，该λmax就是对λ+的最终估计值。

从上面计算过程能够看出，蒙特卡洛RMT去噪法是用随机模拟法近似计算λ+的。由于它是在股票数量N取实际值的条件下计算λ+，因此能够有效解决对小组合去噪时原有RMT去噪法因限定N→∞的条件而引起对λ+计算准确性较低的问题，从而在组合资产数量较少时取得比原有RMT去噪法更好的去噪和组合风险优化效果。

6 基于蒙特卡洛RMT去噪法的小组合风险优化实证研究

6.1 研究方案设计

为验证蒙特卡洛RMT去噪法对原有RMT去噪法的改进作用仅适用于小组合的特点，本实证分析考察大小组合在内的不同股票数量下对组合风险预测的准确率。这样，当股票数量不断减小时，就可以对原有RMT去噪法和蒙特卡洛RMT去噪法的组合风险优化表现进行对比分析和趋势分析。具体地，组合内的股票数量N在[5,400]变化。协方差矩阵的计算采用日收益数据，所利用的原始股价数据来自wind数据库。将股价转换为收益率的方法为ri,t=lnpi,t-lnpi,t-1，pi,t为第i只股票在第t天的收盘价，ri,t为第i只股票在第t天的收益率，i=1, 2, …,N，t=1, 2, …,T。

图1 蒙特卡洛模拟流程Figure 1 Monte Carlo Simulation Process

图2 正态分布的累积分布函数Figure 2 Cumulative Distribution Function of Normal Distribution

步骤1 从2011年1月4日至2014年12月31日的所有日期中随机选择1个测试期。测试期后的1天为投资期，测试期前(包括测试期)的700天为预测期。

步骤2 从备选股票中随机选择N只股票。备选股票是在上海证券交易所上市交易且在该预测期和投资期内存在交易数据的全部股票。

步骤3 用预测期股票协方差矩阵对投资期协方差矩阵进行预测。当采用相等加权法时，预测期中第i只股票与第j只股票收益率的协方差为

(16)

其中，ri,t和rj,t分别为第i只股票和第j只股票第t天的收益率，t=1, 2, …, 700；〈·〉为700天的均值。当采用指数加权法时，预测期中第i只股票与第j只股票收益率的协方差为

(17)

步骤4 对于S的不同取值，计算对最小方差组合风险的预测准确率。根据S计算的最小方差组合中第i只股票的投资权重wi为[35]

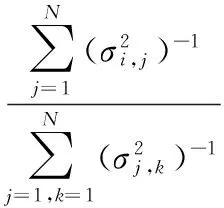
(18)

(19)

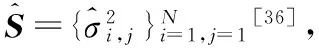
(20)

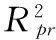
(21)

容易看出PR的值越接近于1，表示最小方差组合风险优化水平越高。

步骤5 在N不变的条件下重复20次步骤1～步骤4，然后分别计算10种协方差矩阵预测方法在20次试验中的平均PR。

步骤6 重复步骤1～步骤5，考察N不同时10种协方差矩阵预测方法的平均PR。

通过上述bootstrap方法，在T和γ不变的情况下得到相等加权协方差矩阵和指数加权协方差矩阵去噪前后的组合风险预测准确率随N的变化曲线，见图3和图4。

另外，为了给组合风险预测准确率分析提供更多论据支持，绘制N的不同取值下MKR去噪法基于蒙特卡洛模拟技术计算的λ+的模拟解和原有RMT去噪法计算的λ+的解析解的图形，见图5和图6。

6.2 实证结果和分析

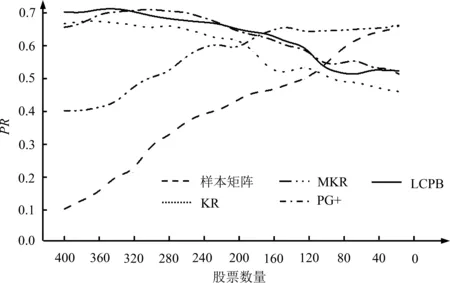
图3 相等加权协方差矩阵去噪前后的PRFigure 3 PR Pre- and Post- Filtering Equally Weighted Covariance Matrices

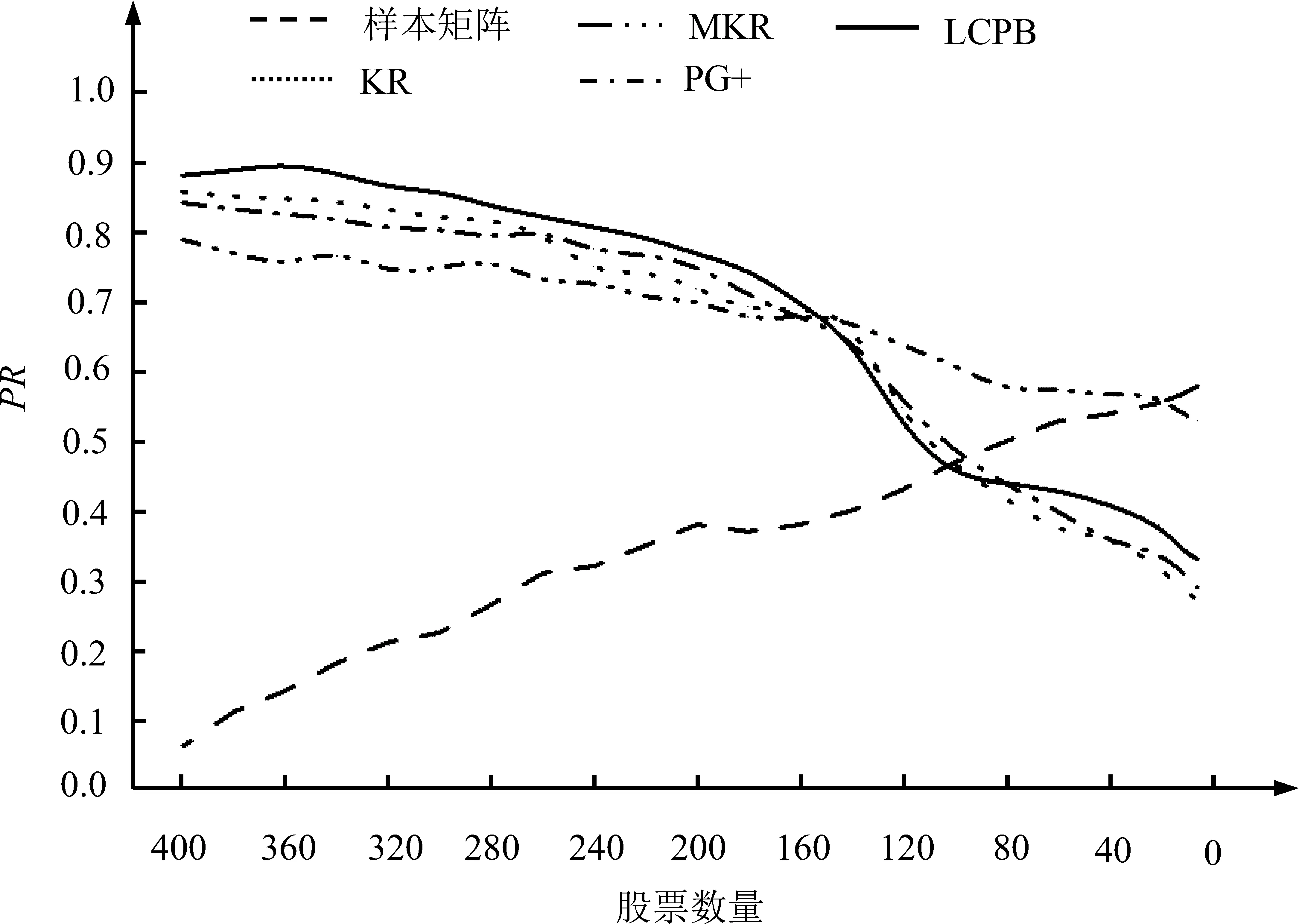
图4 指数加权协方差矩阵去噪前后的PRFigure 4 PR Pre- and Post- Filtering Exponentially Weighted Covariance Matrices

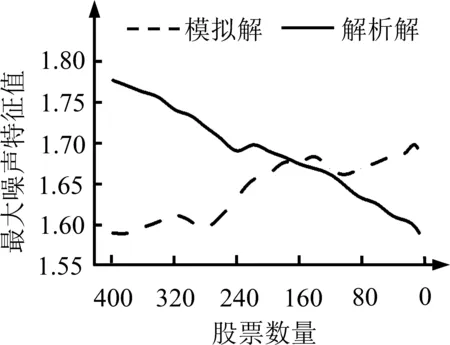
图5 相等加权协方差矩阵的最大噪声特征值Figure 5 The Maximum Noisy Eigenvalues of Equally Weighted Covariance Matrices

图6 指数加权协方差矩阵的最大噪声特征值Figure 6 The Maximum Noisy Eigenvalues of Exponentially Weighted Covariance Matrices

对各种去噪法的组合风险优化表现进行分析。如前所述，随着股票数量的减小，相等加权和指数加权协方差矩阵的噪声都越来越小，这必然导致PR受到的噪声影响越来越小，于是各种去噪法引起的PR的增加都呈现减小的趋势。由图3和图4可知，各种去噪法都能通过去噪而提高组合风险预测准确率，但它们对其改进的程度并不相同。

由于MKR去噪法是基于模拟技术计算λ+的，无法实现100%的精确度，所以MKR去噪法计算的λ+并非一种精确无误的解，且λ+的具体计算误差并不因N的改变而变化。根据4.2节的分析，LCPB法、PG+法和KR法等原有RMT去噪法对λ+的计算误差却随N的增大而减小。这导致当N足够大时，原有RMT去噪法对λ+计算的精确度高于MKR去噪法，且两者的差距呈现随N增大而扩大的趋势。如图5和图6所示，当N取最大值400时，原有RMT去噪法和MKR去噪法对λ+计算结果之差达到最大。在N逐渐减小的过程中，原有RMT去噪法和MKR去噪法对λ+计算差距出现减小的趋势，说明随着股票数量的减少，原有RMT去噪法对λ+计算的精确度不断下降，使原有RMT去噪法和MKR去噪法的去噪表现越来越接近。直至当股票数量减小到一定水平时，它们的去噪表现变得相同。对于相等加权协方差矩阵和指数加权协方差矩阵而言，原有RMT去噪法和MKR去噪法的去噪表现达到一致时的股票数量分别处于160～200和140～160的区间内。这与图5和图6的观察结果一致，由图5和图6可知，在相等加权法和指数加权法下，当N分别近似等于170和140时，原有RMT去噪法和MKR去噪法对λ+计算结果大致相等。在原有RMT去噪法和MKR去噪法的组合风险优化作用表现一致以后，当股票数量进一步减小，原有RMT去噪法引起的PR的增加开始变得低于MKR去噪法。此时原有RMT去噪法对噪声特征值的计算精度开始小于MKR去噪法，并且这种精度上的差距是随股票数量减小而不断增大的。λ+计算精度的上述变化特点可以由图5和图6直观地反映出来，由图5和图6可知，在原有RMT去噪法和MKR去噪法计算的λ+达到相同水平后，二者间出现了新的差距，即MKR去噪法计算的λ+的模拟解开始变得大于原有RMT去噪法计算的解析解，并且两者之差随N的减小而增大。这样，在各种去噪法引起的PR的增加都在随N不断减小而降低的过程中，由于原有RMT去噪法对λ+计算精度越来越小于MKR法，所以它们引起的PR的增加比MKR法先降到0，即不再具有去噪作用。由图3和图4可知，当采用相等加权法计算协方差矩阵时，PG+法、LCPB法和KR法的去噪能力降到0时的股票数量分别是91、98和110。对于指数加权协方差矩阵而言，PG+法、LCPB法和KR法的去噪效果达到0时的股票数量分别为93、107和100。之后，当股票数量进一步减小时，原有RMT去噪法无法起到去噪作用，反而造成PR的下降。而此时MKR法的去噪作用仍然存在。不过，类似于原有RMT去噪法，当股票数量减小至某一更低水平时，MKR法也会由于无法满足低噪声时的高精度要求而失去去噪能力。在相等加权法和指数加权法条件下，MKR法的去噪能力达到0时的股票数量分别为10和16。根据上面的分析，由于MKR法和原有RMT去噪法的差异主要体现在λ+的计算上，因此，股票数量较小时MKR法更好的去噪表现主要是由于λ+更高的计算精确度。

对相等加权协方差矩阵和指数加权协方差矩阵的PR进行比较分析。由图3和图4可知，在不同股票数量下，相等加权协方差矩阵去噪前的组合风险预测准确率都高于指数加权协方差矩阵去噪前的组合风险预测准确率。然而，相等加权协方差矩阵和指数加权协方差矩阵去噪后的结果却和去噪前的结果不同。当股票数量较大时，每一种去噪法对指数加权协方差矩阵去噪后的PR都高于对相等加权协方差矩阵去噪后的PR，而当股票数量降至接近100时，前者开始变得低于后者。如果将所有股票数量综合起来考虑，每一种去噪法对指数加权协方差矩阵去噪后的PR都大于对相等加权协方差矩阵去噪后的PR。根本来讲，这是因为每种去噪法引起的指数加权协方差矩阵的PR的增加都更大的缘故。

以上面分析为基础，对相等加权法和指数加权法下PR的最佳结果进行分析。由图3和图4可知，如果将两种协方差矩阵综合起来考虑，会发现PR的最高值因股票数量不同而变化。当股票数量较大时，LCPB去噪法对指数加权协方差矩阵去噪后的PR最高。当股票数量较小时，MKR去噪法对相等加权协方差矩阵去噪后的PR最高。而当MKR去噪法对相等加权协方差矩阵没有去噪能力时，相等加权协方差矩阵未去噪时的PR结果是最好的。

7 结论

本研究指出了小组合风险优化条件下对协方差矩阵去噪的原有RMT方法因噪声特征值边界界定误差而产生的去噪效力下降的问题，并为解决该问题，采用蒙特卡洛模拟法确定样本协方差矩阵的最大噪声特征值，从而建立了蒙特卡洛RMT去噪法。通过实证分析，在股票收益序列长度和衰减因子不变时，在不同股票数量下对LCPB法、PG+法和KR法等原有RMT方法和蒙特卡洛RMT法的组合风险优化效果进行对比研究，研究结果如下。

(1)实际应用中股票数量N是有限的，因此，原有RMT去噪法在N→∞时计算的λ+会偏离于真正的λ+。由于该误差随N的减小而增大，所以当对小组合去噪时，对λ+的计算误差会上升至较高水平，这必然造成小组合条件下原有RMT方法去噪效力的下降，并进一步对股票投资组合风险的优化带来不利的影响。

(2)各种RMT方法对相等加权协方差矩阵去噪前后的组合风险结果与指数加权协方差矩阵的组合风险结果非常类似。协方差矩阵未去噪时，随股票数量减小，组合风险预测的准确率越来越高，主要是因为股票数量的减小弱化了“维数灾祸”的作用，从而使协方差矩阵噪声减小。

(3)当股票数量足够大时，由于原有RMT去噪法对噪声特征值边界界定的精确度高于蒙特卡洛RMT去噪法，因此，原有RMT去噪法引起的组合风险优化水平的增加更大。随着股票数量的减小，相对于蒙特卡洛RMT去噪法，原有RMT去噪法的去噪优势因对噪声特征值边界界定误差的增大而呈减小趋势。直至当原有RMT去噪法的误差开始超过蒙特卡洛RMT去噪法的误差时，原有RMT去噪法的组合风险优化作用也开始变得低于蒙特卡洛RMT法。这说明蒙特卡洛RMT去噪法是一种解决小股票组合条件下原有RMT方法去噪效力下降的有效方法。

股票收益样本协方差矩阵含有的噪声会造成Markowitz股票投资组合风险优化水平的下降，而原有RMT去噪法在小组合条件下的效力却很小，甚至为0或负值。针对原有RMT去噪法的上述缺陷，本研究设计了蒙特卡洛RMT去噪法。本研究能够为证券市场投资中股票投资组合的权重分配提供具体的方法，对证券投资决策及有关政策制定均有一定的借鉴意义。由于本研究的实证研究仅以中国股票数据为样本，没有考虑其他国家，如一些发达经济体的证券市场情况，所以可能会影响实证结果的普适性，这是后续研究中需要进一步解决的问题。

[1]李洋,余丽霞.基于马科维茨理论的最优证券组合分析.财会月刊,2013(22):53-55.

LI Yang,YU Lixia.Analysis of optimal stock portfolio based on Markowitz theory.FinanceandAccountingMonthly,2013(22):53-55.(in Chinese)

[2]ZHANG M.Finite-sample linear filter optimization in wireless communications and financial systems.IEEETransactionsonSignalProcessing,2013,61(20):5014-5025.

[3]黄飞雪.基于单链接聚类过滤法的均值方差模型.预测,2011,30(1):66-70.

HUANG Feixue.Mean-variance based on filtered single linkage cluster.Forecasting,2011,30(1):66-70.(in Chinese)

[4]曾杏元.有关随机矩阵领域最新研究动态与进展的综述报告.数学理论与应用,2011,31(3):7-19.

ZENG Xingyuan.A survey on the latest dynamic and progress of random matrix field.MathematicalTheoryandApplications,2011,31(3):7-19.(in Chinese)

[5]CHU Chen,FANG Zhaoben.Optimal portfolio project with modified covariance matrix and its stability.JournalofUniversityofScienceandTechnologyofChina,2011,41(12):1035-1041.

[6]毛磊,王宗军,王玲玲.机构投资者持股偏好、筛选策略与企业社会绩效.管理科学,2012,25(3):21-33.

MAO Lei,WANG Zongjun,WANG Lingling.Institutional investors preferences,screening and corporate social performance.JournalofManagementScience,2012,25(3):21-33.(in Chinese)

[7]王明进.多元波动率模型的一些新进展.数理统计与管理,2010,29(2):232-247.

WANG Mingjin.Recent developments in multivariate volatility modeling.JournalofAppliedStatisticsandManagement,2010,29(2):232-247.(in Chinese)

[8]NGUYEN Q.One-factor model for the cross-correlation matrix in the Vietnamese stock market.PhysicaA:StatisticalMechanicsandItsApplications,2013,392(13):2915-2923.

[9]LIM K,KIM M J,KIM S,et al.Statistical properties of the stock and credit market:RMT and network topology.PhysicaA:StatisticalMechanicsandItsApplications,2014,407:66-75.

[10] LALOUX L,CIZEAU P,POTTERS M,et al.Random matrix theory and financial correlations.InternationalJournalofTheoreticalandAppliedFinance,2000,3(3):391-397.

[11] LEE Y H.Noisedetectionfromfinancialcorrelationmatrices.(2001-05-19)[2015-05-14].http:∥web.mit.edu/bazant/www/teach/18.325/projects.lee.ps.

[12] PAFKA S,KONDOR I.Estimated correlation matrices and portfolio optimization.PhysicaA:StatisticalMechanicsandItsApplications,2004,343:623-634.

[13] TOLA V,LILLO F.Cluster analysis for portfolio optimization.JournalofEconomicDynamics&Control,2008,32(1):235-258.

[14] PLEROU V,GOPIKRISHNAN P,ROSENOW B,et al.Random matrix approach to cross correlations in financial data.PhysicalReviewE,2002,65(6):066126-1-066126-18.

[15] SHARIFI S,CRANE M,SHAMAIE A,et al.Random matrix theory for portfolio optimization:a stability approach.PhysicaA:StatisticalMechanicsandItsApplications,2004,335(3/4):629-643.

[16] DALY J,CRANE M,RUSKIN H J.Random matrix theory filters in portfolio optimisation:a stability and risk assessment.PhysicaA:StatisticalMechanicsandItsApplications,2008,387(16/17):4248-4260.

[17] KAROUI N E.On the realized risk of high-dimensional Markowitz portfolios.SIAMJournalonFinancialMathematics,2013,4(1):737-783.

[18] RUBIO F,MESTRE X,PALOMAR D P.Performance analysis and optimal selection of large minimum variance portfolios under estimation risk.IEEEJournalofSelectedTopicsinSignalProcessing,2012,6(4):337-350.

[19] WAKAI R,SHINZATO T,SHIMAZAKI Y.Random matrix approach for portfolio optimization problem.JournalofJapanIndustrialManagementAssociation,2014,65(1):17-28.

[20] TANG L C,CHEN Y N.Noise dressing of ECM and investment portfolio selection based on RMT in China financial market∥ProceedingsofInternationalConferenceonManagement&ServiceScience.Piscataway:IEEE,2010:1-4.

[21] OH G,EOM C,WANG F,et al.Statistical properties of cross-correlation in the Korean stock market.TheEuropeanPhysicalJournalB,2011,79(1):55-60.

[22] 韩华,吴翎燕,宋宁宁.基于随机矩阵的金融网络模型.物理学报,2014,63(13):138901-1-138901-10.

HAN Hua,WU Lingyan,SONG Ningning.Financial networks model based on random matrix.ActaPhysicalSinica,2014,63(13): 138901-1-138901-10.(in Chinese)

[23] ARAI Y,YOSHIKAWA T,IYETOMI H.Complex principal component analysis of dynamic correlations in financial markets∥Proceedingsofthe5thKESInternationalConferenceonIntelligentDecisionTechnologies.IOS Press,2013:111-119.

[24] YANG J,WANG Z,LIU X,et al.Group identification in stock correlation networks with an application to portfolio selection.JournalofComputationalInformationSystems,2014,10(7):2937-2949.

[25] WANG D,PODOBNIK B,HORVATIC D,et al.Quantifying and modeling long-range cross correlations in multiple time series with applications to world stock indices.PhysicalReviewE,2011,83(4):046121-1-046121-9.

[26] WANG G J,XIE C,CHEN S,et al.Random matrix theory analysis of cross-correlations in the US stock market:evidence from Pearson′s correlation coefficient and detrended cross-correlation coefficient.PhysicaA:StatisticalMechanicsandItsApplications,2013,392(17): 3715-3730.

[27] CONLON T,RUSKIN H J,CRANE M.Random matrix theory and fund of funds portfolio optimisation.PhysicaA:StatisticalMechanicsandItsApplications,2007,382(2):565-576.

[28] KUMAR S,DEO N.Correlation and network analysis of global financial indices.PhysicalReviewE,2012,86(2):026101-1-026101-8.

[29] PAFKA S, POTTERS M,KONDOR I. Exponential weighting and random-matrix-theory-based denoising of financial covariance matrices for portfolio optimization.(2004-02-24)[2015-05-14].http:∥eprintweb.org/S/article/cond-mat/0402573/cited.

[30] DALY J,CRANE M,RUSKIN H J.Random matrix theory filters and currency portfolio opimisation.JournalofPhysics:ConferenceSeries,2010,221:1-14.

[31] SANDOVAL L,Jr,BORTOLUZZO A B,VENEZUELA M K.Not all that glitters is RMT in the forecasting of risk of portfolios in the Brazilian stock market.PhysicaA:StatisticalMechanicsandItsApplications,2014,410:94-109.

[32] 罗英,蔡玉梅,崔小梅,等.资产组合协方差矩阵的信息结构.预测,2013,32(4):26-30.

LUO Ying,CAI Yumei,CUI Xiaomei,et al.The information structure of the covariances between financial returns.Forecasting,2013,32(4):26-30.(in Chinese)

[33] 唐晓清,白延琴,刘念祖,等.基于随机矩阵理论的Markowitz组合投资模型.上海大学学报:自然科学版,2013,19(3):293-297.

TANG Xiaoqing,BAI Yanqin,LIU Nianzu,et al.Markowitz portfolio model based on random matrix theory.JournalofShanghaiUniversity:NaturalScience,2013,19(3):293-297.(in Chinese)

[34] 惠晓峰,李冰娜.基于随机矩阵理论决定多元GARCH模型最佳维度研究.运筹与管理,2011,20(4):141-148.

HUI Xiaofeng,LI Bingna.Study on determining the optimal dimension of multi-GARCH Models based on random matrix theory.OperationsResearchandManagementScience,2011,20(4):141-148.(in Chinese)

[35] CLARKE R,DESILVA H,THORLEY S.Minimum-variance portfolio composition.TheJournalofPortfolioManagement,2011,37(2):31-45.

[36] 瞿慧,刘烨.沪深300指数收益率及已实现波动联合建模研究.管理科学,2012,25(6):101-110.

QU Hui,LIU Ye.A joint model for CSI300 index return and realized volatility.JournalofManagementScience,2012,25(6):101-110.(in Chinese)

ResearchonRiskOptimizationofSmallStockPortfolioBasedontheFilteringMethodofRMTUsingMonteCarloSimulation

LI Bingna1，HUI Xiaofeng2，LI Lianjiang3

1 School of Economics, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China2 School of Management, Harbin Institute of Technology, Harbin 150001, China3 School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China

In the framework of classical Markowitz portfolio optimization problem, covariance matrices of stock returns obtained from historical data contain a high amount of noise, caused “curse of dimensions”, which will forbid the perfect construction of Markowitz portfolio and the optimization of its risk seriously. According to numerous studies, the filtering approaches based on random matrix theory are effective in reducing the estimation noise of financial covariance matrices and then achieving portfolio risk optimization.

Starting from the meaning of Markowitz stock portfolio risk, this work focuses on the accuracy of portfolio risk prediction as the measure for assessing optimal performance of portfolio risk and interprets the principle of the existing RMT-based filtering methods for stock return covariances. On this basis, we point out the calculation error of the maximum noisy eigenvalue in the existing RMT methods, which will turn out to reduce the ectiveness of these methods in the context of risk optimization of small portfolios. For any practical use of Markowitz portfolio theory, it would therefore be necessary to reduce this calculation error of the existing methods of RMT in the case of a small number of stocks. We introduce a new filtering method based on random matrix theory, which determines the theoretical edge of the random part of the eigenvalue distribution by a Monte Carlo simulation. Finally, we illustrate, on empirical data, the effect of the newly introduced method and the existing random-matrix-theory-based methods including LCPB, PG+ and KR on portfolio risk optimization.

Our empirical research has returned the following results. Firstly, whether covariance matrices of stock returns are filtered or unfiltered, it can be seen that, in general, the experimental results for equally weighted covariance matrices are very similar to those for exponentially weighted covariance matrices. Secondly, for unfiltered forecasts, the performance of portfolio risk is better when a smaller number of stocks is used for the estimation. The reason for this could be that the fewer stocks are used, the smaller amount of estimation noise can be in return covariance matrices. Thirdly, if enough stocks are taken into account, the existing RMT-based filters are superior to the newly proposed filter in terms of the risk optimization performance. However, the fewer the stocks are, the more inaccurately the maximum noisy eigenvalue in the existing filtering methods is calculated. As a consequence, the ectiveness of the existing filtering methods in the optimization of portfolio risk deteriorates as the portfolio size decreases. When the portfolio size is reduced to less than 200 stocks, the newly proposed filter begins to outperform the existing RMT filters. The results show that our novel filter is of great help in improving the ectiveness of the existing RMT-based filters in the context of risk optimization of small portfolios.

Combining the filtering procedure based on random matrix theory with the Monte Carlo simulation technique, the newly introduced filtering method can be very powerful in constructing portfolios with better weights allocation and improving the accuracy of portfolio risk prediction. In addition, our method also helps substantially in reasonable design of stock investment strategies and the optimization of stock investment risk.

Markowitz investment portfolio；portfolio risk optimization；small portfolio；RMT based filtering method；Monte Carlo simulation

Date:June 24th, 2015

DateMarch 4th, 2016

FundedProject:Supported by the National Natural Science Foundation of China(71401028), the Fundamental Research Funds for the Central Universities(N130323008) and the Funded by Northeastern University at Qinhuangdao(XNB201418)

Biography:LI Bingna, doctor in management, is a lecturer in the School of Economics at Northeastern University at Qinhuangdao. Her research interests include financial investment portfolio and risk management. Her representative paper titled “Optimization of stock portfolio risks based on correlation filtering using minimum perturbations of eigenvectors” was published inTheJournalofSystemsEngineering-theory&Practice(Issue 10, 2013). E-mail：libingna519@163.com

HUI Xiaofeng, doctor in management, is a professor in the School of Management at Harbin Institute of Technology. His research interests include exchange rate forecast, financial security and financial market efficiency. He is the principal researcher for the project titled “Disclosure of listed firms and capital costs” supported by the National Natural Science Foundation of China(70573030). E-mail：xfhui@hit.edu.cn

LI Lianjiang, doctor in engineering, is a lecturer in the School of Control Engineering at Northeastern University at Qinhuangdao. His research interests include multidisciplinary combined simulation. His representative paper titled “Research on improvement of ladar imaging quality based on fusion technology” was published in theLasersinEngineering(Issue 1-2, 2012). E-mail：lilianjiangpro@163.com

F830.91

A

10.3969/j.issn.1672-0334.2016.02.011

1672-0334(2016)02-0134-12

2015-06-24修返日期2016-03-04

国家自然科学基金(71401028)；中央高校基本科研业务费专项资金(N130323008)；东北大学秦皇岛分校校内基金(XNB201418)

李冰娜，管理学博士，东北大学秦皇岛分校经济学院讲师，研究方向为金融投资组合和风险管理等，代表性学术成果为“基于最小扰动相关去噪法股票投资组合风险优化”，发表在2013年第10期《系统工程理论与实践》，E-mail：libingna519@163.com

惠晓峰，管理学博士，哈尔滨工业大学管理学院教授，研究方向为汇率预测、金融安全和金融市场效率等，曾主持国家自然科学基金项目“上市公司信息披露与资本成本研究”(70573030)，E-mail：xfhui@hit.edu.cn

李连江，工学博士，东北大学秦皇岛分校控制工程学院讲师，研究方向为多学科联合仿真等，代表性学术成果为“Research on improvement of ladar imaging quality based on fusion technology”，发表在2012年第1-2期《Lasers in Engineering》，E-mail：lilianjiangpro@163.com