随机交易行为、羊群行为与资产价格波动研究

刘 刚，扈文秀，章伟果，贾丽娜

西安理工大学 经济与管理学院，西安 710054

随机交易行为、羊群行为与资产价格波动研究

刘 刚，扈文秀，章伟果，贾丽娜

西安理工大学 经济与管理学院，西安 710054

市场中交易者的随机交易行为与羊群行为和均值回归行为相互影响，并改变资产价格波动状态，但已有研究主要分析羊群行为和均值回归行为对资产价格波动的影响，对随机交易行为的研究较少。

基于行为金融理论，引入随机交易者，扩展已有的非线性资产价格动态波动模型，研究随机交易行为与羊群行为、均值回归行为的交互作用及其对资产价格波动的影响，剖析资产价格的形成路径，并构建模型，进而分析金融系统的均衡点特征和稳定性，最终利用MATLAB对资产价格波动进行数值模拟检验。

研究结果表明，市场中随机交易行为的存在导致资产价格不能收敛到资产的基本价值，只能收敛于偏离资产基本价值的一个均衡价格；当金融系统处于局部稳定状态时，均值回归交易程度与随机交易程度成正比，羊群行为的稳定范围与随机交易程度成正比、与均值回归交易程度成反比，且资产价格会以螺旋阻尼振荡走势收敛于资产的均衡价格；金融系统不处于局部稳定状态的两种状况，一是资产价格处于围绕资产均衡价格上下微幅周期震荡的稳定状态，二是资产价格波动幅度变大而处于的不稳定状态；随着市场中随机交易程度的逐步增大，资产均衡价格偏离其基本价值的幅度越大。

研究结果揭示了3种交易者行为与资产价格波动间的关系机理，完善了行为金融理论体系，并为政府部门稳定金融市场提出可供参考的建议，即培养交易者的价值投资理念，减少投机行为，防止信息不对称导致的羊群行为。

资产价格波动；随机交易行为；羊群行为；均值回归行为；金融系统；局部稳定

1 引言

中国近几年出现的房地产热、股票热等资产价格泡沫现象，使人们逐步认识到资产价格的剧烈波动会给整个经济发展带来巨大的安全隐患，因此，维护金融系统稳定越来越重要。资产价格的波动和金融系统的稳定受到市场预期的影响，市场预期又取决于市场中交易者的交易策略选择，已有研究主要从市场中的羊群行为、均值回归行为等方面剖析资产价格波动和金融系统的稳定性，而交易者行为中的随机交易行为常常被忽略，缺乏一般性。因此，研究市场中交易者的随机交易行为，不仅能更好地揭示资产价格波动的动态演化机理，而且能解释金融系统稳定的一些基本情况。

2 相关研究评述

2.1 非线性资产价格波动模型

MARKOWITZ[1]从资产收益和风险视角剖析不确定性条件下最优投资组合问题，他提出的投资组合理论(modern portfolio theory,MPT)为现代金融理论发展奠定了基础；SHARPE[2]利用构建的单因素模型提出证券投资组合的分析方法；LINTNER[3]和MOSSIN[4]在同一时期也构建了与SHARPE[2]基本一致的模型，其在假定投资者完全理性且预期一致、市场非常完善等基础上，分别提出资产定价模型(capital asset pricing model,CAPM)。但是由于CAPM模型在理论上的局限性，MERTON[5]首先将CAPM模型扩展为跨期资本资产定价模型(intertemporal capital asset pricing model, ICAPM)，而BLACK et al.[6]提出期权定价理论(option pricing model, OPM)，ROSS[7]进一步构建套利定价模型(arbitrage pricing theory,APT)，在此基础上，FAMA et al.[8]构建三因子模型(Fama-French 3-factor model,FF3)，一直到LUX[9]构建异质主体模型(heterogeneous agent model,HAM)。这一系列研究使资本资产定价模型从一个简单金融模型发展为具有深刻经济含义的理论，并且这些研究将自身纳入到一般均衡的分析框架下，使其能够在一定程度上解释资本市场上出现的有悖于标准金融理论中投资者异常交易行为和金融市场的各类异象。可以看出，虽然资产定价取得了丰硕的研究成果，但仍然不能较好地描述和刻画市场的实际情况，需要根据资本市场实际进一步剖析金融异象和资产价格异常波动情况。

为了分析资产价格波动的实际情况，结合国内外金融理论发展状况，本部分主要梳理了异质主体模型的发展。LUX[9]通过建立市场中投资者观念转换和传染的模型，剖析投资者受资产本身的信息及市场中其他投资者行为影响，导致资产价格围绕其基本价值波动，甚至存在资产价格泡沫的成分；KAIZOJI[10]认为交易者行为间的互相传染将会给金融市场带来泡沫；FORONI et al.[11]也认为股票市场中的传染效应会导致股票价格波动过于剧烈，可能会给股票市场带来毁灭性的冲击；HOMMES[12]总结了上述异质主体模型的发展；SCHMITT et al.[13]通过建立基于代理的包括异质投机者和基本面分析者的金融市场模型，解释国际股票市场中的泡沫及崩溃、厚尾分布、波动集群、持续成交量等一些重要的统计特征。综上可知，异质主体模型中将交易者主要分为基本面分析者和图表分析者，两类交易者将资产价格推向不同的方向(价格上涨、下跌)，他们之间的博弈导致资产价格不断波动而形成最终价格。中国学者结合中国金融市场发展，袁晨等[14]在研究中推广了异质主体模型，构建二维离散非线性资产价格动态模型，分析价值投资者的均值回归策略及图表者的传染效应，仿真模拟检验不同利率水平下价格的动态演化过程；并利用中国股票市场的数据进行检验，得出央行在加息、降息情形下股票市场的波动情况。在袁晨等[14]的研究基础上，刘祥东等[15]结合实验经济学相关理论，进一步推动异质主体模型的发展，通过数值模拟发现投资者的传染效应处于中等状态时，资产的价格能迅速收敛于资产基本价值，并分析资产结构与股价波动之间的关系。聂慧丽等[16]、张宗新等[17]和李合龙等[18]也实证检验了投资者预期与资产价格波动的关系。可以看出，异质主体模型同样适用于中国金融市场，但是还需要进一步深入分析投资者行为与资产价格波动的关系，从而能够剖析资产价格波动的本质。

2.2 投资者行为与资产价格波动

投资者的投资行为是指受宏观经济环境、需求与供给以及投资者自身的影响，在一定动机的驱动下为达到既定目标而做出的一些具体投资活动。国内外学者在研究投资者行为与资产价格波动的关系时，一般从理论分析、实证检验和实验模拟等方面展开。在理论分析方面主要通过构建模型剖析市场中的投资者行为，BIKHCHANDANI et al.[19]利用信息流模型解释市场中局部投资行为的一致性和集体投资行为的脆弱性，认为投资者容易做出跟随前面决策者的交易行为(即羊群行为)；AVERY et al.[20]通过分析基于不完全信息的羊群行为模型，发现由于股票价值和信息精度的不确定性，在极端的情况下可能导致股市泡沫和崩盘。在实证方面主要检验投资者羊群行为和均值回归交易行为两类交易行为，涉及到基金和股票市场等。SCHARFSTEIN et al.[21]剖析基金经理的集聚行为，认为基金经理存在模仿他人决策的交易行为，会导致股票价格产生异常波动；NAKAGAWA et al.[22]实证检验日本借贷市场中羊群行为对经济的影响；KAIZOJI et al.[23]发现20世纪末网络股泡沫时期的动量交易策略属于羊群行为；GALARIOTIS et al.[24]对比分析美国和英国股票市场中的羊群行为。通过这些实证检验可以发现，在金融市场中确实存在羊群行为，这类行为能够刺激资产价格发生剧烈波动。在均值回归交易行为方面，袁晨等[14]分析价值投资者的均值回归策略，并利用中国股票市场的数据进行检验，得出央行在加息、降息情形下股票市场的波动情况。在随机交易行为方面，STEFAN et al.[25]从模仿、不模仿、不关心3个方面的投资者行为构建基于做市商的模型，结果表明实际的股票市场指数是可以进行复制模拟的，其波动强烈影响市场的网络形态，其中不关心态度的投资者做出的投资行为会对市场产生随机的影响，此类交易者行为也称作随机交易行为。除了分析基金经理等个体羊群行为在市场中的作用，也有部分学者剖析机构羊群行为，许年行等[26]以中国A股上市公司和机构投资者持股数据为研究样本，发现机构投资者的羊群行为增加了股票价格在未来崩盘的风险；程天笑等[27]通过扩展和比较羊群行为的SAIS测度和FHW测度，发现中国境内机构投资者是市场波动的“领头羊”，QFII仅处于“从羊”的地位。但是，在机构投资者是否能够防止资产价格剧烈波动方面还存在相反的结论，LAKONISHOK et al.[28]认为机构投资者的分析能力较强，他们的羊群行为可以抵消中小投资者的非理性交易行为，进而促使资产价格波动处在合理的范围内。在分析基金市场中的投资者行为时，WERMERS[29]采用1975年至1994年美国股市的所有共同基金的样本数据，发现基金共同买入股票比共同卖出股票具有较高的同期滞后收益，进而得出基金管理者预期公司前景的羊群行为能够加速股票价格对信息的吸收，从而稳定市场。可以看出，虽然关于羊群行为是否能够引起资产价格发生剧烈波动的研究还没有形成统一结论，但是主流研究已经将资产市场中的羊群行为作为影响资产价格波动的一个重要因素。

除了在股票市场中检验投资者行为与资产价格波动的关系，部分学者借鉴实验金融的相关理论分析了二者之间的关系。陈莹等[30]利用计算金融实验分析得出羊群行为对股票价格波动有显著影响，并存在明显的协同羊群行为所引发的股票价格泡沫或崩溃。除市场中羊群行为对资产价格波动产生影响外，投资者情绪也是近年来研究资产价格波动的热点，而且投资者情绪本身也会影响到投资者行为。胡昌生等[31]从投资者情绪、文凤华等[32]从投资者积极情绪和消极情绪、YANG et al.[33-34]从投资者情绪和信息、YANG et al.[35]从投资者情绪和高预期、YANG et al.[36-37]从投资者情绪和投资者行为构建情绪资产定价模型，并结合中国上市公司数据建立投资者情绪模型，进而从投资者情绪角度实证检验投资者行为与资产价格波动间的关系。同时，也有学者通过数值模拟检验分析羊群行为与资产价格波动的关系，刘祥东等[38]根据金融市场稳定与否对羊群行为程度进行界定，通过数值模拟分别得出轻度、中度、重度羊群效应区间内股票价格的波动，与实际市场更加切合。此外，投资者行为的研究也得到进一步拓展，REKIK et al.[39]基于agent的仿真系统建模，对价值投资者、羊群行为者、风险厌恶者3类投资者进行人工股票市场建模，进而从行为视角研究市场的动态性，并利用投资者的非理性行为解释各类金融异常现象。可以看出，国内外学者从实证检验、实验模拟、数值模拟等方面分析投资者行为与资产价格波动的关系，并且对市场中的投资者行为进一步拓展，更加符合实际的资本市场情况。

总之，国内外学者对于资产价格波动的研究主要集中在非线性资产价格波动模型、投资者行为与价格波动关系分析方面，得到丰硕的研究成果。然而已有研究存在3个方面不足。①国内外学者主要从羊群行为交易者和均值回归交易者两类交易者情形下构建非线性资产价格波动模型，而没有将市场中的随机交易行为纳入分析框架中，缺失一般性；②已有研究利用实证、实验等方法对市场中的羊群行为、均值回归交易行为进行检验，分析羊群行为、均值回归交易行为对资产价格波动的影响，忽视了市场中随机交易行为对资产价格波动的影响；③国内外学者在分析资产价格波动时，一般假定资产价格会围绕资产基本价值波动，而没有考虑到资产价格受市场中交易者投资决策的影响，可能会发生资产均衡价格对资产基本价值的偏离。

基于此，本研究引入随机交易行为，剖析投资者行为相互作用下的资产价格形成路径，构建非线性资产价格动态波动模型；剖析资产价格均衡点特征，并进一步分析模型的稳定性；借鉴动态随机模拟仿真的实验经济学思想，利用MATLAB软件模拟资产价格动态波动过程，从而揭示随机交易行为、羊群行为、均值回归行为及其交互作用对资产价格波动的影响机理和效应。

3 非线性资产价格动态波动模型

3.1 基本假设及说明

3.1.1 资产

假设金融市场中只有一种资产，资产的价格随着市场中交易者整体预期的变动而变化。

3.1.2 随机交易行为、羊群行为、均值回归交易行为3类交易行为

(1)随机交易行为

借鉴STEFAN et al.[25]的研究成果，将随机交易行为定义为对资产价格进行判断时，交易者没有掌握资产的全部信息，包括共有信息和私有信息，并且也不关注这些信息，他们的交易策略对市场的整体预期会造成随机的上下波动，进而导致资产价格处于持续的波动状态，本研究界定采取此类交易行为的交易者为随机交易者。考虑到20世纪60年代初期，经济学家开始利用计算机分析时间序列数据，KENDALL et al.[40]在研究股票价格是否能够反映公司的前景时，发现没有任何可预测范式能够揭示股价的形成，股票历史数据不能预测股价的变化趋势，其价格变化是随机的。因此，在股票价格服从随机波动的思想基础上，结合股价变化的随机性，本研究探索性地以资产价格变化作为随机交易者进行投资决策的参照对象。

(2)羊群行为

借鉴BIKHCHANDANI et al.[19]的研究成果，将羊群行为定义为在市场信息不对称的情况下，交易者不能对资产基本价值进行判断，并且忽略自身拥有的私有信息，其交易决策受到市场整体投资态度的影响，进而模仿他人行动的决策。本研究界定采取此类交易行为的交易者为羊群行为交易者，并在后续的研究中以市场整体的平均预期作为羊群行为交易者进行投资决策的参照对象。

(3)均值回归交易行为

借鉴HOMMES[12]的研究成果，将均值回归交易行为定义为对市场中的信息进行全面收集，并做出合理分析，若当前资产价格低于基本价值时，主要采取投资的策略，直至资产价格恢复到基本价值时将资产出售，赚取资本利得；若当前资产价格高于基本价值时，主要采取出售资产或者选择不进入该市场的策略。本研究界定采取此类交易行为的交易者为均值回归交易者，并在后续的研究中以资产基本价值作为均值回归交易者进行投资决策的参照对象。

3.2 资产价格形成路径分析

交易者结合市场中当期资产价格的相关信息，采用随机交易行为、羊群行为、均值回归交易行为3种不同的交易行为，形成市场中买卖者转化概率，进而影响到交易者对下期资产价格的预期，最终形成下期的资产价格，并进一步影响市场中交易者的投资，从而形成资产价格产生的闭合回路，具体见图1。

由图1可知，资产价格由随机交易行为、羊群行为、均值回归交易行为3条路径共同作用形成。

(1)随机交易行为路径：②→④→⑤→⑥→②

节点④受节点②的影响形成节点⑤，而节点⑤影响节点⑥的形成，节点⑥对节点②的作用不明显，若市场中所有的交易主体都采用随机交易策略，那么资产价格会呈现无规则的波动，市场是失效的。

(2)羊群行为路径：③→④→⑤→③

节点④受节点③的影响形成节点⑤，而节点⑤最终作用到节点③，形成一个正反馈的闭合回路，若市场中所有的交易主体都采用羊群行为策略，那么资产价格将处于发散状态，不能收敛于基本价值，市场是失效的。

(3)均值回归交易行为路径：①→④→⑤→⑥→①

节点④受节点①的影响形成节点⑤，而节点⑤影响节点⑥的形成，节点⑥最终作用到节点①，形成一个正反馈的闭合回路，若市场中所有的交易主体都采用均值回归策略，那么资产价格会收敛于基本价值，市场是完全有效的。

3.3 模型构建

记n+、n-分别为买者和卖者的数量，市场中的交易者n=n++n-，每个交易者做出买或卖的决定，则交易者对资产价格未来的预期可以表示为

(1)

交易者在市场中会不断的对资产进行交易，每个交易者的投资态度也会发生相应的改变，假设t至(t+1)期间，交易者只作一次修改，记Pr+-为买者向卖者转变的概率，Pr-+为卖者向买者转变的概率。那么，在t至(t+1)期间，买者的净增长数量为n-Pr-+-n+Pr+-，卖者的净增长数量为n+Pr+--n-Pr-+，n-Pr-+为卖者转换到买者的数量，n+Pr+-为买者转换到卖者的数量。可以得出t至(t+1)期，市场整体对资产价格预期的变动量可以表示为

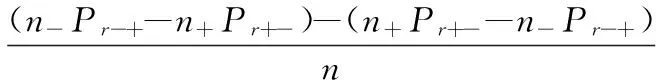
(2)

进一步计算可得

图1 资产价格形成路径Figure 1 The Path of Asset Price Formation

Xt+1-Xt=(1-Xt)Pr-+-(1+Xt)Pr+-

(3)

结合LUX[9]、KAIZOJI[10]和FORONI et al.[11]构建转换概率的思想，市场中交易者的随机交易行为、羊群行为、均值回归交易行为都在一定程度上受到资产价格的直接或间接影响，且相互影响，共同作用于交易者买卖观点的转变。借鉴STEFAN et al.[25]和KENDALL et al.[40]的研究成果，利用资产价格的随机变动性，以资产价格作为替代变量，衡量随机交易者的投资策略对买卖观点转换的影响；借鉴BIKHCHANDANI et al.[19]的研究成果，利用市场中交易者对资产价格未来的预期，以市场平均预期作为替代变量，衡量羊群行为交易者的投资策略对买卖观点转换的影响；借鉴HOMMES[12]的研究成果，利用资产基本价值与资产价格的偏离，以资产基本价值-资产价格作为替代变量，衡量均值回归交易者的投资策略对买卖观点转换的影响。因此，本研究定义的交易者买卖转换概率表达式为

(4)

(5)

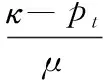
将(4)式和(5)式代入(3)式，得到(t+1)期市场整体对资产价格预期的动态表达式，即

(6)

为了分析资产价格的形成过程，借鉴DAY et al.[41]的研究成果，假设在市场中只存在一个做市商，且其根据超额需求来调整资产价格，若超额需求为正，资产价格上升；若超额需求为零，资产价格不变；若超额需求为负，资产价格下降。可见，做市商的存在可以保障资产价格随时变化，并维持资产供求平衡。资产价格的形成受市场超额需求的影响，而市场中交易者平均预期可以在一定程度上反映市场超额需求。用ξXt+1表示(t+1)期每个交易者对资产价格的平均预期，进而得出资产价格的动态关系式，即

pt+1=pt+f(ξXt+1)

(7)

其中，f(·)为非线性单调递增函数，f(0)=0；f(ξXt+1)为ξXt+1的价格调整函数。借鉴FORONI et al.[11]的相关研究，本研究最终选取f(ξXt+1)=λarctan(ξXt+1)，λ为交易者对资产价格预期的固定调整尺度，λ>0。得到资产价格调整表达式为

pt+1=pt+λarctan(ξXt+1)

(8)

由(6)式和(8)式可得出描述市场整体对资产价格的预期和资产价格动态变化的复杂金融系统，即

(9)

在上述金融系统中，若将随机交易者对资产价格的反应程度β设置为0时，此复杂金融系统回归到了原来的模型，与FORONI et al.[11]和刘祥东等[38]的模型和研究结论一致，说明扩展的模型确实有效。可以看出，本研究分析得出的金融系统，探索性的将随机交易行为纳入模型中，更接近市场的真实反应。

4 金融系统均衡点特征和稳定性分析

4.1 金融系统均衡点特征

假设M*为金融系统(9)式的均衡点，M*=(X*,p*)，X*为市场整体预期，p*为资产的均衡价格，均衡点M*=(X*,p*)满足

(10)

通过求解(10)式，可以得出

(11)

由于雅可比矩阵可以体现一个可微方程和已知点的最优线性逼近。因此，本研究借鉴雅克比矩阵的这个特性计算出金融系统的局部稳定条件，在均衡点M*=(X*,p*)处，用Jb表示金融系统(9)式的雅可比矩阵，即

(12)

(13)

对(13)式进一步简化，可得

(14)

不等式组(14)式是金融系统局部稳定的充分条件，进一步分析随机交易行为、羊群行为和均值回归行为在金融系统局部稳定时的关系，具体见图2(a)～图2(c)。

(a)随机交易行为与均值回归交易行为的关系

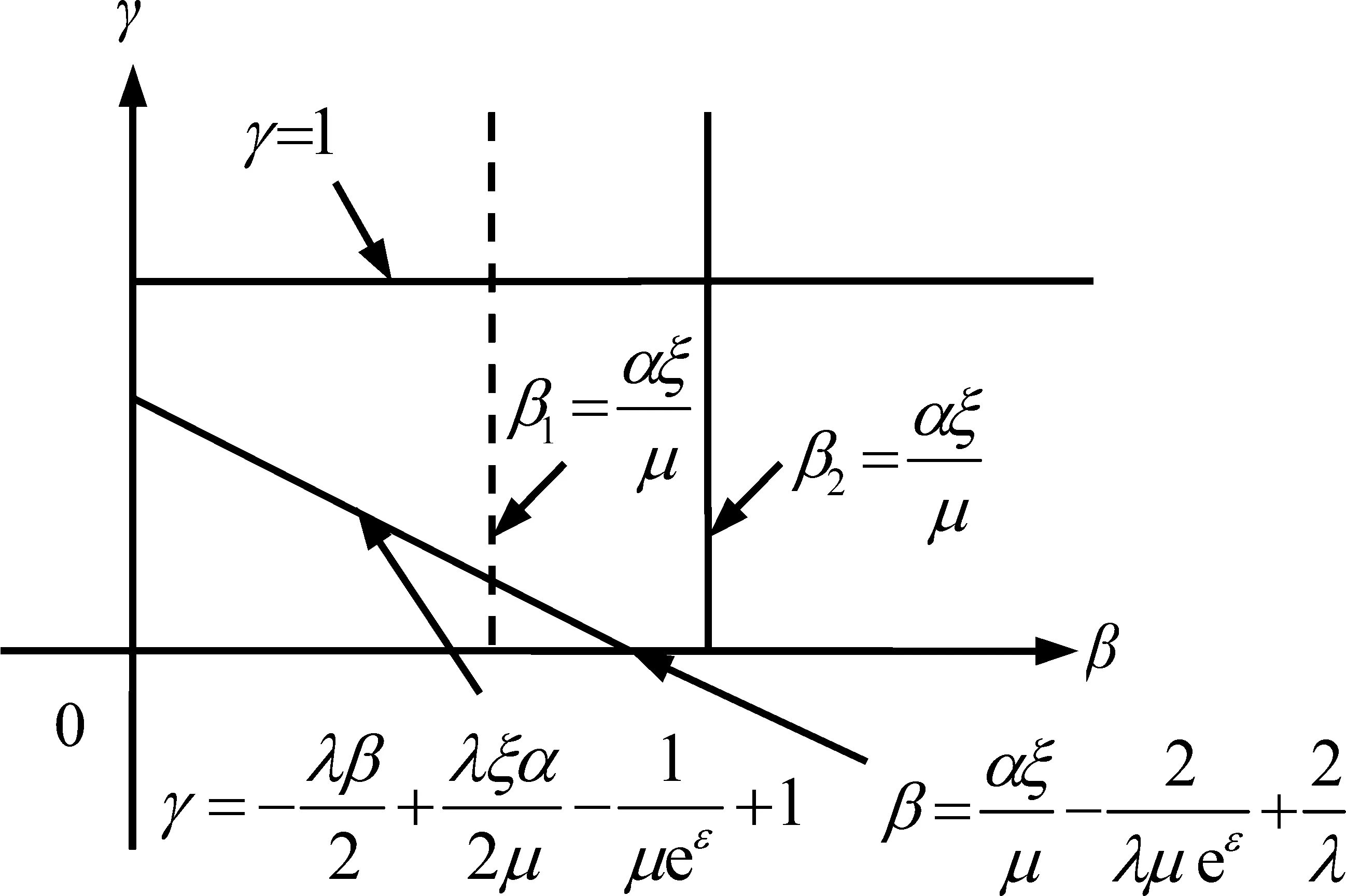
(b)随机交易行为与羊群行为的关系

(c)均值回归交易行为与羊群行为的关系

4.2 金融系统稳定性分析

(15)

其中，N=(2γ+λβ-2)eε。可以看出N为γ的单调递增函数，能够代替γ反映羊群行为程度。对金融系统稳定域的分析见图3。当N<0、λξαeε-2>0时，不等式组不成立，对于这种情况的一种解释是：当均值回归行为交易程度、交易者对资产价格预期的调整尺度很大，羊群行为程度、随机交易行为程度很小时，资产价格一旦偏离基本价值，市场就会将这种偏差进行纠正；当N>0、λξαeε-2<0时，不等式组不成立，对于这种情况的一种解释是：当均值回归交易行为程度、交易者对资产价格预期的调整尺度很小，羊群行为程度、随机交易行为程度很大时，资产价格将一直偏离基本价值，市场中的资产价格偏差不能得到有效的纠正。当N<0、λξαeε-2<0时，由μ1曲线、N轴、μ轴围成的区域为稳定域；当N>0、λξαeε-2>0时，由μ2曲线右边与N=λβeε围成的区域为稳定域。

图3 金融系统稳定域Figure 3 Stability Region of Financial System

若给定的参数在稳定域之内，那么由于资产价格受均值回归者的均值回归交易行为、随机交易者的随机交易行为和羊群交易者的羊群交易行为3类决策相互作用的影响，资产价格不能收敛到资产的基本价值，但是会逐步靠拢资产的均衡价格，对不等式组(15)式进行求解，得出随机交易行为、羊群行为、均值回归交易行为的区间表达式为

(16)

5 数值模拟

5.1 随机交易行为、羊群行为与资产价格波动分析

图4 当γ=0.75、 β1=0和β2=0.10时资产价格波动Figure 4 Whenγ=0.75、 β1=0 and β2=0.10, Asset Price Fluctuation

图5 当γ=0.30、 β1=0和β2=0.10时资产价格波动Figure 5 Whenγ=0.30、 β1=0 and β2=0.10, Asset Price Fluctuation

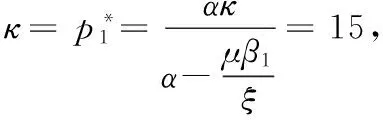
通过分析图4～图6可知，与FORONI et al.[11]和刘祥东等[38]的研究成果不同的是，由于受随机交易行为的影响，资产价格不能收敛到资产的基本价值κ，而只能收敛到资产的均衡价格p*。同时，不同羊群行为程度下的资产价格波动各不相同，在市场稳定的必要条件(0.496<γ<1、0.476<γ<1)情形下，资产价格以螺旋阻尼振荡走势收敛于均衡价格；在羊群行为程度较弱(γ<0.496、γ<0.476)情形下，资产价格围绕资产均衡价格持续性周期震荡；在羊群行为程度较强(γ>1)情形下，资产价格剧烈波动。在前两种情况下，资产价格在收敛于均衡价格或者资产价格在合理区间内波动，此时的市场是有效的；在第3种情况下，资产价格剧烈波动，超出资产价格波动的合理区间，此时的市场效率是低下的。

图6 当γ=1.10、 β1=0和β2=0.10时资产价格波动Figure 6 When γ=1.10、 β1=0 and β2=0.10, Asset Price Fluctuation

图7描绘了由于受到市场中随机交易行为、羊群行为、均值回归交易行为的影响，资产价格波动状态发生的相应的变化。首先是资产价格波动幅度不断变小，金融系统逐步稳定(其中：A点是整个金融系统稳定的最优点)；其次，资产价格波动幅度逐渐加大，金融系统逐渐由稳定状态趋向不稳定状态；最后，当资产价格波动幅度过大时(超过一定的限度时)，将有可能导致资产价格泡沫的产生，此时的金融系统处于不稳定状态，且资产价格中有泡沫的成分，本研究在此不做重点研究。

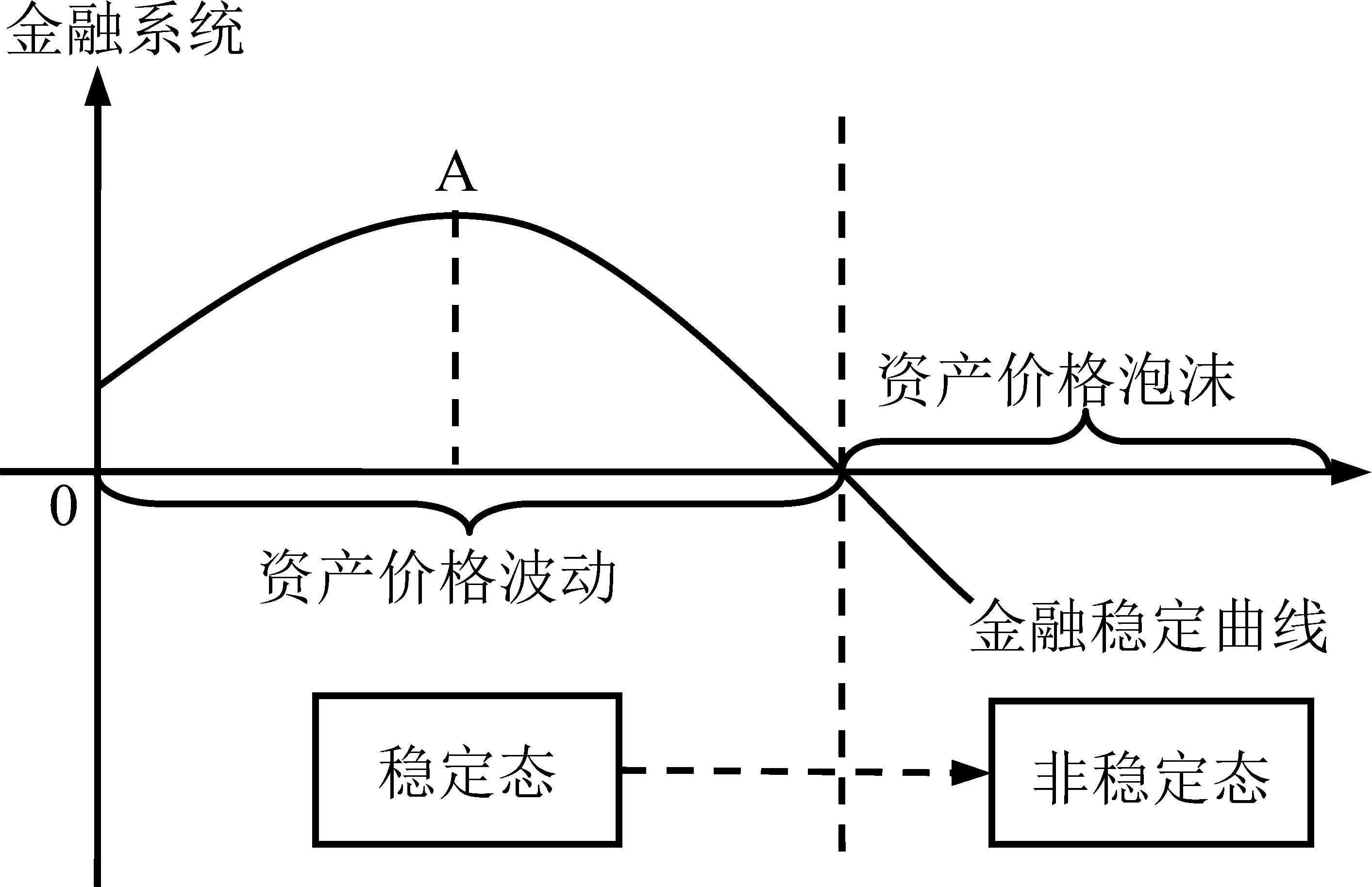
图7 金融系统稳定性Figure 7 Stability of Financial System

5.2 随机交易与资产均衡价格分析

结合FORONI et al.[11]和刘祥东等[38]的研究成果，本部分对各参数的设置情况为：μ=0.30，α=0.40，κ=15，ε=0.05，λ=0.40，ξ=10。为了方便研究，选取处于金融系统稳定域的羊群行为程度γ=0.75，研究随机交易行为对资产均衡价格的影响，进而选取随机交易程度β1=0.10、β2=0.20、β3=0.30分别进行模拟，具体见图8。

图8 随机交易行为与资产均衡价格Figure 8 Random Trading Behavior and Asset Equilibrium Price

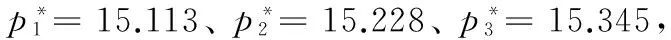
从理论模型推导和数值模拟检验结果进行分析，图9描绘了金融系统处于稳定状态时，市场中的随机交易行为、羊群行为、均值回归交易行为的关系。3种交易行为相互影响，共同作用于资产价格，可以得到：①随机交易行为导致资产价格处于不断的波动状态，羊群行为导致资产价格脱离资产的基本价值，均值回归交易行为导致资产价格收敛于资产的基本价值，最终3类交易行为相互博弈形成资产价格。②随着随机交易程度的逐步增大，资产均衡价格逐渐偏离资产的基本价值。

图9 随机交易行为与资产基本价值、资产均衡价格Figure 9 Relationship between Random Trading Behavior and Fundamental Value, Equilibrium Price of Asset

6 结论

基于行为金融理论，以交易者行为和资产价格波动为研究对象，通过引入一直被国内外学者和实业家忽略的随机交易行为，构建一个基于交易者行为的非线性资产价格动态模型，在分析金融系统均衡点特征及其稳定性的基础上，利用MATLAB软件对非线性资产价格的动态演化过程进行模拟。研究结果表明，①受随机交易行为、羊群行为、均值回归交易行为相互作用形成资产的价格，而市场中的随机交易行为导致资产价格不能收敛到资产的基本价值，只能收敛于资产的均衡价格。②金融系统处于局部稳定状态时，均值回归交易行为程度与随机交易行为程度成正比，羊群行为程度的取值范围随着随机交易行为程度的增大而逐渐扩大、随均值回归交易行为程度的增大而逐渐缩小；并且资产价格会以螺旋阻尼振荡走势收敛于资产的均衡价格。③金融系统不处于局部稳定状态分为两种情况：一种是资产价格处于围绕资产均衡价格上下微幅周期震荡的稳定状态；另一种是资产价格脱离资产均衡价格的幅度更大，资产价格波动更加剧烈的不稳定状态。④随着市场中随机交易程度的逐步增大，资产价格收敛到资产均衡价格的时间更长，并且资产均衡价格越来越脱离资产的基本价值。

市场中的随机交易行为导致资产价格不能收敛到资产基本价值，阻碍了金融系统的稳定，通过数值模拟检验也证实投资者行为确实能够影响资产价格波动，因此，如何通过影响投资者行为促使中国金融系统稳定已然成为政府部门必须考虑的问题。结合上面的研究过程和结果，为政府部门稳定金融系统提出如下建议。

(1)加强交易者投资理念的教育。投资理念的教育是一项系统工程，需要政府、教育部门、媒体等长期共同努力。一方面，为市场交易者普及各类基本投资理论和常用投资分析方法(如基本价值、技术分析、价值投资等)，引导市场交易者结合自身风险承受能力，选择相应的投资品种(如风险承受能力低，可以选择银行定期、债券等投资产品；风险承受能力高，可以选择基金、股票、股指期货等投资产品)，而不是凭借自己兴趣爱好选择投资品种形成随机交易行为；另一方面，教育投资者了解投资和投机的区别，减少投机交易者幻想通过赌博性投机在市场中获取超额利润。同时，媒体需要正确引导舆论导向，充分揭示市场中可能存在的风险，大力宣传各类投资工具、风险特征、交易流程、法律法规等。

(2)防止信息不对称导致的羊群行为。根据FAMA的“有效市场假说”，投资者无法获得超额收益，虽然完全有效的市场是不存在的，但是政府应该主张市场开放透明、信息公开，尽可能保证市场中所有参与者获得比较完全的信息。否则，在信息不对称情形下，一些利好因素会引导市场中交易者竞相进入该类资产，进而存在部分投资者盲目跟风产生羊群行为、追涨杀跌(如股票的暴涨暴跌等)，扰乱有效资产价格的形成。

可以看出，本研究对中国金融市场的稳定发展具有一定的借鉴意义，但是由于市场本身复杂多样，还存在一些局限。①本研究假设将市场中的交易主体分为三类，与实际市场中的交易者类型还存在一定的差距，后续研究将在此基础上进一步分析。②本研究过程中发现市场中的随机交易行为、羊群行为引发资产价格剧烈波动，可能导致资产价格泡沫的产生，后续将深入剖析可能存在的泡沫现象。③目前关于随机交易行为在市场中的测度指标还没有明确，故本研究只是通过数值模拟对资产价格波动过程进行检验，今后会结合金融市场实际数据深入剖析交易者行为与资产价格波动的关系。

[1]MARKOWITZ H.Portfolio selection.TheJournalofFinance,1952,7(1):77-91.

[2]SHARPE W F.Capital asset prices:a theory of market equilibrium under conditions of risk.TheJournalofFinance,1964,19(3):425-442.

[3]LINTNER J.The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets.TheReviewofEconomicsandStatistics,1965,47(1):13-37.

[4]MOSSIN J.Equilibrium in a capital asset market.Econometrica,1966,34(4):768-783.

[5]MERTON R.An intertemporal capital asset pricing model.Econometrica,1973,41(5):867-887.

[6]BLACK F,SCHOLES M.The pricing of options and corporate liabilities.JournalofPoliticalEconomy,1973,81(3):637-654.

[7]ROSS S A.The arbitrage theory of capital asset pricing.JournalofEconomicTheory,1976,13(3):341-360.

[8]FAMA E F,FRENCH K R.Common risk factors in the returns on stocks and bonds.JournalofFinancialEconomics,1993,33(1):3-56.

[9]LUX T.Herd behaviour,bubbles and crashes.TheEconomicJournal,1995,105(431):881-896.

[10] KAIZOJI T.Speculative bubbles and crashes in stock markets:an interacting-agent model of speculative activity.PhysicaA:StatisticalMechanicsandItsApplications,2000,287(3/4):493-506.

[11] FORONI I,AGLIARI A.Complex price dynamics in a financial market with imitation.ComputationalEconomics,2008,32(1/2):21-36.

[12] HOMMES C H. Heterogeneous agent models in economics and finance∥HandbookofComputationalEconomics.Amsterdam:North-Holland,2006:1109-1186.

[13] SCHMITT N,WESTERHOFF F.Speculative behavior and the dynamics of interacting stock markets.JournalofEconomicDynamicsandControl,2014,45:262-288.

[14] 袁晨,傅强.异质价格预期、无风险利率调整与证券市场波动.管理科学学报,2012,15(8):84-96.

YUAN Chen,FU Qiang.Heterogeneous price expectations,risk free rate adjustment and volatility of security markets.JournalofManagementSciencesinChina,2012,15(8):84-96.(in Chinese)

[15] 刘祥东,刘澄,王立民.资产结构与证券价格的非线性动态模型.中国管理科学,2012,20(6):9-17.

LIU Xiangdong,LIU Cheng,WANG Limin.Nonlinear dynamic model of capital structure and security price.ChineseJournalofManagementScience,2012,20(6):9-17.(in Chinese)

[16] 聂慧丽,张荣武,徐文仲.异质预期、群体演化与资产价格波动机制.会计研究,2012(7):65-71.

NIE Huili,ZHANG Rongwu,XU Wenzhong.Heterogeneous expectation,group evolution,and mechanism of asset price volatility.AccountingResearch,2012(7):65-71.(in Chinese)

[17] 张宗新,王海亮.投资者情绪、主观信念调整与市场波动.金融研究,2013(4):142-155.

ZHANG Zongxin,WANG Hailiang.Investor sentiment,subjective belief adjustment and market fluctuations.JournalofFinancialResearch,2013(4):142-155.(in Chinese)

[18] 李合龙,冯春娥.基于EEMD的投资者情绪与股指波动的关系研究.系统工程理论与实践,2014,34(10):2495-2503.

LI Helong,FENG Chun′e.Relationship between investor sentiment and stock indices fluctuation based on EEMD.SystemsEngineering-Theory&Practice,2014,34(10):4295-2503.(in Chinese)

[19] BIKHCHANDANI S,HIRSHLEIFER D,WELCH I.A theory of fads,fashion,custom,and cultural change as informational cascades.JournalofPoliticalEconomy,1992,100(5):992-1026.

[20] AVERY C,ZEMSKY P.Multidimensional uncertainty and herd behavior in financial markets.TheAmericanEconomicReview,1998,88(4):724-748.

[21] SCHARFSTEIN D S,STEIN J C.Herd behavior and investment.TheAmericanEconomicReview,1990,80(3):465-479.

[22] NAKAGAWA R, OIWA H,TAKEDA F.The economic impact of herd behavior in the Japanese loan market.Pacific-BasinFinanceJournal,2012,20(4):600-613.

[23] KAIZOJI T,LEISS M,SAICHEV A,et al.Super-exponential endogenous bubbles in an equilibrium model of fundamentalist and chartist traders.JournalofEconomicBehavior&Organization,2015,112:289-310.

[24] GALARIOTIS E C,RONG W,SPYROU S I.Herding on fundamental information:a comparative study.JournalofBanking&Finance,2015,50:589-598.

[25] STEFAN F M,ATMAN A P F.Is there any connection between the network morphology and the fluctuations of the stock market index?.PhysicaA:StatisticalMechanicsandItsApplications,2015,419:630-641.

[26] 许年行,于上尧,伊志宏.机构投资者羊群行为与股价崩盘风险.管理世界,2013(7):31-43.

XU Nianxing,YU Shangyao,YI Zhihong.Institutional investor herding and stock price crash risk.ManagementWorld,2013(7):31-43.(in Chinese)

[27] 程天笑,刘莉亚,关益众.QFII与境内机构投资者羊群行为的实证研究.管理科学,2014,27(4):110-122.

CHENG Tianxiao,LIU Liya,GUAN Yizhong.The empirical research of herding behavior between QFII and domestic institutional investors.JournalofManagementScience,2014,27(4):110-122.(in Chinese)

[28] LAKONISHOK J,SHLEIFER A,VISHNY R W.The impact of institutional trading on stock prices.JournalofFinancialEconomics,1992,32(1):23-43.

[29] WERMERS R.Mutual fund herding and the impact on stock prices.TheJournalofFinance,1999,54(2):581-622.

[30] 陈莹,袁建辉,李心丹,等.基于计算实验的协同羊群行为与市场波动研究.管理科学学报,2010,13(9):119-128.

CHEN Ying,YUAN Jianhui,LI Xindan,et al.Research on collaborative herding behavior and market volatility:based on computational experiments.JournalofManagementSciencesinChina,2010,13(9):119-128.(in Chinese)

[31] 胡昌生,池阳春．投资者情绪、资产估值与股票市场波动.金融研究,2013(10):181-193.

HU Changsheng,CHI Yangchun.Investor sentiment,asset valuation,and the volatility of stock market.JournalofFinancialResearch,2013(10):181-193.(in Chinese)

[32] 文凤华,肖金利,黄创霞,等.投资者情绪特征对股票价格行为的影响研究.管理科学学报,2014,17(3):60-69.

WEN Fenghua,XIAO Jinli, HUANG Chuangxia, et al. The effects of characteristics of investor sentiment on stock price behaviors.JournalofManagementSciencesinChina,2014,17(3):60-69.(in Chinese)

[33] YANG C,LI J.Investor sentiment,information and asset pricing model.EconomicModelling,2013,35:436-442.

[34] YANG C,LI J.Two-period trading sentiment asset pricing model with information.EconomicModelling,2014,36:1-7.

[35] YANG C,CAI C.Higher order expectations in sentiment asset pricing model.EconomicModelling,2014, 39:95-100.

[36] YANG C,ZHOU L.Investor trading behavior,investor sentiment and asset prices.TheNorthAmericanJournalofEconomicsandFinance,2015,34:42-62.

[37] YANG C,ZHOU L.Sentiment approach to underestimation and overestimation pricing model.EconomicModelling,2015,51:280-288.

[38] 刘祥东,刘澄,刘善存,等.羊群行为加剧股票价格波动吗?.系统工程理论与实践,2014,34(6):1361-1368.

LIU Xiangdong,LIU Cheng,LIU Shancun,et al.Does herd behavior increase stock price volatility?.SystemsEngineering-Theory&Practice,2014,34(6):1361-1368.(in Chinese)

[39] REKIK Y M, HACHICHA W,BOUJELBENE Y.Agent-based modeling and investors′ behavior explanation of asset price dynamics on artificial financial markets.ProcediaEconomicsandFinance,2014,13:30-46.

[40] KENDALL M G,HILL A B.The analysis of economic time-series-part I:prices.JournaloftheRoyalStatisticalSociety.SeriesA(General),1953,116(1):11-34.

[41] DAY R H,HUANG W.Bulls,bears and market sheep.JournalofEconomicBehavior&Organization,1990,14(3):299-329.

StudyonRandomTradingBehavior,HerdBehaviorandAssetPriceVolatility

LIU Gang，HU Wenxiu，ZHANG Weiguo，JIA Lina

Faculty of Economics and Management, Xi′an University of Technology, Xi′an 710054, China

The interplay among random trading behavior, herd behavior and mean-reversion behavior from the traders of a market will cause the change of asset price volatility. However, existing researches mainly focus on the latter two behaviors′ influences on asset price volatility, and few studies are related to random trading behavior.

On the basis of the Behavioral Finance Theory, and through introducing random traders, this paper expands existing nonlinear dynamical model of asset price, which explores the interaction of the random trading behavior and herd behavior as well as mean-reversion behavior and its impact on asset price volatility. Based on the basic hypothesis of the research, it analyzes the path of asset price formation and constructs the corresponding model to make a further analysis on the characteristics of equilibrium point and stability of the financial system. Using the MATLAB software, it tests the asset price volatility by numerical simulation.

It indicates: firstly, because of the existence of random trading behavior in the market, the asset price cannot converge to the fundamental value of asset, but simply an equilibrium price which deviates from fundamental value of the asset. Secondly, when the financial system keeps partial stability, the degree of mean-reversion trading is proportionate to the degree of random trading; the stability region of herd behavior is proportionate to the degree of random trading, inversely proportionate to the degree of mean-reversion, and the asset price will converge to the equilibrium price of assets by spiral damped oscillation movements. Thirdly, there are two situations when the partial financial system is not partially stable: one is stability situation in which the asset price stays slightly floating and periodically vibrated around the asset equilibrium price. the other one is instability situation due to asset price volatility at higher degree. Furthermore, with the increasing degree of random trading in the market, asset equilibrium price which deviates from the fundamental value would be at higher degree.

It reveals the relationship between the three trader behaviors and asset price volatility and improves the system of Behavioral Finance Theory. Meanwhile, it provides some suggestions for the government to stabilize financial market as follows: firstly, the government should cultivate the value investing of the traders and reduce the occurrence of speculation; secondly, the government should also avoid the herd behavior caused by asymmetric information.

asset price volatility；random trading behavior；herd behavior；mean-reversion trading behavior；financial system；local stability

Date:June 11th, 2015

DateMarch 11th, 2016

FundedProject:Supported by the National Natural Science Foundation of China(71373204), the Shaanxi Provincial Education Department of Philosophy and Social Science Research Base of Scientific Research Projects(13JZ036) and the Special Foundation for Construction of Key Discipline in Shaanxi University (107-5X1302)

Biography:LIU Gang is a Ph.D candidate in the Faculty of Economics and Management at Xi′an University of Technology. His research interests cover behavioral finance and asset pricing. E-mail：362390252@qq.com

HU Wenxiu, doctor in management, is a professor in Faculty of Economics and Management at Xi′an University of Technology. His research interests include behavioral finance, financial engineering and risk management. His monograph titledAnalyzingassetbubbleandbubbleeconomywas published by Beijing: Higher Education Press, 2012. E-mail：huwenxiu1964@163.com

ZHANG Weiguo, doctor in management, is a lecturer in Faculty of Economics and Management at Xi′an University of Technology. His research interests include corporate merger and acquisition. He was granted the Postdoctoral Science Foundation Project of China(2015M582691) titled “Social connection between senior executives, enterprise merger transactions and merger performance”. E-mail：wgzhang2006@163.com

JIA Lina is a Ph.D candidate in the Faculty of Economics and Management at Xi′an University of Technology. Her research interests cover financial engineering. Her representative paper titled“Study on the influence of the crowding trade of securities investment funds on stock bubble” was published in theOperationsResearchandManagementScience(Issue 5, 2015). E-mail：379729761@qq.com

F830.91

A

10.3969/j.issn.1672-0334.2016.02.010

1672-0334(2016)02-0122-12

2015-06-11修返日期2016-03-11

国家自然科学基金(71373204)；陕西省教育厅哲学社会科学重点研究基地科学研究计划资助项目(13JZ036)；陕西省普通高校重点学科专项资金建设资助项目(107-5X1302)

刘刚，西安理工大学经济与管理学院博士研究生，研究方向为行为金融和资产定价等，E-mail：362390252@qq.com

扈文秀，管理学博士，西安理工大学经济与管理学院教授，研究方向为行为金融、金融工程和风险管理等，代表性学术成果为2012年由高等教育出版社出版的论著《透视泡沫：资产泡沫与泡沫经济》，E-mail：huwenxiu1964@163.com

章伟果，管理学博士，西安理工大学经济与管理学院讲师，研究方向企业并购与重组等，代表性学术成果为中国博士后科学基金项目(2015M582691)“高管间社会联结、企业并购交易和并购绩效研究”，E-mail：wgzhang2006@163.com

贾丽娜，西安理工大学经济与管理学院博士研究生，研究方向为金融工程等，代表性学术成果为“基金‘拥挤交易’对A股股价泡沫的影响研究”，发表在2015年第5期《运筹与管理》，E-mail：379729761@qq.com

□