舌簧阀升程限制器线型设计方法*

丁兴宇 米小珍 王 枫

(大连交通大学交通运输工程学院)

舌簧阀升程限制器线型设计方法*

丁兴宇*米小珍 王 枫

(大连交通大学交通运输工程学院)

为了对升程限制器的线型设计方法进行系统分析，对比了悬臂梁法、振动力学法和有限元法3种理论线型设计方法。为了保证理论线型的精度，同时又便于实际加工，对比分析了直线型和单曲率直线型升程限制器理论线型拟合方法。实验结果表明：单曲率直线拟合的有限元法升程限制器理论线型既能保证理论线型的精度，又能有效减小应力集中，提高阀片使用寿命。

舌簧阀 升程限制器 理论线型设计 线型拟合

气阀工作时，如果阀片撞击升程限制器的运动规律与升程限制器的线型贴合较好，则二者之间的接触附加应力较小，可以减少阀片磨损，提高阀片的使用寿命。另外，升程限制器还影响工质的有效通流面积，增加升程可以增大气阀的通流截面，降低功率损失，但是升程过大将使阀片与升程限制器的撞击速度增大，降低阀片的使用寿命。因此，升程限制器的设计不仅要确定合理的升程，满足阀片开启流通面积的需求，而且要确定合理的线型，这样才能既保证气阀的效率，又满足使用寿命和可靠性的需求[1]。

国内早有学者对升程限制器进行了研究，陈天及提出了一种增大舌簧阀有效通流面积、减小阀片变形的单曲率直线型升程限制器和条状簧片阀升程限制器曲率的工程计算方法[2]。郑学鹏等利用数值计算方法比较了圆弧型和斜面型舌簧阀升程限制器，发现斜面型升程限制器的阀片根部应力远大于圆弧型升程限制器，而斜面型升程限制器更可靠、不易变形[3]。张春安通过数值计算方法得出在曲柄角速度、阀片等效质量等因素不变的情况下，阀片的撞击速度主要取决于阀片的升程，并推荐了舌簧阀升程和撞击速度的取值范围[4]。覃凤敏通过有限元分析，对传统的往复式压缩机网状阀的阀座和升程限制器计算公式进行了修正，修正后的公式能较好地考虑升程限制器径向筋相对宽度的影响[5]。袁秀玲等对环状阀的吸排气阀片厚度、气阀升程及阀弹簧刚度等结构参数进行了优化设计，采用改进的Swift法，缩短了计算时间，改善了解的稳定性[6]。Kwon Y K等在考虑材料韧性和可靠性的基础上，对Sandvik 20C材料的升程限制器进行了金相分析，对往复式压缩机和阀片进行了设计分析，发现升程限制器的长度越短，在稳定性方面的表现越好，升程限制器的长度越长，在压缩机运行上的表现越好[7]。Kim J Y等通过ADINA仿真，运用接触分析方法计算了某排气阀片升程限制器的最大接触应力，为升程限制器的结构稳定性分析提供了新的分析方法[8]。冯爱玉和刘浩提出增大气阀通流面积可以使阀隙马赫数下降，从而提高微型压缩机舌簧阀的寿命。但是增大升程又增加了阀片撞击速度，反而会增大阀片的磨损[9]。

上述研究虽涉及到升程限制器，但并未针对其线型设计方法进行系统分析，也缺乏考虑工程实际应用和加工对升程限制器线型设计的需求。为此，笔者针对实际加工的需求，采用单曲率直线对升程限制器理论线型进行拟合，在保证理论线型精度的同时，减小应力集中，提高阀片使用寿命。

1 升程限制器理论线型设计方法

舌簧阀构成的气阀组件结构示意图如图1所示，其中，H为最大升程，los为阀片特征升程，La为阀孔中心到定位螺栓的距离，LA为阀片顶端到定位螺栓的距离。当气缸内压强大于外界压强与阀片刚度时阀片开启，此时阀片受到的外力可以近似为集中载荷F1。为了减少阀片与限制器撞击时的附加载荷，限制器的线型应尽量与阀片运动规律相吻合，因此限制器线型设计首先要进行阀片受力分析。常用的阀片受力分析方法有悬臂梁法[10]、振动力学法[2]和有限元法[3]。

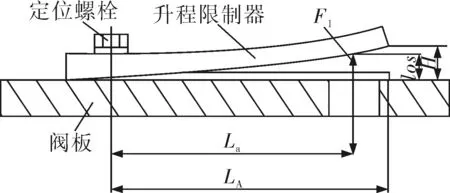
图1 气阀组件结构示意图

1.1悬臂梁法

由于阀片一端用螺栓固定在阀板上，另一端可在竖直方向上自由运动，所以其模型可简化为如图2所示的悬臂梁模型。

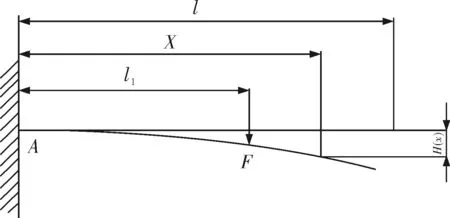
图2 阀片的悬臂梁模型

由材料力学基本知识可得悬臂梁挠度H(x)为[10]：

(1)

式中E——弹性模量，Pa；

F——力，N；

I——惯性矩，m4；

l——悬臂梁总长，m；

l1——固定端到施力点的距离，m；

x——计算点到固定端的距离，m。

当式(1)中的x=La时，挠度值H(x)即为气阀的特征升程los，则式(1)可变为：

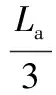
(2)

其中，最大升程H与阀片受力、弹性模量和惯性矩有关，实际设计中通常采用类比方法确定一个经验值。

为便于比较研究，现针对某一特定排气阀片进行分析。图3所示为某压缩机排气阀片模型，其尺寸参数为：La=34.50mm，LA=43.75mm，H=3.70mm。

图3 某压缩机排气阀片模型

将已知数据代入式(2)，即可得到排气阀的特征升程los=264mm。

将已知量代入式(1)可以获得阀片处于最大开启位置时的阀片变形曲线，即悬臂梁法计算得到的升程限制器理论线型：

(3)

1.2振动力学法

悬臂梁法将阀片简化为一端固定的梁模型，未考虑阀片的宽度，这将影响阀片刚度的计算，使计算结果误差较大。由于阀片长度大于宽度和厚度，所以振动力学法将图1所示的阀片模型简化为条状矩形一阶横振动主振型进行分析。根据振动力学理论，可建立如下关系[2]：

H(x)=c×[-1.3622(cos(bx)-ch(bx))+

sin(bx)-sh(bx)]

(4)

其中，b=1.8751/LA，c=H/2.725。代入阀片已知参数，可得到特征升程los=2.626mm。

由式(4)可得到阀片在最大位移时的变形曲线，即升程限制器的理论线型：

h(x)=1.3578×[-1.3622(cos(42.86x)-

ch(42.86x))+sin(42.86x)-sh(42.86x)]

(5)

1.3有限元法

相对于悬臂梁法和振动力学法，有限元法充分考虑了阀片的几何形状对变形的影响，所以有限元法可近似地模拟实际变形。

有限元基本方程为：

Fe=Kδe=BTDB

(6)

式中B——应变矩阵；

D——弹性矩阵；

Fe——载荷矩阵；

K——总体刚度矩阵；

δe——位移矩阵。

其中，总体刚度矩阵由每个单元刚度矩阵求得。已知材料属性可以求得应变矩阵、弹性矩阵和单元刚度矩阵。如果载荷矩阵已知，可以得出各单元节点的位移。

图4为阀片有限元模型及其在Ansys中的载荷。其中，A为定位螺孔，为固定支点；B为加载区，等于阀板排气孔的面积。阀片所受的均布载荷为阀片最大升程H=3.70mm时所施加的值，这样可以求得特征升程los=2.59mm。

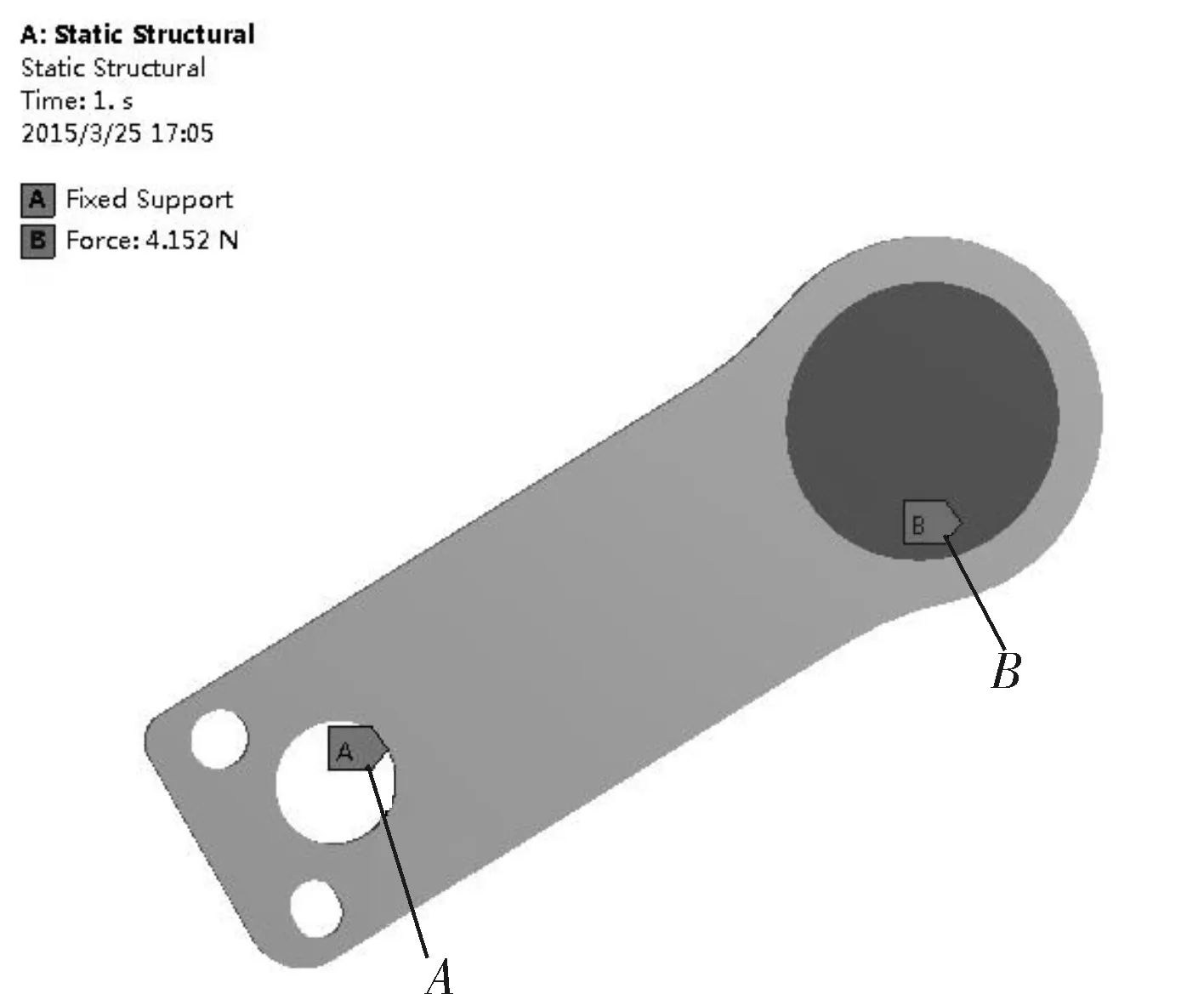
图4 阀片有限元模型

图5所示为有限元法获得的阀片变形云图，由此可以得到阀片升程限制器的线型。

图5 阀片变形云图

1.43种方法的比较

由材料力学可知，悬臂梁法忽略了阀片宽度和厚度的影响，将阀片简化为一端固定的梁模型进行计算；振动力学法考虑了阀片的宽度，将阀片简化为矩形进行计算，因此该方法考虑了模态的部分影响；有限元法综合考虑了阀片的形状和尺寸因素，因此仿真分析结果更加接近阀片的实际受力和变形。3种不同方法获得的阀片变形曲线，即升程限制器理论线型如图6所示。

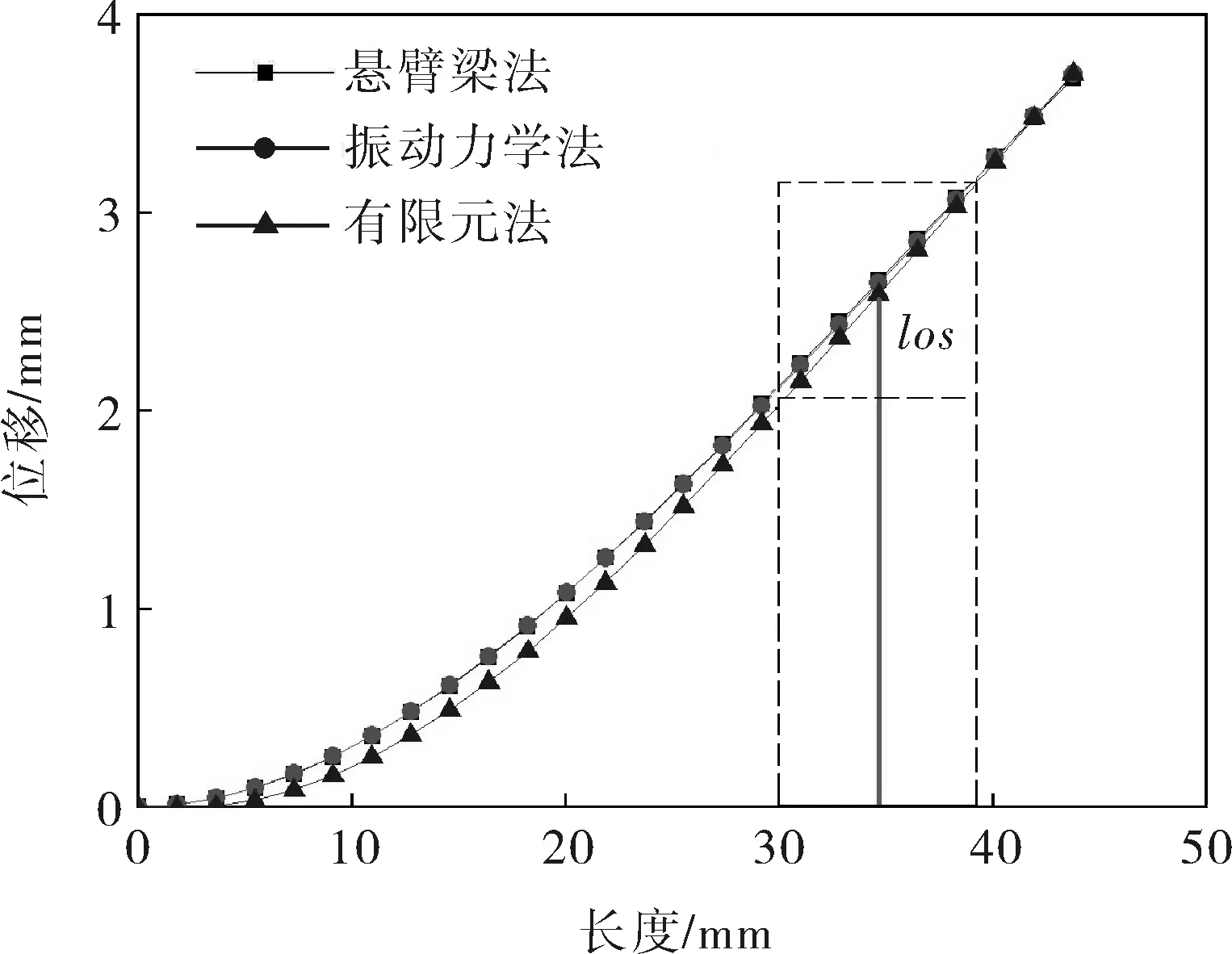
图6 3种方法的升程限制器理论线型

由于有限元法更能较为精确地反映阀片运动的真实情况，所以笔者采用有限元法作为基准来对比研究其他两种数值方法所获得的限制器线型。以误差值小于0.01%为标准，对3种线型进行分析，结果见表1。

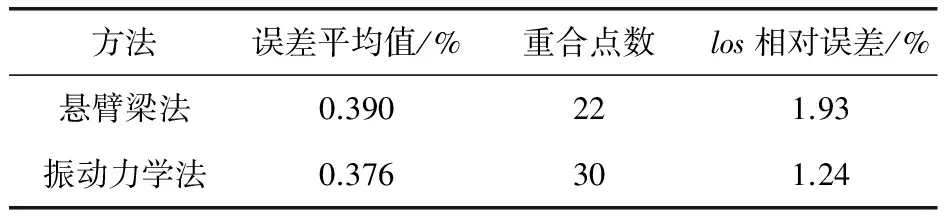
表1 3种方法的对比分析结果

由表1可知，悬臂梁法和振动力学法计算的阀片特征升程与有限元法的相对偏差小于2.00%，说明采用3种方法获得的气阀特征升程均可以满足设计要求，且振动力学法获得的线型与有限元法更接近(两者之间有30点重合)。由于悬臂梁法计算相对简单，在产品初期设计阶段可以采用此方法，而振动力学法和有限元法更适用于产品的详细设计阶段。

2 线型拟合方法

虽然悬臂梁法和振动力学法可以计算出阀片的理论线型方程，但直接采用该方程加工升程限制器较为困难，所以在实际加工中一般用较为简单的直线(直线型升程限制器)或圆弧(单曲率直线型升程限制器)去拟合阀片变形曲线。因此，笔者采用线性方程和圆弧方程对有限元法计算的阀片线型方程进行拟合，以得出适合工程应用的线型拟合方法。

图7所示为两种线型拟合方法得到的位移残差拟合曲线。

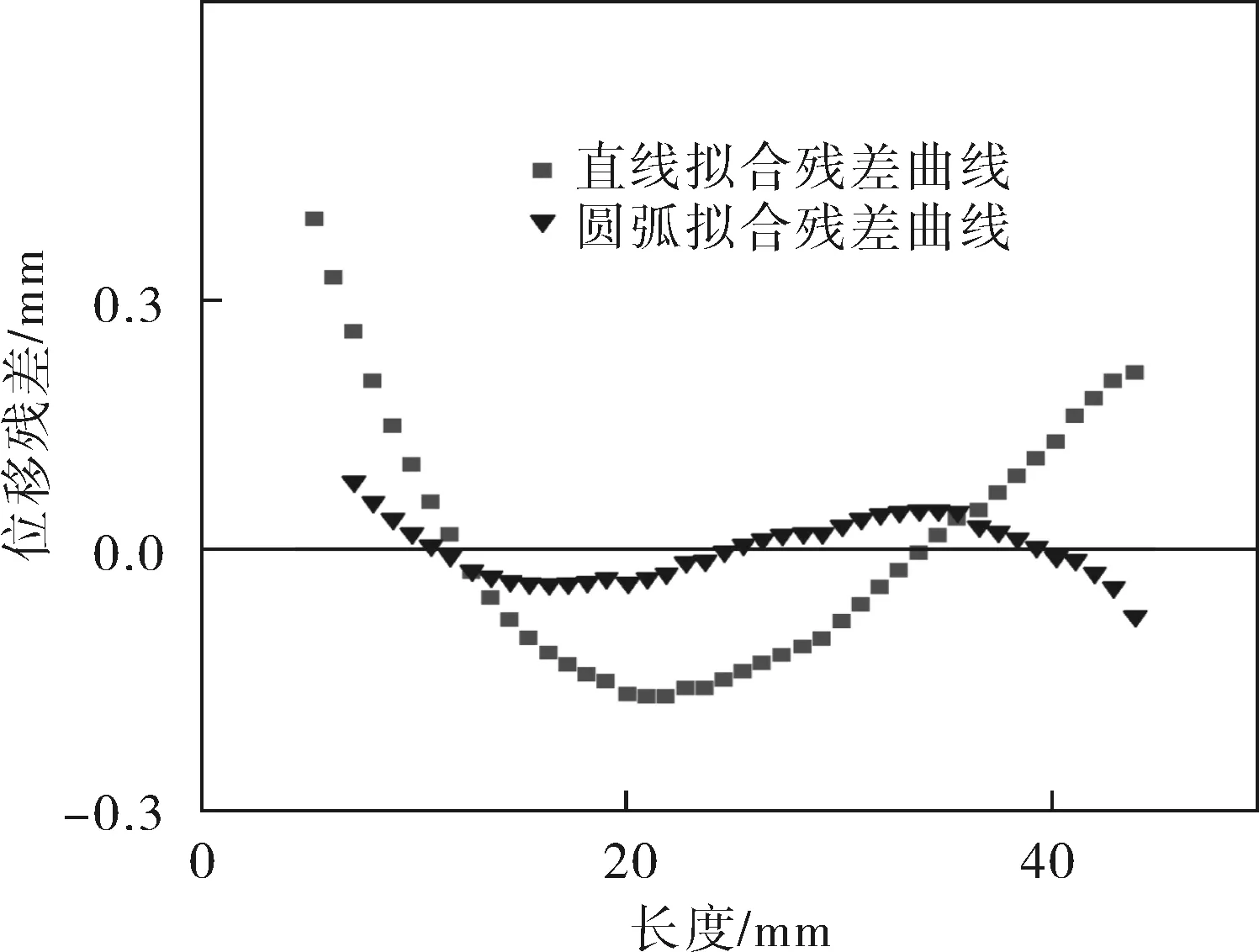
图7 两种线型拟合方法得到的位移残差拟合曲线

根据图7中数据可以计算得出，用直线拟合时位移残差的平方和为8.93×10-7，用圆弧拟合时残差的平方和为1.30×10-7，前者为后者的6.87倍。虽然直线拟合方法简单，但是残差大，与理论线型偏离较大，而且阀片与升程器根部贴合时容易产生应力集中，增加阀片磨损。而采用单曲率型拟合法获得的升程限制器可以较好地贴合阀片变形曲线，有利于减小阀片磨损，提高使用寿命，而且相对于理论线型更便于实际加工。

3 实验验证

为了进一步分析升程限制器线型对压缩机性能和阀片使用寿命的影响，以某型号压缩机为例，分别测试直线型和单曲率直线型升程限制器对阀片的磨损情况。测试工况为冷凝温度40.5℃，蒸发温度-30.0℃，吸气温度18.3℃。运转20h后，阀片的使用情况如图8所示。

图8 阀片根部磨损情况对比

从图8a可以看出，直线型升程限制器上的阀片在根部有较明显的磨损。相对于直线型升程限制器，由于单曲率直线型升程限制器可以很好地贴合阀片变形曲线，从而减小了阀片撞击升程限制器时的附加应力，提高了阀片的使用寿命，由此也验证了笔者提出的阀片线型设计方法和拟合方法的合理性。

4 结论

4.1悬臂梁法、振动力学法和有限元法获得的限制器特征升程差异较小，均能满足气阀设计的基本要求。

4.2悬臂梁法计算相对简单，在产品初期设计阶段可以采用此方法进行升程限制器的线型设计。

4.3由于模型简化时考虑的因素不同，振动力学法与有限元法获得的线型更接近，这两种方法获得的线型与阀片运动规律更加吻合，更适用于产品详细设计阶段。

4.4面向工程设计时，在理论线型的基础上，采用单曲率直线进行拟合，既能保证理论线型的精度，又能有效地减小应力集中，提高阀片使用寿命，而且可以应用于工程设计中。

[1] 缪道平,吴业正.制冷压缩机[M].北京:机械工业出版社,2004.

[2] 陈天及.压缩机舌簧阀升程限制器的设计[J].流体机械,1994,22(1):38～40.

[3] 郑学鹏,王存智,郭秀萍.舌簧阀升程限制器型线研究[J].压缩机技术,1999,(6):7～10.

[4] 张春安.舌簧阀片升程对使用寿命的影响[J].流体机械,1998,26(6):45～47.

[5] 覃凤敏.往复式压缩机网状阀阀座与升程限制器强度研究及应用[D].南宁:广西大学,2008.

[6] 袁秀玲,张华俊,许晶华,等.活塞式制冷压缩机气阀参数的优化设计[J].流体工程,1993,21(5):49～55.

[7] Kwon Y K,Lee G H,Lee T J.The Design of Compressor Valve to Consider the Flexibility and Reliability[C]. International Compressor Engineering Conference. West Lafayette:Purdue University,2004:1～5.

[8] Kim J Y,Park S G,Oh I K.Fluid Structure Interaction Analysis of a Reciprocation Compressor[C].The Sixteenth International Congress on Sound and Vibration.Krakow:International Institute of Acoustics and Vibration,2009:4～7.

[9] 冯爱玉,刘浩.提高微型压缩机舌簧阀性能与寿命[J].机电设备,1987,(5):9～10.

[10] 林梅，郁永章.容积式压缩机技术手册[M].北京:机械工业出版社,2000:328～368.

DesignMethodforReedValveLiftLimiterLinetype

DING Xing-yu, MI Xiao-zhen, WANG Feng
(SchoolofTrafficandTransportation,DalianJiaotongUniversity,Dalian116028,China)

For the purpose of systematically analyzing the linetype design method for the reed valve’s lift limiter, the beam method, vibration mechanics method and finite element method were analyzed and compared, including the theoretical linetype fitting method for the linear-typed lift limiter and the single curvature straight line-typed lift limiter to ensure theoretical linetype’s precision and to benefit its machining process. The experimental results show that the theoretical linetype of FEM-based lift limiters which featuring single-curvature straight-line fitting can ensure linetype’s precision and reduce stress concentration as well as improve valve disc’s servicing life.

reed valve, lift limiter, theoretical linetype design, linetype fitting

* 国家自然科学基金资助项目(51205035)，辽宁省教育厅资助项目(L2013173)。

** 丁兴宇，男，1990年7月生，硕士研究生。辽宁省大连市，116028。

TQ055.8+1

A

0254-6094(2016)02-0178-05

2015-04-24，

2015-05-20)