弹性约束下颗粒碰撞阻尼器的理论与实验研究

杜妍辰 秦 婧

上海理工大学，上海，200093



弹性约束下颗粒碰撞阻尼器的理论与实验研究

杜妍辰 秦 婧

上海理工大学，上海，200093

为进一步研究弹性约束颗粒碰撞阻尼器的减振性能，提出了该阻尼系统的动力学模型，并模拟了该阻尼器对悬臂梁的减振效果。同时，对5种不同刚度的弹性约束颗粒碰撞阻尼器的减振效果进行了实验研究。结果表明：理论计算与实验的结果基本吻合，证明所建立的弹性约束下的颗粒碰撞阻尼系统的计算模型是可靠的；在弹性约束下的颗粒碰撞阻尼系统中，其刚度比对减振效果的影响是非线性的，且弹簧刚度对该碰撞系统的共振点存在影响。

弹性约束；颗粒碰撞阻尼；动力学模型；刚度比

0 引言

阻尼技术能将动能转化为热能或其他能量进行耗散，达到减振、降噪的目的，已被广泛应用于航空、机械、汽车和土木工程等领域。碰撞阻尼器是传统减振器中最典型的一种，利用冲击器与腔体之间连续的非弹性碰撞进行动量交换，不断地吸收、扩散和耗散能量，来抑制主系统的响应[1-4]，但部分能量会回到主系统中，致使能量耗散效果

不理想。20世纪末，Panossian[5]最先提出了颗粒阻尼的概念，以铝制悬臂梁为研究对象，进行了微颗粒阻尼实验。随后柔性颗粒阻尼[6]、颗粒阻尼[7-8]、颗粒碰撞阻尼[9-11]概念相继提出。颗粒碰撞阻尼的原理是在碰撞阻尼的基础上加入颗粒减振剂，通过腔体内部钢球与颗粒减振剂的相互碰撞使颗粒产生塑性变形来吸收和消耗系统能量。试验结果证明[12-17]，与传统的碰撞阻尼器相比，在自由衰减和强迫激励振动中，颗粒碰撞阻尼器的减振效果、降低冲击噪声效果均更为显著、有效。但它也存在一系列的问题，比如腔体内减振剂颗粒松散、运动不确定等造成阻尼系统复杂，难以精确求解和实时仿真。另一方面，有研究发现弹簧的储能特性能快速地减小加速度峰值，若将弹性储能特性和塑性耗能特性有机结合起来，必定能达到更好的减振效果。

1 弹性约束下颗粒碰撞阻尼器的结构及减振机理

弹性约束下的颗粒碰撞阻尼器是一种具有两级减振结构的新型碰撞阻尼器，它在带颗粒减振剂碰撞阻尼器的基础上增加了弹性约束，结合了弹性约束和塑性变形。如图1所示，该阻尼器由内外两层结构组成，内层腔体中加入微细颗粒减振剂及钢球，利用两者的相互撞击，使颗粒产生塑性变形，同时通过内部摩擦，永久地耗散能量。外层附带弹簧约束，利用弹簧的动力放大作用，加大腔体内颗粒间的相互碰撞和塑性变形；同时，弹簧积累能量并将能量转移到腔体，实现阻尼器和主系统之间的动量交互最大化，从而达到两级减振的目的[18]。与带颗粒减振剂的碰撞阻尼器相比，这种两层结构的碰撞阻尼器具有更广阔的应用前景。

图1 弹性约束下的颗粒碰撞阻尼器三维图

2 弹性约束下的颗粒碰撞阻尼系统计算模型

2.1 动力学模型

为进一步分析弹性约束下的颗粒碰撞阻尼振动系统的动力学特性，建立了一个动力学模型。如图2所示，该系统由主质量M、等效刚度K和系统阻尼C组成，主振体在持续的激振力F0sinωt作用下产生振动，其中，F0为激振力幅值。

2.2 运动微分方程

图2所示的模型中，将钢球和主振体视为2个完全独立的物体，它们的运动规律互不影响，仅在相互碰撞时存在关系。假定整个实验过程中的能量耗散以碰撞耗能为主，阻尼器各组成部件之间的摩擦忽略不计；碰撞为非弹性碰撞，只考虑水平方向的振动。则在不发生碰撞时，主振体的运动微分方程为[19]

(1)

由式(1)得到主系统稳态响应：

x=Bsin(ωt-ψ)

(2)

(3)

(4)

式中，ω为激励力的频率；λ为频率比，λ=ω/ωn；ωn为固有频率；ξ为系统阻尼比，ξ=c/(2meωn)。

2.3 求解方法与过程

2.3.1 系统等效质量与等效刚度的计算

分别称量实验中悬臂梁的质量ma与末端集中质量mb，则等效质量[20]

M=0.23ma+mb

(5)

测量悬臂梁尺寸，根据下式计算悬臂梁刚度：

k1=3EI/L3

(6)

式中，E为弹性模量；I为悬臂梁的截面惯性矩；L为悬臂梁长度。

2.3.2 系统等效阻尼的计算

该弹性约束下颗粒碰撞阻尼系统约化一阶阻尼系数

(7)

ψb=4πξ1

(8)

ξ1=δ/(2π)

(9)

(10)

ψp=ΔT/T

(11)

式中，ψb为悬臂梁的固有阻尼；A1为悬臂梁自由衰减振动图中的第一个峰值；An为悬臂梁自由衰减振动图中的第n个峰值，n=4，5，…；ψp为阻尼比容，定义为单个循环中的动能耗散与整个循环中的最大动能的比值；ΔT为单个循环中的动能耗散；T为整个循环中的最大动能。

(12)

(13)

式中，mp为阻尼器腔体内微颗粒的质量；e为整个碰撞过程中的恢复系数[21]。

循环中最大动能T在主系统速度达到最大时取最大值，即有

(14)

3 数值计算与实验结果对比分析

3.1 实验装置

本实验将悬臂梁等效成弹簧-质点系统，通过模拟计算结果与实验结果的对比分析，验证提出的一维碰撞模型。实验过程中，将悬臂梁一端固定，采用高频电磁激振器对其固定端根部进行正弦激振。弹性约束下的颗粒碰撞阻尼器置于悬臂梁的自由末端，加速度传感器固定在阻尼器的对面，如图3所示，通过信号采集器采集加速度信号，经二次积分或拉普拉斯变换得到时间-位移图或频率-位移图。

图3 实验装置示意图

实验用悬臂梁的尺寸为315 mm×45 mm×2.1 mm，材料为A3钢，密度7.8×103kg/m3。阻尼腔体为内径12 mm、高20 mm的圆柱形腔体(内置8个直径5 mm钢球)，采用粒度56 μm的锌粉颗粒填充，填充率为20%。

3.2 实验方案

实验包括两部分：一是自由衰减实验，分别采集在无阻尼和弹性约束颗粒碰撞阻尼作用下的悬臂梁加速度信号，并对加速度信号进行数据处理与分析。二是受迫振动实验，在简谐激励力作用下，分别对不同阻尼(表1)及5种不同刚度比的弹性约束颗粒碰撞阻尼条件下悬臂梁的最大振幅进行采集和比较分析，其中，刚度比定义为弹簧刚度与悬臂梁主梁刚度的比值。实验前期通过扫频方式分别对两组受迫振动实验的系统固有频率进行预测定，再依据测得的固有频率进行实验频率的设定，获得相应的最大振幅幅值。

表1 实验装置的各部件参数

3.3 实验结果与讨论

图4所示为悬臂梁在无阻尼和弹性约束颗粒碰撞阻尼作用下(计算结果和实验结果)的自由衰减曲线图。从图4可看出，弹性约束颗粒碰撞阻尼下的计算结果曲线与实验结果曲线在相同时间点或相近时间点出现峰值，且基本趋势走向一致。但衰减前期的计算值相对实验值偏大，这是由理论模型的简化和具体实验过程中不可避免的摩擦和阻力导致的。衰减后期的计算值相对实验值偏小，其主要原因是阻尼器存在惯性力，致使实际悬臂梁的衰减速度变缓。以上讨论证明了本文建立的运动学模型可用于弹性约束下的颗粒碰撞阻尼器的模拟。

比较图4中无附加阻尼和弹性约束颗粒碰撞阻尼作用下悬臂梁的自由衰减曲线，可发现两者差异显著。在相同的初始加速度条件下，附加弹性约束下颗粒碰撞阻尼时悬臂梁的衰减呈现显著下降趋势，至1.8s末，弹性约束下颗粒碰撞阻尼的衰减率为94.8%，远远高于无附加阻尼时悬臂梁的衰减率67.9%。由此可知，弹性约束下的颗粒碰撞阻尼能有效减小悬臂梁的响应幅值，且减振效果良好。

(a) 悬臂梁自由衰减

(b) 弹性约束下颗粒碰撞阻尼自由自由衰减计算值

图5 受迫振动时理论计算结果与实验结果比较

图5所示为无阻尼、碰撞阻尼和弹性约束颗粒碰撞阻尼条件下，悬臂梁受迫振动的理论计算结果与实验结果。从图5可知，3种阻尼条件下的计算结果曲线与实验结果曲线变化趋势基本一致。实验结果显示，碰撞阻尼最大振幅较无阻尼情况下减小了43.6%，弹性约束颗粒碰撞阻尼最大振幅较无阻尼情况下减小了74.8%，表明弹性约束颗粒碰撞阻尼器通过弹性约束与颗粒塑性变形来转移、储存和耗散能量的减振机理，能够促进悬臂梁更快地衰减，从而取得更优异的减振效果。弹性约束颗粒碰撞减振效果更优的原因是：①加入弹簧后，阻尼器中的冲击器与腔体两端的撞击次数增加，动量交换次数增加,同时，由于弹簧的引入，阻尼腔体可以将部分能量传递给弹簧。②在弹簧储存和释放能量的过程中，弹簧与支架、弹簧与悬臂梁间会产生摩擦，通过热能的形式耗散系统的小部分能量。从弹性约束颗粒碰撞阻尼器作用下悬臂梁受迫振动的计算结果和实验结果可以看出，最大振幅在频率12.2 Hz、12.1 Hz处出现峰值，振幅对应为5.25 mm、5.60 mm，误差小于7%。由此可证明本文建立的运动模型及运动微分方程是可靠的，可以用来对弹性约束下颗粒碰撞阻尼进行理论模拟。

图6、图7分别为不同刚度比条件下悬臂梁末端振幅模拟结果和实验结果。从图7可以看出，随着刚度比的增大，共振点往高频率方向发生迁移，与模拟结果(图6)基本吻合。模拟结果的最大振幅比实验结果略微偏大，这是因为模拟时将系统模型进行了简化，忽略了阻尼腔体刚度及零件间相互摩擦。综合图6、图7可以看出，对于部分结构确定的弹性约束颗粒碰撞阻尼器，其刚度比对减振效果影响是非线性的，存在一个最佳的刚度比。这是因为弹簧刚度太小，不能起到能量储存及能量转换的作用，并且较小的弹簧刚度无法缓冲和支撑端部的阻尼器腔体，容易引起混沌现象；弹簧刚度太大，中间腔体的活动减缓，减少了冲击器与容器壁的撞击，耗能减少。但随着激振时间的延长，腔体内粉末颗粒是否因碰撞时间过长造成破碎，无法达到塑性形变而降低减振效果，有待进一步研究。

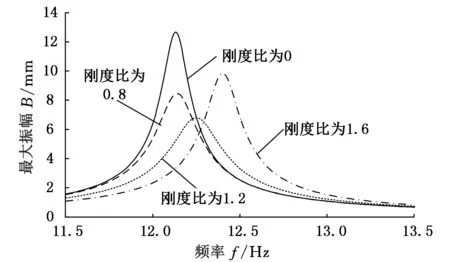
图6 不同刚度比条件下悬臂梁末端振幅模拟结果

图7 不同刚度比条件下悬臂梁末端振幅实验结果

4 结论

(1)理论计算与实验结果基本吻合，证明了本文建立的弹性约束颗粒碰撞阻尼的计算模型是可靠的。

(2)对不同刚度比条件下弹性约束颗粒碰撞阻尼减振进行的数值模拟和实验研究结果显示，在弹性约束颗粒碰撞阻尼系统中，其刚度比对减振效果的影响是非线性的，且弹簧刚度对该碰撞系统的共振频率点存在影响。

[1] Li K, Darby A P. Experiments on the Effect of an Impact Damper on a Multiple Degree of Freedom System[J]. Journal of Vibration and Control, 2006, 12 (5): 445-464.

[2] Nigm M M, Shabana A A. Effect of an Impact Damper on a Multi-degree of Freedom System[J]. Journal of Sound and Vibration, 1983, 89(4): 541-557.

[3] Gharib M, Karkoub M. Shock-based Experimental Investigation of the Linear Particle Chain Impact Damper[J]. Journal of Vibration and Acoustics, 2015, 137(6): 061012-1-10.

[4] 王栋. 冲击减振器对振动能量耗散性能分析[J]. 机械工程学报, 2014, 50(17): 87-92. Wang Dong. Analysis of Vibration Energy Dissipation with Vibro-impact Absorber[J]. Journal of Mechanical Engineering, 2014, 50(17): 87-92.

[5] Panossian H V. Non-obstructive Particle Damping Performance under Compaction Forces[J]. Machinery Dynamics and Element Vibrations, 1991, 36: 17-20.

[6] Popplewell N, Semercigil S E. Performance of the Bean Bag Impact Damper for a Sinusoidal External Force[J].Journal of Sound and Vibration, 1989, 133(2): 193-223.

[7] 鲁正, 吕西林, 闫维明. 颗粒阻尼技术研究综述[J]. 振动与冲击, 2013, 32(7): 1-7. Lu Zheng, Lü Xilin, Yan Weiming. A Survey of Particle Damping Technology[J]. Journal of Vibration and Shock, 2013, 32(7):1-7.

[8] 马崇武, 慕青松. 颗粒阻尼器对悬臂梁自由振动的被动减振作用[J]. 兰州理工大学学报, 2014, 40(3): 165-168. Ma Chongwu, Mu Qingsong. Passive Damping Effect of Particle Damper on Free Vibration of a Cantilever Beam[J]. Journal of Lanzhou University of Technology, 2014, 40(3): 165-168.

[9] Abdel-Gawad M. Passive Vibration Damping with Noncohesive Granular Materials[C]//Proceedings of Damping. San Diego, California, 1991: GDB1-14.

[10] 杜妍辰, 王树林, 朱岩, 等. 带颗粒减振剂碰撞阻尼的减振特性[J]. 机械工程学报, 2008, 44(7): 186-189. Du Yanchen, Wang Shunlin, Zhu Yan, et al. Vibration Characteristics of a New Fine Particle Impact Damping[J]. Journal of Mechanical Engineering, 2008, 44(7): 186-189.

[11] 杨智春, 李泽江. 颗粒碰撞阻尼动力吸振器的设计及实验研究[J]. 振动与冲击, 2010, 29(6): 69-71. Yang Zhichun, Li Zejiang. Experimental Research and Design of a Particle Impact Damping Dynamic Vibration Absorber[J]. Journal of Vibration and Shock, 2010, 29(6): 69-71.

[12] 姜泽辉, 王运鹰, 吴晶. 窄振动颗粒床中的运动模式[J]. 物理学报, 2006, 55(9): 4748-4753. Jiang Zehui, Wang Yunying, Wu Jing. Motion Modes of Granular Particles in a Vibrating Narrow Tube[J]. Acta Physica Sinica, 2006, 55(9):4748-4753.

[13] 崔体运, 王树林, 刘杰. 颗粒碰撞阻尼器减振性能试验研究[J]. 矿山机械, 2010, 38(12): 51-54. Cui Tiyun, Wang Shulin, Liu Jie. Experimental Study on Damping Performance of Impact Damper with Particles[J]. Mining & Processing Equipment, 2010, 38(12): 51-54.

[14] Duncan M R, Wassgren C R, Krousgrill C M.The Damping Performance of a Single Particle Impact Damper[J]. Journal of Sound and Vibration, 2005, 286(1):123-144.

[15] Marhadi K S, Kinra V K. Particle Impact Damping: Effect of Mass Ratio, Material, and Shape[J]. Journal of Sound and Vibration, 2005, 283: 433-448.

[16] Trigui M, Foltete E, Bouhaddi N. Prediction of the Dynamic Response of a Plate Treated by Particle Impact Damper[J]. Mechanical Engineering Science, 2014, 228(5): 799-814.

[17] 杜妍辰, 张铭命. 带颗粒减振剂的碰撞阻尼的理论与实验[J]. 航空动力学报, 2012, 27(4): 789-794. Du Yanchen, Zhang Mingming. Theoretical and Experimental Research on Impact Damping with Fine Particles as Damping Agent[J]. Journal of Aerospace Power, 2012, 27(4): 789-794.

[18] 杜妍辰, 刘喆, 李海超. 带弹性支承的颗粒-钢球碰撞阻尼的实验研究[J]. 振动与冲击, 2013, 32(24) :56-60. Du Yanchen, Liu Zhe, Li Haichao. Tests for a Particle-ball Impact Damper with Elastic Support[J]. Journal of Vibration and Shock, 2013, 32(24): 56-60.

[19] Blazejczyk-Okolewska B. Analysis of an Impact Damper of Vibrations[J]. Chaos, Solitons and Fractals, 2001, 12(11): 1983-1988.

[20] Trigui M, Foltete E, Abbes M S, et al. Experimental Study of a Multi-particle Impact Damper[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2009, 223 (9): 2029-2038.

[21] 黄揩, 缪国庆, 魏荣爵. 垂直激励下颗粒物质的质心动力学特性[C]//全国物理声学会议论文集. 北京: 中国声学学会，2004: 9-10.

(编辑 张 洋)

Theoretical and Experimental Investigations of Particle Impact Damper with Elastic Restraints

Du Yanchen Qin Jing

University of Shanghai for Science and Technology，Shanghai，200093

In order to study the vibration reduction effects of particle impact damper with elastic restraints on cantilever beam, a dynamics model of the damper was proposed, and its damping performance was simulated by numerical calculations. At the same time, the damping effects of 5 different stiffnesses of the particle impact damper with elastic restraints were studied experimentally. The results show that the calculated results are in good agreement with the experimental ones, indicating that the dynamics model established is reliable. And in the particle impact damper system with elastic restraints, the damping effects of spring stiffness ratio are nonlinear, and the spring stiffness has effects on the resonance point of the collision system.

elastic restraint; particle impact damper; dynamics model; stiffness ratio

2015-12-31

国家自然科学基金资助项目(51475308)

TB535

10.3969/j.issn.1004-132X.2016.21.016

杜妍辰，女，1976年生。上海理工大学医疗器械与食品学院副教授。主要研究方向为振动控制与利用。发表论文20余篇。秦 婧，女，1989年生。上海理工大学医疗器械与食品学院硕士研究生。