偏心摆动油气混输泵的动力特性研究

吉效科 梁 政

1.西南石油大学,成都，610500； 2.长庆油田公司，西安，710018



偏心摆动油气混输泵的动力特性研究

吉效科1,2梁 政1

1.西南石油大学,成都，610500； 2.长庆油田公司，西安，710018

介绍了偏心摆动油气混输泵的工作原理及结构特点，建立了其运动部件的动力学模型，并对已建立的动力学模型进行了数值计算，最后用实验对理论模型进行验证。结果表明：作用在摆轴上的压差作用力所形成的阻力矩是影响混输泵轴功率的主要因素；进出口压差为1.2～3MPa时，计算功率与实验功率的相对偏差为1%～38.2%。

偏心摆动油气混输泵；滑板；摆轴；动力学

0 引言

油气混输技术是油田伴生气回收利用的主要技术。国内应用较广的油气混输泵有双螺杆油气混输泵和单螺杆油气混输泵。它们各有优缺点，其中,双螺杆油气混输泵能够输送含气率高、黏度大的介质，它利用气体的压缩性降低回流损失，提高了容积效率，但是这种泵对固体颗粒敏感，部件寿命短、可靠性低,维护运行成本高。单螺杆油气混输泵主要适用于低排量的油气混输，由于国产橡胶定子材料性能较差，导致高压力(大于3.0 MPa)、高含气量(大于50%)、高含水工况下定子故障较多。

近年来，国内多家公司开展了同步回转油气混输泵的研究[1-3]，取得了一定的成果，但是该泵滑板寿命短等问题始终没有得到很好的解决[4-5]，导致故障率高，无法满足现场生产的需要。笔者设计出一种新型的偏心摆动油气混输泵，它弥补了同步回转油气混输泵的不足，可适应复杂多变的油气混输工况。该泵具有结构简单、部件寿命长、容积效率高、对固体颗粒不敏感等显著特点，可输送高含气率的工作介质，能满足油田低排量、复杂工况的油气混输，较好地解决油田伴生气的回收利用难题。

目前，国内外关于偏心摆动油气混输泵的技术研究处于空白，笔者对偏心摆动油气混输泵的动力学特性进行分析研究，建立了主要部件的动力学数学模型。

1 基本结构与原理

如图1所示，偏心摆动油气混输泵主要由壳体、油缸、摆轴、滑板等构成。摆轴偏心置于油缸内，且摆轴外表面和油缸内表面始终相切于一点，由此形成了混输泵的月牙形工作腔。滑板一端嵌入壳体的滑板槽内，圆头端与摆轴相连，这样就将工作腔分隔为吸油腔和排油腔。吸油口和排油口分别与吸油腔和排油腔连通。偏心曲轴与摆轴通过角接触轴承相连。泵工作时，偏心曲轴顺时针转动，套在偏心曲轴上的摆轴受到滑板的牵制，使摆轴在油缸中以往复摆动的方式进行容积变化。随着偏心曲轴的旋转，吸油腔的容积不断增大、形成真空，工作介质通过油缸上的吸油口不断进入吸油腔。与此同时，滑板另一侧排油腔的容积不断减小，工作介质通过排油口排出，进而完成吸油、排油过程。

图1 偏心摆动油气混输泵结构示意图

泵工作腔的变化类似于滚动活塞式压缩机工作腔的变化。滑板单侧的工作腔需要偏心曲轴旋转2周才能完成1次吸油、排油过程，但泵的吸油和排油是同时进行的，故泵的偏心曲轴旋转1周就能完成1次工作过程。由于滑板的宽度对于整个油缸而言可以忽略不计，故不考虑滑板的宽度，则泵的工作腔的容积为

(1)

式中，φ为转角；H为摆轴轴向高度；R为油缸半径；r为摆轴半径；e为偏心距。

2 运动与受力模型

2.1 运动学分析

偏心摆动油气混输泵的结构类似于曲柄滑块机构，视滑板为刚体，则滑板任何一点的运动即可代表滑板的运动。由图2可知，滑板在滑板槽中做竖直往复运动，根据速度矢量关系，可得滑板的运动方程：

l=e(1-cosφ)+eεsin2φ/2

(2)

ε=e/r

式中，l为滑板伸出长度，竖直向下为正。

图2 摆轴速度示意图

由式(2)可以看出，φ=0或2π时，l为最小值0；φ=π时，l为最大值2e。对式(2)分别进行一阶、二阶求导，可得滑板运动的速度及加速度。

摆轴同时受到偏心曲轴和滑板的约束，在油缸中做平面运动，摆轴的运动由绕油缸中心的转动(角速度为ω)和以绕自身中心的摆动(角速度为ωp)两部分组成。

如图2所示，选取油缸中心O点处且过滑板中心线的坐标系XOY为定坐标系，过摆轴中心O1点处的坐标系X1O1Y1为动坐标系。滑板圆头端与摆轴在A点处铰接。假定滑板是在平面内竖直运动的刚体，故滑板的速度与摆轴在A点处的速度相等，摆轴在A点处绝对速度为

va=vv

(3)

式中，va为摆轴上A点的速度；vv为滑板的速度。

动坐标系的牵连运动为转动，故摆轴A点处的牵连速度方向为垂直于OO1、沿偏心曲轴的旋转方向。牵连速度的大小为

ve=eω

(4)

式中，ω为偏心曲轴的角速度，ω=nπ/30；n为转速。

动点A相对于动坐标系的相对运动为转动，故摆轴在A点处的相对速度为

vr=(r-r0)ωp

(5)

式中，r0为滑板圆头端的半径。

综上所述，根据速度矢量关系，可得

(6)

故可求得摆轴绕自身旋转中心的角速度(逆时针为正)：

(7)

摆轴绕自身旋转中心的角加速度为

β=dωp/dt

(8)

2.2 动力学分析

由于滑板的重力和其他接触力相比是个小量，故忽略滑板的重力。图3给出了作用在滑板上的所有力：与摆轴间的法向约束力Fn和切向约束力Ft；与滑板槽间的约束力FR1、FR2及其相应的摩擦力Ff1和Ff2；滑板的惯性力FIv以及高-低压工作腔压差作用力Fpb。为了简化计算，近似认为滑板两侧间隙内的压力相互抵消，忽略滑板在滑板槽中所受到的润滑油压力。

图3 滑块受力分析

滑板的圆头端嵌入摆轴，摆轴的圆心和滑板圆头端的圆心构成的连心线与滑板中心线之间的夹角为α。由图3所示的几何关系可得

(9)

滑板的惯性力为

FIv=-mvav

(10)

式中，mv为滑板的质量;av为滑板的加速度。

滑板伸到油缸内的部分承受的压差力为

Fpb=Bl(pc-pd)

(11)

式中,B为滑板厚度；pc为出口压力；pd为入口压力。

滑板受到滑板槽的摩擦力为

(12)

式中，μs为滑板槽的摩擦因数，μs=0.2。

摆轴在油缸中做带微量滑动的滚动，故忽略摆轴与油缸断面的摩擦力矩和摆轴与油缸内壁面的摩擦力矩。根据摆轴的运动微分方程，可得滑板受到的切向约束力：

(13)

式中，MJZ为摆轴所受到的惯性力矩，大小为摆轴绕其轴心的转动惯量与角加速度的乘积；Mc为摆轴与偏心曲轴间的摩擦力矩。

通过上述分析，运用达朗贝尔原理对滑板的质心建立力和力矩方程组：

Fpb-FR1+FR2+Fnsinα-Ftcosα=0

(14)

Ff1+Ff2+Fncosα-Ftsinα-FIv=0

(15)

(Ff1-Ff2)B-FR1(l0-2l)-FR1l0+Fpb(l0-l)+

Fnl0sinα-Ftl0cosα=0

(16)

式中，l0为滑板的长度。

求解式(14)～式(16)，可得在任意φ下Fn、FR1、FR2、Ff1、Ff2的值。

摆轴除了受到滑板的法向约束力Fn和切向约束力Ft，还受到作用在摆轴上的工作介质的压差作用力Fpg、旋转惯性力FIp、与偏心曲轴之间的摩擦力矩Mc,如图4所示。

图4 摆轴受到工作介质的压差作用力

假定混输泵内的流动模型为均相流模型，当偏心曲轴转过角度φ时，可得

为了简化计算，可以近似假设摆轴与偏心曲轴之间的间隙内存在均匀的油膜，则根据润滑理论可得摆轴与偏心曲轴之间的摩擦力矩Mc：

(18)

式中，Re为偏心曲轴半径；δe为摆轴与偏心曲轴之间的间隙；le为偏心曲轴的长度。

由于忽略了摆轴与油缸端面、内壁间的摩擦力矩，而作用在摆轴的力以及摆轴与偏心曲轴之间的摩擦力矩Mc通过摆轴传递到偏心曲轴上，所以只分析偏心曲轴的受力。

与其他接触力相比，摆轴、角接触轴承的重力可以忽略不计。作用在偏心曲轴上的力有滑板的切向约束力Ft、法向约束力Fn和Fpg，摩擦力矩有与摆轴间的摩擦力矩Mc。忽略其他摩擦力矩，将偏心曲轴上的各力简化到油缸中心O点处，构成了一个径向力F(即偏心曲轴轴承承受的径向载荷)和一个附加力偶矩。将径向力F分解到X、Y轴上可得

(19)

(20)

于是，合力F的大小为

(21)

作用在偏心曲轴上的总阻力矩为

Mz=Mc+Mn+Mpg

(22)

(23)

Mn=eFnsin(φ+α)

(24)

式中，Mpg为Fpg产生的阻力矩；Mn为滑板作用在摆轴上的法向约束力Fn形成的阻力矩。

则混输泵的功率为

(25)

3 数值计算及分析

通过上述对滑板和摆轴的运动及受力分析，建立了相应的数学模型。本文以一台额定流量为6 m3/h的偏心摆动油气混输泵为例，对已建立的数学模型进行数值求解并绘制出相应的曲线，同时对计算结果进行分析。该泵的基本设计参数如下：l0=136 mm，B=20 mm，R=82 mm，r=90 mm，e=8 mm，H=20 mm，r0=7 mm，mv=2.3 kg，Re=42 mm，δe=20 mm，le=136 mm，pc=2.4 MPa，pd=0.1 MPa，n=200 r/min。

由图5可知，偏心曲轴匀速旋转时，滑板速度在0≤φ≤2π内按正弦函数的方式变化，且最高速度仅为0.16 m/s。如图6所示，摆轴的角速度ωp在0≤φ≤2π内按余弦函数的方式变化，且最高角速度为2.26 rad/s。

图5 滑板速度

图6 摆轴角速度

由图7可知，FR1和Fpg在0～2π范围内变化相似，都是先增大、后减小，且在偏心曲轴转到φ=π时达到最大，由此可知滑板的接触力FR1分担了大部分的水平高-低压工作腔压差作用力Fpg。

图7 高-低压差作用力、切向力、约束力

滑板受到摆轴的法相约束力Ft远小于水平高-低压工作腔压差作用力Fpg，主要是因为Ft的大小主要跟摆轴的转动惯量和摆轴绕自身旋转的角加速度有关。

如图8所示，Fn在0≤φ≤2π内是先逐渐增大后减小，在φ=π处改变方向，且与摩擦力Ff1、Ff2的变化规律相似，因为Fn主要受摩擦力Ff1和Ff2的影响，随摩擦力的变化而变化。Fn在φ=π处方向发生变化，主要是因为Ff1和Ff2方向反向。

图8 摩擦力、法向力

由图9可知，偏心曲轴两端的轴承受到的径向力在0～2π内先逐渐增大然后再逐渐减小，在φ=π处取得最大值。由图10可知，阻力矩Mn、Mc与阻力矩Mpg相比很小，可以忽略不计；阻力矩Mpg和总阻力矩Mz的变化规律相似，故影响偏心摆动油气混输泵阻力矩的主要因素是Fpg所产生的阻力矩Mpg。由于偏心曲轴的转速较低，导致泵的摩擦力矩Mc相对Mpg很小，对总阻力矩贡献很小，故可以假定在泵进出口压差较高时，可以忽略各处摩擦对混输泵的影响。Mn在0≤φ≤π范围内先逐渐增大，然后降为0，主要是因为在φ=π时Fn的方向是指向油缸中心处，导致此处的Mn为0。

图9 偏心曲轴的径向力随转角变化的曲线

4 实验研究

为了验证所建立动力学模型的正确性，实验以含少量空气的废机油(油气混输过程中，气液流是不稳定的，从而影响实验结果的精确度)为介质，在混输泵输出口压力变化的条件下进行功率测试。用测得的实验功率和理论功率进行比较，来验证已建立的动力学模型是否正确。

图11所示为偏心摆动油气混输泵的实验台装置，实验台架主要包括液体循环管路和气体管路、管道泵、压缩机，以及测量各种数据的仪器仪

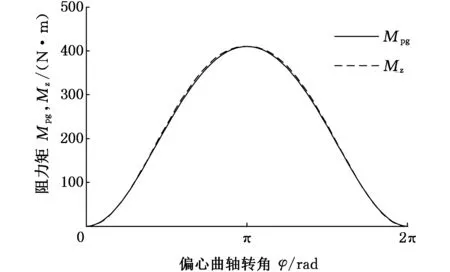
(a)阻力矩Mpg和Mz

(b)阻力矩Mn

表、控制实验的阀门等。其中，防爆变速电机为混输泵提供动力，通过测量与混输泵相连的已知效率的电机的输入功率来确定泵的输入功率。试验泵的额定流量为6 m3/h，额定转速为200 r/min。

实验时，由管道泵提供的废机油和由压缩机提供的空气分别经过各自的管路进入混输泵，经过混输泵加压后进入分液罐，空气被排空，废机油流进储油罐用于再循环。混输泵的输出压力是通过调节混输泵输出管路上的阀门实现的。

混输泵在实验台上进行混输实验时，该泵运行平稳，振动较小，噪声较小，运行时间超过3h，联轴器处的轴承温度从28 ℃升到46 ℃，且能够进行短时间的干转。

图12所示为混输泵实验功率和计算功率的对比曲线。实验功率和计算功率都随着进出口压差的增大而增大，且变化规律相似，进出口压差在1.2～3MPa内时，相对偏差为1%～38.2%，且随着压差的升高而降低。这主要是因为影响样机功

图11 混输泵实验台示意图

率的主要因素不仅是压差，重力和摩擦损耗对功率的影响同样重要，但随着压差的增大，影响样机功率的主要因素是进出口压差，故随着压差的增大,相对偏差变小，计算功率越来越接近实验功率。

图12 混输泵功率随压力的变化

5 结论

(1)在分析混输泵内部关键部件的运动和受力的基础上，建立了偏心摆动油气混输泵的动力学模型，并通过样机的计算得到了一个主轴旋转周期内各种力、力矩的变化曲线。

(2)偏心摆动油气混输泵中的滑板与摆轴连接处的法向约束力Fn较大且发生突变，滑板受到的接触力FR1分担了大部分的水平高-低压工作腔压差作用力Fpb，作用在摆轴上的工作介质的压差作用力Fpg所形成的阻力矩是影响混输泵功率的主要因素。

(3)通过对混输泵进行实验测试，在1.2～3 MPa的工作压力范围内，样机的理论功率和实测功率的相对偏差为1%～38.2%；压差较低时，理论功率和实测功率相对偏差较大，说明影响功率的主要因素不只是压差，故需要进一步分析低压差时重力和摩擦损耗对动力特性的影响。

[1] 杨旭, 屈宗长, 吴裕远. 同步回转式混输泵的工作原理与动力特性研究[J]. 西安交通大学学报, 2010, 44(5): 60-65. Yang Xu , Qu Zongchang, Wu Yuyuan. Working Principle and Dynamic Characteristics of a Synchronal Rotary Multiphase Pump[J]. Journalof Xi’an Jiaotong University, 2010, 44(5): 60-65.

[2] Yang X, Qu Z, Wu Y. Frictional Loss Studies and Experimental Performance of a New Synchronal Rotary Multiphase Pump[J]. Journal of Fluids Engineering, 2011, 133(4): 041303.

[3] Yang X, Qu Z, Hu X, et al. Theoretical and Experimental Performance Analysis of a Synchronal Rotary Multiphase Pump with the Inlet Gas Volume Fractions of 0-0.9[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2012, 226(6): 727-737.

[4] 杨旭, 屈宗长, 束鹏程. 同步回转式压缩机动力分析及计算[J]. 流体机械, 2007, 35(11): 15-20. Yang Xu， Qu Zongchang, Shu Pengcheng.Dynamic Analysis and Calculationon Synchronal Rotary Compressor[J]. Fluid Machinery, 2007, 35(11): 15-20.

[5] Zhou H, Qu Z, Yang H, et al. Dynamic Model and Numerical Simulation for Synchronal Rotary Compressor[J]. Journal of Fluids Engineering, 2009, 131(4): 041102.

(编辑 张 洋)

Research on Dynamic Characteristics of an Eccentric Swing Multiphase Pump

Ji Xiaoke1，2Liang Zheng1

1.Southwest Petroleum University，Chengdu，610500；2.Changqing Oilfield Company，Xi’an，710018

Working principles and structural characteristics of a new eccentric swing multiple pump were described. Motion and dynamics mathematical model of the motion parts of the multiphase pump was established. Numerical calculation was performed for a prototype of motion and dynamics mathematical model. Finally, experiments verified this theory was feasible. The results show that drag torque which is formed by the differential pressure forces on the swing-axle is the main influence on the shaft power pump. In the import and export pressure ranges of 1.2～3MPa, the deviation of the power input tested and calculated is in the ranges of 1%～38.2%.

eccentric swing multiphase pump; vane; swing-axle; dynamics

2015-03-06

TE977

10.3969/j.issn.1004-132X.2016.21.009

吉效科，男，1976年生。西南石油大学机电工程学院博士研究生，长庆油田公司设备管理处高级工程师。主要研究方向为石油矿场机械。发表论文26篇，出版著作4部。梁 政，男，1960年生。西南石油大学机电工程学院教授、博士研究生导师。