基于组合赋权的机床加工工艺参数多目标综合决策方法

邓朝晖 孟慧娟 张 华 万林林

湖南科技大学难加工材料高效精密加工湖南省重点实验室，湘潭，411201



基于组合赋权的机床加工工艺参数多目标综合决策方法

邓朝晖 孟慧娟 张 华 万林林

湖南科技大学难加工材料高效精密加工湖南省重点实验室，湘潭，411201

针对机床加工过程的复杂性，提出了考虑传统决策指标和资源环境属性决策指标的多目标决策方法。依据层次分析法和指标相关性的指标权重确定方法对各指标进行主客观组合赋权，采用TOPSIS设定正负理想序列，分别采用欧氏距离法和灰色关联法对各实验组(工艺参数组合)进行排序，剔除两种方法下排序差异大的方案，得到了折中的最优工艺参数。最后，以平面磨床磨削实验为例对该方法进行了论证。

多目标决策；组合赋权；灰色关联法；欧氏距离法；TOPSIS

0 引言

机床是机械制造业的重要工具，在为人类创造财富的同时也消耗了大量的资源能源，造成了严重的环境污染[1]。通过对机床加工工艺参数的决策优化，可有效降低生产加工过程中的资源消耗，减少污染排放，提高生产效益和加工质量，既满足企业的发展需要，又对我国机床制造业也有着重要的工程应用价值。

近年来，国内外学者对机床加工过程中工艺方案的决策和优选已经进行了较多的研究。Bennett等[2]提出的产品工艺决策模型不仅考虑了废物减排，还考虑了能量消耗。Chen等[3]采用神经网络法对切削加工工艺参数进行多目标优化，不仅降低加工成本，并且提高加工表面的质量。江志刚等[4-5]建立生产过程输入输出多目标决策模型，基于该模型阐述了决策指标和工艺参数的关系，并构建了决策模型。曹华军等[6]采用了层次分析法(analytic hierarchy process, AHP)进行了主观赋权，建立了综合考虑资源消耗和环境影响的多目标决策模型。曹杰等[7]从资源环境属性等方面建立了绿色制造工艺评价体系的层次结构模型，并采用多目标决策逼近理想解法对各工艺方案进行排序。伍晓榕等[8]运用决策试验与评价实验室方法进行绿色工艺参数决策，获得了考虑决策者主观偏好的绿色工艺参数。Hanafi等[9]利用灰色关联理论对切削工艺参数进行优化，以实现最低功耗和最佳表面质量。Yan等[10]以表面粗糙度、材料去除率和能源消耗为优化目标，提出了一种基于加权灰色关联分析和响应面法的多目标优化方法，并进行了实验验证。李郝林等[11]以平面磨床磨削加工粗糙度和平面度为优化目标，通过灰色关联度排序，从而决定最优的工艺参数。顾丰[12]采用信噪比和灰色关联算法，对微电火花加工工艺参数进行决策优化，得到了多项输出指标要求下的最优工艺参数。赵茂俞等[13]针对冲压工艺设计正交实验，利用灰色系统理论来计算成形质量与各指标的灰色关联度，从而优选最佳工艺参数，最终进行生产应用，应用结果表明成形质量明显提高。

以上对机床加工工艺进行多目标决策的研究存在以下不足之处：①决策指标只考虑了资源环境属性，或者只考虑了生产效益和加工质量；②决策指标的权重大多为等重或者主观权重，导致决策结果出现较大的主观随意性；③采用灰色关联进行机床加工工艺的决策时，设定的参考序列只考虑正理想序列的一致度，没有考虑和负理想序列的相异度，并且仅仅采用灰色关联算法进行决策，没有与其他决策方法进行对比，无法判断最终决策的最优工艺是否有误。

以上研究的不足之处，可能导致研究结果出现误差。对机床工艺参数进行决策研究时，全面考虑决策指标，并采用多种方法对决策结果进行对比分析以提高决策结果正确性，是很有必要的。本文的决策指标系统不仅要考虑机床生产过程中的资源消耗和排放，还要考虑生产效率和加工质量等传统指标。此外，决策指标权重向量的设定不仅要考虑决策者的主观偏好，还考虑决策指标间的相关性和差异性。本文采用灰色关联算法进行决策的同时，还引入欧氏距离算法，可以剔除两种决策方法下排序争议比较大的实验方案，得到折中的最佳工艺参数，从而达到减小决策误差，提高决策正确率的目的。最终通过平面磨床磨削工艺参数的决策实验进行实验验证。

1 加工工艺IPO模型

机械制造是一个复杂的加工过程，涉及资源消耗、加工质量和污染排放等活动。图1所示为机械制造系统切削工艺IPO模型。

通过对图1所示切削工艺IPO模型的分析可知，零件加工消耗了资源和能源，产生了噪声和粉尘，生产效率与加工质量直接影响到企业效益和产品合格率，故在机床加工工艺的决策中，决策指标的设定不仅要考虑资源消耗和排放，还要考虑生产效率和加工质量等传统指标。

2 组合赋权

机床加工工艺多目标决策研究中，决策指标权重的设定具有非常重要的意义，它反映了各个决策指标在决策中的地位和重要度，直接影响最终的决策结果。根据赋权方法的不同，权重可以分为主观权重和客观权重[14]。主观权重是专家以及决策者根据以往的经验直接给指标设定的权重。AHP具有分析思路清晰、分析时使用数据较少的特点，适用于复杂的机床加工工艺决策问题，故本文采用AHP确定决策指标的主观权重yj(由于层次分析法在应用比较普遍，本文省略AHP具体计算过程)[15]。客观权重确定方法可以充分利用实际采集的实验数据之间的规律，不受人为主观因素影响，具有一定的灵活性。客观赋权法中，指标相关性的指标权重确定 (criteria importance through inter-criteria correlation, CRITIC) 法不仅考虑了决策指标差异性，还考虑了各指标之间的冲突性，由于机床加工过程中的决策指标间具有差异性和相关性，故CRITIC法更适用于机床加工。

2.1 CRITIC法

CRITIC法是由Diakoulaki提出的一种客观权重赋权法。它以两个因素为基础进行权重设定：(1)对比强度表示同一指标各个评价方案取值差距的大小，以标准差的形式来表现，即标准差的大小表明了同一指标内各方案的取值差距的大小，标准差越大，各方案的取值差距越大；(2)决策指标之间的冲突性以指标之间的相关性为基础，若两个指标之间具有较强的正相关，则说明两个指标冲突性较低[16-17]。

(1)首先对收集的实验数据构建决策矩阵X=[xij]m×n，i=1，2，…，m；j=1，2，…，n。其中，m为方案数，n为决策指标数。

(2)用标准方差法对决策矩阵进行标准化处理：

(1)

(3)计算对比强度sj：

(2)

(4)计算决策指标之间的冲突性指标(反映第j个指标和其他指标之间的冲突性)cj：

(3)

(4)

式中,rij为指标间的相关系数。

(5)计算客观权重θj：

(5)

2.2 主客观权重综合赋权

主客观组合赋权既可以尽量减少决策者的主观随意性，又可以弥补客观权重确定方法的不足。利用变异系数来计算决策指标的组合权重，可以克服决策指标权重分配均衡化的缺陷，使组合权重的赋值更为客观合理[18-19]。具体过程如下：

wj=αθj+(1-α)γj

(6)

(7)

(8)

式中，GAHP为层次分析法各指标权重的变异系数；P1，P2，…，Pn依次表示γ(k)从小到大的权重值。

3 机床加工工艺参数决策

3.1 理想序列

(1)计算加权标准化矩阵：

U=[uij]m×n=[wjyij]m×n

(9)

确定正负理想参考序列[21]：

(10)

(11)

其中，U+为正理想序列，其中的指标是高优指标，即指决策指标值越大越好；U-为负理想序列，其中的指标是低优指标，即指决策指标值越小越好。比如加工时间越短越好，为低优指标，故正理想序列U+取最小值min uij，负理想序列U-取最大值max uij。

3.2 决策方法

对于机床加工系统而言，其输出的指标间存在较强的非线性关系，采用数理统计方法很难表达出来决策指标间的非线性关系。利用灰色关联和欧氏距离法通过对数据序列整体的比较，可以方便快捷地得出最佳工艺参数[20,22]。

(1)利用欧氏距离计算参考序列i和理想序列的相对贴近度。

到正理想序列的距离：

(12)

式中，ui(j)为加权标准化矩阵第i行第j列对应的数值；u+(j)为正理想参考序列第j列数值。

到负理想序列的距离：

(13)

式中，u-(j)为负理想参考序列第j列数值。

欧氏距离贴近度：

(14)

归一化的欧氏距离贴近度：

(15)

(2)利用灰色关联度计算方案i相对贴近度和综合贴近度。

正关联系数：

(16)

负关联系数：

(17)

灰色关联贴近度：

(18)

灰色关联贴近度归一化处理：

(19)

最终获得的综合贴近度：

Ci=(Di+Ri)/2

(20)

本文方法除了可以得到最佳工艺参数以外，还可以对机床加工工艺参数的影响度进行计算排序，计算方法在应用实例中进行说明。

3.3 实现步骤

综合以上理论可得机床加工工艺参数决策流程图(图2),具体实现步骤如下：

图2 机床加工工艺决策流程图

(1)根据机床实际加工情况建立IPO模型图，并进行机床加工的资源环境属性分析，确定机床加工过程的决策指标体系。

(2)确定对决策指标的影响因素以及各影响因素水平值，设计正交试验，进行实验数据的收集和预处理，得到标准化的决策矩阵。

(3)采用层次分析法和CRITIC法对决策指标进行主客观组合赋权，并利用所得权重对标准化决策矩阵进行加权，得到加权标准化决策矩阵，从而确定正负理想参考序列。

(4)分别采用灰色关联法和欧氏距离法计算加权标准化矩阵和理想参考序列的贴近度，并进行排序，剔除两种方法下排序差异比较大的方案，并对其余排序基本一致的方案进行综合排序。

4 应用实例

磨削加工是一种精密加工方法，在加工过程中消耗了大量的资源和能源，产生的噪声、粉尘等对环境产生了严重的影响[23]。建立平面磨削加工过程IPO模型图，如图3所示。

平面磨削决策指标的设定不仅要考虑其生产效益、生产成本，还有考虑其环境影响。磨削过程中,磨削力直接影响着磨削热的产生，并进一步影响砂轮的磨损、耐用度及工件已加工表面的质量，所以本文将磨削力作为了一个重要的决策指标。由于磨削加工属于精密加工，产生的粉尘较少，采用粉尘测量仪测出的粉尘浓度变化很小，所以本文不将粉尘作为决策指标。最终确定的决策目标为能耗、粗糙度、加工时间、噪声和磨削力。

图3 平面磨削加工IPO模型

4.1 实验研究

本文以工艺参数的优选为目的，根据相关方法和理论，在数控平面磨床上进行实验，实验中所采用的加工设备如表1所示。

表1 实验设备表

实验中考虑如下工艺参数：进给速度vw、砂轮线速度vs、磨削深度ap。设计三因素四水平L16(43)正交试验。实验中，定工件台行程取固定值0.3 m，磨削总厚度Z=0.6 mm，分别测量16组工艺实验的磨削功率、生产时间、噪声、磨削力和粗糙度。表2所示为平面磨削工艺实验方案和决策指标实验数据。对实验数据进行分析处理，优选最佳工艺参数，可以达到减少能源消耗、噪声，提高生产效率和加工零件表面质量的目的。

表2 实验工艺参数和测量结果

4.2 实验数据处理

对表2中采集到的实验数据构建决策矩阵：

(21)

对式(21)进行标准化处理：

(22)

4.3 决策指标主客观组合赋权

(1)利用层次分析法确定主观权重：

(γ1，γ2，…，γ5)=

(0.2452,0.5042,0.1024,0.1024,0.0459)

(2)利用CRITIC确定客观权重：

对比强度为

(S1，S2，…，S5)=

(0.1671,0.1627,0.0467,0.0834,0.0069)

冲突性指标为

(C1，C2，…，C5)=

(4.6538,4.6561,4.4734,4.1597,4.6098)

客观权重为

(θ1，θ2，…，θ5)=

(0.3663,0.3569,0.0984,0.1634,0.0150)

(3)计算可知变异系数α=0.4，则组合权重为

(w1，w2，…，w5)=

(0.2936,0.4453,0.1008,0.1268,0.0335)

4.4 平面磨削工艺参数决策

(1)对式 (22)进行加权，得

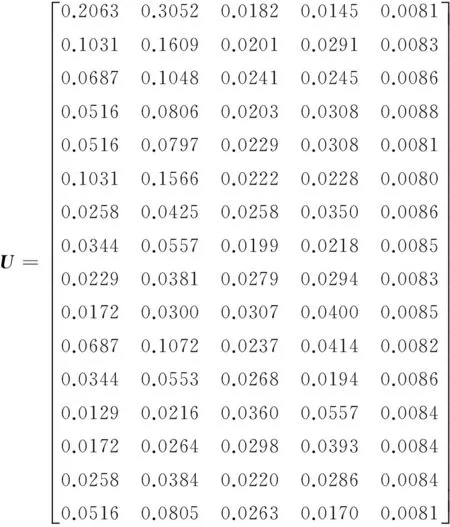
(23)

(2)确定正负理想序列、正理想序列：

U+=[0.0129 0.0216 0.0182 0.0145 0.0080]

U-=[0.2063 0.3052 0.0360 0.0557 0.0088]

(3)计算各方案到正负理想序列的欧氏距离：

(4)计算各方案与正负理想序列的灰色关联度：

(R1，R2，…，R16)=(0.4367,0.4421,0.4508,0.4664,

0.4665,0.4402,0.5197,0.4813,0.5314,0.5319,

0.4624,0.4850,0.5274,0.5244,0.5081,0.4588)

(5)计算综合贴近度并排序，结果如表3所示。

(6)计算机床工艺参数综合影响度，并排序。

表3 平面磨削工艺实验方案贴近度排序

本文方法除了可以得到最佳工艺参数以外，还可以得到磨削工艺参数每一水平的平均贴近度，计算方法如下：将正交序列中的贴近度值依照参数水平分组，计算每组贴近度的平均值，获得各参数水平的平均贴近度。例如，进给速度为1 m/min时的灰色关联理想贴近度平均值γ11=(0.027 73+0.048 24+0.058 17+ 0.063 09)/4=0.0493。平面磨削每个参数因素的每个水平都可采用同样的方法来计算平均贴近度，如表4所示。

表4 各工艺参数综合影响度排序

4.5 平面磨削工艺实验分析

从表3可以看出，不管是采用灰色关联法还是欧氏距离法，其贴近度的排序基本上是一致的。但对于第15组实验，采用灰色关联法进行排序时为1，采用欧氏距离法排序为5；对于第10组实验，采用灰色关联法进行排序时为4，采用欧氏距离法排序为1，说明第15组实验和第10组实验存在着很大的争议。第9组实验两种方法下的排序都是2，其综合排序为1，故第9组实验是考虑能耗、表面粗糙度、磨削力、加工时间和噪声的折中最佳工艺参数。从表4可以看出，对各评估指标影响最大的参数是进给速度，其次是磨削深度，砂轮线速度的影响因程度最小。为了使输出参数更好地逼近理想值，调整进给速度和磨削深度可以达到更好的效果。

将灰色关联和欧氏距离应用于多目标决策的研究已经比较成熟，但是国内外学者一般都采用其中一种方法进行决策，无法直观判断决策结果是否存在误差。本文采用了灰色关联和欧氏距离两种决策方法对机床加工实验方案进行了排序，可以剔除争议性比较大的实验方案，获得折中的最佳工艺参数，大大减小了决策误差，提高了决策结果的正确度。并且本文提出采用CRITIC法计算指标间的对比强度和冲突性，从而客观考虑了决策指标间的差异性和相关性，从而削弱了决策者的主观随意性，使得决策结果更为合理有效。

5 结论

(1)采用灰色关联和欧氏距离两种算法分别对各实验方案进行了排序，剔除了两种方法下排序争议比较大的实验方案，对其余实验方案进行了排序，获得了一组折中的最优工艺参数，提高了决策结果的准确性。

(2)通过各工艺参数因素同一水平下的平均灰色关联理想值分析，找到对评估指标影响最大的工艺参数为进给速度，其次是磨削深度、砂轮线速度。

(3)机床加工过程是一个多输入、多输出系统，具有非线性和强耦合关系，本文采用CRITIC法进行客观赋权，并在综合考虑数据间相关性和冲突性的基础上，结合层次分析法进行主客观组合赋权，使决策指标的权重设定更为合理。

(4)本文以平面磨削加工为例，对磨削加工工艺参数进行优选决策，有助于提高机床加工的绿色度。本文所采用的方法，同样适用于加工工艺路线的决策优选，对提高企业生产效益有很大的作用，并且可以通过MATLAB分析得出结果，有较强的推广使用价值。

[1] 张华.绿色制造系统工程理论与实践[M].北京：北京科学出版社,2013.

[2] Bennett D P, Yano C A. A Decomposition Appr-oach for an Equipment Selection and Multiple Product Routing Problem Incorporating Environmental Factors[J].European Journal of Operational Research,2004,156(3):643-664.

[3] Chen L P, Jian C, Gang C.Multi-objective Optimization of Cutting Parameters in Sculptured Parts Machining Based on Neural Network[J].Journal of Intelligent Manufacturing,2015,26(5):891-898.

[4] 江志刚,张华,肖明.面向绿色制造的生产过程多目标集成决策模型及应用[J].机械工程学报,2008, 44(4):41-46. Jiang Zhigang, Zhang Hua, Xiao Ming. Multi-objective Integrating Decision-making Model and Its Application of Production Process for Green Manufacturing[J]. Journal of Mechanical Engineering,2008,44(4):41-46.

[5] 江志刚,张华. 绿色制造企业生产过程多目标集成决策指标体系研究[J].机械设计与制造,2008(8):232-234. Jiang Zhigang, Zhang Hua. Study on Index System of Multi-objective Decision-making for Production Process Oriented Green Manufacturing Enterprise[J]. Machin-ery Design and Manufacture,2008(8):232-234.

[6] 曹华军,刘飞,何彦,等.面向绿色制造的机床设备选择模型及其应用[J].机械工程学报,2004,40(3):26-30. Cao Huajun, Liu Fei, He Yan, et al. Machine Tool Selection Model and It Application for Green Manufacturing[J]. Journal of Mechanical Engineering, 2004, 40(3):26-30.

[7] 曹杰, 易红. 绿色产品制造工艺方案的研究[J]. 机械工程学报,2002,38(7):126-130. Cao Jie, Yi Hong. Studying Scheme of Green Product Manufacturing Process[J]. Journal of Mechanical Engineering, 2002,38(7):126-130.

[8] 伍晓榕,张树有,裘乐淼, 等. 面向绿色制造的加工工艺参数决策方法及应用[J].机械工程学报,2013, 49(7):91-100. Wu Xiaorong, Zhang Shuyou, Qiu Lemiao, et al. Decision Making Method of Process Parameters Selection for Green Manufacturing Based on a DEMATEL-VIKOR Algorithm[J]. Journal of Mechanical Engineering, 2013, 49(7):91-100.

[9] Hanafi I,Khamlichi A, Cabrera F M, et al. Optimization of Cutting Conditions for Sustainable Machining of PEEK-CF30 Using TiN Tools[J]. Journal of Cleaner Production, 2012,33(8):1-9.

[10] Yan J, Li L. Multi-objective Optimization of Milling Parameters-the Trade-offs between Energy, Product-ion Rate and Cutting Quality[J]. Journal of Cleaner Production, 2013,52(4):462-471.

[11] 李郝林,王健.基于灰色关联分析的平面磨削工艺参数优化[J].中国机械工程,2011,22(6):631-635. Li Haolin, Wang Jiang. Determination of Optimum Parameters in Plane Grinding by Using Grey Relational Analysis[J]. China Mechanical Engineering, 2011, 22(6):631-635.

[12] 顾丰.电火花微小孔加工工艺参数优化及建模的研究[D].大连:大连理工大学,2006.

[13] 赵茂俞,薛克敏,李萍.多目标质量的覆盖件成形工艺参数优化[J].机械工程学报,2009,45(8):276-282. Zhao Maoyu, Xue Kemin, Li Ping. Auto Panel Forming Process Parameters Optimization of Multi-objective Quality[J]. Journal of Mechanical Engineering, 2009, 45(8): 276-282.

[14] 杜栋.现代综合评价方法与案例[M].北京:清华大学出版社,2008.

[15] 赵焕臣,许树柏.层次分析法[M].北京:北京科学出版社,1986.

[16] 王昆.三种客观权重赋权法的比较分析[J].技术经济与管理研究,2008(6):48-49. Wang Kun. Three Kinds of Objective Weight Method of Comparative Analysis[J].Technoeconomics & Management Research, 2008(6):48-49.

[17] Diakoulaki D, Mavortas G, Papayannakis L. Determining Objective Weights in Multiple Crireria Problems: The CRITIC Method[J].Computer Ops.,1995, 22: 763-770.

[18] 时光新,王其昌,刘建强.变异系数法在小流域治理效益评价中的应用[J].水土保持通报,2000,20(6):47. Shi Guangxin, Wang Qichang, Liu Jianqiang. Application of Variation Coefficient Method in the Evaluation of Management Benefit of Small Watershed[J]. Bulletin of Soil and Water Conservation, 2000, 20(6):47.

[19] 席荣宾,黄鹏,赖雪梅,等.组合赋权法确定权重的方法探讨[J].中国集体经济,2010(7):75-76. Xi Rongbing, Huang Peng, Lai Xuemei, et al. Study on the Method to Determine the Combina-tion Weight[J]. China Collective Economy,2010(7):75-76.

[20] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社, 2002.

[21] 卢方元. 一种改进的TOPSIS法[J]. 统计与决策, 2003(3):78-79. Lu Fangyuan. A Kind of Improved TOPSIS Met-hod[J]. Statistics and Decision, 2003(3):78-79.

[22] 张尧庭. 多元统计分析引论[M]. 武汉：武汉大学出版社, 2013.

[23] 修世超,冯强.绿色磨削实现技术及其理论框架的构建[J].制造技术与机床,2008(10):28-32. Xiu Shichao, Feng Qiang. Frame of Theory and Achieving Technology for Green Grinding Process[J].Manufacturing Technology & Machine Tool, 2008(10):28-32.

(编辑 张 洋)

A Multi-objective Comprehensive Decision Method for Machine Tool Machining Process Parameters Based on Combination Weight

Deng Zhaohui Meng Huijuan Zhang Hua Wan Linlin

Hunan Province Key Laboratory of High Efficiency and Precision Machining of Difficult-to-machine Material,Hunan University of Science and Technology,Xiangtan, Hunan,411201

Considering the complexity of machining processes, a multi-objective decision method was proposed, which took the traditional decision-making factors and environmental impact target into account. The combination weight were determined by analytic hierarchy process and criteria importance through inter-criteria correlation, and the positive and negative reference sequences were set by TOPSIS. Grey correlation and Euclidean distance were used to sort each experimental group(combination of process parameters). The groups which had a significant difference under the two methods were rejected, and the compromise optimal parameters might be obtained. Finally, the method was verified by surface grinding experiments.

multi-objective decision; combination weight; grey correlation; Euclidean distance; technique for order preference by similarity to ideal solution (TOPSIS)

2015-12-21

国家高技术研究发展计划(863计划)资助项目(2014AA041504)

10.3969/j.issn.1004-132X.2016.21.011

邓朝晖，男，1968年生。湖南科技大学机电工程学院教授、博士研究生导师。主要研究方向为高效精密智能制造和绿色制造技术。发表论文50余篇。孟慧娟，女，1990年生。湖南科技大学机电工程学院硕士研究生。张 华，男，1976年生。湖南科技大学机电工程学院博士研究生。万林林，男，1984年生，湖南科技大学机电工程学院讲师。

图书分类号：TH16