浮动平底推杆共轭凸轮机构的狭义/广义第Ⅱ类机构综合问题

2016-12-24吴秋平李延平

中国机械工程 2016年21期

关键词：返程滚子推杆

常勇吴秋平李延平

集美大学，厦门，361021

浮动平底推杆共轭凸轮机构的狭义/广义第Ⅱ类机构综合问题

常勇吴秋平李延平

集美大学，厦门，361021

浮动平底推杆；共轭凸轮机构；机构综合；瞬时一维直线区段；最小跨距

0 引言

文献[1]以高速印刷机上的机构为研究对象，归纳、概括和提出Ⅰ类、Ⅱ类机构综合问题，通过引入“浮动数轴”、“瞬时区间套”和“整程区间套”等概念，解决了力锁合浮动滚子推杆盘形凸轮机构的第Ⅱ类尺寸综合问题。文献[2]以高速印刷机上的机构为研究对象，引入“往程、返程”和“向径标刻线”等概念，解决了浮动滚子推杆共轭、槽道和等径凸轮机构的第Ⅱ类尺寸综合问题。文献[3]通过引入“瞬时/整程选择区域”和“最经济搜索带域”等概念，解决了浮动滚子推杆盘形凸轮机构的广义第Ⅱ类尺寸综合问题。文献[4]应用“支撑函数法”，获得了浮动平底推杆力锁合盘形凸轮机构的凸轮轮廓曲率半径、外凸性判据、参数方程、周长和面积等的通用计算公式。文献[5]将滚子演化为平底，引入“斜交浮动系”、“支撑函数法”、“瞬时一维直线区段”和“瞬时区间套”等概念，解决了浮动平底推杆力锁合盘形凸轮机构的狭义、广义第Ⅱ类尺寸综合问题。

平底较之滚子，在改善润滑受力、减小凸轮副力和降低功耗方面，具有显著优越性。共轭凸轮机构具有运动精度高、抗冲击好、寿命长和适用于高速场合等诸多优点。因此，研究浮动平底推杆共轭凸轮机构的第Ⅱ类尺寸综合问题，具有机构学理论研究和工程应用的重要意义。

1 对象机构的第Ⅱ类尺寸综合问题

图1所示为高速印刷机送纸机构[1]的演化型——浮动平底推杆共轭凸轮机构。机构运动时，主凸轮1与主平底G 在K点接触，副凸轮1′与副平底G′ 在K′点接触，G和G′位于凸轮轴心O1两侧。

(a)凸轮顺时针转动

(b)凸轮逆时针转动

2 对象机构的狭义第Ⅱ类综合问题

2.1 满足α≤[α]机构解的存在性(态)

为清楚阐述问题，引入如下概念[2]。

(1)往程/返程。往程，即输出件摇杆4的角位移从零增大到幅值的行程；返程，即输出件摇杆4的角位移从幅值减小到零的行程。往程时，主凸轮1接触主平底G，驱动机构运动，副凸轮1′、副平底G′起锁合作用。返程时，副凸轮1′接触副平底G′，驱动机构运动，主凸轮1、主平底G起锁合作用。 “往程/推程”与“返程/回程”含义不同，详见文献[2]。

(2)F型机构[6]:往程平底远离凸轮轴心，返程平底靠近凸轮轴心的机构。

(3)P型机构[6]:往程平底靠近凸轮轴心，返程平底远离凸轮轴心的机构。

通常，推程许用压力角[α]的取值范围是30°～40°，回程许用压力角[αr]的取值范围是70°～80°。

2.1.1 凸轮顺时针转动时的主凸轮机构(F型机构)

(1)推程。据文献[5]中的图2a，推程任一瞬时P21皆位于O1O2的上方。文献[5]中的图2、图3和图5，以及式(15)～式(42)具有通用性。若文献[7]式(37)或式(40)成立，则满足α≤[α]条件的“推程区间套”:

v∈[vC1max，vC2min]

(1)

vC1max、vC2min的求解，详见文献[5]。

(2)回程。据文献[5]，“推程区间套”通常嵌套在“回程区间套”中，故满足前者，自然满足后者。

(3)整程。综合推程、回程可知，“推程区间套”即“整程区间套”,如图2所示。

(a) 不存在机构解

(b) 存在唯一机构解

(d) uK-θ1曲线

2.1.2 凸轮顺时针转动时的副凸轮机构(P型机构)

2.1.2.1 推程(返程)

图3 副凸轮机构满足α≤[α]解集的求解原理

(2)

(3)

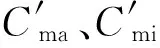
据与文献[7]式(10)，有0°<σ′<180°。

(a) 前半区段

(b) 后半区段

(4)

(5)

(1)推程前半区段。据图4a中几何关系，有

(6)

其中，s2r(θ1)为返程s2随凸轮转角θ1的变化规律，η为行程系数，推程η=1，回程η=-1。

(7)

和

防治方法：一是选用无病种薯，播种前用40%福尔马林120倍液浸种4分钟。二是多施有机肥或绿肥，可抑制发病。三是与葫芦科、豆科、百合科蔬菜进行5年以上轮作。四是选择保水好的菜地种植，结薯期遇干旱应及时浇水。

(8)

可得

(9)

s2r(θ1)+l21r(θ1)cot σ′

(10)

C1在浮动坐标系v轴上的坐标分量为

(11)

(2)推程后半区段。据图4b中几何关系、式(6)和

(12)

得

(13)

(14)

将返程规律βr=βr(θ1)代入文献[5]的式(1)～式(9)，用θ40-β代替θ40-βr，即可得到s2r(θ1)、l10r(θ1)和l21r(θ1)。

(a)不存在机构解

(b)存在唯一机构解

(c)存在无数机构解

-θ1曲线

2.1.2.2. 回程(返程)

据文献[5]，“推程区间套”通常嵌套在“回程区间套”中，故满足前者，自然满足后者。

2.1.2.3 整程

综合推程、回程，“推程区间套”即“整程区间套”。

凸轮逆时针转动情况下，“整程区间套”求解过程与顺时针情况同理，从略。

2.2 满足ρ>0条件机构解的存在性(态)

2.2.1 凸轮顺时针转动

主凸轮机构(F型机构)求解过程详见文献[5]。副凸轮机构(P型机构)求解过程如下。

(15)

A=l4[l4+l0cos(θ40-βr)]

图6 副凸轮机构-支撑函数、方向角分析提取

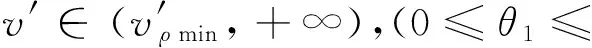
(16)

(17)

2.2.2 凸轮逆时针转动

凸轮逆时针转动情况下，“整程区间套”求解过程与顺时针情况同理，从略。

2.3 满足α≤[α]∩ρ>0条件机构解的存在性

2.3.1 凸轮顺时针转动

(1)主平底线G的许用范围见文献[5]。

图7 存在无数解的情形

(3)主平底G工作段及理论/实际长度的确定详见文献[5]。

(4)副平底G′。设副平底所在方位线G′的在“浮动坐标轴”v方向上的分量为v0，平底线与连杆线交点为O″2，则过O″2点建坐标轴O″2u″(O″2u″平行于O2u′)，如图8所示。O″2u″、O2u′两坐标轴间关系为

(18)

图8 [u″Kmin,u″Kmax]的求解

副平底G′工作段，即副凸轮、副平底接触点的范围为(uK)″∈[u″Kmin, u″Kmax]，副平底G′的理论长度l′=|u″Kmax-u″Kmin|，副平底G′的实际长度：l′+5≤L′≤l′+7,单位mm。

2.3.2 凸轮逆时针转动

凸轮逆时针转动情况下，主、副平底工作段及理论/实际长度的求解过程与顺时针情况同理，从略。

3 主副平底夹角解域等的重要结论

3.1 凸轮顺时针转动

主凸轮机构(F型机构)的结论详见文献[5]。这里研究副凸轮机构(P型机构)。满足α≤[α]∩ρ>0条件时，σ′的取值范围：90°-[α]<σ′<90°+[α]。

(a)v′-σ′曲线

曲线

(c)l′-σ′曲线

3.2 凸轮逆时针转动

凸轮逆时针转动情况下，上述物理量的求解过程与顺时针情况同理，从略。

2.1节研究解决了对象机构的狭义第Ⅱ类综合问题，2.2节研究解决了浮对象机构的广义第Ⅱ类综合问题。

4 共轭凸轮机构的重要结论

4.1 σ≠σ′情形

4.2 σ=σ′情形

σ=σ′即特殊情形。出于习惯，工程实际中常取用G∥G′机构形态，即主副平底平行，如图10所示。

图10 浮动平底推杆共轭凸轮机构(σ=σ′)

如图10所示，主副平底的跨距(衡量机构尺寸紧凑性的重要评价指标)为

D=(v′-v)sin σC

(19)

式中，v、v′分别为主、副平底的坐标值。

选取v为横坐标，r0、α为纵坐标，绘制r0-v和α-v曲线，如图11所示。

(a)r0-v的曲线

据r0-v和α-v曲线可知r0、α、D等重要尺寸和性能参数与v(v′)之间的联系。综合本文和文献[5]，得到如下结论：

(1)取值域[vC1max, vρmax)内，r0、α皆单调递减。v=vρmax时，主凸轮机构的最优解r0=r0min，α=αmin=αopt。

(3)共轭凸轮机构。由σC∈(σCmin, σCmax)可知，在(σCmin, σCmax)内任取一个σC，皆有

D∈(Dmin, Dmax)

(20)

图12 Dmin- σC和Dmax- σC曲线

5 机构综合示例

据文献[5]式(1)，算得s20=106.6554 mm，s2m=170.5675 mm。

σ=60°时，据文献[5]理论和算例，主凸轮机构解不存在。

σ=85°时，主凸轮机构的机构解存在，结果详见文献[5]中算例。

主凸轮机构中，l=108.0799 mm，L∈[113.0799，115.0799]mm[5]。副凸轮机构中，据本文理论，算得l′=106.3571 mm，L′∈[111.3571, 113.3571]mm。

6 结论

(2)通过对照比较，提出主凸轮机构、副凸轮机构彼此间的差异性内涵。

参考文献：

[1] 常勇, 杨富富. 作平面运动滚子从动件盘形凸轮机构的第Ⅱ类机构综合问题[J]. 机械工程学报, 2010, 46(21): 37-41. Chang Yong，Yang Fufu. Second Mechanism Synthesis Task of Disc Cam Mechanisms with Roller Follower Moving in Planar General Motion[J]. Journal of Mechanical Engineering, 2010, 46(21):35-41.

[2] 常勇, 杨富富. 作平面运动滚子从动件形锁合凸轮机构的第Ⅱ类机构综合问题[J]. 机械工程学报, 2012, 48(1): 39-46. Chang Yong，Yang Fufu. Second Mechanisms Synthesis Task of Positive-drive Disc Cam Mechanisms with Roller Follower Moving in General Planar Motion[J]. Journal of Mechanical Engineering, 2012, 48(1): 39-46.

[3] 常勇, 杨富富, 胡志超, 等. 作平面运动滚子从动件盘形凸轮机构的广义第Ⅱ类机构综合问题[J]. 机械工程学报, 2012, 48(15): 47-57. Chang Yong，Yang Fufu, Hu Zhicha, et al. Research on the General Second Mechanisms Synthesis Task of Disc Cam Mechanisms with Roller Follower Moving in General Planar Motion[J]. Journal of Mechanical Engineering, 2012, 48(15): 47-57.

[4] 车林仙. 支撑函数法在作平面复杂运动平底从动件盘形凸轮机构设计中的应用[J]. 机械设计, 2002, 19(4): 10-12. Che Linxian. The Application of Support Function Method in the Design of Disc Cam Mechanism Whose Flat-bottomed Follower Moves in the Form of Complicated Planar Motion[J]. Mechanical Design, 2002, 19(4): 47-57.

[5] 李延平, 林荣富, 常勇. 浮动平底推杆凸轮机构的第Ⅱ类尺寸综合问题[J]. 中国机械工程, 2015, 26(5):611-619. Li Yanping, Lin Rongfu, Chang Yong. Class Ⅱ Synthesis of Cam Mechanism with Floating Flat Faced Pushrod[J]. China Mechanical Engineering,2015, 26(5):611-619.

[6] 常勇, 林荣富, 李延平. 做平面运动滚子从动件盘形凸轮机构第Ⅱ类综合问题的广义化研究[J]. 中国机械工程, 2014, 25(5): 669-678. Chang Yong, Lin Rongfu, Li Yanping. General Class ⅡSynthesis of Disc Cam Mechanism with Roller Follower Moving in General Motion[J]. China Mechanical Engineering, 2014,25(5): 669-678.

[7] 常勇, 林荣富, 李延平. 浮动平底推杆—盘形凸轮组合机构的第Ⅰ类机构综合问题[J]. 中国机械工程, 2015, 26(12): 1584-1595. Chang Yong, Lin Rongfu, Li Yanping. General Class ⅠSynthesis of Disc Cam Mechanism with Roller Follower Moving in General Motion[J]. China Mechanical Engineering, 2015, 26(12): 1584-1595.

[8] 常勇, 林荣富, 李延平. 做平面运动滚子从动件盘形凸轮机构的深度广义第Ⅱ类综合问题[J]. 中国机械工程, 2014, 25(16): 2149-2158. Chang Yong, Lin Rongfu, Li Yanping. Deep General Class Ⅱ Synthesis of Disc Cam Mechanism with Roller Follower Moving in Planar General Motion [J].China Mechanical Engineering, 2014, 25(16): 2149-2158.

[9] 常勇, 徐继杨, 黎庆. 推导凸轮廓线外凸性判据和曲率半径的一种新方法[J]. 黑龙江商学院学报(自然科学版), 1996, 12(2): 43-50 Chang Y, Xu Jiyang, Li Qing. A New Method for Deriving the External-convexity Criterion and Convature Radius Formula[J]. Journal of Heilongjiang Commercial College, 1996, 12(2): 43-50.

[10] Schoenherr J. Synthesis of Planar Cam Mechanics with Lowest Dimensions[J]. Mechanism and Machine Theory, 1993, 28(3)：317-325.

[11] Navarro O, Wu C J, Angeles J. Size-minimization of Planar Cam Mechanisms[J]. Mechanism and Machine Theory, 2001, 36(3)：371-386.

[12] Dasgupta A, Ghosh A. On the Determination of Basic Dimensions of a Cam with a Translating Roller-Follower[J]. Journal of Mechanical Design, 2004, 126(1)：143-147.

[13] 常勇, 杨富富, 李延平. 糖果包装机中凸轮-连杆组合机构的尺寸综合研究[J]. 中国机械工程, 2012, 23(17): 2023-2030. Chang Yong, Yang Fufu, Li Yanping. Research on Size Synthesis of Cam-linkage Mechanism in a Candy Packaging Machine[J]. China Mechanical Engineering, 2012, 23(17): 2023-2030.

[14] 吕庸厚, 沈爱红. 组合机构设计与应用创新[M]. 北京: 机械工业出版社, 2008.

[15] 石永刚, 吴央芳. 凸轮机构设计与应用创新[M]. 北京: 机械工业出版社, 2007.

(编辑张洋)

Narrow/Generalized ClassⅡ Synthesis of Conjugate Cam Mechanism with Floating Flat Face Pushrod

Chang Yong Wu Qiuping Li Yanping

Jimei University, Xiamen, Fujian, 361021