2016 年中考数学命题趋势与复习对策
2016-12-23刘顿
文/刘顿
潮语流言
2016 年中考数学命题趋势与复习对策
文/刘顿
为了更好地把握中考数学命题新趋势,提高复习备考的针对性和复习效率,现根据2015年中考数学命题的特点,预测2016年中考命题的趋势,并提出以下对策,供你复习时参考.
一、依标据本,突出基础
各地中考数学命题的依据是新课标,以课本为本,加大了对基础知识和基本技能的考查力度,不少题目是“题在书外,根在书内”,可以从课本中找到原型,或是源于课本并适度拓展的引申题.这些题目背景新颖,运算量不大,只要掌握基本概念即可顺利解答.
例1(2015年常德卷)-2的倒数等于().
例2(2015年湘西卷)分解因式:x2-4=.

解:x2-4=x2-22=(x+2)(x-2).
例3(2015年永州卷)如图1,∠1=∠2,∠A=60°,则∠ADC=度.
解:∵∠1=∠2,∴AB∥CD,
又∵∠A=60°,∴∠ADC=180°-∠A=120°.
填120.
温馨小提示:以上3道题都是课本原题或类似于原题,分别考查倒数的概念、因式分解、平行线的判定与性质,只要概念清楚,性质明晰,即可得到正确答案.这是典型的送分题,我们不能失分.基本知识是复习的重中之重.在总复习中,一定要回归课本,重视基础知识和基本技能,千万不要把眼光放在高分题、压轴题上,否则将会得不偿失.
二、贴近生活,关注热点
应用数学知识解决实际问题是学习数学的目的之一,应用题是命题的重点.特别是以社会关注的问题为素材的应用题(含图像、图表应用题),与生活、自然、社会相关或跨学科的情境应用题越来越受到命题者青睐.
例4(2015年衡阳卷)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间的函数关系如图2所示(当4≤x≤10时,y与x成反比).
(1)根据图像分别求出血液中药物浓度上升阶段和下降阶段y与x之间的函数关系式;
(2)问血液中药物浓度不低于4微克/毫升的持续时间为多少小时?

解:(1)由图像可知,当0≤x≤4时,设y越kx.
当x越4时,y越8,∴4k越8,解得k越2.
∴y越2x(0≤x≤4).
当x越4时,y越8,∴m越4×8=32,
血液中药物浓度上升时y越2x(0≤x≤4);血液中药物浓度下降时y越(4≤x≤10).
(2)血液中药物浓度不低于4微克/毫升,即y≥4,
∴2≤x≤8,即持续时间为6小时.
温馨小提示:把生活中的实际问题作为命题的素材,考生感到亲切,有助于在解决问题过程中感受数学的应用价值,做到学以致用.在总复习时,要关注社会热点问题,如市场经济、人民生活、能源交通、生态环保等,学会用数学眼光观察社会,用数学思想分析问题,用数学方法解决问题,实现生活数学化,数学生活化,不断增强“学数学,用数学”的意识.
三、阅读理解,引领创新
数学学习是一个生动活泼、主动进取、灵活应用的过程,要改变过分依赖模仿与记忆的学习方式.近年来许多地方加大了在阅读理解和创新应用方面的考查力度,出现了不少令人耳目一新的试题.
例5(2015年郴州卷)阅读下面的材料:
如果函数y越(fx)满足:对于自变量x的取值范围内的任意x1,x2,若x1<x2,都有(fx1)<f(x2),则称(fx)是增函数;若x1<x2,都有f(x1)>f(x2),则称(fx)是减函数.
证明:假设x1<x2,且x1>0,x2>0,(fx1)-(fx2)越,
由假设得x2原x1>0,且x1x2>0,
根据以上材料,解答下面的问题:
(2)请仿照材料中的例题证明你的猜想.
(2)证明:假设x1<x2,且x1>0,x2>0,

由假设得x2+x1>0,x2-x1>0,且x1x2>0,

∴函数f(x)=1(x>0)是减函数. x2
温馨小提示:认真阅读题目中介绍的新知识,包括定义、公式、表示方法及如何计算等,并且正确理解新知识,读懂范例的应用,仿照范例解题,防止出错.解决这类问题,对阅读能力、观察能力、建模能力、创新能力的要求都比较高.
四、重视开放,强化探索
开放探索型试题有一定的自主性,给不同考生展示自己才华的舞台.它是必考的题型,几乎每份试卷都涉及.
例6(2015年张家界卷)如图3,AC与BD相交于点O,且AB=CD,请添加一个条件,使得△ABO≌ΔCDO.

分析:由对顶角相等得∠AOB=∠COD,要使△ABO≌ΔCDO,只需∠A=∠C或∠月=∠阅或粤月∥悦阅.
例7(2014年株洲卷)已知关于x的一元二次方程(a+c)x2+2bx+a-c=0,其中a、b、c分别为△ABC三边的长.
①如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
②如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
③如果△ABC是等边三角形,试求这个一元二次方程的根.
分析:这是一组结论探索型问题,都是根据已知条件,探索相关的结论.
①直接将x=-1代入方程,得到关于a,b的等式,可知a越b,即ΔABC是等腰三角形.
②利用方程有两个相等的实数根,得到(2b)2-4(a+c)(a-c)=0,∴a2=b2+c2,
∴△ABC是直角三角形.
③当△ABC是等边三角形时,a=b=c,方程可整理为x2+x=0,解得x1=0,x2=-1.
温馨小提示:开放探究型试题的知识覆盖面较广,综合性较强,对解题方法的要求较高.解答这类试题时,要注意各知识点之间的联系,选择合适的解题途径作答.
五、把握重点,凸显思想
重点知识是支撑学科体系的主要内容,一直保持较高的考查比例,并达到一定的考查深度,构成了数学试卷的主体.数学方法是数学知识在更高层次上的抽象和概括,它蕴含在数学知识的形成、发展和应用过程中,是促进考生数学素养和能力提高的基础,在考查重点知识的过程中,都重视考查数学方法.
例8(2015年长沙卷)长沙红星大市场某种高端品牌的家用电器,若按标价打八折销售该电器一件,则可获纯利润500元,其利润率为20%.现如果按同一标价打九折销售该电器一件,那么获得的纯利润为().
A.562.5元B.875元C.550元D.750元
解:设进价为x元,根据题意,得20%·x越500,解得x越2500,
∴标价为(2500+500)÷0.8=3750(元),纯利润为3750×0.9-2500越875(元).选B.

温馨小提示:在中考试题中,对数学思想的考查往往蕴含在对具体问题的分析过程中,是隐而不露的,需要考生去联想、去运用.在解决某一个数学问题时,常常要用到多种数学思想.在总复习中一定要重视对常用数学思想的总结与提炼,要通过对典型问题的分析、思考、总结,弄清什么样的问题用什么样的方法来解决,并内化为经验,自觉地加以应用.
六、学科整合,重视衔接
各学科知识的整合是培养良好思维品质和创新精神的有效途径.数学作为基础学科,在各学科中有着广泛的应用.一些跨学科的数学问题,要求在较大知识背景中利用数学知识分析问题并解决问题,有利于我们展示自己的综合素质,提高综合运用知识解决问题的能力.
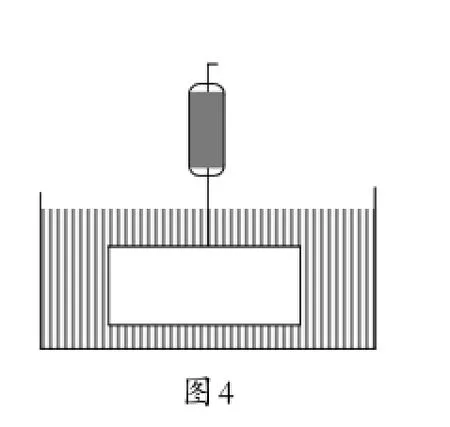
例10(2015年娄底卷)如图4,挂在弹簧秤上的长方体铁块浸没在水中,提着弹簧秤匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧秤的读数F(kg)与时间t(s)的函数图像大致是().

分析:开始一段时间,铁块在水中的重量保持不变,当铁块进入空气的过程中,重量逐渐增大,直到全部进入空气,重量保持不变.因此,弹簧秤的读数:保持不变→逐渐增大→保持不变.选A.
温馨小提示:重视学科之间知识的综合运用,要善于运用数学知识解决其他学科的问题,也要善于运用其他学科知识解决数学问题,进而提升自己的思维品质,培养自己的创新精神.
责任编辑:王二喜
