善用衍生结论,巧解关于三角形外心的向量问题

江苏省南通市通州区二甲中学(226321)陆忠华

善用衍生结论,巧解关于三角形外心的向量问题

江苏省南通市通州区二甲中学(226321)陆忠华

在近年的数学模拟考试、期末考试中,出现了一类关于三角形外心的向量问题,考生普遍反应题目难,解题方向不明确,存在较大的解题障碍.笔者研究后发现,该类问题如果能善用一个解题的衍生结论,那么解题的方向会豁然开朗,“难题”将不再是“难题”.

下面我们先来探究一个问题:

已知如图1,△ABC的三边分别为a,b,c,点O是△ABC的外心,试用边长a,b,c表示下式:

图1

图2

图3

利用此衍生结论,可以很好地解决与三角形外心有关的问题,下面我们举例来说明.

一、利用衍生结论解决求值问题

图4

二、利用衍生结论解决求范围问题

例3(2012年无锡高三期末第13题)设点O是△ABC的三边中垂线的交点,且AC2−2AC+AB2=0,则的取值范围是___.

分析:已知条件是关于边的二次关系,利用衍生结论(3)可以将目标转化成边的关系,在结合二次函数知识可以解决.

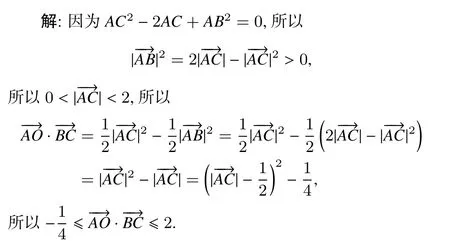
三、利用衍生结论解决多参量问题

通过以上各例,我们会发现,类似问题之所以能被简单的解决,关键在于衍生结论的使用,提供了问题处理的方向,找到了问题转化的途径.对衍生结论的研究,使我们对关于三角形外心的向量表示式有了进一步的认识,更能厘清向量与数量之间的转化关系,提高了学生的解题能力,加深了学生对数学的认知.