电压暂降随机预估的非序贯蒙特卡罗方法研究
2016-12-23郝晓弘
陈 伟,王 玲,王 丹,郝晓弘
(1.兰州理工大学电气工程与信息工程学院,兰州 730050;2.中国船舶重工公司第705所,西安 710075)
电压暂降随机预估的非序贯蒙特卡罗方法研究
陈 伟1,王 玲1,王 丹2,郝晓弘1
(1.兰州理工大学电气工程与信息工程学院,兰州 730050;2.中国船舶重工公司第705所,西安 710075)
针对电压暂降随机预估中蒙特卡罗法计算效率低、耗时长的缺陷,提出基于非序贯蒙特卡罗法对电压暂降进行随机预估。研究建立了电压暂降故障状态变量的数学模型,并利用Matlab/Simulink建立了IEEE-9节点测试系统模型,得到了故障模型的状态变量。通过分析电压暂降幅值的概率分布,并用非序贯蒙特卡罗法和蒙特卡罗法分别对电压暂降指标进行仿真计算。IEEE-9节点算例表明,该算法较蒙特卡罗法可快速收敛,提高了计算速度,具有良好的稳定性。
电压暂降;随机预估;非序贯蒙特卡罗法;故障状态变量
电压暂降也称为电压骤降[1-2],是指在某一时刻电压幅值突然偏离正常工作范围,经很短的一段时间后又恢复到正常状态的现象。IEEE标准中电压暂降定义[3-4]为供电系统中某点的工频电压有效值突然下降至额定值的10%~90%,并在随后10 ms~1 min的短暂持续期后恢复正常。随着科学技术的发展和工业规模的扩大,各种敏感设备在工业上得到了广泛的使用,电压暂降可能造成敏感设备跳闸或者整个生产线的重新启动,从而造成巨大的经济损失[5]甚至意外的伤亡。其中,输配电系统的短路故障引起的电压暂降最为频繁,因此对故障引发的电压暂降进行评估具有重要意义[6]。
电压暂降评估的方法主要有实测统计法和随机预估法[7-8]。实测统计法在较短的研究时间段内得到的结果可信程度不高,而长期的监测数据目前又难以得到。随机预估法主要有故障点法、临界距离法、解析法和蒙特卡罗模拟法等。故障点法[9]便于编制程序,文献[10]采用故障点法计算了电压暂降指标,研究了故障信息对电压暂降指标的影响。但使用该法时必须对系统故障进行大量的仿真以得到精确的结果,该法并不胜任大规模系统的电压暂降快速评估。临界距离法[11]计算模型简单,Bollen在文献[12]中以一个典型的辐射状配电系统为例,利用临界距离法详细地阐述了电压暂降的幅值和频度的计算方法,但该法只适合计算辐射性网络的暂降情况,且不具有随机性。解析法[13]具有精度高、理论成熟的特点,但该方法只考虑单点故障,未考虑系统发生多重故障的情形,且忽略了故障电阻的影响。蒙特卡罗法[14]在电力系统的可靠性分析中已得到成功应用,文献[15]利用马尔可夫链蒙特卡罗法MCMC(Markov chain Monte Carlo)得到各种故障信息,统计分析得出各节点电压暂降的各项评估指标,但该方法具有明显的统计性质、耗时长、占用内存大、计算效率低的缺点。
针对传统蒙特卡罗法的不足,本文采用非序贯蒙特卡罗法,通过建立故障状态变量的概率分布模型,产生故障变量的随机抽样值,测量并记录负荷处的电压特征量,然后对仿真结果进行统计分析,从而得到负荷处的电压暂降特征。
1 非序贯蒙特卡罗法的基本原理
非序贯蒙特卡罗法通常被称为状态抽样法,被广泛用在电力系统可靠性评估中。该方法的依据是系统状态是所有元件状态的组合,且每个元件状态可由对元件出现在该状态的概率进行抽样来确定。
每个元件可用在[0,1]区间的均匀分布来模拟。假设系统由N个元件组成,每个元件有失效和工作两个状态,且元件失效是相互独立的。令si代表元件i的状态,Qi代表其失效概率,则对元件i产生在[0,1]区间均匀分布的随机数Ri,即
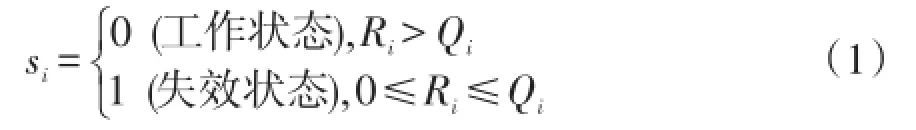
抽取N个随机数R1,…,Ri,…,RN,运用式(1)能确定系统状态s=(s1,…,si,…,sN),重复上述过程NS次,则能得到一个包含NS个系统状态样本的集合
系统状态在抽样中被选定后,则进行系统分析以判断其是否是故障状态,如果是,则对该状态的可靠性指标函数进行估计。
非序贯蒙特卡罗法使用的可靠性指标统一计算公式为
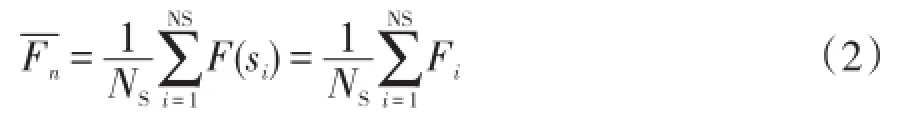
式中:F(s)是以系统状态s作为自变量的可靠性指标测试函数;Fn是随机函数F(s)的样本均值,当F(s)取不同测试函数时,Fn也就代表不同的可靠性指标。
由大数定律可知,相互独立、相同分布、具有有限数学期望的随机变量序列,对任何ε>0,有
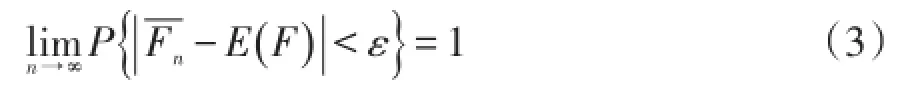
由此可见,在非序贯蒙特卡罗法中,随机函数F(s)子样的算术平均值,当n→∞时,以概率1收敛于数学期望E(F)。但在实际应用中,抽样的点数n不可能太大,否则计算成本太高。因此,应根据实际允许误差,合理选择n的数值,以实现计算精度和效率的综合权衡。
当抽样的数量足够大时,系统状态s的抽样频率可作为其概率的无偏估计,即

式中:M是抽样数;m(s)是在抽样中系统状态s出现的次数。
在运用非序贯蒙特卡罗法计算和评估电压暂降概率时一般分为3步[16]:①构造故障的概率模型;②实现从已知概率分布的抽样;③统计量的评估。
2 故障状态变量数学模型的建立
构造故障的概率模型中,故障信息包括故障线路、故障类型以及故障位置,这些故障状态变量通过非序贯蒙特卡罗法随机产生。
2.1 故障线路
X表示故障线路的状态变量,由m个单变量组成,m为进行状态抽样的线路条数。

式中Xi表示第i条线路的随机状态变量。在该方法概率仿真计算中,随机状态变量由随机数向量确定。通过伪随机数发生器产生m个在[0,1]上均匀分布的随机数xi,构成m维随机数向量x。

Xi与xi的关系为

式中Pi是线路i的故障率,i=1,…,m。
2.2 故障类型
将区间[0,1]按故障类型数分为k个区间,各区间长度mi满足如下关系式:
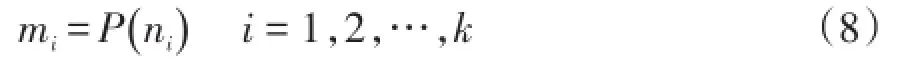
算法中k取值为4,即考虑4种类型的故障,并进一步细化为如下10种情况[17]:①A相接地短路;②B相接地短路;③C相接地短路;④AB两相短路接地;⑤AC两相短路接地;⑥BC两相短路接地;⑦三相短路;⑧AB相间短路;⑨AC相间短路;⑩BC相间短路。
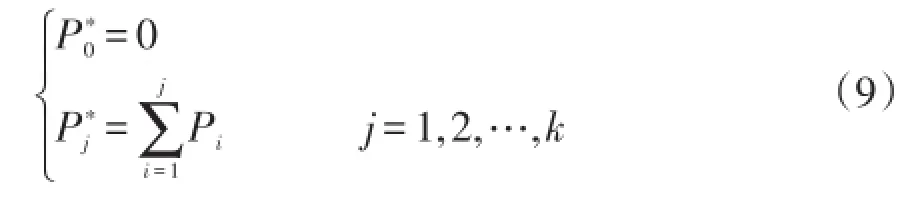
2.3 故障位置
故障位置用故障点到线路首端距离的标么值λij表示。对于故障线路Lij,若K为故障点位置,如图1所示,则LiK=λijLij。
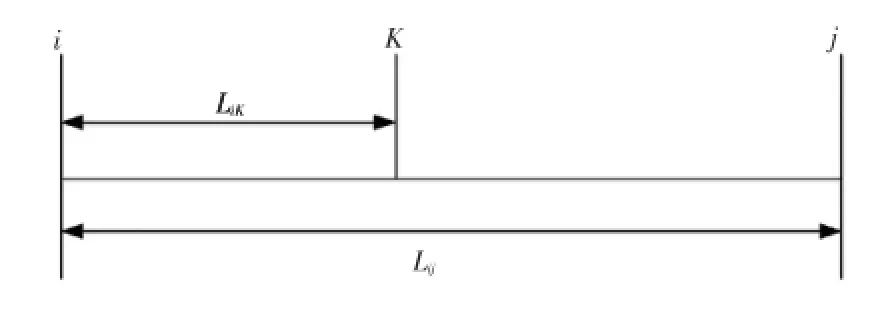
图1 线路故障位置的确定Fig.1 Fault location of line
3 电压暂降的评估指标
期望值描述了随机变量输出值的平均大小,电压暂降幅值的期望值更能体现多次抽样运算中各节点电压暂降的特性。本文采用节点处故障发生的频度作为电压暂降的评估指标,计算公式如下:
(1)电压暂降节点处故障发生的频度为

(2)电压暂降幅值的期望值公式为

式中:FTi为节点i发生故障的次数;Uig为节点i第g次电压暂降的幅值;N为电压暂降的总次数。
4 算例分析
为验证本文所提方法的有效性,在IEEE-9节点测试系统[18]上进行仿真研究,以Matlab/Simulink为仿真软件。
4.1 IEEE-9节点测试系统
IEEE-9节点测试系统接线如图2所示。该系统由3台发电机、9条母线和6条线路组成,仿真过程中做以下假设:
(1)系统运行方式不变;
(2)断路器为理想状态;
(3)每次故障时只有1条线路发生1种故障。
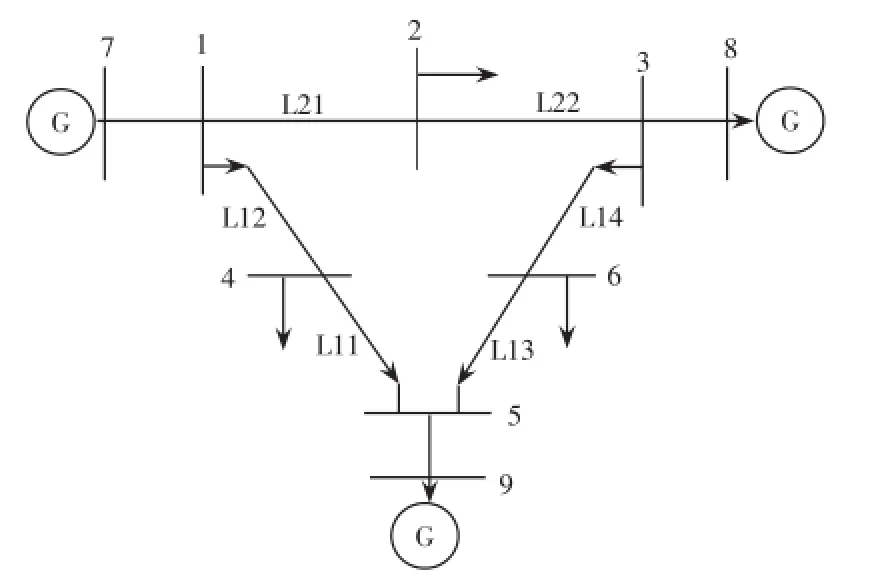
图2 IEEE-9节点系统接线Fig.2 Wiring diagram of IEEE 9-node power system
4.2 仿真结果和分析
采用伪随机数发生器进行大量抽样得到样本,从中随机抽取10 000次故障信息进行仿真计算,统计分析得到各节点电压暂降幅值的概率分布,如表1所示。
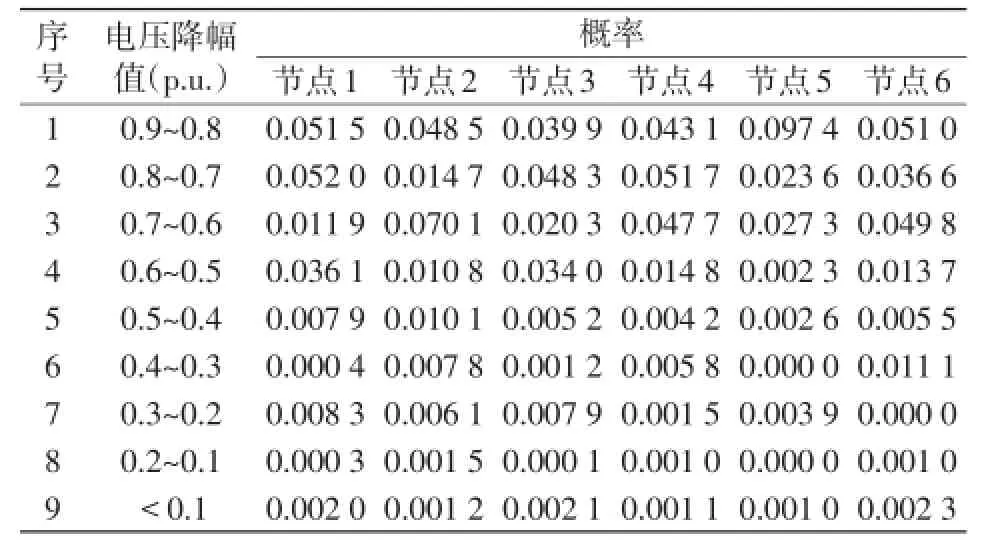
表1 各节点电压暂降幅值的概率分布Tab.1 Probability distribution of magnitudes of voltage sags at different nodes
从表1中可得出以下结论:
(1)低幅度(0.7~0.9 p.u.)的电压暂降概率要远大于大幅度(<0.7 p.u.)的电压暂降概率。各节点电压暂降的幅值绝大部分都分布在0.6 p.u.以上,与实测统计法[2,7]的结果非常接近,说明了本文方法的准确性。
(2)节点5发生电压暂降的概率比其他5个节点高很多,说明节点5更易受到电压暂降的影响。
利用蒙特卡罗法和非序贯蒙特卡罗法仿真得到的各节点电压暂降概率的指标的计算结果如表2所示。从中可以得出以下结论:
(1)非序贯蒙特卡罗法与蒙特卡罗法得到的指标参数值非常相近,说明了本文方法的有效性。
(2)节点1和节点3的故障频度大致相等,且高于其他4个节点的故障频度值,说明节点1和节点3更容易发生故障。
(3)节点5电压暂降幅值的期望值比其他节点高很多,说明随机故障对节点5电压暂降的幅值影响较小。
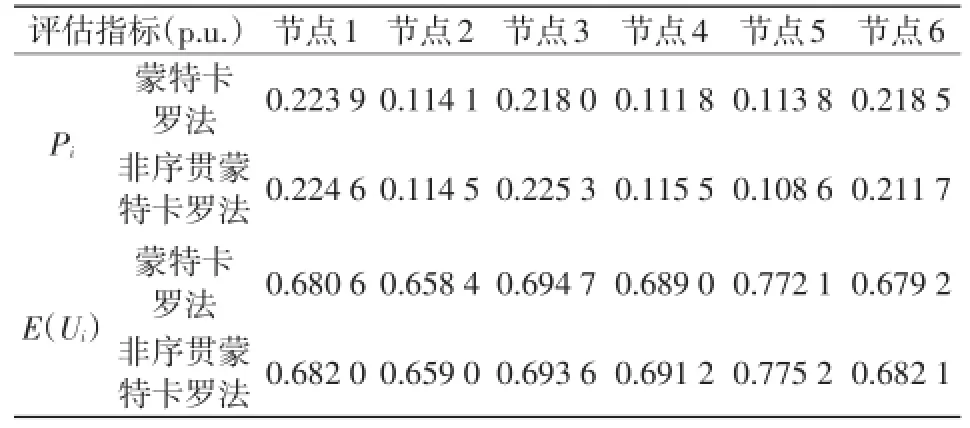
表2 各节点电压暂降的概率指标Tab.2 Probabilistic indices of voltage sags at different nodes
4.3 两种算法收敛速度的比较
以节点1为例,图3和图4分别为节点1的Pi和E(Ui)两个指标的收敛曲线。从图3和图4中可以看出,使用非序贯蒙特卡罗法采样约1 000次时电压暂降的指标参数就已经收敛。因此,非序贯蒙特卡罗法相对于蒙特卡罗法采样次数减少,计算速度加快。
4.4 两种算法稳定性的比较
为了检验两种算法的稳定性,以节点1为例,将蒙特卡罗法和非序贯蒙特卡罗法分别进行10次仿真计算。图5和图6分别为节点1使用这两种方法计算10次的故障率。比较可知,非序贯蒙特卡罗法计算10次得到的结果基本一致,说明了该法的稳定性比蒙特卡罗法好。
从图6可以看出,每条曲线在采样10 000次之后,其故障率都可收敛到稳定值。但蒙特卡罗法每次采样所得到的结果相差较大,结果不稳定,要想得到稳定的计算结果就必须增加采样次数。
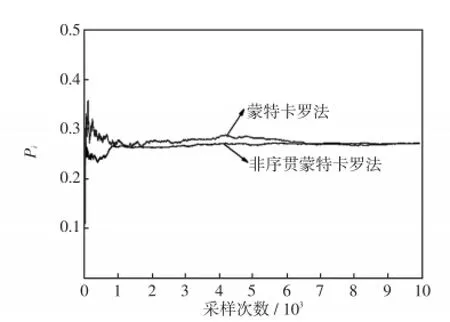
图3 两种方法节点1处Pi的收敛曲线Fig.3 Convergence curves for Piat node 1 using two methods
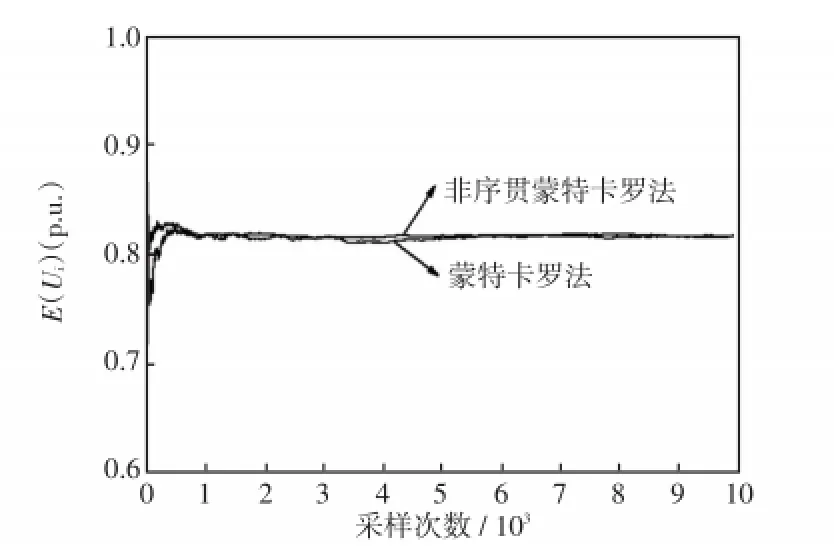
图4 两种方法节点1处E(Ui)的收敛曲线Fig.4 Convergence curves for E(Ui)at node 1 using two methods
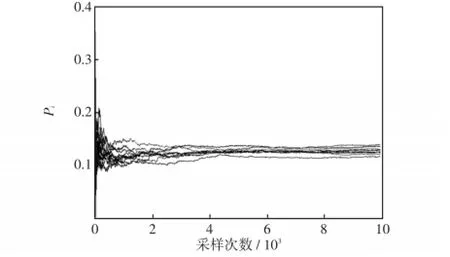
图5 蒙特卡罗法计算10次节点1的故障率Fig.5 Calculation of failure rate at node 1 using Monte Carlo method for ten times
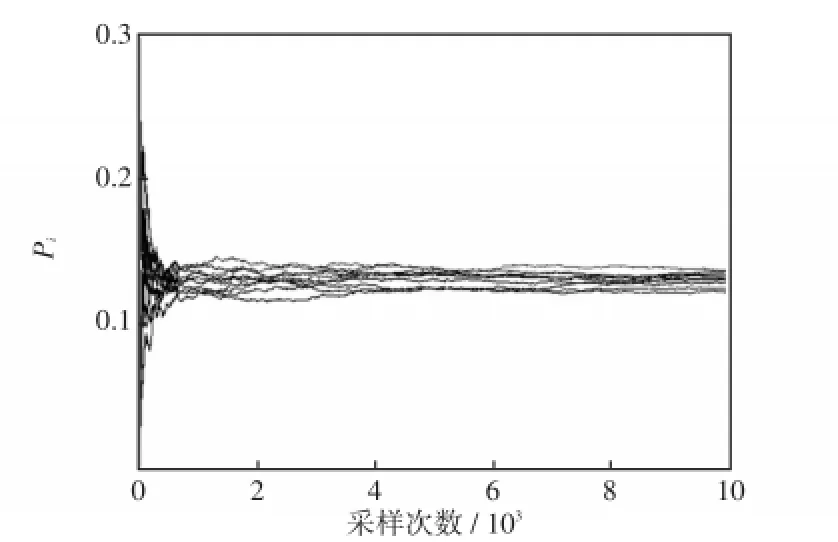
图6 非序贯蒙特卡罗法计算10次节点1的故障率Fig.6 Calculation of failure rate at node 1 using nonsequential Monte Carlo method for ten times
5 结论
本文在传统蒙特卡罗法的基础上,将非序贯蒙特卡罗法应用到了电力系统电压暂降的随机预估方法的研究中,得到以下研究结论:
(1)运行多次非序贯蒙特卡罗法所得到的结果十分稳定,而蒙特卡罗法的计算结果相差较大,必须以增加抽样次数的代价来得到稳定的指标。因此,非序贯蒙特卡罗法比蒙特卡罗法的稳定性更好。
(2)应用非序贯蒙特卡罗法时,只需进行较少次数的采样就可以获得较精确的计算结果,减少了采样时间,加快了计算速度。与蒙特卡罗法相比,非序贯蒙特卡罗法收敛速度快,节省了计算时间,计算速度得到了显著提高。
(3)将非序贯蒙特卡罗法应用于IEEE-9节点系统的电压暂降随机预估中进行电压暂降指标的计算,验证了本文所提方法的有效性和正确性。
[1]肖湘宁,徐永海(Xiao Xiangning,Xu Yonghai).电能质量问题剖析(Power quality analysis and its development)[J].电网技术(Power System Technology),2001,25(3):66-69.
[2]Lamoree J,Mueller D,Vinett P,et al.Voltage sag analysis case studies[J].IEEE Trans on Industry Applications,1994,30(4):1083-1089.
[3]肖湘宁.电能质量分析与控制[M].北京:中国电力出版社,2004.
[4]汪洋,徐方维,陈礼频,等(Wang Yang,Xu Fangwei,Chen Lipin,et al).基于改进S变换的电压暂降起止时刻检测(Voltage sag starting-ending moment detection based on improved S-transform)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2014,26(7):28-33.
[5]徐培栋,肖先勇,汪颖(Xu Peidong,Xiao Xianyong,Wang Ying).电压暂降频次两点估计随机评估方法(Voltage sags frequency stochastic assessment based on two-point estimate method)[J].电力系统保护与控制(Power System Protection and Control),2011,39(9):1-6.
[6]张鹏,郭永基(Zhang Peng,Guo Yongji).电压骤降的可靠性评估新方法(Probabilistic assessment of voltage sags in power systems)[J].电力系统自动化(Automation of Electric Power Systems),2002,26(8):20-24.
[7]Bollen M H J.Understanding Power Quality Problems Voltage Sags and Interruptions[M].New York:IEEE Press,2000.
[8]丁泽俊,刘平,欧阳森,等(Ding Zejun,Liu Ping,Ouyang Sen,et al).电能质量预测与预警机制及其应用(Mechanism of power quality forecast and early warning and their application)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2015,27(10):87-92.
[9]Becker C,Braun W Jr,Carrick K,et al.Proposed chapter 9 for predicting voltage sags(dips)in revision to IEEE Std 493,the Gold Book[J].IEEE Trans on Industry Applications,1994,30(3):805-821.
[10]Leborgne R C,Olguin G,Bollen M H J.Sensitivity analysis of stochastic assessment of voltage dips[C]//International Conference on Power System Technology,Singapore,Singapore,2004:69-74.
[11]Bollen M H J.Method of critical distances for stochastic assessment of voltage sags[J].IEE Proceedings-Generation,Transmission and Distribution,1998,145(1):70-76.
[12]Bollen M H J.The influence of motor reacceleration on voltage sags[J].IEEE Trans on Industry Applications,1995,31(4):667-674.
[13]Juarez Elisa Espinosa,Hernandez Araceli.Analytical approach for stochastic assessment of balanced and unbalanced voltage sags in large systems[J].IEEE Trans on Power Delivery,2006,21(3):1493-1500.
[14]宋云亭,郭永基,张瑞华(Song Yunting,Guo Yongji,Zhang Ruihua).电压骤降和瞬时供电中断概率评估的蒙特卡罗仿真(Probabilistic assessment of voltage sags and momentary interruption based on Monte-Carlo simulation)[J].电力系统自动化(Automation of Electric Power Systems),2003,27(18):47-51.
[15]郝晓弘,张思齐,陈伟,等(Hao Xiaohong,Zhang Siqi,Chen Wei,et al).基于MCMC法进行电压跌落随机预估方法的研究(Research on stochastic estimation of voltage sag based on MCMC method)[J].电力系统保护与控制(Power System Protection and Control),2013,41(9):94-99.
[16]于永利,朱小冬,张柳.离散事件系统模拟[M].北京:北京航空航天大学出版社,2003.
[17]陈瑞(Chen Rui).电压暂降在配电网中的传播规律及仿真评估研究(Research on Propagation Regularity and Simulation Assessment of Voltage Sags in Distribution System)[D].北京:华北电力大学电气与电子工程学院(Beijing:School of Electrical and Electronic Engineering of North China Electric Power University),2007.
[18]Anderson P M.Power System Control and Stability[M].Iowa,USA:The Iowa State University Press,1977.
Research on Random Estimation of Voltage Sags Based on Nonsequential Monte Carlo Method
CHEN Wei1,WANG Ling1,WANG Dan2,HAO Xiaohong1
(1.College of Electric and Information Engineering,Lanzhou University of Technology,Lanzhou 730050,China;2.705 Research Institute,China Shipbuilding Industry Corporation,Xi'an 710075,China)
Since Monte Carlo method suffers from low computation efficiency and long time consumption in the random estimation of voltage sags,this paper presents a random estimation method based on nonsequential Monte Carlo method.A mathematical model of state variables in the fault of voltage sags is built,and an IEEE 9-node test system model is established in Matlab/Simulink,which obtains the state variables of the fault model.The probability distribution of the amplitude of voltage sags is analyzed,and the indices of voltage sags are simulated by nonsequential Monte Carlo and Monte Carlo methods respectively.The results of the IEEE 9-node test system show that compared with Monte Carlo method,the proposed method improves the convergence,computation speed and stability obviously.
voltage sag;random estimation;nonsequential Monte Carlo method;fault state variable
TM74
A
1003-8930(2016)12-0026-05
10.3969/j.issn.1003-8930.2016.12.005
陈 伟(1976—),男,博士,教授,研究方向为电能质量分析与控制技术、新能源发电技术。Email:chenlin@lut.cn
王 玲(1987—),女,硕士研究生,研究方向为电能质量分析与控制。Email:wang.ling-ling@163.com
王 丹(1989—),女,硕士研究生,研究方向为智能化电气技术。Email:wd_snow@163.com
2015-04-22;
2016-06-06
国家自然科学基金资助项目(51267012,51467009);甘肃省科技支撑工业计划资助项目(1504GKCA033)
