分布式电源选址与定容的渐进最优场景算法
2016-12-23吴雪颖白晓清李佩杰
吴雪颖,白晓清,李佩杰
(广西电力系统最优化与节能技术重点实验室(广西大学),南宁 530004)
分布式电源选址与定容的渐进最优场景算法
吴雪颖,白晓清,李佩杰
(广西电力系统最优化与节能技术重点实验室(广西大学),南宁 530004)
精确模拟分布式电源输出的随机性,对分析分布式电源选址和定容对配电网的影响具有重要意义。本文基于Wasserstein距离指标的最优场景法构建风-光-荷多场景模型。以改进的电压分布指标为目标,结合含多场景模型、功率平衡及运行约束条件,建立分布式电源选址和定容对配电网电压稳定裕度影响最小的优化模型。通过两个配电网算例分析,结果表明合理选择分布式电源接入点的容量有利于提高配电网电压稳定裕度,能有效降低系统网损。
配电网;分布式电源;最优场景;电压稳定裕度;多场景
在分布式电源DG(distributed generation)选址和定容研究中,接入点和接入容量对配电网电压稳定、电压质量及损耗等方面有着直接影响[1-6]。文献[7-8]把分布式电源的出力等效为一个恒定功率输出的PQ型电源接入配电网,建立含投资费用、网络损耗、电压偏差等方面的多目标模型来优化DG接入配电网问题。但DG恒定出力的处理方式忽略了DG本身所具有的随机特性,难以模拟不可控DG对配电网的影响。文献[9]考虑了DG的零额、欠额及满额出力3种情况,建立以网损最小为目标,并提出了将分支向量搜索的更新方法与群搜索优化算法相结合,优化得到DG的接入点和接入容量。该文献考虑了DG出力的3个极端场景,在这3种情况下,分别计算DG出力对配电网的影响,但计算结果仅提供其相应点的目标值。文献[10]根据风机的输出特性,将其出力均分成有限个状态数,以高于置信水平的网络损耗最小为目标,建立一个多状态的DG优化模型。文献虽然已考虑了DG的多状态出力,但将DG出力均等分得到的场景不能较准确地描述原分布的波动性。对于求解随机非线性问题,一般采用离散概率分布形式表示连续分布的随机变量,采用蒙特卡罗[11]、拉丁超立方[12]等抽样方法实现。然而通过大量抽样再经聚类得到少量场景数和对应场景概率,其场景不能精确模拟DG的随机出力。此外,场景的质量严重依赖场景抽样的数量,且计算量大、周期长。因此,精确模拟DG的随机出力特性,对分析DG对配电网的电压稳定裕度影响至关重要。文献[13-14]已证明基于Wasserstein距离指标的渐进最优场景法生成的场景与原分布较为贴近,波动趋势与原分布近似一致,场景质量优于柯尔莫戈夫和等距离等场景方法。因此,本文采用该方法生成风电、光伏多状态出力,以保证场景的质量。此外,上述文献对DG选址问题的分析通常直接选择测试系统的重负荷节点或者支路末端节点作为DG接入点,不对接入点的选择进行决策。多状态出力情况下,这种处理方式容易忽略DG接入点对静态电压稳定问题产生的影响。
本文基于Wasserstein距离指标的最优场景法生成风电及光伏功率输出的渐进最优场景,运用场景树模型,建立风-光-荷的多场景模型。以改进的电压分布指标为目标函数,考虑含多场景风-光-荷模型的功率潮流平衡方程、变电站容量、节点电压、节点渗透率及支路电流等约束,建立DG选址与定容对配电网电压稳定裕度影响的数学模型。最后,以改进的IEEE14、IEEE33配电网系统作为算例进行计算和验证。计算结果表明最优接入DG有利于提高配电网电压稳定裕度,能改善系统的电压分布,降低系统的网络损耗。
1 风-光-荷多场景模型
1.1 渐进最优场景方法
采用离散概率分布表示连续型随机变量,其主要目的是用有限的离散值近似模拟连续型变量的随机特性,进一步简化相关数学模型的计算。根据原分布模拟的离散值必须满足两点:①应具有足以代表原分布的随机特性;②应与原分布的距离差尽可能小。文献[13-14]已证明基于Wasserstein距离指标的渐进最优场景方法模拟的场景精度优于其他距离函数指标。Wasserstein距离函数作为概率测度空间中两个概率密度函数间的距离函数,用于判断两个函数之间的相似度。因此,原分布G与模拟的离散分布之间的距离差可作为衡量模拟离散值的精度和质量。假设原概率边缘分布函数x~G和离散概率边缘函数,其Wasserstein距离为根据场景模拟的思想,假设在离散点集合S的概率测度为分位点zs(s=1,…,S)的点质量。要获得渐进最优场景,则需要找到概率测度函数的最优分位点zs,相继获得zs分位点所对应的概率pz,使得最小。
根据文献[14]采用渐进的求解策略得到单维随机变量的最优分位点zs,求解方程如下:
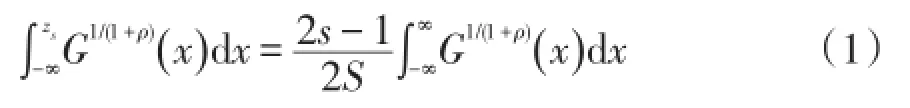
对应分位点zs的概率可根据式(2)~(4)计算得到

式中:z0为-∞;zS为+∞。
1.2 风电出力的渐进最优场景
本文用于生成风电功率场景的概率密度函数[14-16]为
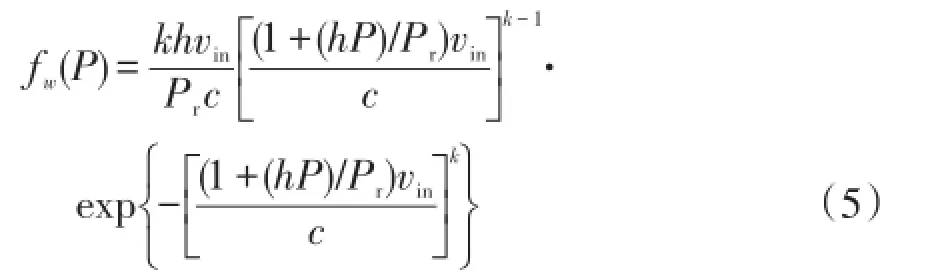
式中:P为风机输出功率;vin为风机的切入风速;;k、c分别是风机的形状系数和尺度参数,vr为风机的额定风速;Pr为风机的额定功率。
将概率密度函数代入最优场景分位点方程式(1)的右端项中,经化简得到式(6)为
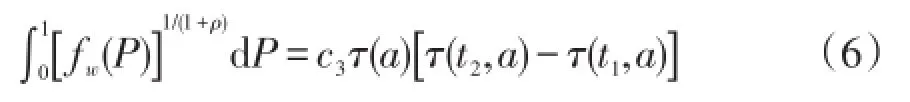
将概率密度函数代入最优场景分位点方程式(1)的左端项中,经化简得到式(7)为
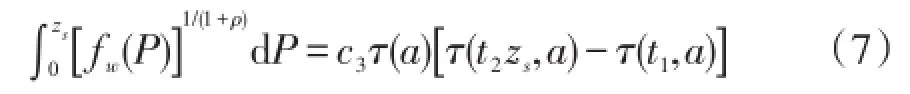
根据式(1)的左右项相等,相应得到的风电功率的最优场景分位点函数方程为
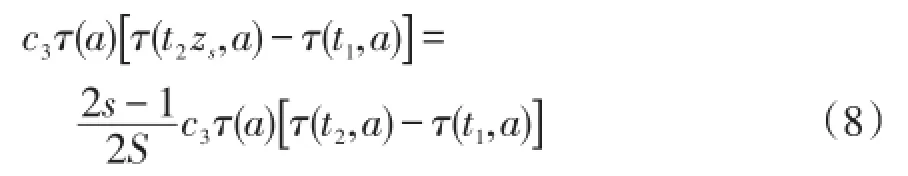
通过求解式(8),可以得到风电功率的最优场景分位点zs(s=1,…,S),再根据概率密度函数积分得到相应分位点的场景概率。
对于P=0和P=Pr两种情况的概率可以通过式(9)、(10)计算得到
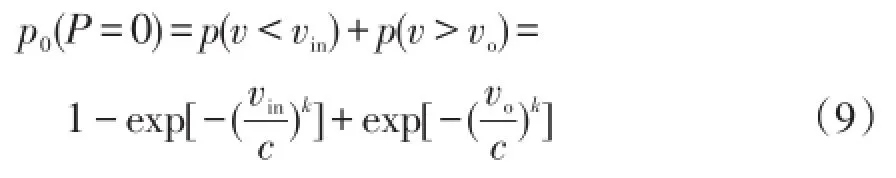
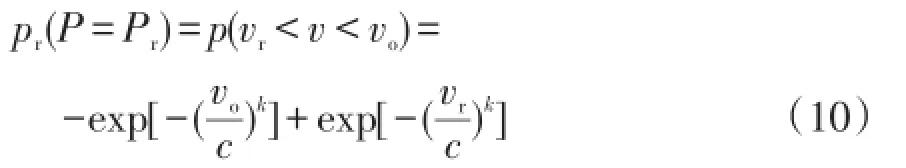
式中vo为风机的切出风速。
以此类推,对于光伏出力的渐进最优场景也能通过将Beta概率密度函数代入到最优场景的数学方程式(1)中,进行化简并求解,以生成光伏出力的渐进最优场景的分位点以及对应场景概率。
1.3 负荷模型
目前负荷预测精确度有限,因此未来任何时刻的负荷预测结果都应作为随机变量进行处理。本文采用类似风电模型处理方式,运用离散概率分布表示连续型随机变量分布,建立多状态负荷等效模型。根据文献[17]所提供的IEEE-RTS系统每小时负荷曲线,运用聚类技术[18]将负荷划分为nl个不同水平的负荷以及对应的概率pnl。
1.4 风-光-荷多场景模型
风-光-荷多场景模型包含了不同类型DG和负荷水平的所有排列组合。假设根据Wasserstein距离的渐进最优场景法生成风电出力的场景数为nw个,对应场景概率为pnw。光伏出力场景数为ns个,对应场景概率为pns;负荷的状态数为nl,对应场景概率为pnl,则总场景数N根据式(11)计算得到,风-光-荷的多场景空间集合为K(i,j,l),每个场景空间元素发生的概率根据式(12)对应每个随机变量的场景发生概率卷积得到
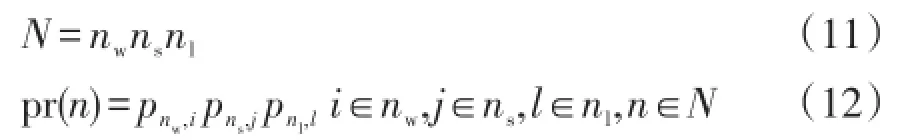
所以多场景风-光-荷模型空间集合可表示为
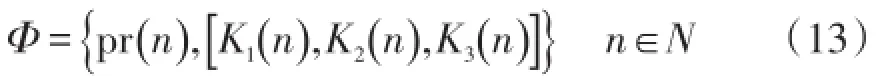
式中K1、K2、K3分别表示构成多场景空间集合K(i,j,l)的风电出力、光伏出力以及负荷的场景排列。
2 基于渐进最优场景的DG选址与定容模型
考虑DG的配电网规划目的是在满足系统用电需求的正常网络运行下,寻找最优的DG接入点以及接入容量,使得配电网的电压稳定裕度达到最大,进而改善配电网的电压分布。本文以DG接入后,配电网电压分布指标提高幅度最大为目标函数,建立含场景概率的目标函数[19,20]如下:

式中:pri为场景发生概率;μi为电压分布指标;m为系统节点数。
电压分布指标的表达式为

式中:Vp,withoutDG与Vp,withDG分别是DG接入前和接入后的电压分布;Vi为节点i电压;Li为节点i的负荷;m为系统节点数;Ki为各节点的权重因子。
假设满足以下约束条件:
(1)功率潮流等式约束为
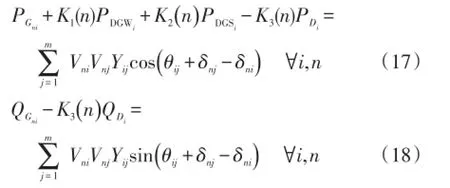
(2)节点电压约束为
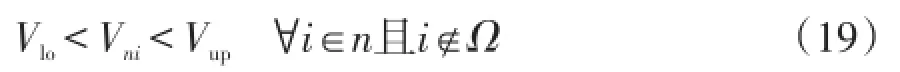
式中:Vlo为节点电压幅值下限值;Vup为节点电压幅值上限值;Ω为变电站母线集。
(3)支路电流约束为
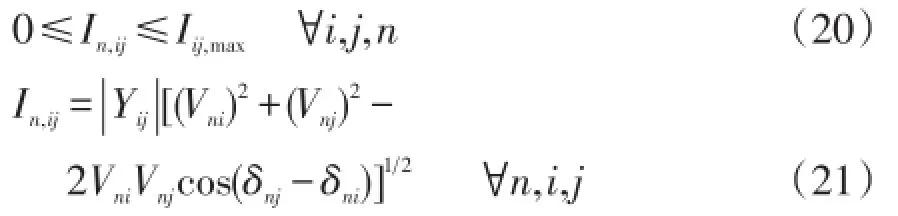
式中:Iij,max为节点i与节点j之间馈线电流容量限制;In,ij为第n场景节点i,j之间馈线电流。
(4)变电站容量约束为
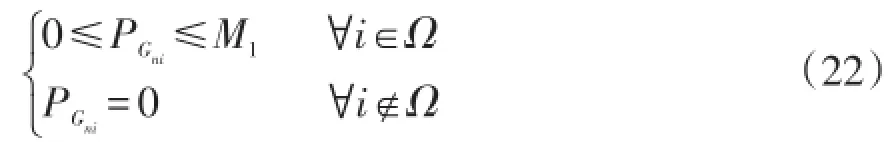
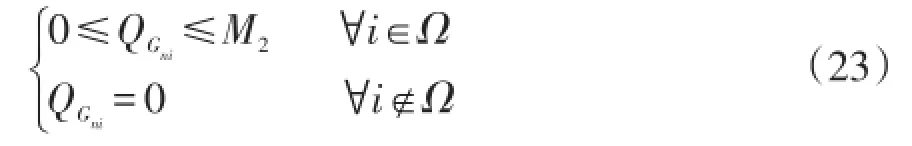
式中:M1为母线i的有功功率容量上限值;M2为母线i的无功功率容量上限值。
(5)节点渗透率约束为

式中:ai为整型变量;PRi为节点i的最大渗透容量限制;B为候选节点集。
(6)系统最大渗透率约束为
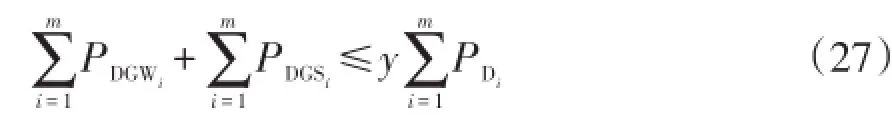
式中y为最大渗透率限制,即总峰值负荷的百分比。
本文所提模型求解流程见图1。
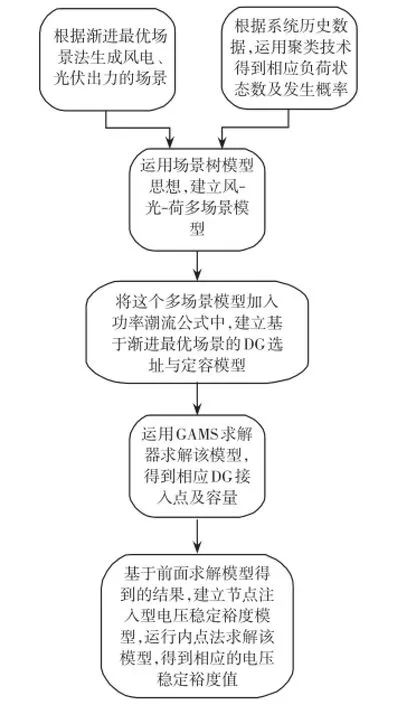
图1 模型求解步骤流程Fig.1 Flow chart of the solving process of the model
3 算例分析
本文采用改进IEEE14[21]、IEEE33[22]节点配电网测试系统作为算例,进行DG选址与定容的配电网规划。在算例中,风电出力最优场景数nw=6,光伏出力的最优场景数ns=6,负荷状态数nl=10,总的风-光-荷多场景空间状态数N=360。若只考虑单一DG,则风-光-荷多场景空间状态数N=60。在所建立的DG选址与定容的配电网规划模型中,涉及到DG模型的有关参数如表1、2所示。

表1 风机模型参数Tab.1 Parameters of wind turbine model

表2 光伏模块参数Tab.2 Parameters of PV module
3.1 场景模拟对比
运用场景及场景概率来表示连续型随机变量,所得到的场景分布应与随机变量的原分布波动性近似一致,且两分布间的距离差最小。以风电为例,根据图2场景模拟对比图,带星型虚线是加拿大某风电场一年的风功率历史数据统计[23]经聚类得到的功率输出百分比与场景概率的关系曲线;带圆点的虚线是根据风机功率输出特性,将其功率线性输出区间均分离散得到的功率输出百分比以及对应场景概率;实线是由渐进最优场景法得到的功率输出百分比和对应场景概率。由图2中曲线走势可知,渐进最优场景的曲线与历史数据曲线的波动趋势较贴近,能够准确模拟原分布的波动特点。因此,精确模拟DG的功率分布与准确预测场景发生概率对分析DG接入对配电网的影响具有重要意义。
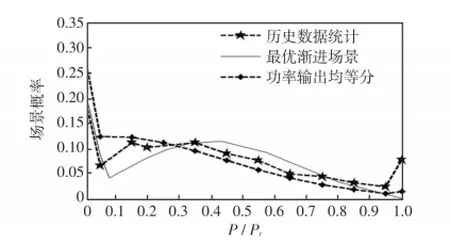
图2 场景模拟对比Fig.2 Comparison of senario simulation
3.2 DG接入情况分析及电压分布指标
基于渐进最优场景的DG选址与定容模型,运用GAMS的dicopt商业求解器[24]联立求解所建立的多场景数学模型。表3中的最优接入点和接入容量为模型求解的结果,电压分布指标为目标函数值。由电压分布指标定义可知,当电压分布指标大于1时,说明DG接入对配电网的电压分布有积极影响;当电压分布指标等于1或者小于1时,DG接入对配电网没有影响或者有消极影响。从表3中的电压分布指标可知,其值都是大于1,说明DG接入对配电网电压分布有积极影响。此外,根据表3中全网最低电压所示,DG接入后,全网的最低点电压有很大提高。由此可见,DG接入后对电压偏低情况有很大改善作用。
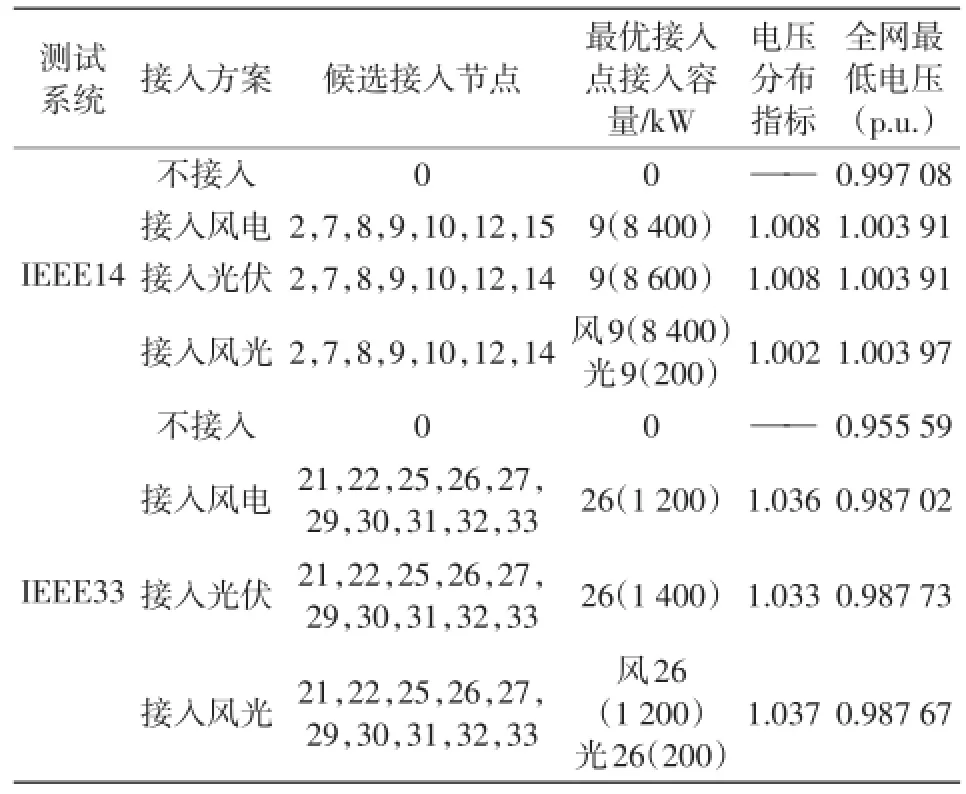
表3 测试系统的求解结果Tab.3 Solving results of test system
3.3 不同负荷增长方式的电压稳定裕度分析
表4为3种负荷增长方式所对应的测试节点集。3种负荷增长方式为增加重负荷节点的负荷(方式1),增加重负荷区域节点的负荷(方式2),增加所有节点的负荷(方式3)。采用3种不同负荷增长方式对DG接入前和接入后进行计算,对配电网电压稳定裕度的影响进行比较。根据模型求解得到的DG最优接入点和接入容量,运用基于现代内点理论的电压稳定临界点算法[25]求取不同负荷增长方式下的电压稳定裕度值。

表4 系统的测试节点Tab.4 Test nodes of the system
图3(a)、图3(b)分别为14节点和33节点配电网系统的测试结果,填充为圆点的柱形表示无DG接入的电压稳定裕度,填充为横斜杠的柱形表示DG接入的电压稳定裕度。由图3中柱形高度可以看出,对于任何一种负荷增长方式,接入DG的电压稳定裕度均高于不接入的情况。因此,DG接入后对配电网的电压稳定裕度有明显的提高作用。
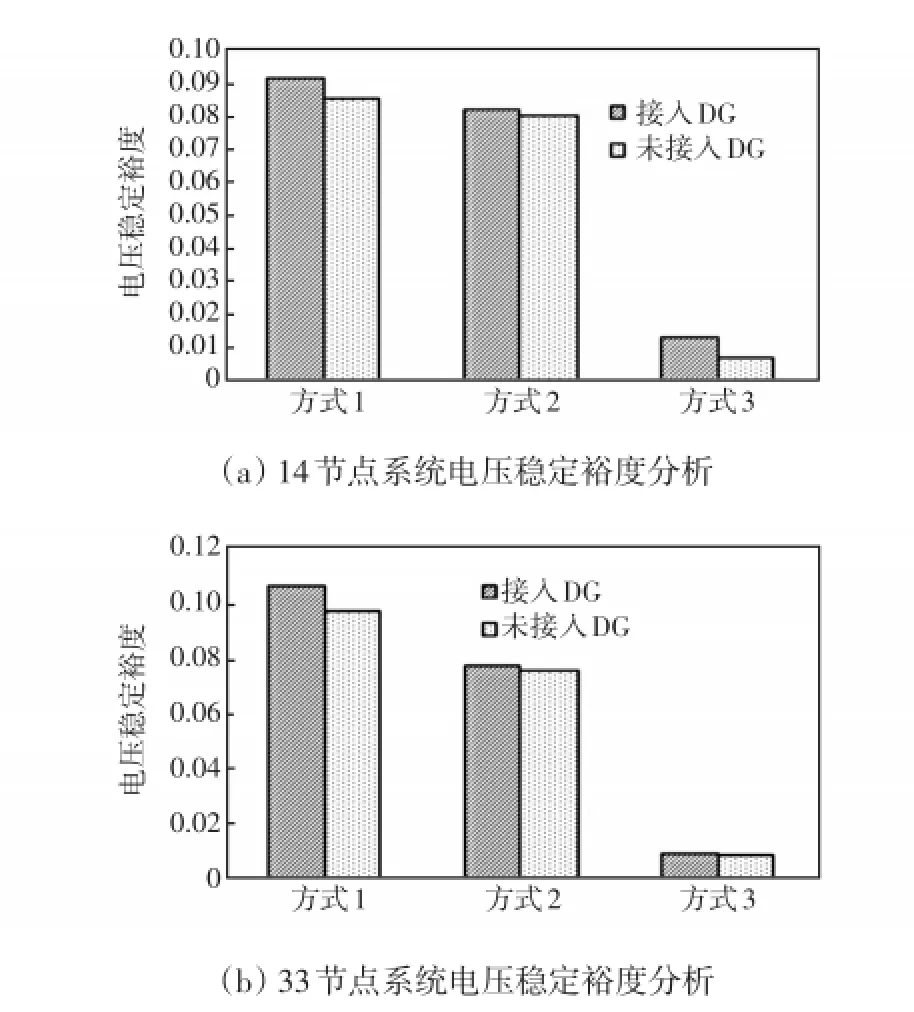
图3 电压稳定裕度分析Fig.3 Margin analysis of voltage stability
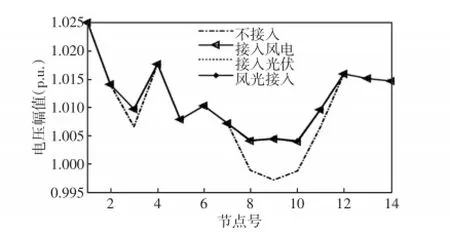
图4 14节点系统的电压分布情况Fig.4 Voltage distribution of 14-node system
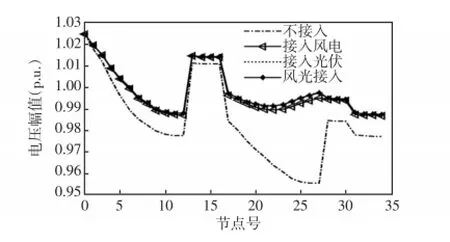
图5 33节点系统的电压分布情况Fig.5 Voltage distribution of 33-node system
3.4 分布式电源对电压的影响
图4、5是DG接入后对不同系统的电压影响。黑色点划曲线的特点是电压偏差较大,虽然多数节点电压幅值是满足系统要求,但是某些节点电压幅值低至0.96 p.u.以下,如33节点系统中节点24~27。对于负荷侧用户,电压偏低且质量较差,不仅对用电设备影响很大,而且会加大线路损耗。而由其他3条接入DG的曲线可知,DG接入后,原配电网电压偏低的节点得到了很大改善,明显改善了负荷侧电压质量。
3.5 损耗分析
长距离输电且末端轻载的配电网供电特点使得系统线路损耗成为不可避免的问题。为降低线路损耗,传统方法是安装无功补偿装置、节能变压器、多分裂导线、采用电阻率较小的导线等。线路损耗增大的主要原因是线路两端电压偏差增大。当DG分散式地接入配电网后,近距离向负荷供电,改变了原系统潮流分布,减少了节点间电压偏差,系统线路损耗也相应降低,且负荷侧电压质量也能大大提高。图6、7分别考虑风电、光伏单独接入对两个配电网系统的损耗影响。图6(a)、图7(a)为风电接入后的系统网损情况,图6(b)、7(b)为光伏接入后的系统网损情况。图6、7中,虚线是原系统无DG接入的网损情况,实线为DG接入系统后的网损情况。
若多场景模型为风-光-荷,则通过求解这个风-光-荷多场景DG选址与定容模型,得到所对应60个场景的网损值。由图6、7可知,DG接入后能有效改善两个系统的网损情况。此外,通过图6(a)、图7(a)与图6(b)、图7(b)对比可以看出,光伏输出功率比风电输出功率更加恒定,因此光伏接入对降低系统的网损效果较为显著。
图8是通过联立求解风-光-荷多场景DG选址与定容模型,得到的360个场景所对应的系统损耗。其中图8(a)为14节点系统网损,图7(b)为33节点系统网损。图8中虚线阶梯状是对应不同负荷水平下系统的网络损耗,实线为多场景风-光发电接入后对系统的网络损耗影响。根据场景树生成规律,每个负荷水平对应36个风-光组合数。由于风-光的不同状态功率交替输出,当DG总注入功率偏小时,对应的系统损耗也近似等于原系统损耗。同时,随着DG总注入功率逐渐增大,系统损耗随之大幅降低。
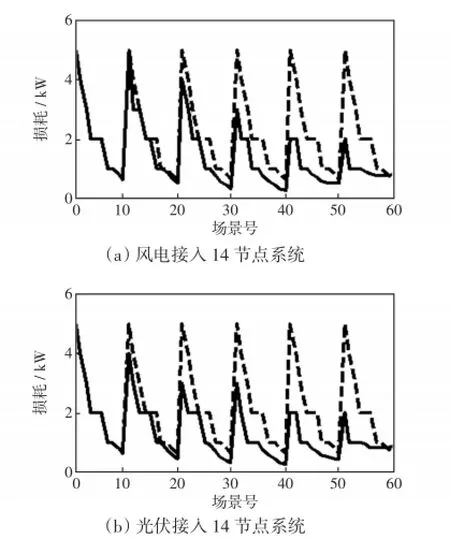
图6 不同类型分布式电源接入14节点系统对系统损耗影响Fig.6 Impact of different types of DG on system loss in 14-node system
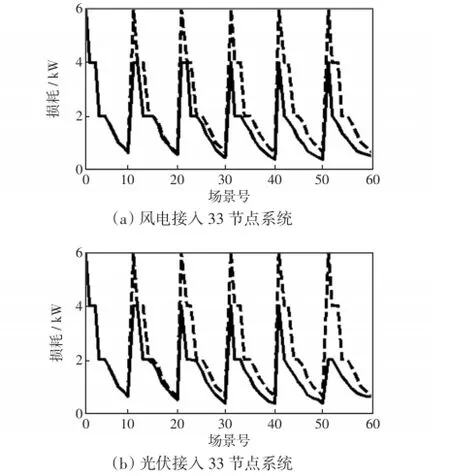
图7 不同类型分布式电源接入33节点系统对系统损耗影响Fig.7 Impact of different types of DG on system loss in 33-node system
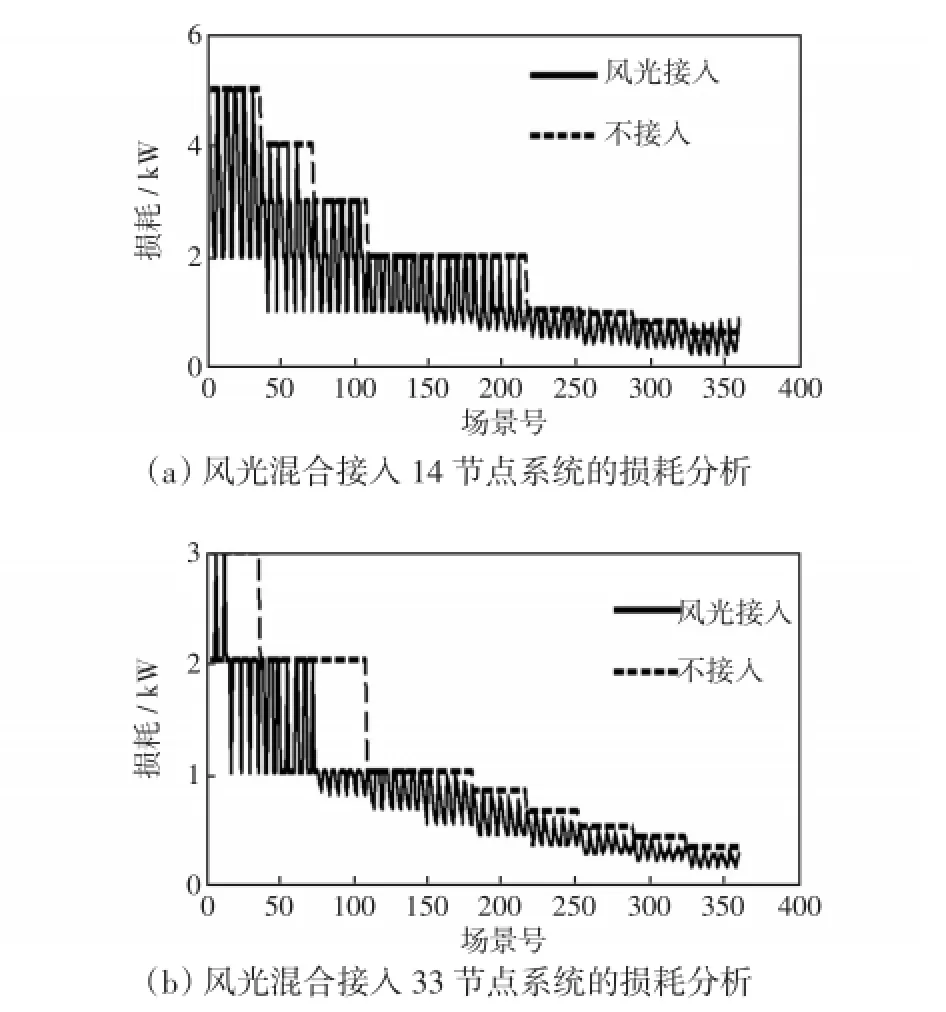
图8 风光混合接入对系统损耗的影响Fig.8 Impact of mixed generations of wind-photovoltaic on system losse
4 结论
本文考虑多类型DG和负荷的多场景情况,以改进的电压分布指标为目标函数,结合电网运行约束条件,建立了混合DG选址与定容对配电网电压稳定裕度影响的数学模型。通过对两个典型算例计算结果分析可知:
(1)最优接入DG有利于提高配电网电压稳定裕度,能改善系统的电压分布质量;
(2)风电和光伏混合接入比单一类型DG接入对降低系统网络损耗效果明显;
(3)基于Wasserstein距离指标的最优场景法可在生成较少场景数的同时,能保证精确模拟DG出力的随机特性,能降低求解相应数学模型的计算量。
[1]陈海焱,段献忠,陈金富(Chen Haiyan,Duan Xianzhong,Chen Jinfu).分布式发电对配网静态电压稳定性的影响(Impacts of distributed generation on steady state voltage stability of distribution system)[J].电网技术(Power System Technology),2006,30(19):27-30.
[2]李题印,韩永强,胡晓琴,等(Li Tiyin,Han Yongqiang,Hu Xiaoqin,et al).分布式发电接入电网的静态电压稳定特性及影响分析(Characteristics of static voltage stability for distributed generation integrated into power system and its impacts analysis)[J].电力系统保护与控制(Power System Protection and Control),2014,42(12):8-13.
[3]裴玮,盛鹍,孔力,等(Pei Wei,Sheng Kun,Kong Li,et al).分布式电源对配网供电电压质量的影响与改善(Impact and improvement of distributed generation on distribution network voltage quality)[J].中国电机工程学报(Proceedings of the CSEE),2008,28(13):152-157.
[4]彭建春,曾顺意,谢云岩,等(Peng Jianchun,Zeng Shunyi,Xie Yunyan,et al).考虑电压稳定的分布式发电最优配置(Optimal placement of distributed generation considering voltage stability)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2011,23(5):65-69.
[5]于建成,迟福建,徐科,等(Yu Jiancheng,Chi Fujian,Xu Ke,et al).分布式电源接入对电网的影响分析(Analysis of the impact of distributed generation on power grid)[J].电力系统及其自动化学报(Proceedings of the CSUEPSA),2012,24(1):138-141.
[6]卢锦玲,石少通,卢洋(Lu Jinling,Shi Shaotong,Lu Yang).含大规模风电场的电网静态电压稳定性评估(Static voltage stability assessment on the grid with largescale wind farm connection)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2015,27(6):73-80.
[7]栗然,马慧卓,祝晋尧,等(Li Ran,Ma Huizhuo,Zhu Jinyao,et al).分布式电源接入配电网多目标优化规划(Multi-objective optimization for DG integration into distribution system)[J].电力自动化设备(Electric Power Automation Equipment),2014,34(1):6-13.
[8]唐林权,李芝荣,李如琦,等(Tang Linquan,Li Zhirong,Li Ruqi,et al).基于最优引导策略的分布式电源优化配置(Distributed generation planning based on the optimized guidance strategy)[J].现代电力(Modern Electric Power),2014,31(1):23-27.
[9]周杨烯,黎灿兵,何禹清,等(Zhou Yangxi,Li Canbing,He Yuqing,et al).GSO算法在分布式电源选址与定容中的应用(Location and penetration of distributed generation based on group search optimizer)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2012,24(5):58-62.
[10]丛鹏伟,唐巍,张璐,等(Cong Pengwei,Tang Wei,Zhang Lu,et al).基于机会约束规划考虑DG与负荷多状态的配电网重构(Chance-constrained programming based distribution network reconfiguration considering multi-states of distributed generation and load)[J].电网技术(Power System Technology),2013,37(9):2573-2579.
[11]苏傲雪,范明天,李仲来,等(Su Aoxue,Fan Mingtian,Li Zhonglai,et al).计及风力发电影响的配电系统可靠性评估(Reliability evaluation of distribution system considering wind power effect)[J].电力系统保护与控制(Power System Protection and Control),2013,41(1):90-95.
[12]陈璨,吴文传,张伯明,等(Chen Can,Wu Wenchuan,Zhang Boming,et al).基于多场景技术的有源配电网可靠性评估(An active distribution system reliability evaluation method based on multiple scenarios technique)[J].中国电机工程学报(Proceedings of the CSEE),2012,32(34):67-73.
[13]Hochreiter R,Pflug G C.Financial scenario generation for stochastic multi-stage decision processes as facility location problems[J].Annals of Operations Research,2007,152:257-272.
[14]黎静华,韦化,莫东(Li Jinghua,Wei Hua,Mo Dong).含风电场最优潮流的Wait-and-See模型与最优渐近场景分析(Asymptotically optimal scenario analysis and waitand-see model for optimal power flow with wind power)[J].中国电机工程学报(Proceedings of the CSEE),2012,32(22):15-23.
[15]Liu Xian,Xu Wilsun.Economic load dispatch constrained by wind power availability:A here-and-now approach[J].IEEE Trans on Sustainable Energy,2010,1(1):2-9.
[16]Liu Xian.Economic load dispatch constrained by wind power availability:A wait-and-see approach[J].IEEE Trans on Smart Grid,2010,1(3):347-355.
[17]Grigg C,Wong P,Albrecht P,et al.The IEEE reliability test system-1996.A report prepared by the reliability test system task force of the application of probability methods subcommittee[J].IEEE Trans on Power Systems,1999,14(3):1010-1020.
[18]Singh C,Kim Y.An efficient technique for reliability analysis of power systems including time dependent sources[J].IEEE Trans on Power Systems,1988,3(3):1090-1096.
[19]Al Abri R S,El-Saadany E F,Atwa Y M.Optimal placement and sizing method to improve the voltage stability margin in a distribution system using distributed generation[J].IEEE Trans on Power Systems,2013,28(1):326-334.
[20]Chiradeja P,Ramakumar R.An approach to quantify the technical benefits of distributed generation[J].IEEE Trans on Energy Conversion,2004,19(4):764-773.
[21]万路路,王磊,丁昊(Wan Lulu,Wang Lei,Ding Hao).配电网电动汽车优化充电研究(Research on charging optimization for distributed plug-in hybrid EV)[J].华东电力(East China Electric Power),2011,39(12):2049-2053.
[22]Kirmani S,Jamil M,Rizwan M.Optimal placement of SPV based DG system for loss reduction in radial distribution network using heuristic search strategies[C]//International Conference on Energy,Automation and Signal,Bhubaneswar,India,2011.
[23]Atwa Y M,El-Saadany E F.Probabilistic approach for optimal allocation of wind-based distributed generation in distribution systems[J].IET Renewable Power Generation,2011,5(1):79-88.
[24]魏传江,等.GAMS用户指南[M].北京:中国水利水电出版社,2009.
[25]韦化,丁晓莺(Wei Hua,Ding Xiaoying).基于现代内点理论的电压稳定临界点算法(An algorithm for determining voltage stability critical point based on interior point theory)[J].中国电机工程学报(Proceedings of the CSEE),2002,22(3):27-31.
关于分类号、引言和结论
1 分类号
(1)为便于检索和编制索引,按《中国图书资料分类法》对每篇论文给出分类号。
(2)一篇涉及多学科的论文,可以给出几个分类号,主分类号应排在第1位。
2 引言(篇首)
(l)引言的内容可包括研究的目的、意义、主要方法、范围和背景等。应开门见山,言简意赅,不要与摘要雷同或成为摘要的注释,避免公式推导和一般性的方法介绍。
(2)引言的序号可以不编,“引言”二字可以省略。
3 结论(篇尾)
(1)结论是文章的主要结果、论点的提炼与概括,应准确、简明、完整、有条理。
(2)如果不能导出结论,也可以没有“结论”而进行必要的讨论。可以在结论或讨论中提出建议或待解决的问题。
摘编于《中国高等学校自然科学学报编排规范》(修订版)
Asymptotically Optimal Scenario Algorithm for the Locating and Sizing of Distributed Generation
WU Xueying,BAI Xiaoqing,LI Peijie
(Guangxi Key Laboratory of Power System Optimization and Energy Technology(Guangxi University),Nanning 530004,China)
To simulate the randomness of active power output from distributed generation exactly,it is important to analyze the impact of the locating and sizing of distributed generation on distribution network.A multi-scenario model of wind-photovoltaic-load is built based on the Wasserstein distance indicators to construct the optimal scenario.With the improved voltage distribution index as an objective function,optimization models are established to minimize the impact of the locating and sizing of distributed generation on distribation network,considering the multi-scenario model,power equilibrium and other operation constraints.The simulation results of two distribution systems show that a reasonable choice of the locating and sizing of distributed generation can help to improve the voltage stability margin of distribution system and reduce the system loss.
distribution system;distributed generation;optimal scenario;voltage stability margin;multiple scenarios
TM715
A
1003-8930(2016)12-0018-08
10.3969/j.issn.1003-8930.2016.12.004
吴雪颖(1987—),女,硕士研究生,研究方向为电力系统最优化。Email:wuxueying830@163.com
白晓清(1969—),女,博士,副教授,研究方向为电力系统最优化。Email:baixq@gxu.edu.cn
李佩杰(1984—),男,博士,副教授,研究方向为最优化理论在电力系统小干扰稳定中的应用、电力系统稀疏、并行运算。Email:beyondpeijie@163.com
2015-03-02;
2016-02-19
国家重点基础研究发展计划(973计划)资助项目(2013CB228205);国家自然科学基金资助项目(51367004,51407036)
