皮亚诺公理与自然数的序数意义(二)
2016-12-23
皮亚诺公理与自然数的序数意义(二)
张新春
前面说到皮亚诺公理1和公理2,公理1保证了有一个自然数。公理2保证了每个自然数之后都会有一个自然数。这样,看起来会有越来越多的自然数,但事实却不是这样。如果0后面是1,1后面是0,那么这两个数也符合公理1和公理2。为了保证自然数有无限多个,皮亚诺给出了下面的公理:
公理3.0不是任何数的后继数,即对任何自然数n,都有n+≠0。
这条公理保证了不会出现上述周而复始的情况。有了以上三条公理,似乎可以保证有无限多个自然数了,可实际上不是这样。让我们考虑由0、1、2、3、4这5个数组成的数系。我们规定,0+=1,1+=2,2+=3,3+=4,若4+=0,则会进入由0而起的周而复始的状态,上述公理3保证不会出现这个情况。但若4+=1(请注意,这样并没有违背公理3),依然会进入一种周而复始的状态。问题又出现在哪呢?原来是4的后继数与0的后继数一样,从而从侧面切入,又周而复始啦。于是,皮亚诺又准备了以下公理来避免这种情况:
公理4.不同的自然数必有不同的后继数。也就是说,若m,n是自然数,且m≠n,则m+≠n+。等价地说,若m+=n+,则必有m=n。
至此,皮亚诺五公理已经出现了四个,也许你会觉得,这些公理是如此普通,你甚至开始怀疑:这么几条,就能成为现代数学的基础吗?不错,还应该加上一条:
公理5.(数学归纳原理)设P(n)是关于自然数的一个性质,假设P(0)是真的,并假设P(n)是真的,则P(n+)也是真的。那么对每个自然数n,P(n)都是真的。
这里,P(n)指的是一个关于n的性质或命题。举例而言,比如P(n)指的是“n是偶数”或者“n+3比n大”,“2n+1是素数”等。当然,这其中我们还有很多没有定义的概念。我们也可以把P(n)理解为一组编了号的命题。P(0)是第0号命题,P(1)是第1号命题,P(2)是第2号命题……上面的公理是说,如果0号命题是成立的,而且,若第n号命题是成立的,则第n+号命题也是成立的(也就是说第n号后面的一号命题也是成立的),那么所有的命题都是成立的。
公理5还有一个与上述表述完全等价的说法:对于一个集合,若符合以下两点,则这个集合包含所有自然数。
1.这个集合中包含0;
2.若这个集合中包含n,则这个集合中也包括n+。
我们这里说的集合包括0,是指0是这个集合中的一个元素的意思。
这个表述不难理解,由上述第1点,这个集合包括0,而由上述第2点,这个集合又包含0+,即包含1。再重复利用上述第2点,这个集合又应包含1+,即包括2,由此继续。这个公理表明,若是这样的话,这个集合就应该包含所有的自然数。
人们常用多米诺骨牌来说明这个公理。所有的多米诺骨牌都会倒掉,如果满足以下两个条件:
1.最开始的那块会倒掉;
2.若某一块多米诺骨牌倒掉,则紧跟着它的那块也会倒掉。
请你停下来想象一下全部倒掉的多米诺骨牌,再看看公理5,后面有不少概念的定义和不少命题的证明都要用到这个公理。因此,我们在这里应用这个公理证明一个结论,熟悉一下这种应用。(请注意,下
面的证明中,n的后继数n+将被n+1代替)

我们要证明的是,对所有的自然数(这里指大于0的自然数),上述结论都成立。
对自然数1而言,上述结论是指:12=,我们把这个叫做第1号命题。
对自然数2而言,上述结论是指:12+22=,我们把这个叫做第2号命题。
……
对自然数k而言,上述结论是指:12+22+32+…,我们把这个叫做第k号命题。
对自然数k+1而言,上述结论是指:12+22+32+…
于是,我们要证明的是:第1号命题成立,第2号命题成立,第3号命题成立……所有的命题都成立。而根据公理5,要证明这些,我们只要做两件事:
第二件,我们要证明,如果第k号命题成立,那么第k号命题的下一号命题,即第k+1号命题也成立。
第k号命题成立指的是12+22+32+…+k2=。
我们要在此基础上证明第k+1号命题成立,即证明:
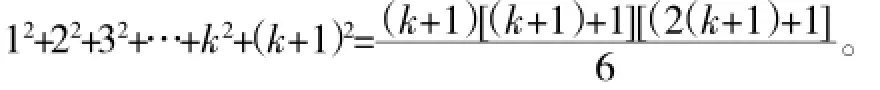
下面就是这个证明过程:

这样,我们就证明了第1号、第2号、第3号……所有这些编好了号的命题都是成立的,也就是对任意的自然数n,以下命题是成立的:12+22+32+…+n2=。
对熟悉数学归纳法的读者而言,以上证明无疑写得冗长而嗦,笔者只是想通过它让不熟悉数学归纳法的读者更容易理解。毕竟相对于书写格式而言,对数学归纳法本质的理解重要得多。
在此,我们将皮亚诺五公理集中写下来:
公理1.0是自然数。
公理2.若n是自然数,则n的后继数也是一个自然数,记作n+。
公理3.0不是任何数的后继数,即对任何自然数n,都有n+≠0。
公理4.不同的自然数必有不同的后继数。也就是说,若m,n是自然数,且m≠n,则m+≠n+。等价地说,若m+=n+,则必有m=n。
公理5.(数学归纳原理)设P(n)是关于自然数的一个性质,假设P(0)是真的,并假设P(n)是真的,则P(n+)也是真的。那么对每个自然数n,P(n)都是真的。
皮亚诺关于自然数的公理体系中有一个重要的概念——后继数。在这个概念下,自然数排好了序。于是,皮亚诺公理体系下的自然数更多的是序数意义。在小学数学引入自然数时,与关注其基数意义一样,也关注其序数意义。如下图所示,在1的基础上增加一个是2,2的基础上增加一个是3……相当于说2是1的后继数,3是2的后继数……

有老师问学生:“自然数有多少个?”学生回答:“无数个。”老师习惯性地(但在这里并不恰当)问:“为什么呢?”有学生回答:“随便哪个自然数的后面总还有自然数,因此自然数数也数不完,有无数个。”这个学生的回答即可以看成是自发地运用了皮亚诺公理。
在皮亚诺公理体系下,我们其实不太在乎第一个自然数叫什么,0或者1都行。所以,0是不是自然数都没有关系(只需把公理1修改一下即可)。而在自然数的基数意义下,0作为自然数的理由更充分,因为这时我们是将自然数定义为有限集合的基数的,而空集自然应该被当成有限集合,其基数当然也应该是一个自然数,只有0适合作为其基数。
