X射线脉冲星光子序列频域加权测相方法

焦荣,许录平,张华,张娇

(西安电子科技大学空间科学与技术学院,710126,西安)



X射线脉冲星光子序列频域加权测相方法

焦荣,许录平,张华,张娇

(西安电子科技大学空间科学与技术学院,710126,西安)

针对X射线脉冲星信号累积轮廓位相测量误差大的问题,提出了一种直接位相测量的频域加权方法。首先,直接对X射线探测器捕获和采样形成的光子序列进行频域变换得到幅度谱,分别提取幅度谱各个成分的相位,再用幅度对相位变量加权平均,得到位相测量结果;进一步采取分段加权的策略,解决序列过长引起的内存溢出问题;最后对所提出方法的计算复杂度进行了理论分析。仿真结果表明:在观测时长和采样间隔相同的条件下,与平均法相比,加权法的测相精度提高了10%以上;与最大似然(ML)和非线性最小均方误差(NLS)法相比,加权法的比相精度提升了1倍以上,计算速度处于ML法和NLS法之间;分段情况下性能会随着分段数增加有所改善。

X射线脉冲星;位相测量;快速傅里叶变换;最大似然

脉冲星是一种高速稳定自旋的中子星,其旋转轴和辐射轴不重合,当探测器处于其辐射扫描区内时,能够收到稳定的周期性的脉冲信号,利用该信号计时可以实现基于脉冲星的航天器导航。由于利用X射线信号有利于探测器小型化,因此X射线脉冲星导航已成为具有潜力的航天器导航方法,它通过测量脉冲星信号到达航天器和某一选定惯性参考点之间的相位差来获取航天器相对于坐标中心的位置信息[1-3]。其中,相位测量的误差直接影响导航定位精度,因此相位测量技术是影响脉冲星导航性能的关键技术之一。

X射线脉冲星信号的测量技术大致可以分为两类,一类是基于脉冲星信号累积轮廓的位相测量方法[1,4-5],另一类是直接对光子序列的初相进行测量[3,6]。基于累积轮廓的位相测量方法又分为时域方法[7-8]、频域方法和其他变换域方法,基于这几种方法又延伸出了若干改进方法如双谱变换[9]和基于小波变换的轮廓测相等[3,6,10];光子序列初相测量以最大似然方法为主,根据模型的不同,也发展了一些改进的方法[3,6]。从实际信号处理过程来看,基于时域的周期估计算法耗时长,频域方法及其改进方法[4-5,7-9]往往能在不显著增加计算量的前提下获得更高的精度,但这些方法一般都需要先累积出轮廓,而轮廓的累积过程受到脉冲星周期误差、演化模型等多种因素的影响,这些因素会直接导致轮廓存在相移[11]和畸变,从而增加了测量误差。因此,从位相测量的角度,直接对光子序列测相,可以避免轮廓累积的过处理引入的附加误差,从而精度更高。已有文献表明,针对光子序列的最大似然方法有能力获得更高的精度[6]。Zhang等人提出的基于轮廓模型的最大似然方法[3]存在以下不足:①需对每个光子求解代价函数并搜索,计算量大;②最大似然对信号光子和噪声光子的处理方法相同,对信号、噪声以及不同的轮廓成分并不加区分。因此,本文提出基于快速傅里叶变换(FFT)的X射线脉冲星光子序列位相测量的频域加权方法。基本思想是:通过频域变换和加权,使强度不同的成分对测量精度的贡献不同。此外,由于背景辐射噪声具有较宽、较平坦的频谱,在频谱加权方法中的权重较小,其对相位测量精度的影响能被一定程度的抑制。

1 信号模型

脉冲星的脉冲信号具有稳定的周期,如果已知t0时刻的初相φ0、频率f以及频率的多阶导数f(m),太阳系质心(SSB)处的相位可以利用相位演化模型精确预测[12]

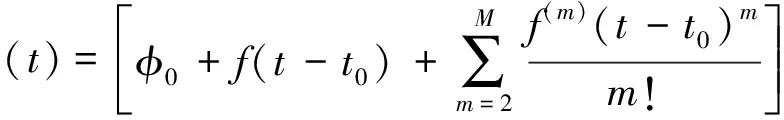
(1)

式中:φ(t)表示t时刻的相位;[·]表示取余数操作,定义为[φ]=int(φ)+mx,mx∈[0,1),int表示取整,[·]保证相位始终为[0,1)的实数;M为整数;通常,f(m)(m≥2)非常小(10-12～10-19),脉冲星在数小时甚至几天内可以近似认为是等周期的,周期为1/f。由于脉冲星的轮廓结构具有多样性,因此在频域可以看到明显的谱线。本文选择具有稳定的周期特性的X射线脉冲星作为导航的参考基准。

实际信号强度非常微弱,被认为是以光子形态顺序到达探测器的,再经过X射线探测器捕获和采样形成光子序列,又由于到达SSB处脉冲星信号的周期特性,因此常用非齐次循环平稳泊松过程对X射线脉冲星信号建模[13-14]。

2 频域加权比相

2.1 信号获取

X射线脉冲星信号的位相测量是脉冲星导航的基本测量量[15-18],由于导航方式的不同,位相测量的对象也有不同。在绝对形式的导航中,探测器测量到的脉冲星信号与标准信号演化模型进行相位比对;在相对形式的脉冲星导航中,同一探测器在不同时段获得的同一脉冲星信号之间,或者不同探测器在不同轨道位置探测的同一脉冲星信号之间进行相位比对。在绝对导航方式中,由于任意时刻的标准信号演化模型是不变的,因此在不同时刻脉冲星信号与标准信号演化模型的比对,可以等效于探测器在不同时刻探测的信号之间的相位比对。所以,本文以相对形式导航为背景,对相位测量方法进行阐述。

2.2 频域加权比相

加权FFT相位估计的基本思路是:两路光子序列来自同一颗脉冲星的信号,对两列光子流量序列进行FFT变换,对其每个频域点求相位,再对两列信号对应频点相位做差运算后加权平均,得到延迟相位估计值。令两路比相序列分别为G1和G2,加权FFT比相方法示意图如图1所示。

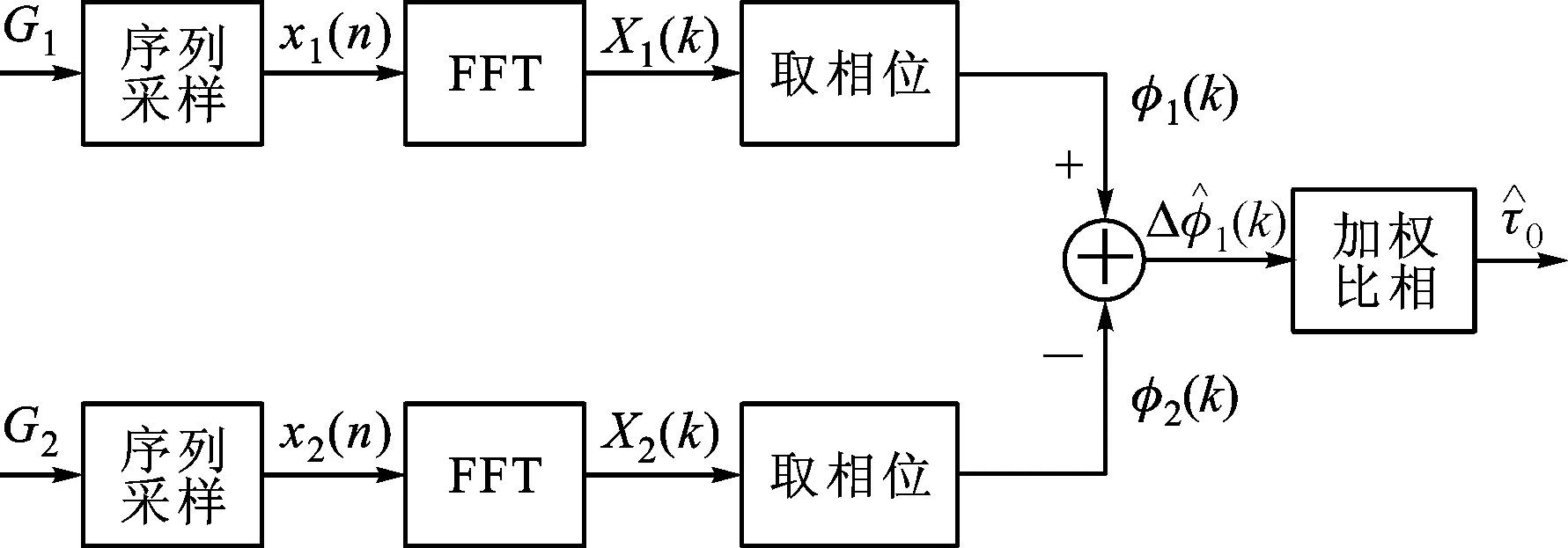
图1 加权FFT比相方法示意图

两路光子序列来自同一颗脉冲星,经过等间隔采样分别得到采样后序列x1(n)、x2(n),其中n为整数,n∈[0,N],N为序列长度,且有N=NbNp,Np为观测时间内的脉冲周期个数,Nb代表单周期内包含的采样点数。设定x2(n)相比于x1(n)延迟相位τ0,即x2(n)=x1(n-τ0)+γ,其中γ为白噪声,如果暂时不考虑整周期模糊度问题,有τ0∈[0,Nb],则有两光子序列的N点FFT分别为

(2)

X2(k)=fft[x2(n)]=fft[x1(n-τ0)+γ]=

(3)

式中:fft[·]表示傅里叶变换;fft[γ]为常数。分别提取X1(k)、X2(k)对应频点相位值进行做差运算,可以得到k频点相位差为

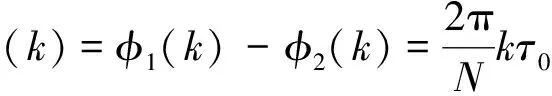
(4)

式中:φ1(k)、φ2(k)分别为k频点对应的相位。容易得到归一化的k频点脉冲星的相位差

(5)

(6)

式中:w(k)为权值,其计算式为

(7)

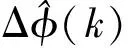
(8)

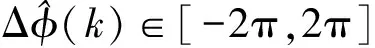
(9)

2.3 分段式频域加权比相

当信号序列较长时,FFT变换可能导致计算机内存溢出,因此本文提出分段式频域加权比相方法。

设长序列{λ(1),λ(2),…,λ(N)}为单位时间片段Tb(周期内最小采样间隔时间长度)内的光子数量。为便于FFT计算,将光子强度序列分为L段,令I=1,2,…,L,表示第I段,每段均包含相同的整数个周期长度,其中每段含M个样点,即N=LM。若为了获得适合FFT算法的长度,可对每段数据进行补零运算。

相应地,两光子强度序列的相位差为

(10)

式中:φI,1(k)、φI,2(k)分别为序列1及序列2在第I段的相位。两光子的延迟相位值为

(11)

令sI(k)=ΔφI(k)/k,则有

(12)

(13)

式中:k=1,2,…,M。平均所有数据段的相位延迟估计值,即可得到长序列的相位延迟估计值为

(14)

理论上,本文方法性能优势体现在:①从式(8)和式(10)可见,频域方法不需要采样时间间隔,其测量相位是连续的;②X射线背景噪声流量恒定,通常可认为服从均匀分布,当光子数较多时,其幅度谱一般可近似为常值[14],信号的周期性使其谱线幅度明显高于噪声,因此本文通过引入幅度权重使噪声对相位测量的影响得到抑制,相比而言,NLS和ML法对待噪声和信号是等同的。

2.4 计算复杂度分析

计算复杂度是指对用于比相估计的算法所采用的加、减、乘、除的总运算次数的分析。假定观测时间Tobs内约有Np个脉冲星周期P,则有Tobs≈NpP。对该段观测时间进行等间隔采样,则每间隔长度为Tb,Nb代表一个周期内包含的时间片段数,则有Tb=P/Nb。

采用加权FFT法进行比相估计,需要对两列光子序列进行FFT变换,频域内的相位值作差,累积,最后对所得到的能量加权。因此,完成加权FFT比相估计总共需要(NbNp)2+6NbNp步运算过程。

分段加权FFT运算主要使在FFT变换处的计算代价得到了极大的节省。假定观测时间内的Np个周期被分成了L段,每段包含K(K≪N)个周期,则分段加权FFT总共需要L(NbK)2+6NbNp步运算。

[6]中NLS方法和参考文献[3]中ML方法的计算量与本文方法作比较,如表1所示。

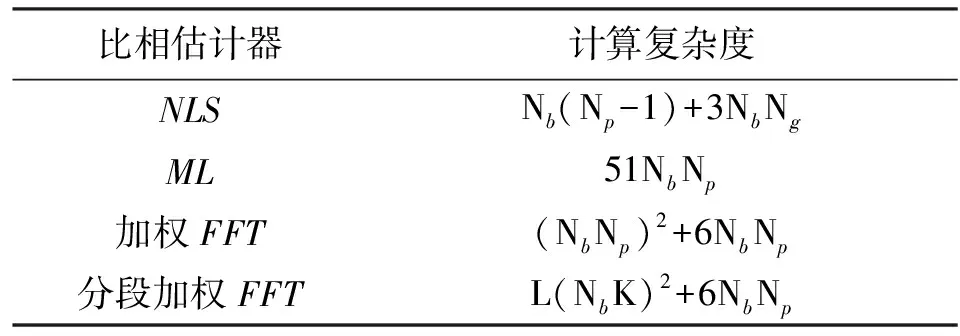
表1 NLS、ML、加权FFT及分段加权FFT方法 的计算复杂度比较

注:Ng表示将归一化相位区间(0,1)分为Ng段。

可见,加权FFT法的计算复杂度介于NLS法与ML法之间。此外,分段加权FFT法使一次FFT变换的实际数据量得到了极大的缩减,从而实现了计算复杂度的进一步改善。

3 仿真结果与分析

本实验采用RXTE探测器探测到的蟹状脉冲星PSR B0531+21数据作为分析对象。B0531+21脉冲星的周期为33.4 ms,RXTE探测器的有效面积为6 800 cm2;X射线源发射的光子序列及探测器的背景噪声主要由高斯模型和泊松模型拟合生成[14],该方法将脉冲星轮廓用高斯函数拟合,然后结合信号光子和噪声密度计算探测器单位采样间隔内探测到的总流量强度,并作为泊松分布的参数,进而模拟生成光子序列。仿真中设置光子流量密度为0.96 ph/(cm2·s)(软X射线能段),背景噪声密度为0.45 ph/(cm2·s)。软件平台为Matlab R2012a,计算机配置为:Intel(R)Core(TM)i5-3470 CPU@3.20 GHz,内存为4.00 GB(3.47 GB可用),操作系统为Window 7专业版。

3.1 均方根误差对比分析

比相估计的均方根误差主要用于反映比相估计值偏移真值的程度,其计算公式为

φ0)2])1/2

(15)

在测试过程中,设定观测时间为0.1～1 000 s,采样间隔Tb为P/1 024 s(P为脉冲星周期,此处为33.4 ms)。实验过程中相位是按(0,1)归一化。采用蒙特卡罗方法进行多组随机仿真,得到NLS、ML及加权FFT方法估计的比相均方根误差随观测时间的变化曲线如图2a所示。

由图2a可以看出:随着观测时间的增加,这3种方法估计的比相均方根误差均呈现逐渐减小的趋势,其中NLS和ML算法估计的均方根误差基本在相同的数量级水平变动,而加权FFT方法比前两者估计出的均方根误差要明显低,即其比相精度要明显高于NLS和ML算法。

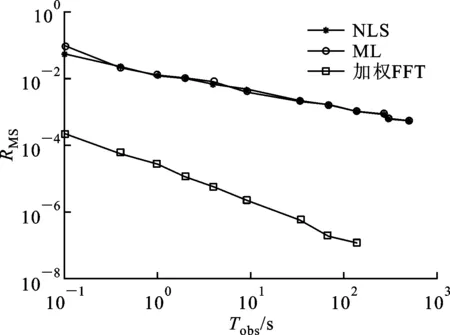
(a)均方根误差曲线

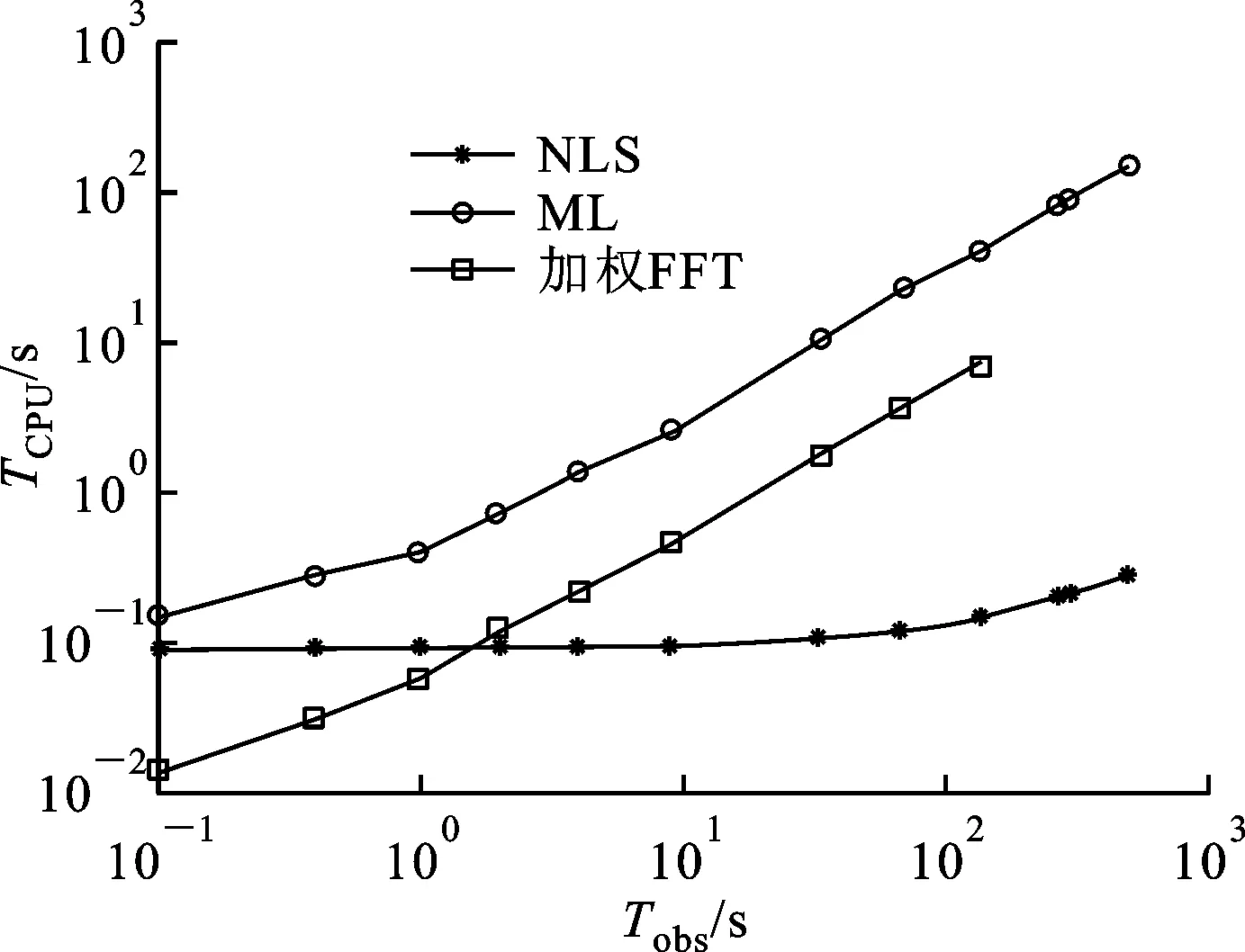
(b)CPU时间曲线图2 NLS、ML及加权FFT法的比相估计对比

由于频域内两光子强度序列间的相位差与对应频点的比值在每个频率值处均对应一个比值,这些比值十分接近,因此可反映出时域内的相移量。为了准确获得时域内的相移,需要对这些比值进行处理,一般可通过平均法或加权法来得到一个稳定的比值。基于平均法和加权法对这些比值处理后得到的相移误差如图3所示。加权法赋予有效光子信号更大的比值,而平均法则对有用信号和噪声信号进行了等比重处理,由图3可见,加权法较平均法得到的测相误差更小。

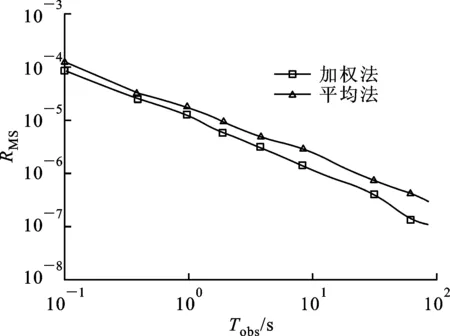
图3 平均法和加权法的测相误差对比图

3.2 计算时间对比分析

NLS、ML及加权FFT方法比相估计的计算代价主要考察各方法仿真占用CPU时间。其中,NLS法的总CPU时间主要由轮廓累积、完成非线性最小均方估计及完成抛物插值运算所需的时间构成;ML法的总CPU时间主要由最大似然函数模型搭建及插值运算所需的时间构成;加权FFT法的总CPU时间主要是FFT变换和相位累积及加权所需的时间总和。图2为比相估计所需的总CPU时间。由图可知,随着观测时间的延长,NLS法使用CPU时间呈现缓慢增长的趋势,ML和加权FFT法所用CPU时间均呈现显著增长的趋势,但ML法比加权FFT法使用的CPU时间要长约10倍左右。可见,在计算代价方面,随着观测时间的延长,加权FFT算法的计算代价介于NLS与ML算法之间,且相比于ML算法要明显省时。

3.3 分段加权FFT与加权FFT方法

3.3.1 观测时间及采样间隔对加权FFT比相测量精度的影响 在不同的观测时间(Tobs)和采样间隔(Ts)条件下,进一步验证它们对加权FFT法比相测量精度的影响。实验采取控制变量的方式及蒙特卡罗法对多组[0,0.5]范围内随机相位进行了测试。通过实验,得到在不同观测时间和采样间隔条件下的加权FFT比相的均方根误差分布图,如图4所示。从图4可以看出:在一定的采样间隔下,当观测时间逐渐延长时,加权FFT法的比相精度逐渐提高;在一定的观测时间下,对观测到的脉冲星序列进行不同采样间隔的采样,当采样数逐渐增大时,加权FFT的比相精度随之提高。可见,在一定的观测时间和采样间隔变化范围内,脉冲信号的观测时间越长,采样间隔数越多,加权FFT算法估计出来的比相值越接近真实值,但当观测时间和采样间隔足够大时,加权FFT法比相精度不再明显受这两个变量的影响而逐渐趋于稳定。

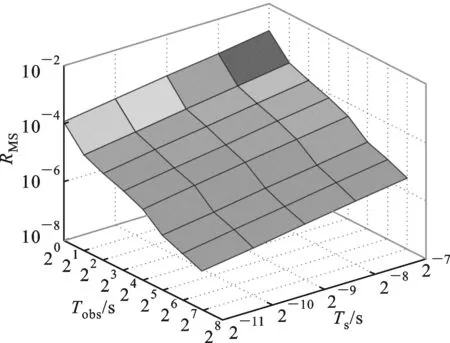
图4 加权FFT法在不同观测时间和采样间隔下的均方根误差二维分布图

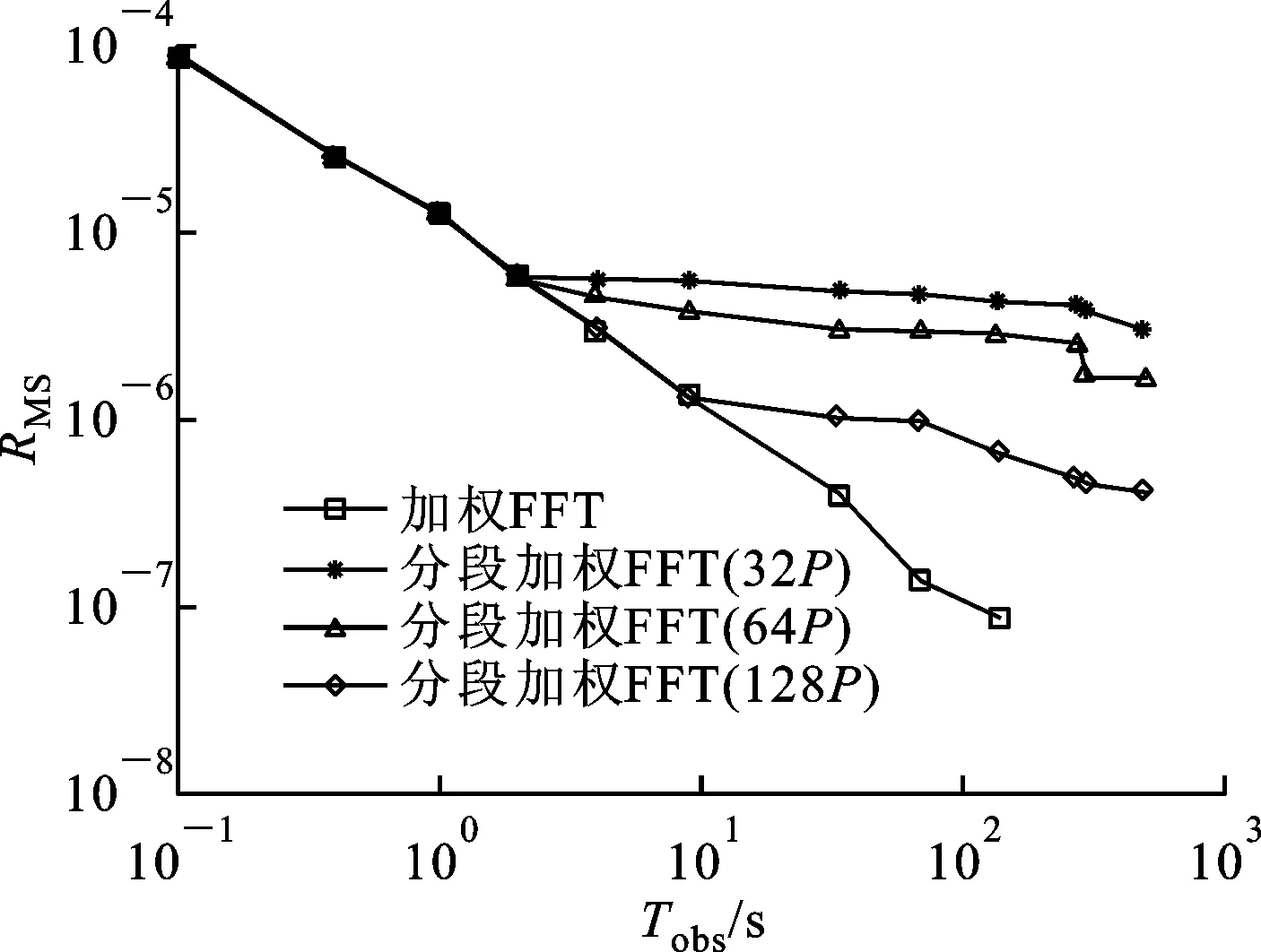
3.3.2 加权FFT法和分段加权FFT法比相的RMS、计算代价的对比分析 分段加权FFT法的比相精度仍然从均方根误差和计算代价两方面进行测试及验证。实验中,分别以相同观测时间内32个周期、64个周期及256个周期为分段区间长度进行测试,结果如图5所示。

(a)均方根误差曲线

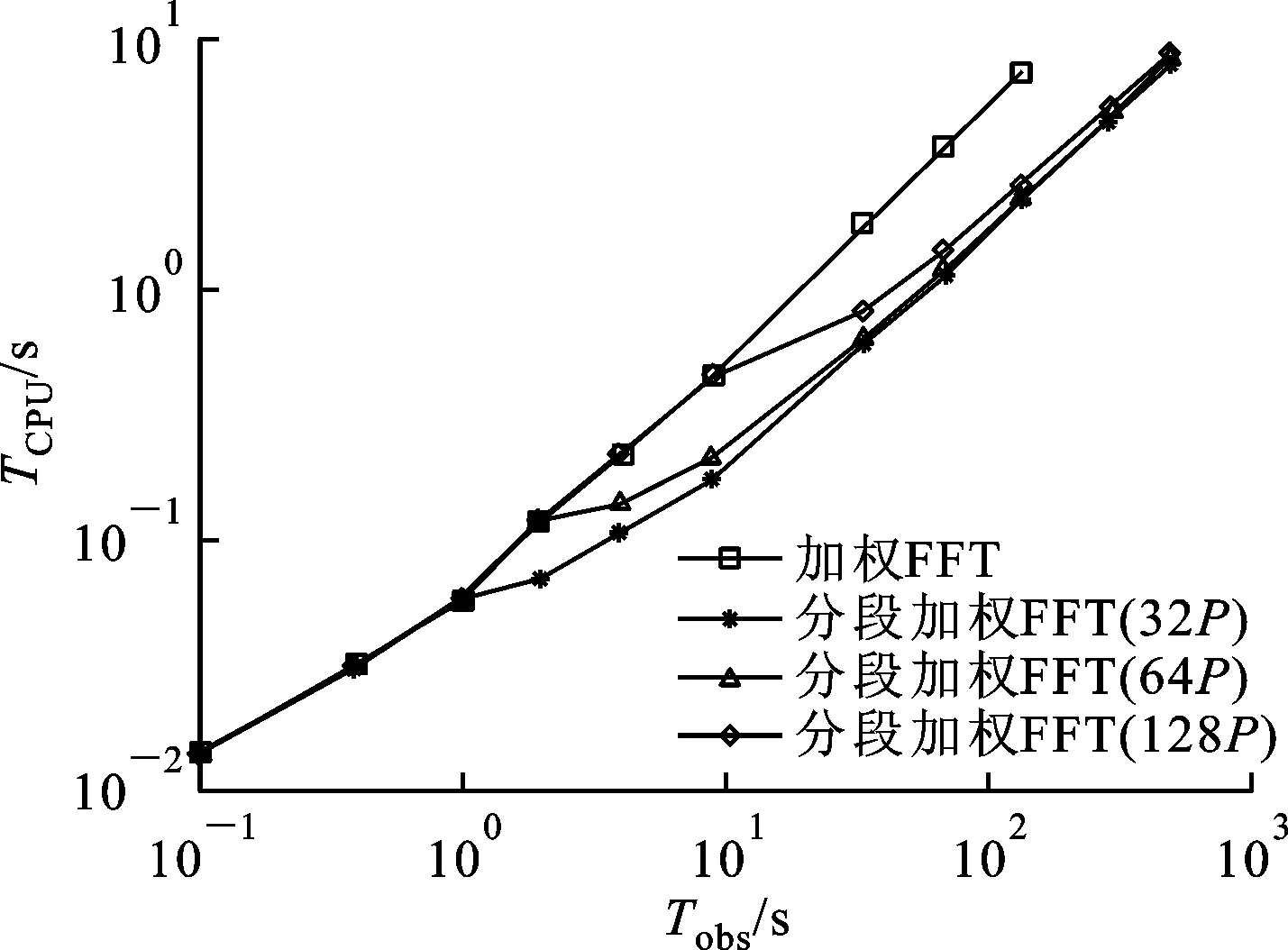
(b)CPU时间曲线图5 加权FFT法在不同分段长度下的比相估计对比图

由图5a可以观察到:初始时刻,分段加权FFT法比相的均方根误差几乎与该小段时间内进行加权FFT法比相的均方根误差接近,但随着观测时间的延长,均方根误差会缓慢下降,虽然下降的速度明显要低于加权FFT法的比相,总体上来说仍然高于ML和NLS法。由图5b可以看出,随着观测时间的延长,分段加权FFT法的CPU时间仍然保持增长趋势,但明显要少于加权FFT法。此外,加权FFT法在140 s左右的观测时间处出现了内存溢出的现象,无法继续进行比相估计,而分段加权FFT法仍然可以实现比相,可有效解决内存溢出问题。

4 结 论

针对脉冲星导航中的比相问题,本文提出了频域加权方法。该方法考虑了X射线信号频率成分对测相贡献上的差异,对不同的频率成分,根据强度赋予不同的权值,适用于基于脉冲星的相对导航以及相位增量测量等应用。仿真结果表明,本文的频域加权法在测相精度上优于平均法、NLS和ML方法,计算复杂度介于NLS和ML方法之间。分段频域加权后,性能有所下降,但可以克服序列过长引起的内存溢出问题,从而可以适应内存受限的计算系统。

参考文献:

[1] SHEIKH S I. The use of variable celestial X-ray sources for spacecraft navigation [D]. Maryland, MD, USA: University of Maryland, College Park, 2005.

[2] LIU Jing, MA Jie, TIAN Jinwen, et al. X-ray pulsar navigation method for spacecraft with pulsar direction error [J]. Advances in Space Research, 2010, 46(11): 1409-1417.

[3] ZHANG Hua, XU Luping, SHEN Yanghe, et al. A new maximum-likelihood phase estimation method for X-ray pulsar signals [J]. Journal of Zhejiang University: Science C, 2014, 15(6): 458-469.

[4] RINAURO S, COLONNE S, SCARANO G. Fast near-maximum likelihood phase estimation of X-ray pulsars [J]. Signal Processing, 2013, 93(1): 326-331.

[5] ZHANG Hua, XU Luping. An improved phase measurement method of integrated pulse profile for pulsar [J]. Science China Technological Sciences, 2011, 54(9): 2263-2270.

[6] EMADZADEH A A, SPEYER J L. On modeling and pulse phase estimation of X-ray pulsars [J]. IEEE Transactions on Signal Processing, 2010, 58(9): 4484-4495.

[7] 李建勋, 柯熙政. 基于循环平稳信号相干统计量的脉冲星周期估计新方法 [J]. 物理学报, 2010, 59(11): 8304-8310. LI Jianxun, KE Xizheng. Period estimation method for weak pulsars based on coherent statistic of cyclostationary signal [J]. Acta Physic Sinica, 2010, 59(11): 8304-8310.

[8] 李建勋, 柯熙政, 赵宝升, 等. 一种脉冲星周期的时域估计新方法 [J]. 物理学报, 2012, 61(6): 069701. LI Jianxun, KE Xizheng, ZHAO Baosheng, et al. A new time-domain estimation method for period of pulsars [J]. Acta Physica Sinica, 2012, 61(6): 069701.

[9] 谢振华, 许录平, 倪广仁, 等. 基于双谱的脉冲星累积脉冲轮廓时间延迟测量 [J]. 物理学报, 2008, 57(10): 6683-6688. XIE Zhenhua, XU Luping, NI Guangren, et al. Time offset measurement algorithm based on bispectrum for pulsar integrated pulse profiles [J]. Acta Physic Sinica, 2008, 57(10): 6683-6688.

[10]阎迪, 许录平, 谢振华, 等. 脉冲星信号模糊阈值小波降噪算法 [J]. 西安交通大学学报, 2007, 10(41): 1193-1196. YAN Di, XU Luping, XIE Zhenhua, et al. Wavelet denoising algorithm based on fuzzy threshold for pulsar signal [J]. Journal of Xi’an Jiaotong University, 2007, 41(10): 1193-1196.

[11]ZHANG Hua, XU Luping, XIE Qiang, et al. Modeling and Doppler measurement of X-ray pulsar [J]. Science China Physics, Mechanics and Astronomy, 2011, 54(6): 1068-1076.

[12]TAYLOR J H. Pulsar timing and relativistic gravity [J]. Philosophical Transactions of the Royal society of London: Series A Physical and Engineering Sciences, 1992, 341(1660): 117-134.

[13]SALA J, URRUELA A, VILLARES X, et al. Feasibility study for a spacecraft navigation system relying on pulsar timing information: ARIADNA Study 03/4202 [R]. Barcelona, Spain: European Space Agency Advanced Concepts Team, 2004.

[14]ZHANG Hua, XU Luping, SONG Shibin, et al. A fast method for X-ray pulsar signal simulation [J]. Acta Astronautica, 2014, 98(5): 189-200.

[15]SHEIKH S I, PINES D J, RAY P S, et al. Spacecraft navigation using X-ray pulsars [J]. Journal of Guidance Control and Dynamics, 2006, 29(1): 49-63.

[16]XIONG Zhi, QIAO Li, LIU Jianye, et al. GEO satellite autonomous navigation using X-ray pulsar navigation and GNSS measurements [J]. International Journal of Innovative Computing, Information and Control, 2012, 8(5): 2965-2977.

[17]BERNHARDT M G, PRINZ T, BECKER W, et al. Timing X-ray pulsars with application to spacecraft navigation [C]∥Proceedings of High Time Resolution Astrophysics IV. Garching, Germany: Institute of Astronautics, 2010: 1-5.

[18]ASHBY N, HOWE D A. Relativity and Timing in X-ray pulsar navigation [C]∥Proceedings of 2006 IEEE International Frequency Control Symposium and Exposition. Piscataway, NJ, USA: IEEE, 2006: 767-770.

(编辑 刘杨)

A Frequency Domain Weighted Measurement Method for X-Ray Pulsar Photon Sequences

JIAO Rong,XU Luping,ZHANG Hua,ZHANG Jiao

(School of Aerospace Science and Technology, Xidian University, Xi’an 710126, China)

A weighted direct phase estimation algorithm in frequency domain for photon sequence is proposed to solve the problem that the error of accumulated phase estimation in the average profile is too large for X-ray pulsar signals. The photon sequence that is captured by the X-ray detector and then sampled is directly transformed to the frequency domain, then the phase of each frequency is respectively extracted and is weighted according the amplitude of the frequency component. Furthermore, the segmented fast Fourier transform strategy is adopted to solve the memory overflow problem caused by long sequences. Finally, the computational complexity of the proposed estimator is investigated in theory. Simulations and comparisons with existing methods under the condition of the same observation time and sampling interval show that the accuracy of the weighted approach increases by 10% over the average method and is two times higher than those of the nonlinear least square (NLS) and maximum likelihood (ML) methods, and that the computational complexity of the algorithm is between NLS and ML methods. Moreover, the performance of the algorithm with segments is improved by increasing the number of segments.

X-ray pulsar; phase estimation; fast Fourier transform; maximum likelihood

2015-12-17。 作者简介:焦荣(1983—),女,博士生;许录平(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61172138,61401340)。

时间:2016-04-03

10.7652/xjtuxb201606023

P128.4

A

0253-987X(2016)06-0152-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160403.1820.004.html