一种采用交流激励的微弱非线性电流-电压关系测试方法

何鋆,白春江,王新波,白鹤,胡天存,崔万照,刘纯亮

(1.中国空间技术研究院西安分院空间微波技术重点实验室,710100,西安;2.西安交通大学电子与信息工程学院,710049,西安)



一种采用交流激励的微弱非线性电流-电压关系测试方法

何鋆1,2,白春江1,王新波1,白鹤1,胡天存1,崔万照1,刘纯亮2

(1.中国空间技术研究院西安分院空间微波技术重点实验室,710100,西安;2.西安交通大学电子与信息工程学院,710049,西安)

为解决射频及微波接触部件无源互调机理研究中直流模式无法在强线性背景中测量到微弱的非线性电流电压关系这一问题,提出了一种新的基于交流激励的测试方法。首先通过理论推导得到了具有微弱非线性特性的部件在交流电压激励下的电流电压关系表达式;然后根据该方法对由同一个二极管并联不同电阻组成的样品进行了测试,通过测量各阶谐波的信号幅度并进行相关计算,得到了强的线性项和非线性项的系数,进一步根据推导出的公式计算得到了样品的电流电压曲线和来自于二极管的电流电压曲线的非线性部分。测试和计算结果表明:该方法能够获得比线性部分低3～4个数量级的非线性部分电流,这是传统的直流方法无法测量到的;对不同样件计算所得的来自同一二极管的电流电压曲线的非线性部分是相等的,证实了该方法测量强线性背景中弱的非线性电流电压关系的可行性。该方法可为无源互调非线性机理的研究提供新的测量手段。

无源互调;非线性;电流电压;谐波

在通信系统中,当频率分别为f1和f2的两路信号通过具有非线性导电行为的部件时,会产生无源互调(Passive Intermodulation,PIM),PIM产物的频率为nf1±mf2(n,m≥1,为正整数)。在一些发射和接收单元距离较近且需要同时工作的通信系统中,发射机产生的PIM产物极有可能会落入接收通道并对系统形成干扰。此外,在一些大功率的通信系统中,也很容易出现PIM问题。随着技术的进步和需求的提高,发射机的功率越来越大,接收机的灵敏度也越来越高,随之而来的PIM问题也急需解决。由于PIM对通信系统的影响重大,因此在过去几十年中,世界各国的研究者对PIM问题已经开展了大量的研究工作[1-10],其中一个很重要的方面就是通过研究其产生的物理机理来对设计和制造低PIM部件提供指导[11-15]。研究发现,PIM通常来自于具有非线性导电特性的材料或不理想的金属接触[1-3]。现在已经知道,铁磁材料产生的PIM电平要比金属接触的高几个数量级,因此在无源部件中要避免使用铁磁材料[2]。对于金属接触,其实际的物理机理极为复杂,是PIM机理研究的一个难点。许多文献指出[11-14],导致接触非线性的可能来源有:与界面灰尘相联系的电击穿,金属结构中的微孔和狭缝处的微放电以及绝缘层的隧穿效应等。然而,在这些可能的物理机理中只有隧穿效应在实验上被Bond等人证实了,但是他们使用的是专门制作的Al-Al2O3-Al结[12],本身就具有强的非线性导电特性,这和实际具有金属接触结构部件的导电特性有很大的不同。

通常用直流方式测量诸如同轴接头、编织电缆和波导结等具有金属接触结构部件的电流-电压(I-V)关系时,结果显示是线性的,因此它们通常被认为是线性部件。但是,在通信领域,当功率足够高的两路信号通过此类部件时,会产生强度比载波低非常多的互调产物(此即互调测试),这表明它们具有微弱的非线性导电特性。虽然互调测试这一方法能够检测到许多不同系统的非线性响应[16-17],但是却难以直接揭示导致非线性出现的物理机理。对PIM的产生机理即非线性的产生机理进行研究,最直接的方法是测量部件的非线性I-V关系,根据I-V关系的特性判断物理机制,此外针对接触结构非线性建模的正确与否也需要通过测量相关部件的I-V关系来证实。由于部件的非线性很弱,且叠加在强的线性背景中,常用的直流测试手段和方法并不能够测量到非线性,至今还未见到实际部件非线性I-V关系测量方面的报道,这也是研究接触结构PIM产生机理的难点之一。针对直流方式难以测量到通常被认为是线性部件的微弱非线性I-V特性这一问题,本文提出了一种基于交流模式的测试方法,并推导出了相应的I-V关系式。通过对以二极管和电阻组成的样件进行实际测试,得到了强线性背景中弱的非线性I-V特性,这为通过直接测量和分析部件的非线性特性来研究与其对应的物理机理提供了一种新方法和新途径。

1 交流激励模型

通常情况下,金属接触结构的导电特性是欧姆型的,即是线性的,但是通信领域中PIM产物的出现表明其具有微弱的非线性导电特性。这可能是由一个或几个非线性的物理机理导致的,如隧穿效应、热电子发射、微放电和电击穿等[11-14]。基于这些考虑,具有金属接触结构部件的I-V关系可以用幂级数表示

I=G1V+G2V2+…+GnVn+…

(1)

式中:I是流过部件的电流;V是加在部件上的电压;Gn是第n次项的系数。式(1)中线性项即第一项主要是欧姆导电机理的贡献,而非线性的导电机理对各项都有贡献。当用直流模式来表征部件的I-V关系时,通常是将部件与电压(或电流)源相连,并测量相应的电流(或电压)。以连接电压源为例,根据式(1),测量到的电流是线性项与非线性项之和。对于实际部件,因为G1通常要比Gn(n≥2)大几个数量级,因此线性项主导着I-V特性。直流情况下要得到非线性项,需要根据式(1)来对测得的I-V曲线进行拟合。因为非线性部分极有可能低于仪器的分辨率,所以非线性部分项会被丢失,拟合结果的可靠性难以保证。综合这些分析,直流模式难以准确测量到实际部件微弱的非线性部分。

要测量实际部件弱的非线性部分,需要将其与强的线性部分分离,这可以用交流模式实现。若给试件施加交流电压,其响应与加直流电压时有很大不同。当所加交变电压V=V0cosωt时,根据式(1),电流可表示为

I=G1V0cosωt+G2V02cos2ωt+…+

GnV0ncosnωt+…

对于cosnωt,利用二项式定理有

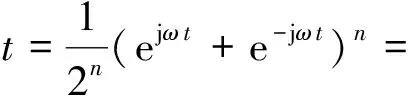
(2)

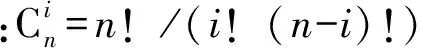
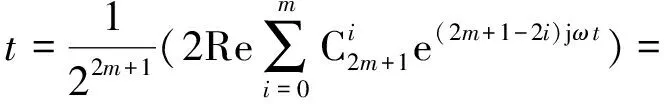
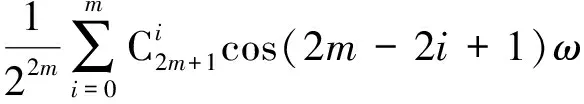
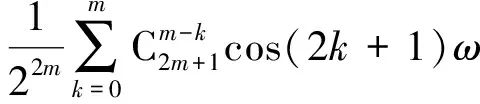
(3)

当n为偶数,即n=2m(m≥1)时,式(2)可写成

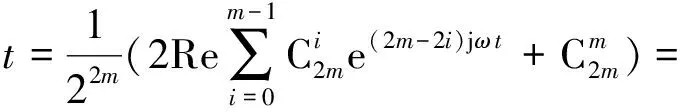
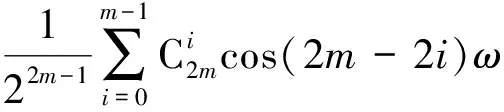
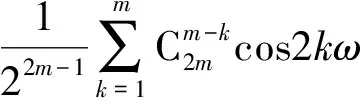
(4)

结合式(2)～(4),加交变电压时的电流为

(5)

如果Gn≫Gn+2,对某一固定的频率项,即k值固定时,后半部分求和中只需考虑m=k这一项,m>k的项可以忽略不计。因此,式(5)可近似为

t+

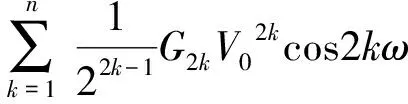
(6)

这里虽然假设Gn≫Gn+2,但即使条件不满足,对某一固定的频率项,即k值固定时,式(5)后半部分求和的数值(可测量值)总是能用一个系数G2k+1或G2k表示,因此式(5)总是能简化为式(6)。在这种情况下,式(6)中的Gn与式(1)中的Gn不再一一对应。由式(6)可知,当施加交变信号时,部件的非线性特性会产生谐波,最主要的是线性项与非线性项会在频率空间发生分离。这和直流模式下的情况很不同,测量弱的非线性项时将不受强的线性项的影响。当用低频的交流信号来测量微弱的非线性时,几十cm的测试连线长度相比于基波信号的波长完全可以忽略(以100 kHz交变电压信号为例,其波长为3 000 m),因此可以沿用直流电路的相关理论如分压原理等。受限于电路的寄生参量和沿用直流的电路连接方式与相关理论,所采用的交流信号的频率有上限,不能超过1 MHz。借助于具有高动态范围的低频测量仪器——锁相放大器,通过测量谐波信号可以得到相应的非线性项。为了进行验证,本文选取二极管和电阻为研究对象,开展了相应的实验。

2 实验、结果及讨论

2.1 电路连接

图1所示的是本文采用的谐波测试电路连接图。当具有一定频率的交流电压经通道2加在测试件(DUT)上时,由于DUT具有一定的非线性导电特性,因此会产生谐波。谐波信号会在采样电阻R上产生压降,该压降可由通道1进行测量,采样电阻阻值为51 Ω。实验选用Standford SR830型锁相放大器作为交流电压源来激励DUT,并同时用它测量谐波信号。锁相放大器的主要参数如下:灵敏度为2 nV;输入阻抗为10 MΩ;动态范围大于100 dB;谐波失真为-80 dB;频率范围为1 mHz～102 kHz;输出阻抗为50 Ω。为了展示和验证用交流方式测量非线性的可行性,用一个二极管并联一电阻作为DUT,测量时交流激励电压的频率为878 Hz。

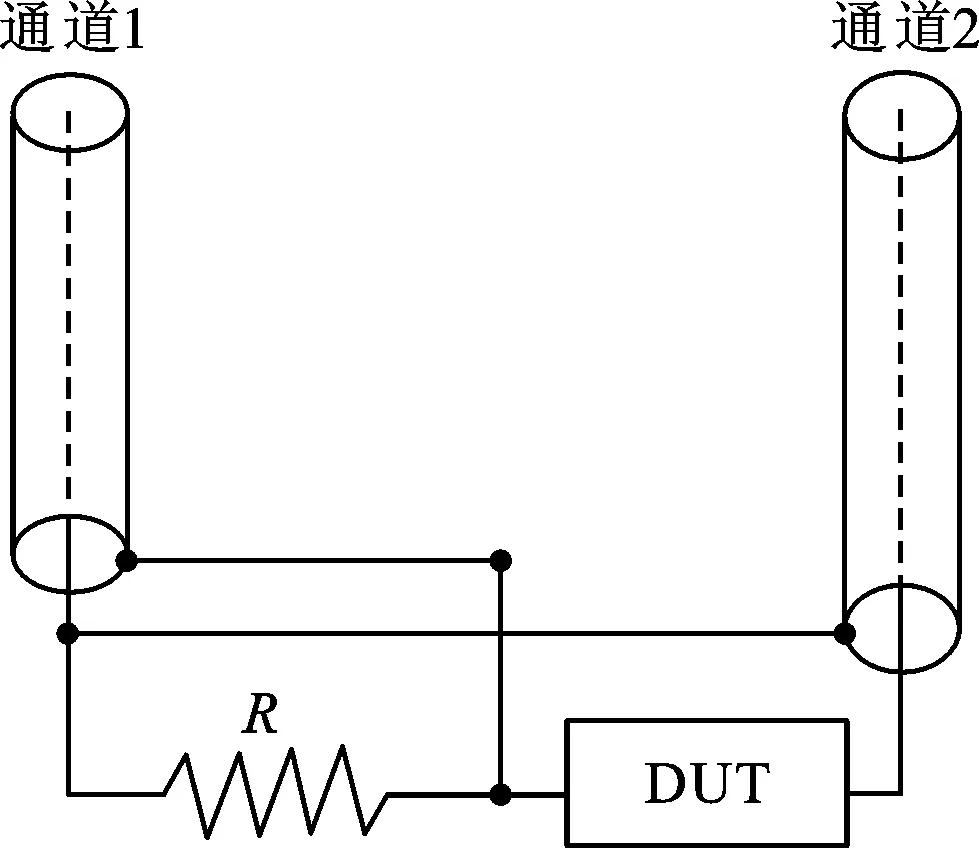
图1 谐波测试电路连接图

2.2 测量结果

图2展示了谐波信号的振幅(有效值)随激励信号振幅(有效值)的变化关系,DUT由二极管并联一阻值约为10 kΩ的电阻组成(DUT1)。从图2可以看出:对于1～5次谐波,在0～130 mV区间,其振幅随着激励信号振幅的增加而增加;对于更高次的谐波,振幅在低电压区域振荡,在高电压区随着激励信号幅度的增加而增加。此外,谐波信号的振幅随着其阶次的增大而降低。高次谐波在低电压区振荡的原因是其振幅接近或低于仪器的测量极限,易受到系统噪声和信号源谐波失真的影响。考虑到此因素,最高只测量到第9次谐波。

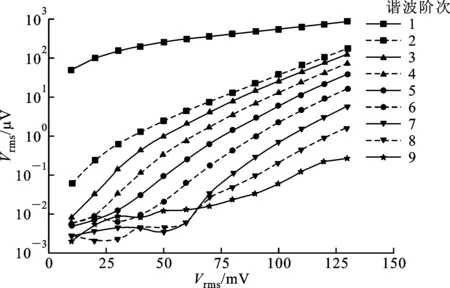
图2 谐波信号振幅随交流激励信号振幅的变化关系

2.3 DUT的I-V关系

既然谐波的振幅随激励信号振幅的变化关系已经得到,通过计算便可获基波和各高阶谐波的I-V曲线,需要注意的是由于信号源内阻和采样电阻的存在,激励信号的电压并没有全部加在DUT上。在获得基波和各高阶谐波的I-V关系后,根据式(6)就可以计算得到线性项和各阶非线性项的系数,并进一步计算得到DUT的I-V关系。表1中列出了线性项和各阶非线性项的系数,根据式(6)计算得到的DUT的I-V关系如图3所示。

图3展示了DUT1、DUT2的I-V关系,包括由交流模式下的测试结果计算得到的和直流模式下直接测量到的结果。在0～80 mV区间,

电流随电压 表1 DUT的线性项和各阶非线性项系数

线性增加,当电压超过80 mV后,电流电压关系不再是线性的。在低电压区,用直流和交流模式测量得到的电流是相等的,而在高电压区则不相等。为了进一步验证交流模式的可靠性,将组成DUT的电阻换成约1 kΩ的。直流和交流模式下新DUT,即同一个二极管并联1 kΩ电阻(DUT2)的I-V关系曲线如图3中虚线所示,交流模式下计算得到的DUT2的线性项和各阶非线性项的系数见表1。很明显,低电压区(0～80 mV)用直流和交流模式测量到的I-V曲线基本相同,表明交流模式是可靠的。

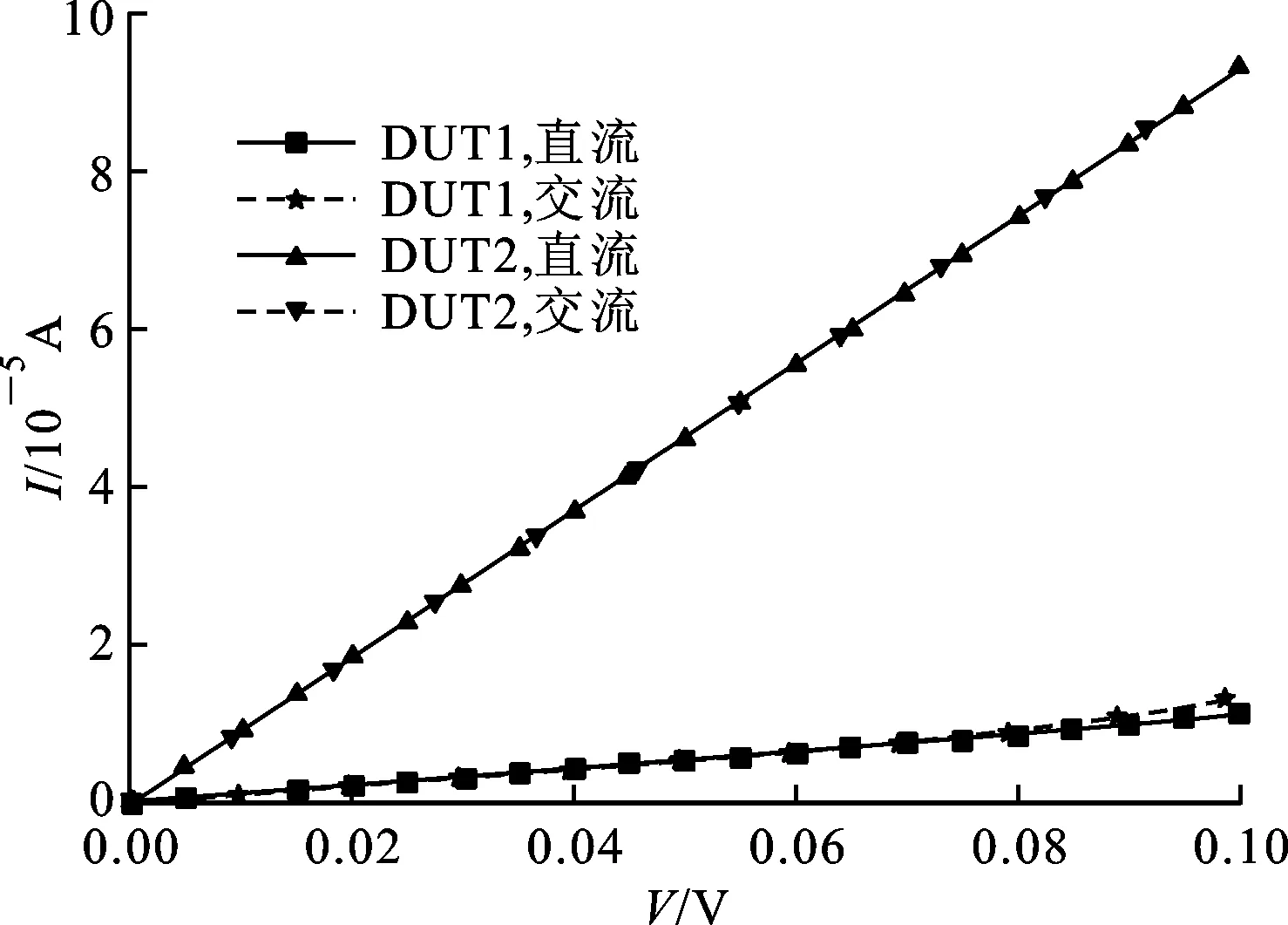
图3 DUT1和DUT2的I-V关系

在低电压区(0～80 mV),图3中的曲线表明电流和电压之间具有强的线性关系。因此,对两组DUT在直流模式下测得的I-V曲线进行了线性拟合,得到的DUT的电阻为9.49 kΩ和1.08 kΩ,相应的线性拟合系数都为0.999。由此可以得出结论:两个DUT在低电压区都是线性的。这里使用的分析I-V关系的方法被广泛使用,但是,对于分析在微波通信领域使用的部件的导电特性时,此方法并不全面,因为其无法揭示弱的非线性。受限于仪器的分辨率,直流模式主要揭示的是线性的导电特征,正如图3所示的那样。

本文中所使用的DUT由一个二极管和一个电阻组成,它们是并联关系。DUT的电阻值RD与二极管的电阻值R1以及并联电阻的阻值R2满足关系式

RD=R2/(1+R2/R1)

(7)

当R2≪R1时,RD≈R2,即DUT的电阻值近似等于并联电阻的阻值。图4所示的是二极管电阻随直流电压的变化关系。当电压由0增大到0.1 V时,二极管的电阻由2.26 MΩ减小到47.8 kΩ。在低电压区,二极管的阻值和电阻的相差非常大(即R2≪R1),因此电阻主要支配着DUT的电学特性,所以其I-V曲线是线性的,如图3中0～80 mV区间的曲线。随着电压的增大,一旦二极管的阻值接近电阻阻值时,电阻不再起主导作用,DUT的I-V曲线也不再是线性的(见图3中电压大于90 mV部分的曲线)。虽然在低电压区直流模式测得了线性的I-V关系,但是总电流中一定有来自于二极管的非线性电流的贡献,仅用直流模式进行测试和分析并不能够将其揭示出来,然而借助于交流模式,弱的非线性部分能够被分离并进行测量。

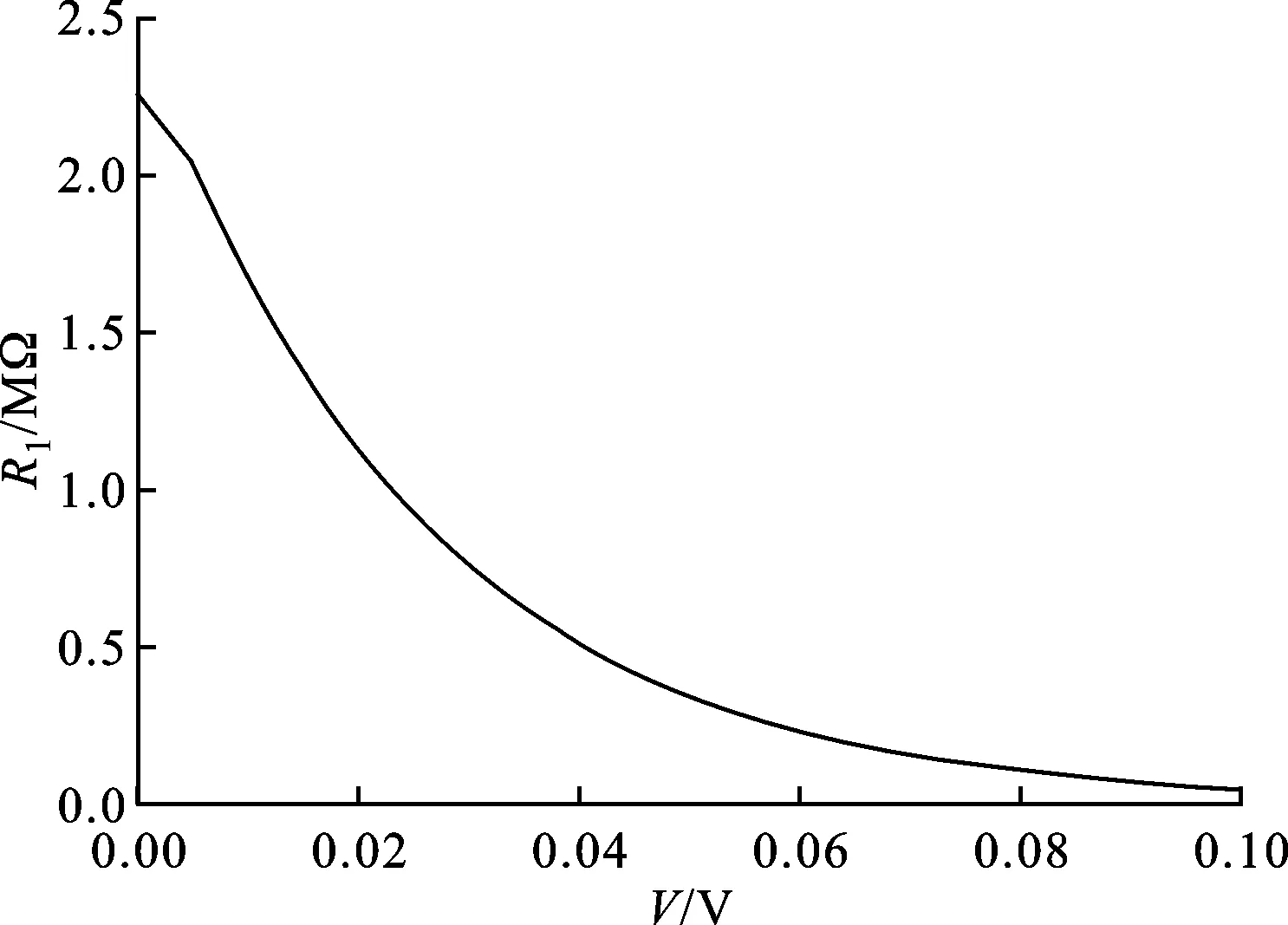
图4 二极管的电阻-电压关系

2.4 高阶谐波的I-V曲线

图5所示的是DUT1和DUT2在交流激励下各高阶谐波的I-V曲线,DUT1的谐波阶次为2到9,DUT2的谐波阶次为2到8。在计算高阶谐波的I-V曲线时,激励信号落在DUT上的有效分压由下式计算得到

VRD/(RD+R3+R4)

(8)

式中:V为激励信号振幅有效值;R3为采样电阻阻值;R4为信号源输出阻抗。

高阶谐波的电流由下式计算得到

Vn/R3

(9)

式中:Vn为第n次谐波的振幅有效值。

从图5中可以明显看出:虽然测试的DUT不同,但是来自于同一非线性源——二极管的高阶谐波所对应的I-V曲线基本相等;在低电压区(0～60 mV),由于加在DUT上的电压小,激励出的二极管的高阶谐波幅度小,因此容易受到系统噪声或信号源谐波失真影响,导致测量到的高阶谐波在此区间出现振荡;对于DUT2,测量结果显示其9次谐波在整个区间振荡,表明测量到的主要是系统噪声或信号源谐波失真,因此没有将其画出来,也无法计算其对应的非线性系数。

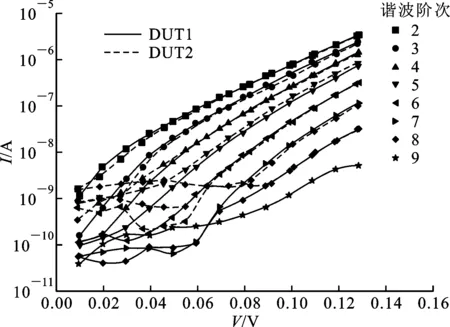
图5 DUT1和DUT2的各高阶谐波的I-V曲线

2.5 I-V曲线非线性部分

根据式(6),计算得到的DUT1和DUT2的二极管I-V关系的非线性部分如图6所示。图中电流用对数尺度显示在30～100 mV区间,两条曲线基本重合,表明虽然两个DUT是不同的,但是用交流方式得到的来自于同一二极管的I-V关系非线性部分是相同的。为了显示两个DUT的I-V关系中线性和非线性部分的差异,将直流和交流模式下得到的I-V关系曲线也一同在图6中画出。在低电压区(0～80 mV),尽管I-V关系非线性部分比线性部分要小3～4个数量级,但是交流模式能够将其分离并测量。

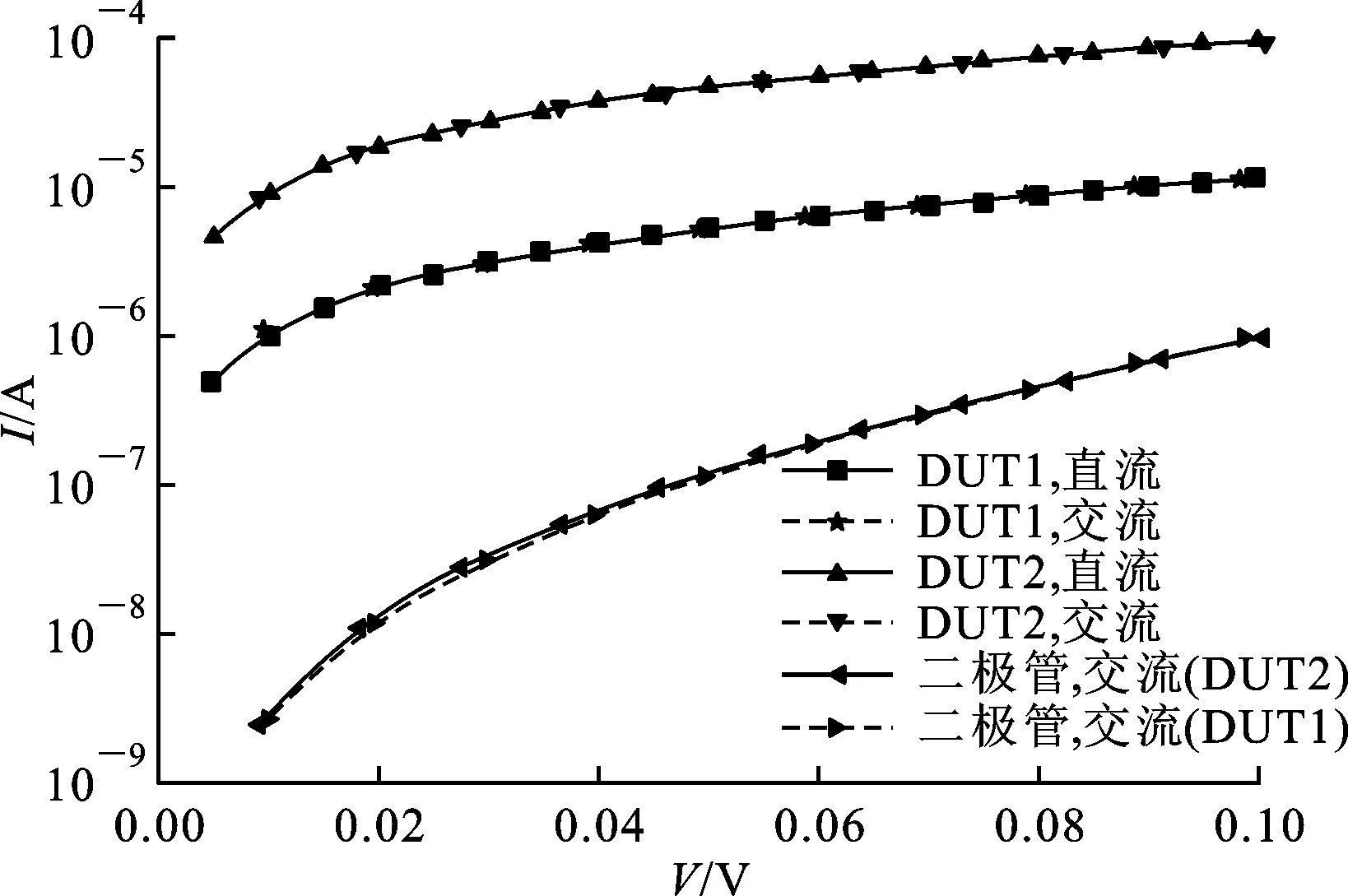
图6 DUT1和DUT2的I-V关系和二极管I-V关系的非线性部分

2.6 频率对I-V关系的影响

本文采用交流信号来激励DUT,其电容值与阻抗密切相关。由于DUT是由二极管并联电阻组成的,因此采用Agilent E4980a型LCR表,以并联模式分别测量了DUT1和DUT2在3 kHz～1 MHz频段的电容,DUT1和DUT2在此频段的并联电容值分别为7.81 pF和7.86 pF,并联电阻值分别为10 035 Ω和1 090 Ω。对于频率为878 Hz的交流信号,DUT1和DUT2的阻抗可由下式计算得到

R2/(1+(ωR2C)2)1/2

(10)

式中:ω为交流信号的角频率;C为并联电容值。

DUT1和DUT2的阻抗分别为10 035 Ω和1 090 Ω,其上的分压分别为总电压的99%和91.5%。对于PIM,一般都是在高频领域(几百MHz及以上)出现的,频率会影响趋肤深度,并可能进一步影响PIM,因此频率对非线性即PIM的影响也很受关注,而本文提出用交流激励来测量微弱的非线性,理论上可以研究频率对非线性I-V的影响,但是受限于电路的寄生参量和沿用直流的电路连接方式与相关理论,所采用的交流信号的频率有上限,不能超过1 MHz。另外,测试仪器(锁相放大器)的最高检测频率只有102 kHz,因此可选取的激励信号频率范围很有限。通过在878～11 000 Hz频率范围内进行测量,发现当电压固定时,频率越高,DUT的电流和二极管的非线性电流越小。频率对DUT的电流影响微弱,而对于二极管的非线性电流影响较大。当频率由878 Hz增大到10 787 Hz时,DUT的电流减小了约2.4%,而二极管的非线性电流减小了大约33%。图7显示了交流激励频率分别为878 Hz和10 787 Hz时,同一二极管的非线性部分的I-V曲线。

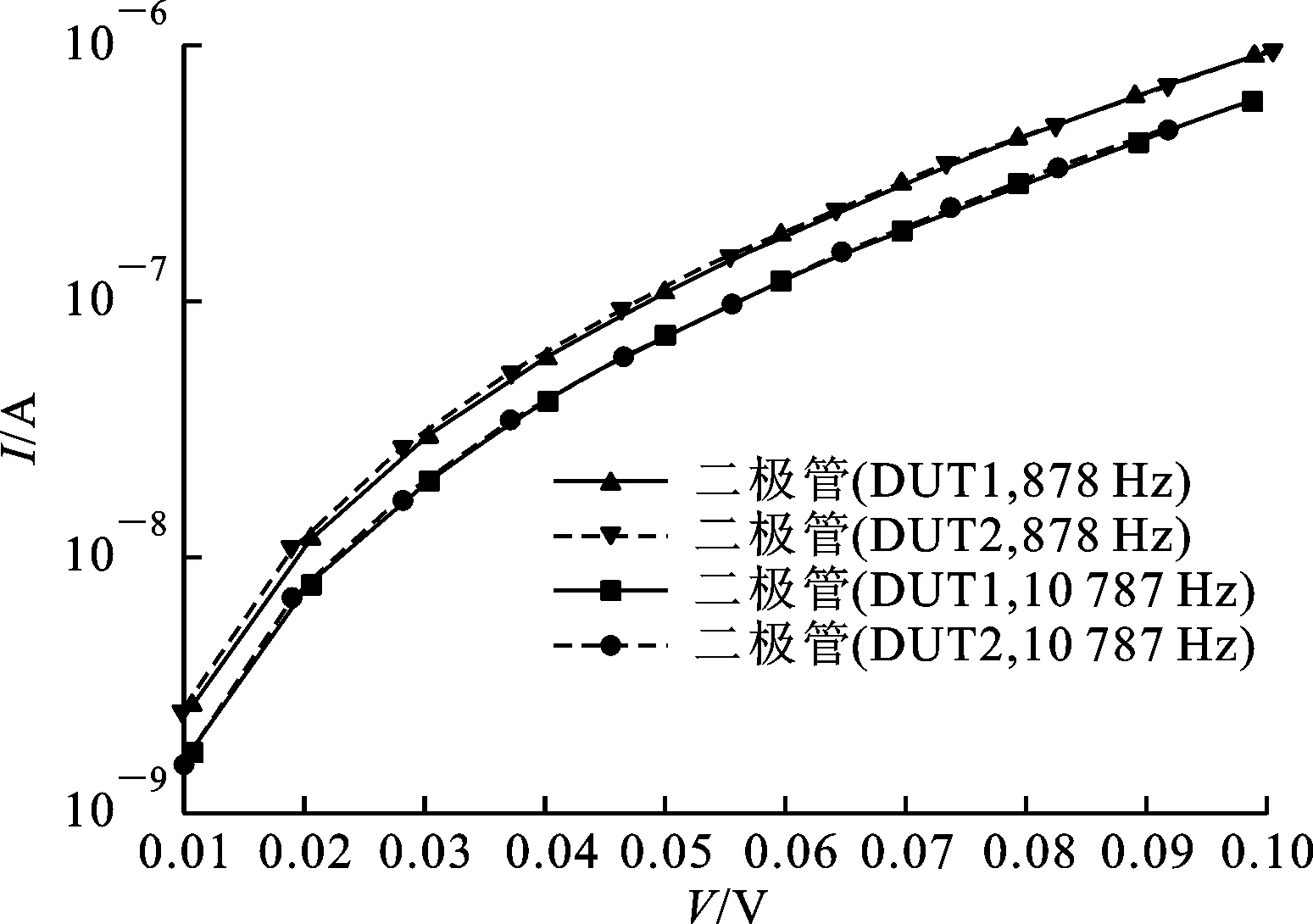
图7 不同激励频率下二极管I-V曲线非线性部分

通过上述实验结果和分析可以看出,本文提出的用交流模式来测量微弱的非线性的方法,不仅具有直流测试方法的优点(能沿用直流测试中路的相关理论),又具有射频领域测试方法的优点(线性项与非线性项在频率空间发生分离)。通过采用基于交流模式的测试方法,得到了比线性部分小3～4个数量级的I-V特性的非线性部分。这表明本文提出的交流测试方法具有可行性,能够对强线性背景中微弱非线性电流-电压的特性进行表征,可应用于部件无源互调即非线性产生机理的研究。此外,本文中所使用DUT的电流的非线性部分比线性部分低3～4个数量级,而锁相放大器的谐波失真是-80 dB,因此测量到的数据是可靠的。然而,对于实际部件,如果非线性部分比线性部分小很多,就要求交流信号源的谐波失真也要很小,这是用交流模式测量微弱非线性时需要注意的问题。

3 结 论

针对无源互调机理研究中直流模式无法在强线性背景中测量到微弱的非线性电流-电压关系这一问题,提出了基于交流模式的电流-电压测试方法,该方法能够将微弱的电流-电压非线性从强的线性背景中分离出来并进行表征。实验上选取了二极管并联一电阻为研究对象,得到了比线性背景弱3～4个数量级的电流-电压非线性部分。实验结果证实了本文方法的优越性和可行性。本文方法对于研究无源部件PIM的产生机理即非线性的机理十分有帮助。

[1] ARAZM F, BENSON F A. Nonlinearities in metal contacts at microwave frequencies [J]. IEEE Transactions on Electromagnetic Compatibility, 1980, 22(3): 142-149.

[2] PETIE J S, RAWLINS A D. The impact of passive intermodulation on specifying and characterising components [C]∥ Proceedings of the Third ESA Electronic Components Conference. Noordwijk, Netherlands: European Space Agency, 1997: 45-49.

[3] LUI P L. Passive intermodulation interference in communication systems [J]. Electronics & Communication Engineering Journal, 1990, 2(3): 109-118.

[4] 张世全, 傅德民, 葛德彪. 无源互调干扰对通信系统抗噪性能的影响 [J]. 电波科学学报, 2002, 17(2): 138-142. ZHANG Shiquan, FU Demin, GE Debiao. The effects of passive intermodulation interference on the anti-noise property of communications systems [J]. Chinese Journal of Radio Science, 2002, 17(2): 138-142.

[5] ROCAS E, COLLADO C, ORLOFF N D, et al. Passive intermodulation due to self-heating in printed transmission lines [J]. IEEE Transactions on Microwave Theory and Techniques, 2011, 59(2): 311-322.

[6] 叶鸣, 贺永宁, 王新波, 等. 金属波导连接的无源互调非线性物理机制和计算方法 [J]. 西安交通大学学报, 2011, 45(2): 82-86. YE Ming, HE Yongning, WANG Xinbo, et al. Nonlinear physical mechanism and calculation method of passive intermodulation at metal waveguide connection [J]. Journal of Xi’an Jiaotong University, 2011, 45(2): 82-86.

[7] SOMBRIN J, SOUBERCAIE-PUN G, ALBERT I. New models for passive non linearities generating intermodulation products with non-integer slopes [C]∥ 2013 7th European Conference on Antennas and Propagation. Los Alamitos, CA, USA: IEEE Computer Society, 2013: 25-28.

[8] 王斌, 陈立甲, 邱景辉. 无源互调机理模型分析及测试识别方法 [J]. 微波学报, 2014(S1): 9-14. WANG Bin, CHEN Lijia, QIU Jinghui. Mechanism model analysis and discrimination methods of passive intermodulation [J]. Journal of Microwaves, 2014(S1): 9-14.

[9] 毛煜茹, 刘莹, 谢拥军, 等. 金属接触非线性引起的无源互调效应的数值分析 [J]. 电子学报, 2015, 43(6): 1174-1178. MAO Yuru, LIU Ying, XIE Yongjun, et al. Numerical analysis of passive intermodulation due to metallic contact nonlinearity [J]. Acta Electronica Sinica, 2015, 43(6): 1174-1178.

[10]叶鸣, 吴驰, 贺永宁, 等. S波段波导同轴转换器的无源互调特性实验研究 [J]. 电波科学学报, 2015, 30(1): 183-187. YE Ming, WU Chi, HE Yongning, et al. Experimental research on passive intermodulation characteristics of S-band waveguide to coaxial adapter [J]. Chinese Journal of Radio Science, 2015, 30(1): 183-187.

[11]CHAPMAN R C, ROOTSEY J V, POLIDI I. Hidden threat-multicarrier passive component IM generation [C]∥ Proceeding of AIAA/CASI 6th Communications Satellite Systems Conference. Reston, VA, USA: American Institute of Aeronautics and Astronautics, 1976: 357-372.

[12]BOND C D, GUENZER C S, CAROSELLA C A. Intermodulation generation by electron tunneling through aluminum-oxide films [J]. Proceedings of the IEEE, 1979, 67(12): 1643-1652.

[13]HELME B G M. Interference in telecomm systems, from passive intermodulation product generation: an overview [C]∥ Proceeding of 22nd Antenna Measurement Techniques Association Annual Meeting and Symposium. Atlanta, GA, USA: Antenna Measurement Techniques Association, 2000: 143-149.

[14]HIGA W H. Spurious signals generated by electron tunneling on large reflector antennas [J]. Proceedings of the IEEE, 1975, 63(2): 306-319.

[15]叶鸣, 贺永宁, 崔万照. 基于电热耦合效应的微带线无源互调机理研究 [J]. 电波科学学报, 2013, 28(2): 1-6. YE Ming, HE Yongning, CUI Wanzhao. Passive intermodulation mechanism of microstrip lines based on the electro-thermal coupling effect [J]. Chinese Journal of Radio Science, 2013, 28(2): 1-6.

[16]WILLEMSEN B A, KIHLSTROM K E, DAHM T. Unusual power dependence of two-tone intermodulation in high-Tc superconducting microwave resonator [J]. Applied Physics Letters, 1999, 74(5): 753-755.

[17]KOZYREV A B, SAMOILOVA T B, GOLOVKOV A A, et al. Nonlinear behavior of thin film SrTiO3capacitors at microwave frequencies [J]. Journal of Applied Physics, 1998, 84(6): 3326-3332.

[本刊相关文献链接]

徐田华,杨连报,胡红利,等.高速铁路信号系统异构数据融合和智能维护决策.2015,49(1):72-78.[doi:10.7652/xjtuxb201501012]

惠萌,刘盼芝,白璘,等.非自治铁磁谐振电路过电压脉冲时滞同步抑制方法研究.2014,48(6):55-59.[doi:10.7652/xjtuxb201406010]

韦兆碧,杨银堂,马志瀛,等.聚磁式光学电流互感器饱和特征的记忆效应补偿研究.2013,47(6):97-102.[doi:10.7652/xjtuxb201306017]

庞霞,刘凌,刘崇新,等.利用异结构同步对铁磁混沌电路的非线性反馈控制.2015,49(4):18-23.[doi:10.7652/xjtuxb 201504004]

张瑶,张鸿,李梁,等.时钟数据恢复电路中的线性相位插值器.2016,50(2):48-54.[doi:10.7652/xjtuxb201602009]

宋国兵,常仲学,王晨清,等.直驱风机三相短路电流特性分析.2015,49(10):1-7.[doi:10.7652/xjtuxb201510001]

王小鑫,闫洁冰,胡红利,等.利用正交试验的电容传感器仿真及优化设计.2013,47(2):81-86.[doi:10.7652/xjtuxb 201302014]

姚学玲,杜志航,杨志豪,等.气体放电管直流击穿电压测量技术的研究.2012,46(10):1-7.[doi:10.7652/xjtuxb201210 001]

(编辑 刘杨)

Measuring Method of Weak Nonlinear Current-Voltage Relationship Based on AC Excitation

HE Yun1,2,BAI Chunjiang1,WANG Xinbo1,BAI He1,HU Tiancun1,CUI Wanzhao1,LIU Chunliang2

(1. National Key Laboratory of Science and Technology on Space Microwave, China Academy of Space Technology (Xi’an),Xi’an 710100, China; 2. School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A new method based on AC excitation is proposed to characterize the weak nonlinear current-voltage relationship in huge linear background, which is hardly measured by the DC method in the study of passive intermodulation mechanism of RF and microwave components. The current-voltage relationship of the nonlinear system is firstly analyzed when AC voltage is applied and its expression is derived, then samples consisting of a diode in parallel with different resistors are measured The coefficients for linear and nonlinear parts are calculated from the measured amplitude of harmonics with different order, the current-voltage relationship of samples and the weak nonlinear part of the current-voltage relationship coming from diode are also obtained from the resulting expression. Results show that the proposed method obtains a weak nonlinear part of current which is 3-4 orders smaller than the linear part in magnitude, and exhibits advantage of the method over traditional DC method. Moreover, the calculated weak nonlinear parts of currents coming from the same diode with different samples are almost equal, and the practicability of the method is confirmed. The method will offer a new way for investigating nonlinear conduction mechanism that is resulted in passive intermodulation.

passive intermodulation; nonlinearity; current-voltage; harmonics

2015-11-24。 作者简介:何鋆(1987—),男,博士后;崔万照(通信作者),男,博士,研究员。 基金项目:国家自然科学基金资助项目(1537211,61574113);空间微波技术重点实验室基金资助项目(9140C530101130C53013);中国博士后科学基金资助项目(2015M572661XB)。

时间:2016-04-03

10.7652/xjtuxb201606015

TM930.1

A

0253-987X(2016)06-0097-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160403.1846.012.html