含风电系统大规模长时间机组组合分解模型
2016-12-23宫本辉王秀丽党灿姚力侯孚睿
宫本辉,王秀丽,党灿,姚力,侯孚睿
(西安交通大学电气工程学院,710049,西安)
含风电系统大规模长时间机组组合分解模型
宫本辉,王秀丽,党灿,姚力,侯孚睿
(西安交通大学电气工程学院,710049,西安)
针对传统机组组合忽略模型优化、仅从优化数学求解算法的角度加快求解速度的问题,提出了基于数学优化和模型优化的机组组合分解模型,以加快含风电的机组组合的求解速度,并采用弃风密度曲线来评估系统的弃风状况。该模型通过将传统机组组合求解空间分解为由离散变量决定的离散空间,结合机组组合问题的实际物理特点,剔除不具有实际意义的求解区域,以加快求解速度。弃风密度曲线可以通过系统弃风率范围及各弃风率的密度概率更好地评估系统弃风状况。根据所提方法和某省电网实际算例,比较了所提模型与传统模型的计算速度,并运用弃风密度曲线评估算例的弃风状况。研究结果表明,相比于传统的机组组合模型和弃风期望值,机组组合分解模型明显加快求解速度,系统的弃风状况在弃风密度曲线上从曲线中心向两侧波动展开,该研究加快了含风电系统的机组组合求解速度以及对系统风电弃风状况的评估更加有效、合理。
风电;机组组合分解模型;机组组合;弃风密度曲线;生产模拟
随着新能源的大规模并网及全球能源互联网建设的不断推进,电力系统对能源结构的配置水平不断提高。机组组合问题在优化资源配置、优化能源结构及促进系统安全经济运行方面起到了重要作用。然而,机组组合使混合整数规划问题的求解难度随着系统规模与求解时间长度的增加而迅速增大,因此针对大规模系统长时间机组组合问题进行快速求解成为学术界与工业界的研究热点。
为求解机组组合问题,国内外学者从20世纪70年代就开展了大量富有成效的工作。目前,机组组合问题的近似求解算法得到很大的发展,主要方法有人工智能算法和优化算法两大类。人工智能算法主要包括进化算法[1]、遗传算法[2-3]、蚁群算法[4]、神经网络算法[5]和模拟退火算法[6]等,这些算法加快了大规模长时间的机组组合问题的求解速度,但无法保证所求解的最优性。优化算法通过优化求解空间的边界约束,寻找最优解。文献[7]将优化过程分为前推和回代的过程,逐渐缩小求解空间,最终寻得最优解;文献[8]将大规模的问题分解为很多小问题,通过不断求解小问题来求得最优解;文献[9-10]通过不断填加Benders割集约束与非可行域约束,缩小求解空间,最终求得最优解;文献[11]通过先将求解空间转变为一个高维求解空间,然后将此空间向低维空间映射,缩小求解空间,达到加快求解速度目的。Benders分解和Lift-and-Project算法在计算中小规模的机组组合问题时可以取得非常好的效果,然而求解大规模长时间机组组合时的计算速度较慢。
目前的研究中多将机组组合问题看成是一个数学优化问题,采用数学优化求解方法对其求解,鲜见文献根据实际问题的特点,通过对模型进行优化,结合数学优化算法达到加快求解速度的目的。从欧式空间几何的角度,机组组合问题中大量0-1变量使机组组合的解空间在欧式空间中不连续,且互不连续的解空间存在有不同时发生的互斥关系,即在实际电力系统运行中两种不同的机组运行方式不可能同时发生。机组组合问题中的0-1变量代表的是电力系统中发电机组的开、停机情况,大量的0-1变量组成了复杂的离散求解空间。然而,在实际电力系统运行过程中,最优解只会集中在由几种组合组成的求解空间内,大量的0-1组合的求解空间是不存在最优解的。
基于上述思路,本文在Benders分解和Lift-and-Project算法思路的基础上,提出基于物理意义和数学优化的机组组合分解模型(DUCM),由机组组合第1分解模型(DUCM-Ⅰ)和机组组合第2分解模型(DUCM-Ⅱ)组成。DUCM-Ⅰ模型是根据实际系统的机组及负荷特性,在保证系统可靠性及最大程度接纳风电的同时来确定系统机组的基本运行方式,剔除不可能存在的运行方式,这相当于在求解空间上剔除了不可能存在0-1变量组合的解空间,确定了几种符合实际电力系统运行特点的0-1组合方案。DUCM-Ⅱ模型在DUCM-Ⅰ的基础上,当0-1变量全部或绝大多数被确定后,采用CPLEX优化软件对连续或只含有少量0-1变量的DUCM-Ⅱ模型进行求解。利用简单数学系统和我国东北某省电网实际算例对所提算法思路进行诠释,并用弃风密度曲线综合评估的弃风状态,验证了所提方法的快速性和有效性。
1 机组组合分解模型
1.1 含风电场机组组合问题
含风电场的长时间多区域机组组合模型的目标就是系统运行成本最小
Us,iatpIs,iatp+Ds,iatpIs,iatp]
(1)
式中:Np为计算时间内的周期数;Nt表示模拟电网的运行时间;Na为计算区域的分区数量;Ng为计算区域常规机组数量;CF,iatp(Piatp)为机组燃料成本函数,采用二次函数关系进行计算;Piatp为区域a、机组i在周期p、时间t时的出力;Us,iatp和Ds,iatp分别表示区域a、机组i在周期p、时间t时的启动和关闭费用。
发电约束包括功率平衡约束和系统的备用约束,表达式如下
∀a∈[1,Na], ∀t∈[1,Nt], ∀p∈[1,Np]
(2)
(3)
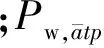
备用容量可以分为向上热备用容量和向下热备用容量,通常所说的热备用就是指向上备用容量。向上备用容量容量和向下备用容量是一对矛盾:向上备用容量大,增强系统可靠性,火电机组开机数量增多,压缩向下备用容量,造成系统弃风及火电机组年利用小时数降低;向下备用容量增大,即系统的热备用不足,虽然增大了系统的风电接纳率,却使系统的可靠性降低。结合我国目前在电网运行中保证电网可靠性运行的同时,最大程度接纳风电上网的政策,在确定火电机组的开机方式后,应该首先安排火电机组按照最小技术出力(供热期为最小热出力)运行,然后接纳风电出力,最后再安排热备用承担负荷,具体安排火电机组的开机方式受到下式约束
(4)
式中:Pia,max表示区域a、机组i的最大出力。
火电机组的向上和向下爬坡率可以表示为
Piatp-Pia(t-1)p≤[1-Iiatp(1-Iia(t-1)p)]Ru,i+
Iiatp(1-Iia(t-1)p)Pi,min
Pia(t-1)p-Piatp≤[1-Iia(t-1)p(1-Iiatp)]Rd,i+
Iia(t-1)p(1-Iiatp)Pi,min
(5)
式中:Ru,i和Rd,i为机组i向上爬坡速度和向下爬坡速度;Pi,min为机组i的最小技术出力;Iiatp是整数变量,为区域a、机组i在周期p、时间t时的启停情况,取1时表示机组开启,取0时表示机组关闭。
火电机组的最小开、停机时间为
(6)
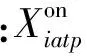
火电机组的出力限制如下
Pi,minIiatp≤Piatp≤Pi,maxIiatp
(7)
式中:Pi,min为机组i的最小技术出力。
风电在周期p、时间t时最大预测出力为Pw,max,tp,此时风电出力Pw,atp的约束如下
0≤Pw,atp≤Pw,max,atp
(8)
从全国范围看,弃风主要原因除了调峰容量不足、风电出力与负荷不平衡外,还有输送通道约束。风电出力输出方式如图1所示,风电出力经35 kV变电站汇集到220 kV或330 kV线路,在经过本地消纳后,最终剩余风电出力与火电机组出力通过500 kV或者750 kV线路输出。在实际电网调度运行中,由于输电通道约束造成的弃风主要发生在图1中的L1及L2输电线路上[12],在含风电的多区域机组组合模型中,考虑输送通道约束进行分区,对输送通道进行约束如下
Pl,t,min≤Pl,t≤Pl,t,max
(9)
(10)
式中:Pl,t为输电线路l在t时刻的输送功率;Pl,t,max为最大功率;Pl,t,min为最小功率;∑Pthermal,t,base为各区域火电机组最小出力在平衡本区域负荷后,通过联络线向其他区域的功率;∑Pthermal,t,reserve为各区域在安排完火电后,火电机组增量出力通过联络线向相邻区域提供的功率。
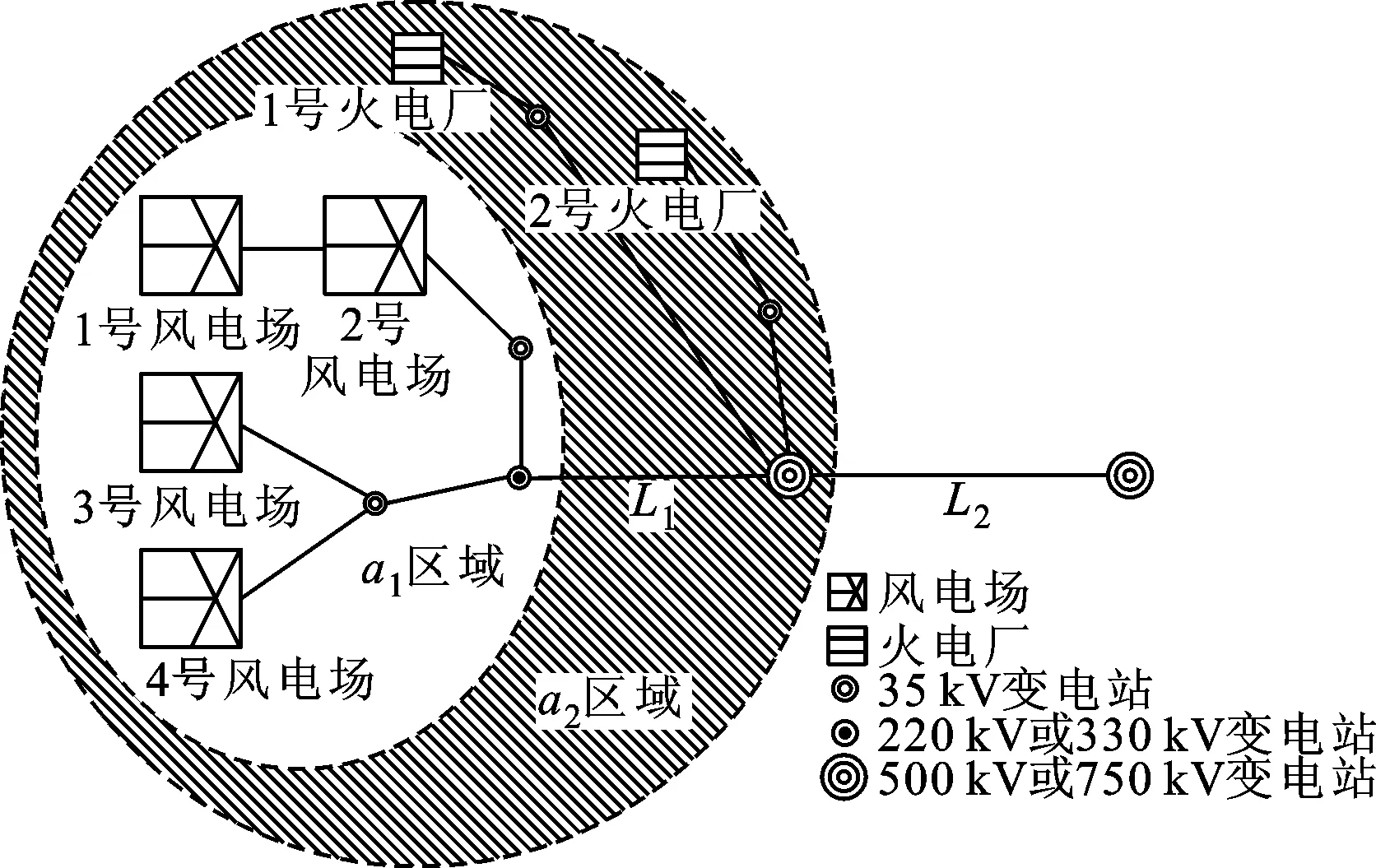
图1 风电区域功率外送示意图
通过式(2)、式(8)~式(10)可知,区域a、时间t的风电预测出力在平衡区域a负荷后,通过联络线向其他区域输送功率,同时本区域的负荷也接收非本区域的风电出力,这样不同时空的风电出力可以很好地互补,提高风电的接纳率。
为了便于表述,将式(2)~式(6)分别用下式表示
CII+CPP≤cuc
(11)
DII+DPP+DSS≤duc
(12)
式中:I=(Ii),Ii=(Ii,t);P=(Pi),Pi=(Pi,t);S=(Si),Si=(Si,t);CI和CP为式(2)和式(3)的系数矩阵;DI、DP和DS分别为式(5)和式(6)的系数矩阵;cuc和duc为对应的常量向量。综合式(1)~式(12),得到含风电的机组组合模型
Us,iatpIs,iatp+Ds,iatpIs,iatp]

(13)
1.2 机组组合问题的分解模型的建立
文献[13]采用软件GAMS调用CPLEX优化求解器求解混合整数规划,大大加快了求解速度。然而,CPLEX优化软件的特点就是随着模型阶数、时间长度的增加,求解速度大幅下降。当用文献[13]方法对式(13)进行求解时,CPLEX求解器会因为求解模型空间复杂而增加求解时间。因此,如何根据式(13)大规模、长时间的特点,将模型的可行域空间变小,成为模型加快计算速度的关键。
文献[14]研究表明,风电场群出力变化率每分钟装机容量在0%~1.5%之间的概率为99%,火电机组的出力调整速率为每分钟额定容量的3%~5%,因此火电机组的调整速率可以跟上风电的波动速率。同时,根据实际电力系统调度运行特点及电气设备的经济运行和寿命安全要求,火电机组的启停是每一个周期调整一次,而非每时每刻都调整,因此将火电机组的最小开停机时间约束忽略,式(13)变为机组组合简化模型(SUCM)如下
Us,iatpIs,iatp+Ds,iatpIs,iatp]
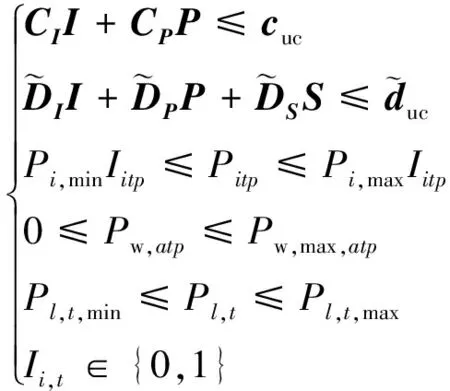
(14)
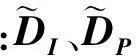
SUCM模型的特点是整数变量和连续变量同时存在且其构成的可行解空间在欧式空间中相互交叉,这就增大了优化搜索空间,由于搜索空间是不连续的,其求解速度将大幅下降。因此,将SUCM中的整数变量和连续变量分离,缩小优化搜索空间,将加快求解速度。
为将机组组合模型中的整数变量和连续变量分离,对发电机输出功率Pi,t进行离散-连续变换
(15)
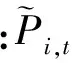
(16)
火电机组燃料费用计算方式如下
CF(Pi,t)=ai,t+bi,tPi,t+ci,t(Pi,t)2
(17)
根据式(15)~式(17),可以得到变换后的火电机组燃料费用
(18)
由式(1)~式(5)和式(15),得到
Piatp,min)+IiatpPiatp,min]+Us,iatpIs,iatp+Ds,iatpIs,iatp}
(19)
∀a,∀t,∀p
(20)
(21)
(22)
于是,SUCM模型中的约束在经过式(15)变换后,得到的机组组合分解模型(DUCM)如下
Piatp,min)+IiatpPiatp,min)+Us,iatpIs,iatp+Ds,iatpIs,iatp]

(23)
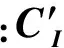
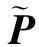
在实际的电力系统运行中,开机方式在调整周期T内的负荷曲线存在最大值与最小值。在每一调整周期内的所有火电开机的最大出力需要不小于系统最大负荷及备用需求,最小出力需要不大于系统最小负荷。同时,为满足最大接纳风电,需要在满足上述条件的前提下保持开机容量最小,可通过式(24)确定调整周期T内的火电机组开机方式
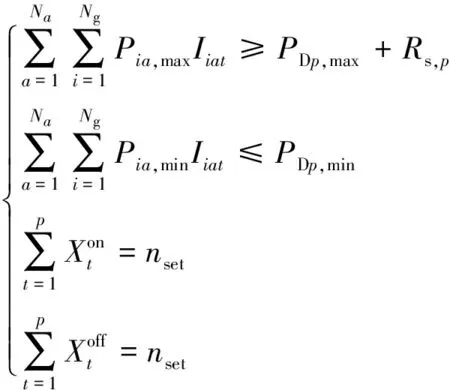
(24)
式中:nset为周期内机组调度调整次数;Iiat∈{0,1}。
Piatp,min)]+CF,iatp(IiatpPiatp,min)+
Us,iatpIs,iatp+Ds,iatpIs,iatp}
(25)
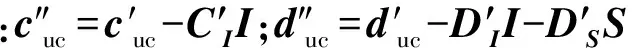
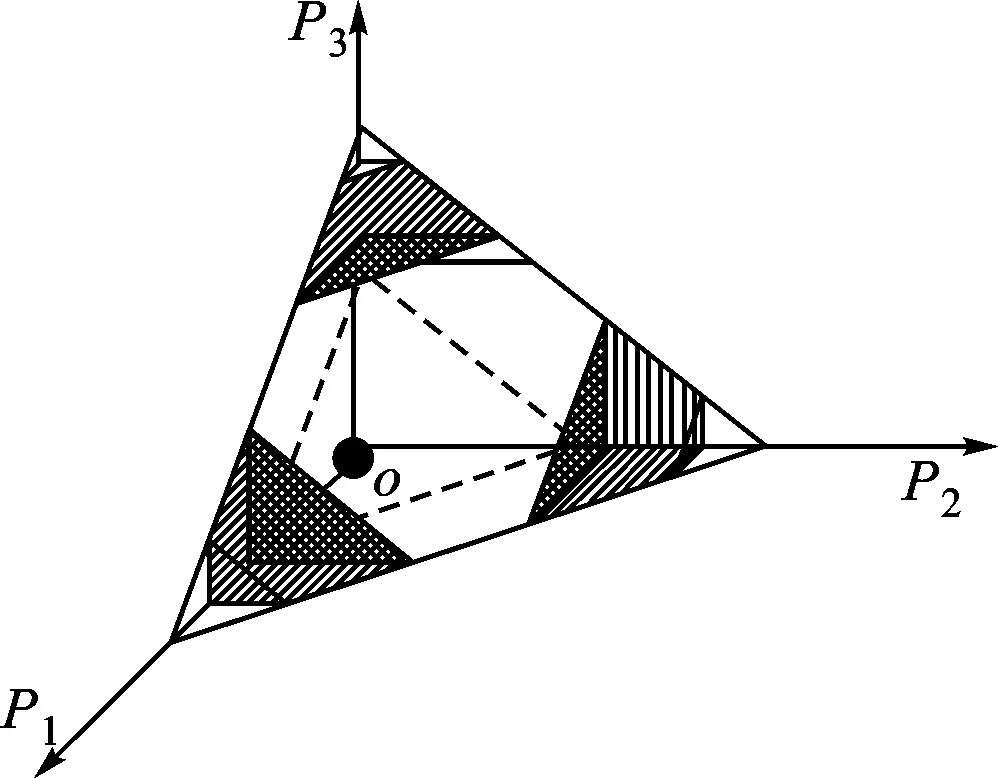
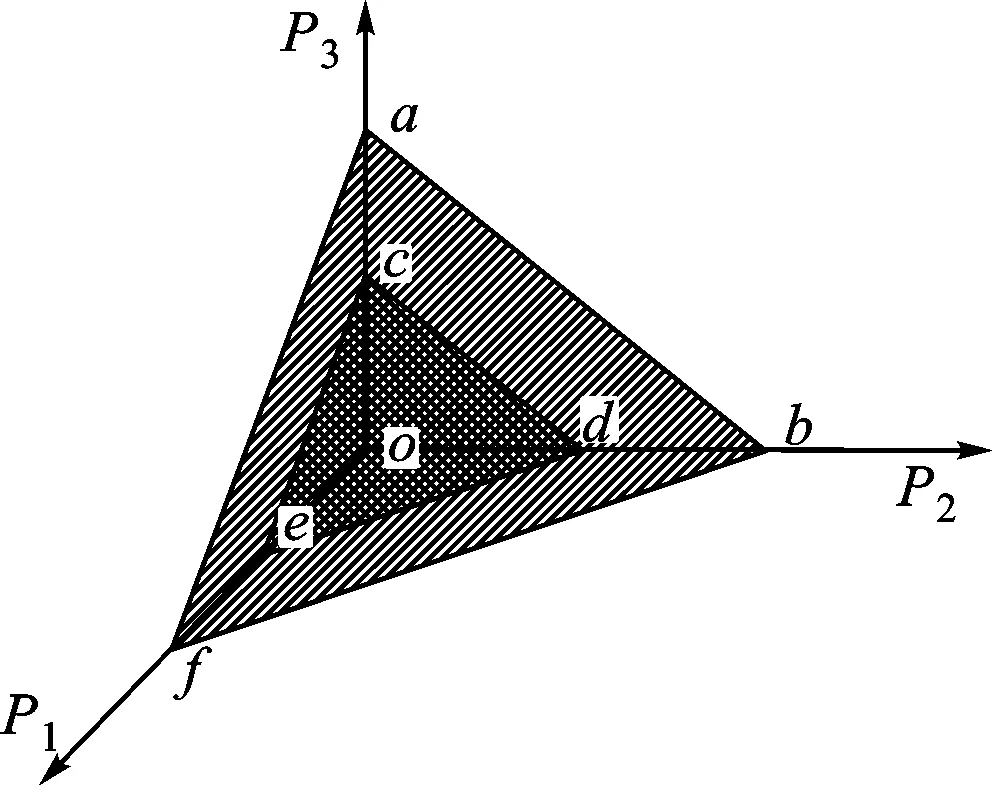
需要指出的是,式(24)为模型DUCM-Ⅰ,式(25)为模型DUCM-Ⅱ,二者共同组成了模型DUCM。模型DUCM-Ⅰ是在保证系统可靠性及机组周期内最小开停机次数约束条件下,确定周期内火电机组开机方式,模型DUCM-Ⅱ是根据模型DUCM-Ⅰ确定开机方式后确定各机组的出力情况,此时模型DUCM-Ⅱ为连续变量模型。如果根据模型DUCM-Ⅰ确定的开机方式,在模型DUCM-Ⅱ计算的结果不满足系统的安全约束时,就需要模型DUCM-Ⅰ调整开机方式,其迭代关系如图2所示。
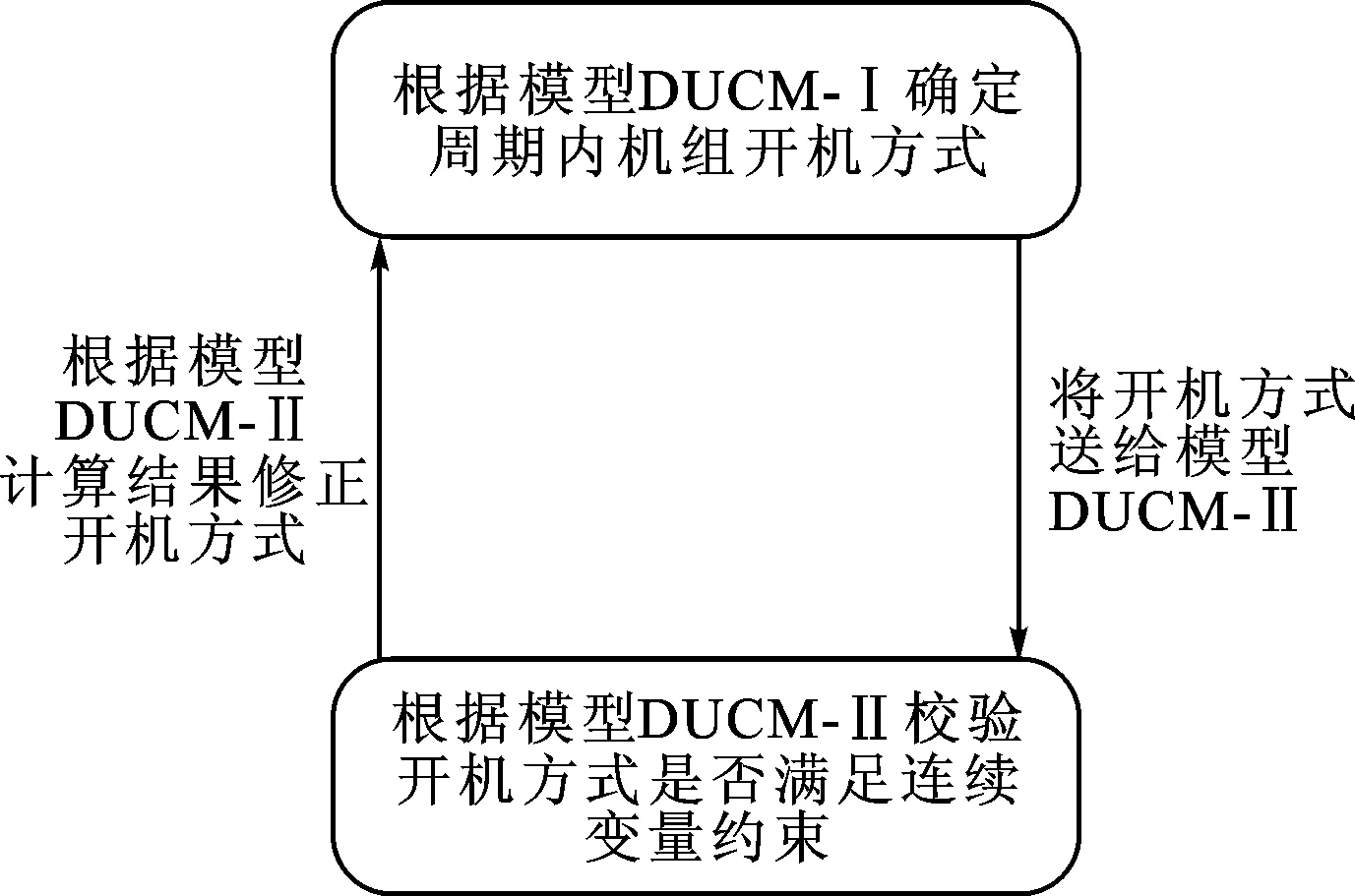
图2 模型DUCM-Ⅰ与模型DUCM-Ⅱ的关系
2 弃风密度曲线
从全国范围来看,弃风主要有3大原因:调峰容量不足,风电出力与负荷需求之间不匹配,风电输出通道受限。弃风密度曲线反映的是综合考虑风电出力与系统负荷的时序特性、系统调峰容量及风电输出通道约束的弃风情况。
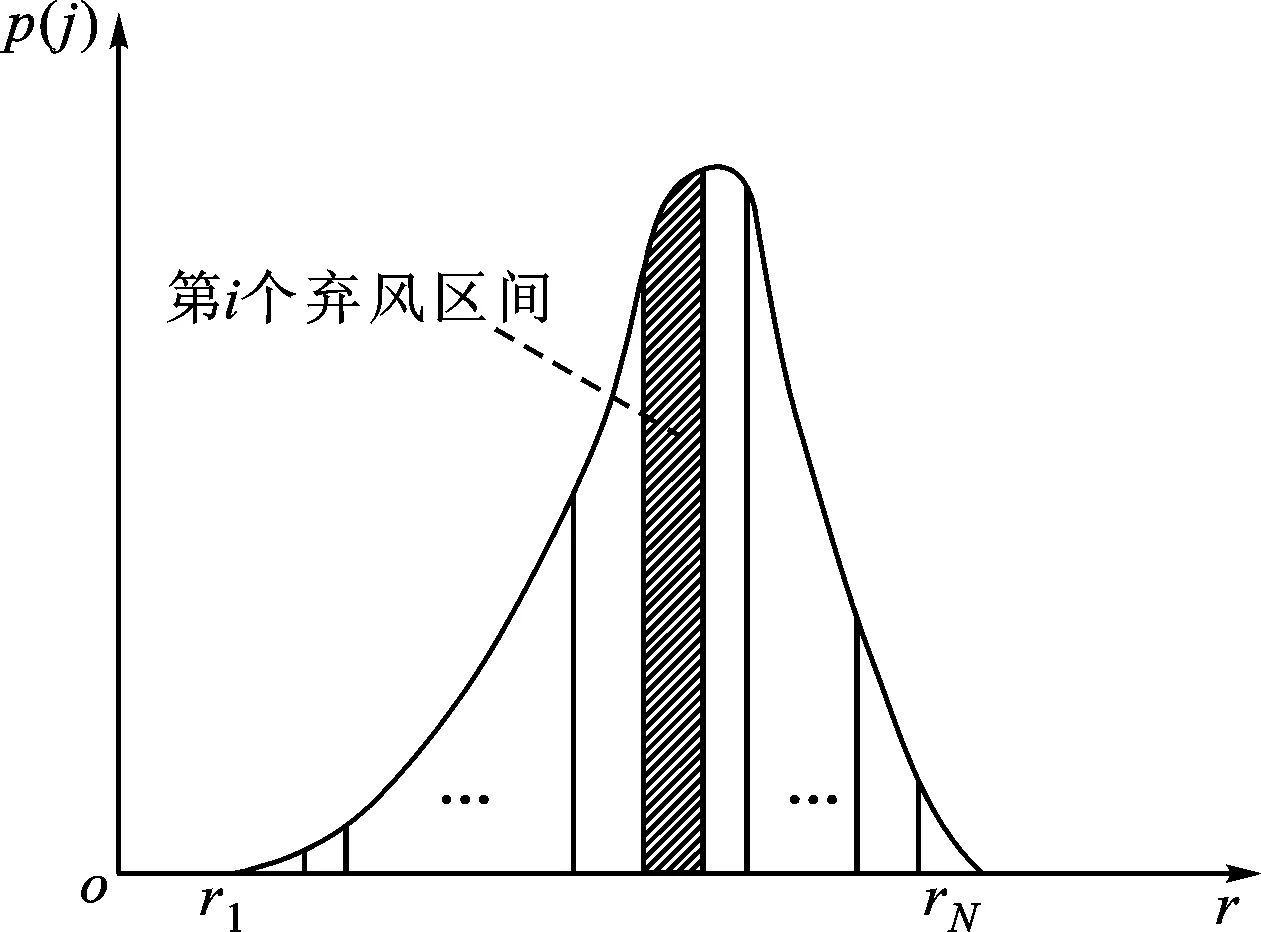
图3 弃风密度曲线示意图
风电出力具有随机性与不确定性,文献[15]指出,风电出力曲线可以分解为大波动、中波动、小波动和随机波动。采用文献[15]算法,预测该地区考虑随机性的风电出力曲线,根据模型DUCM对每一条预测风电出力曲线进行计算,得到同时考虑3大弃风原因的系统弃风率,对弃风率从小到大排序得到集合R={i|ri},i=1,2,3,…,N;其中N表示预测得到的风电出力曲线的条数,r1 (26) 式中:nk是判断第k个弃风率是否属于第j个弃风密度区间的整数变量。当第k个弃风率属于第j个弃风密度区间时nj=1,反之nk=0。 含风电多区域机组组合分解模型的计算方法及运用密度曲线评估系统弃风状况的具体步骤如下: (1)预测N条风电出力曲线,对风电曲线序列n置初值; (2)在风电序列确定后,初始化系统参数p=1; (3)根据系统中火电机组及负荷情况,形成机组组合模型,将机组组合模型分解成模型DUCM-Ⅰ和DUCM-Ⅱ; (4)求解模型DUCM-Ⅰ,得到火电机组的初步开机方式,然后转步骤(5)中的模型DUCM-Ⅱ; (5)根据步骤(4)确定的机组开机方式,求解模型DUCM-Ⅱ,如果开机方式满足约束要求转到步骤(6),如果开机方式不满足约束要求则返回步骤(4),调整开机方式; (6)判断系统的正旋转备用是否满足风电要求,若满足就将机组出力的最小值从负荷中减去,然后按照时序计算的方法安排每一时刻风电的上网电量,到步骤(7),如不满足系统要求,则返回步骤(4)调整机组的开机方式; (7)记录周期p的开机方式及机组出力,令p=p+1,返回步骤(2); (8)计算并保存期望弃风率,若n 4.1 简单数学系统 首先用一个简单的数学系统对所提模型DUCM加快计算速度的原理进行分析。文献[16]提出机组组合的爬坡约束在大部分系统中为非有效约束,不会影响模型求解空间,这里为说明方便,不考虑系统中机组的爬坡约束,只根据功率平衡约束和机组出力约束构造简单的数学系统,其模型如下 (27) 式中:I1、I2和I3表示是整数0-1变量;P1、P2和P3表示连续变量。I1、I2和I3的取值会影响P1、P2和P3的值。 机组组合分解模型能够提高计算速度最主要的原因是,该模型根据所描述物理问题的特点缩小求解空间,将最终的求解空间变成连续的。取模型SUCM的求解空间为Ω、模型DUCM的求解空间为Ω′。从图4可知,Ω的求解空间共分为8部分,分别是图4a的原点和3个小阴影空间体,图4b的3个阴影面abde、acfe和bdfe以及图4c的阴影体cde-abf。根据式(24),得到式(27)的模型DUCM-Ⅰ如下 (28) (a)I1、I2、I3中最多一个取1 (c)I1、I2、I3中全为1图4 模型DUCM的求解空间Ω 根据式(28)可以得到I1、I2和I3都为1,对应的求解空间如图4c所示。相比于模型SUCM需要在8部分离散空间中求解,模型DUCM的求解空间Ω′只是在图4c中求解,且模型DUCM的求解空间是连续的。对于凸集合的凸规划问题,解一定在可行求解空间的表面,考虑到大规模系统长时间机组组合是高阶的问题,采用模型DUCM能够将求解空间缩小到很小的空间表面,即Ω′≪Ω,这会加快求解速度,缩短计算时间。 4.2 实际系统算例 本文采用我国东北某省电网实际系统作为算例,该系统火电机组为54台,火电装机总容量为13 090 MW,其中凝汽式机组装机容量为3 060 MW,抽气式机组装机容量为10 030 MW;负荷最大为9 425.46 MW;风电装机总容量为4 278 MW。根据系统电源输送通道约束,将系统分为3个区,区域子系统装机容量关系如图5所示。算例以7 d为一个计算周期,全年52个周期的最大负荷与最小负荷值如图6所示。 图5 各子区域电网各类型电源装机比例 图6 该省一年52个计算周期的最大负荷与最小负荷 4.2.1 模型计算速度与精度 本文将对以下两个模型进行求解,以验证机组组合分解模型在求解上的优越性。 模型1:东北某省含风电考虑联络线约束实际系统的机组组合模型; 模型2:在模型1基础上对该省系统的机组组合模型进行分解,建立本文所提机组组合分解模型。 采用C++调用商业优化软件CPLEX分别对模型1和模型2进行求解,运用两种模型对1~25周内不同运行时间进行计算并对比,结果如图7所示。从图7可知,在不同求解时间长度上,模型2的求解速度都明显快于模型1,随着电网运行时间的增加,模型1与模型2之间的仿真时间相差越来越大。这种差别的原因是:模型2的机组组合分解模型根据问题的实际特点,采用切割解空间的思路,剔除不存在可行解的求解空间,减少了约束变量。以电网运行1周为例,模型1的变量数目为9 576个,采用模型2时,变量总数目仅为1 398个。对比两个模型,模型2的求解变量数目减少,求解空间变小,且由于模型2的离散变量数目在模型DUCM-Ⅰ中基本确定,模型2的连续性要优于模型1,因此模型2的求解速度明显快于模型1。 图7 两种模型仿真时间的比较 图8 年度弃风密度曲线 4.2.2 运用模型2对系统进行分析 为描述系统受风电出力的随机性、系统调峰容量、系统负荷与风电出力不平衡、风电输送通道同时影响下的弃风状况,运用所提机组组合分解模型对系统弃风进行评估,得到系统全年的弃风密度曲线如图8所示。从图8可知,系统弃风密度曲线以34.3%为中心向两侧展开,与预测风速呈正太分布或者具有厚尾效应的t分布不同,系统弃风密度曲线在向两侧展开的过程中存在波动现象,这是由于系统弃风受到风电时空特性及输送通道限制的影响。相比于通过研究风速概率特征而得到反映风电弃风期望值的方法,弃风密度曲线能够在考虑风电的时空特性、系统的调峰容量及风电输送通道的前提下更好地描述风电的弃风状况。 从实际系统算例中选取供热期和非供热期典型周,运用本文模型进行分析,其结果如图9所示。从图9可知,在供热季只接纳很少的风电,在非供热期风电几乎全部接纳。这主要是由于:在供热期要开启大量的供热机组,火电机组的最小出力大量挤压了风电的接纳空间,造成系统大量弃风;然而,在非供热季由于系统不存在供热任务,系统在保证系统可靠性前提下开启的火电机组较少,系统有足够的接纳风电的空间,系统弃风现象不是很严重。从图10可知,系统弃风主要发生在供热任务较重的1、2、3、11、12月,在不具有供热任务或者供热任务不重的4~10月几乎不存在弃风现象。 (a)供热期 (b)非供热期图9 供热期与非供热期典型周各类型电源承担负荷情况 图10 一年中各月份风电接纳情况 从实际系统算例中选取供热期典型日及非供热期典型日进行分析,得到供热期典型日与非供热期典型日全天弃风状况如图11所示。从图11可知,由于在供热期开启供热机组较多,火电机组的最小出力较大,即使风电和正旋转备用出力不参与负荷平衡,火电机组的最小出力仍大于负荷,这时就需要引入虚拟负荷或者减少供热,维持系统安全稳定运行。通过比较供热期典型日与非供热期典型日风电接纳情况,该省电网弃风现象主要发生在22时到次日7时。这段时间风电出力高而负荷较低,由供热机组的特性,系统在此时没有负荷空间接纳风电。通过算例分析,该省系统的弃风主要发生在供热期,且多发生在供热期的夜间。 (a)非供热期 (b)供热期图11 供热期与非供热期典型日机组组合出力情况 本文引入了机组组合分解模型和弃风密度曲线,对传统机组组合模型进行离散-连续变换,得到不含或仅含少量整数变量的机组组合分解模型,通过对机组组合分解模型计算得到的多个期望弃风率的分析,构建弃风密度曲线。通过对实际系统算例分析可以得出以下结论。 (1)本文所提模型与传统模型相比,可以明显缩小求解空间,减小约束变量,加快求解速度。 (2)由于系统弃风主要受调峰容量不足、风电出力与负荷需求不匹配和风电输出通道的约束,相比于系统期望弃风值,弃风密度曲线能够更好地评估系统的弃风情况。 需要指出的是,本文方法可以快速对弃风特性进行评估,为系统调度运行及在电力市场环境下需求侧响应的相关政策的制定提供依据。 [1] TRIVEDI A, SRINIVASAN D, PAL K, et al. Enhanced multiobjective evolutionary algorithm based on decomposition for solving the unit commitment problem [J]. IEEE Transactions on Industrial Informatics, 2014, 11(6): 1346-1357. [2] TRIVEDI A, SRINIVASAN D, REINDL T, et al. A multi-objective genetic algorithm for unit commitment with significant wind penetration [C]∥2015 IEEE Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 2015: 311-318. [3] BORIS P L, JESSICA S C. A deterministic annular crossover genetic algorithm optimization for unit commitment problem [J]. Expert Syst Appl, 2011, 38: 6523-6529. [4] 陈烨, 赵国波, 刘俊勇, 等. 用于机组组合优化的蚁群粒子群混合算法 [J]. 电网技术, 2008, 32(6): 52-56. CHEN Ye, ZHAO Guobo, LIU Junyong, et al. An ant colony optimization and particle swarm optimization hybrid algorithm for unit commitment based on operate coding [J]. Power System Technology, 2008, 32(6): 52-56. [5] DIEU V N, ONGSAKUL W. Improved merit order and augmented Lagrange Hopfield network for unit commitment [J]. IET Gener Transm Distrib, 2007, 1(4): 548-556. [6] 顾锦汶, 杨佰新. 电力系统机组组合优化的快速模拟退火算法 [J]. 中国电机工程学报, 1992, 12(6): 69-73. GU Jinwen, YANG Baixin. The unit commitment by fast simulated annealing algorithm [J]. Proceedings of the CSEE, 1992, 12(6): 69-73. [7] XIA X, ELAIW A M. Optimal dynamic economic dispatch of generation: a review [J]. Electric Power Systems Research, 2010, 80(8): 975-986. [8] FRANGION A, GENTILE C, LACALANDA F. Sequential Lagrangian-MILP approaches for unit commitment problems with general ramp constraints [J]. Int J Elect Power Energy Syst, 2011, 33(3): 585-593. [9] 李颖浩, 郭瑞鹏. 基于广义Benders分解的启发式机组组合优化 [J]. 电网技术, 2012, 36(3): 179-183. LI Yinghao, GUO Ruipeng. A generalized Benders decomposition based heuristic algorithm for unit commitment [J]. Power System Technology, 2012, 36(3): 179-183. [10]SIFUENTES W S, VARGAS A. Hydrothermal scheduling using benders decomposition: accelerating techniques [J]. IEEE Transactions on Power System, 2007, 22(3): 1351-1359. [11]YANG Linfeng, JIAN Jinbao, ZHU Yunan, et al. Tight relaxation method for unit commitment problem using reformulation and lift-and-project [J]. IEEE Transactions on Power System, 2015, 30(1): 13-22. [12]杨濛濛. 大规模风电外送安全稳定控制研究 [D]. 杭州: 浙江大学, 2015. [13]刘纯, 曹阳, 黄越辉, 等. 基于时序仿真的风电年度计划制定方法 [J]. 电力系统自动化, 2014, 38(11): 13-19. LIU Chun, CHAO Yang, HUANG Yuehui, et al. An annual wind power planning method based on time sequential simulations [J]. Automation of Electric Power Systems, 2014, 38(11): 13-19. [14]张宏宇, 印永华, 申洪, 等. 大规模风电接入后的系统调峰充裕性评估 [J]. 中国电机工程学报, 2011, 31(22): 26-31. ZHANG Hongyu, YIN Yonghua, SHEN Hong, et al. Peak-load regulating adequacy evaluation associated with large-scale wind power integration [J]. Proceedings of the CSEE, 2011, 31(22): 26-31. [15]李驰, 刘纯, 黄越辉, 等. 基于波动特性的风电出力时间序列建模方法研究 [J]. 电网技术, 2015, 39(1): 208-214. LI Chi, LIU Chun, HUANG Yuehui, et al. Study on the modeling method of wind power time series based on fluctuation characteristics [J]. Power System Technology, 2015, 39(1): 208-214. [16]ZHAI Q Z, GUAN X H, CHENG J H, et al. Fast identification of inactive security constraints in SCUC problems [J]. IEEE Trans on Power Systems, 2010, 24(4): 1946-1954. (编辑 杜秀杰) Decomposed Unit Commitment Model for Long Term System with Large Scale Wind Power Penetration GONG Benhui,WANG Xiuli,DANG Can,YAO Li,HOU Furui (School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China) The traditional strategy to solve unit commitment problems for large-scale power system usually ignores the optimized model and only focuses the optimized algorithm to accelerate the solving rate. Thus a decomposed unit commitment model is proposed to accelerate the unit commitment, and the wind curtailment density is considered to assess the wind curtailment. In the decomposed unit commitment model, the continuous variables are separated to discrete ones. The model enables to eliminate the feasible solution space, and then the optimal solution can be sought from the narrow space quickly. The wind curtailment density curve gets better than the expected wind curtailment value to assess the distribution of wind curtailment. For the proposed model and the real province power grid, the speeds of traditional unit commitment and the decomposed unit commitment are discussed, and the wind curtailment density curve is employed to estimate the distribution of wind curtailment, on which the system wind curtailment develops from the center to the two sides. wind power; decomposed unit commitment model; unit commitment; wind curtailment density curve; production simulation 2016-01-25。 作者简介:宫本辉(1989—),男,硕士生;王秀丽(通信作者),女,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51577146);国家电网公司科技项目资助(NY71-14-052)。 时间:2016-03-16 10.7652/xjtuxb201606022 TM715 A 0253-987X(2016)06-0143-09 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160316.1001.002.html3 含风电多区域机组组合分解模型
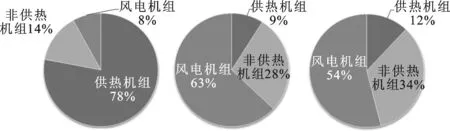
4 算例研究
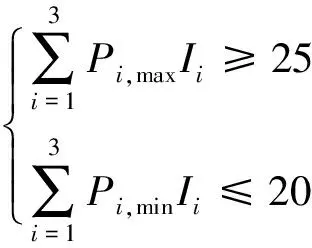
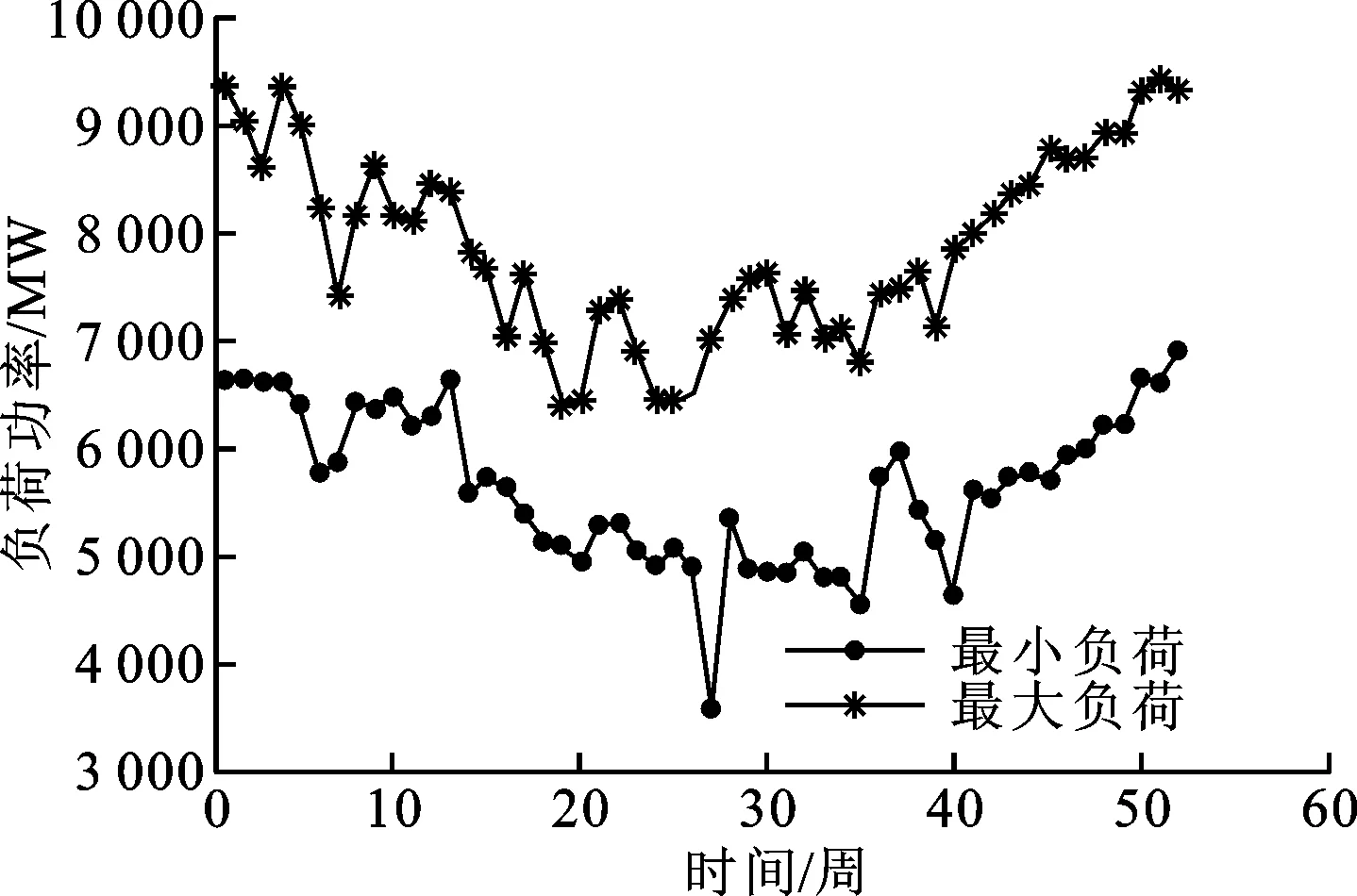
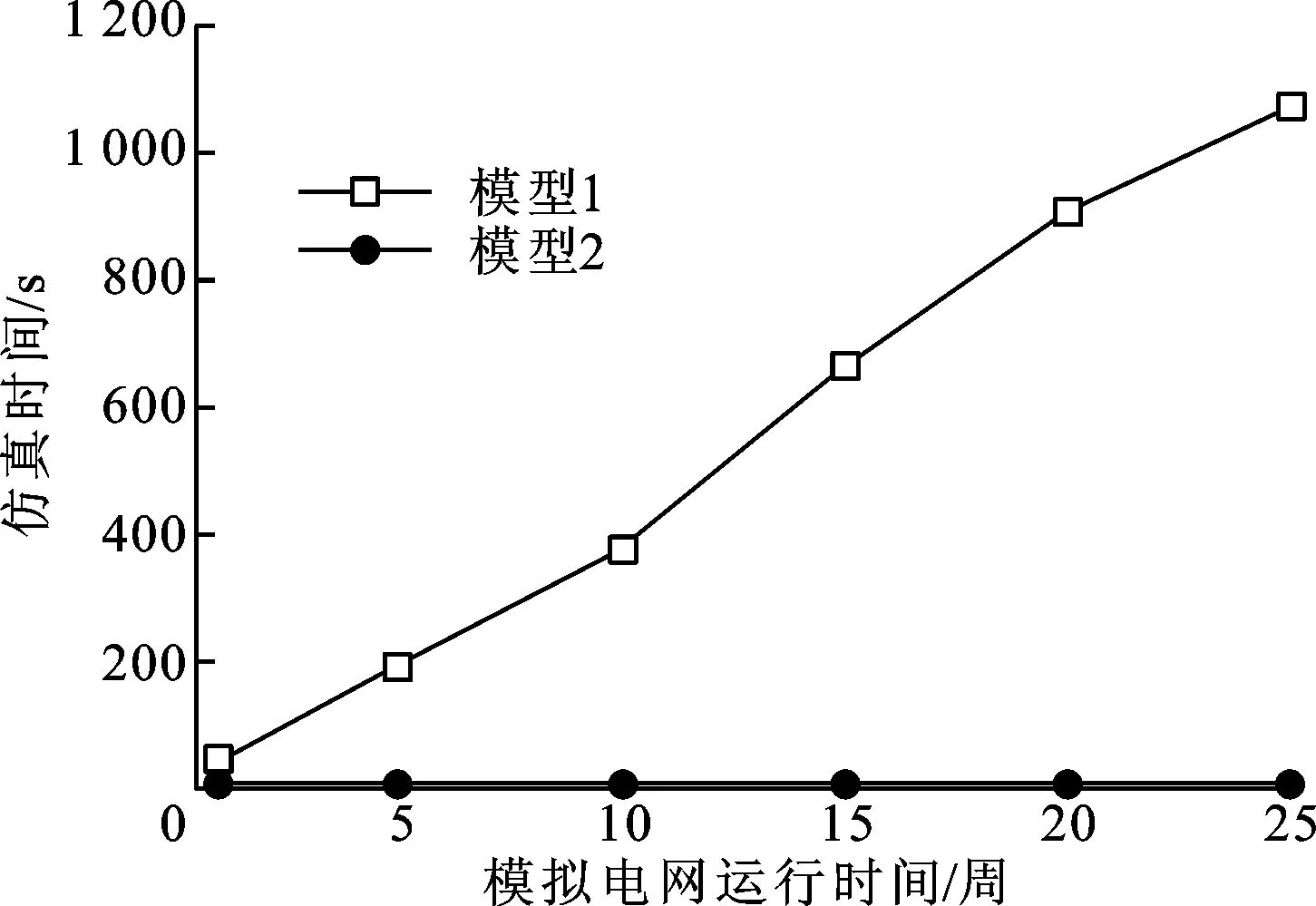
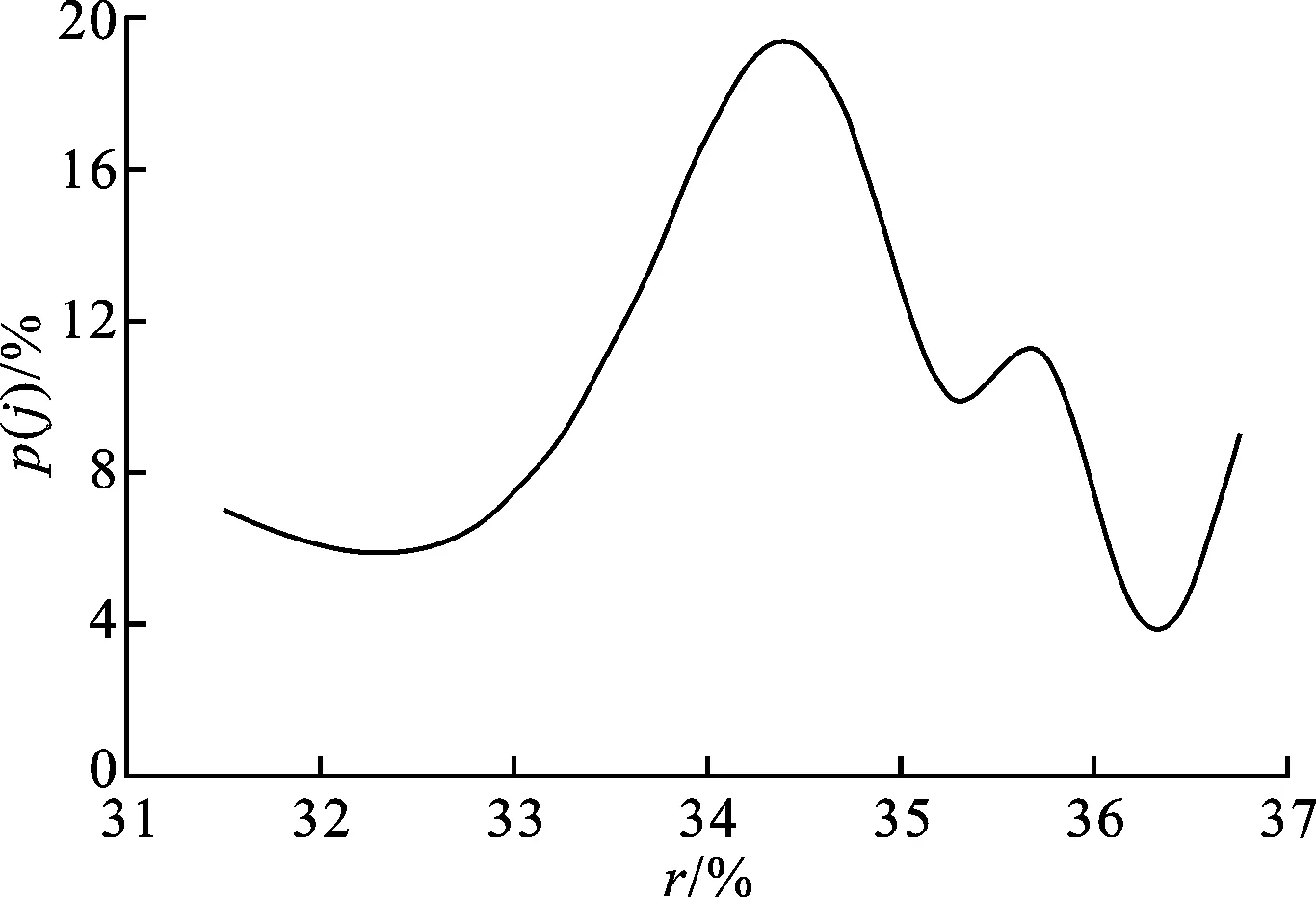
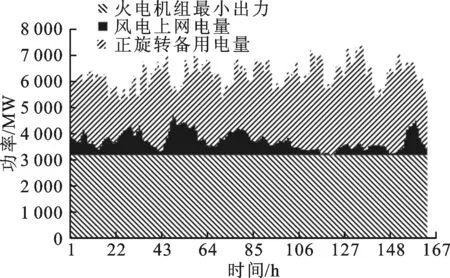
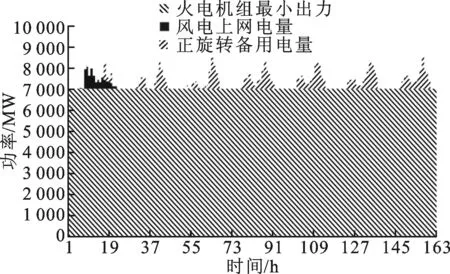
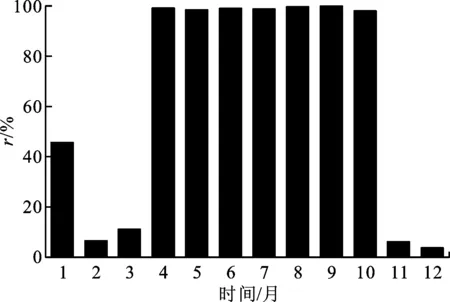
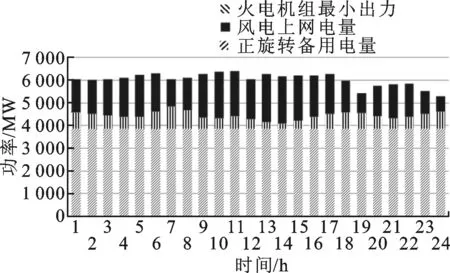
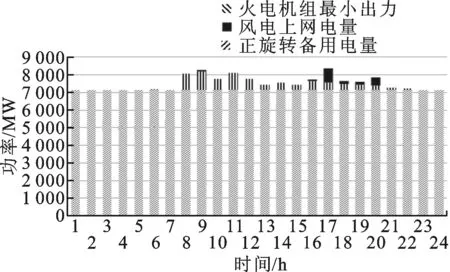
5 结 论
