一种鉴别稀疏局部保持投影的人脸识别算法

杨艺芳,王宇平

(1.西安电子科技大学数学与统计学院,710071,西安;2.西安电子科技大学计算机学院,710071,西安;3.西安石油大学理学院,710065,西安)



一种鉴别稀疏局部保持投影的人脸识别算法

杨艺芳1,3,王宇平2

(1.西安电子科技大学数学与统计学院,710071,西安;2.西安电子科技大学计算机学院,710071,西安;3.西安石油大学理学院,710065,西安)

为解决鉴别稀疏邻域保持嵌入(DSNPE)算法中类间离散度构造复杂的问题,提出了一个新的维数约简算法即鉴别稀疏局部保持投影的人脸识别算法(DSLPP)。首先利用样本集中各类样本的平均向量构造字典,通过保持各类样本平均向量的稀疏重构关系,提出一个新的无参数类间离散度;再通过同时最大化类间离散度和同时最小化类内紧凑度的准则来寻找最优投影方向;最后采用最近邻分类器进行人脸分类识别。由于所采用的类间离散度最大限度地扩大了不同类别中样本之间的差异,因此DSLPP算法具有更强的类间判别力,其识别率得到了明显提高;此外,字典的简化构造降低了算法的计算复杂度。在Yale、UMIST和AR人脸库上的实验结果表明:DSLPP算法在Yale、UMIST库上的平均识别率及AR库上的最高识别率分别达83.38%、95.72%和83.71%,较其他传统方法的识别率有明显提高;在UMIST库上的实验结果表明,DSLPP算法较DSNPE算法的平均计算时间减少了81.7%。

人脸识别;维数约简;稀疏重构;局部保持投影

人脸识别中,往往会遇到“维数灾难”问题,因此维数约简是一种常采用的手段。目前,已经有许多种维数约简方法,根据不同的标准可以有不同的分类,根据映射函数的形式可分为线性和非线性。主成分分析(PCA)法[1]和线性判别分析(LDA)法[2]因其简单高效而成为经典算法,但是PCA和LDA算法都是基于欧氏空间的,主要用于处理线性数据集,不能发现复杂非线性数据集的固有结构。为刻画样本的非线性流形结构,一些能够处理非线性数据集的流形学习算法被相继提出,如等距映射(Isomap)法[3]、拉普拉斯特征映射(LE)法[4]等,但这类方法中非线性映射仅定义在训练集上,对于新的测试集却无法通过此映射降维到低维空间。流形学习方法的线性化能够解决这个问题,代表性的算法有邻域保持嵌入(NPE)法[5]和局部保持投影(LPP)法[6],然而,NPE和LPP法都是无监督算法,没有利用数据点的类判别信息。因此,许多有监督的流形学习算法相继涌现出来,如有鉴别局部保持投影(DLPP)[7]等流形学习算法,然而此类算法的共同缺点是需要人工选择邻域大小参数和边权值参数,而且其性能对这些参数比较敏感。

近年来,基于稀疏表示的方法在人脸识别中得到了广泛应用。2009年,Wright[8]等人提出了基于稀疏表示分类器的人脸识别方法,将稀疏表示成功引入人脸识别领域。随后文献[9-10]也相继提出基于稀疏表示的人脸识别方法,文献[10-11]利用稀疏表示的方法自适应构建L1范数图,无需要任何其他模式参数。稀疏保留投影算法(SPP)[12]是一种以保持数据的稀疏表示结构为目的的较好的维数约简方法,但它是无监督的,未利用类标信息。对此,文献[13]通过利用类标信息对SPP进行了改进,提出鉴别稀疏邻域保持嵌入的算法(DSNPE),获得了较高的人脸识别率,但DSNPE算法中类间离散度构造较复杂,尤其是稀疏表示字典包含数量很大的样本,时间复杂度较高。为了改进该算法的性能,本文提出了一个新的有监督的维数约简算法即鉴别稀疏局部保持投影算法(DSLPP)。该算法用样本集中各类样本的平均向量构造字典,结合稀疏表示和DLPP算法中类间离散度的构造方法,提出新的无参数的类间离散度,有效降低了算法的计算复杂度,增强了算法的判别力。在常用的人脸数据集Yale、UMIST和AR上的测试结果表明,该算法相比其他算法具有更好的识别效果。

1 鉴别局部保持投影算法

(1)

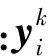
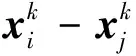
(2)

Bij=exp(-‖fi-fj‖2/t)

(3)

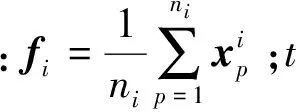
DLPP算法的目标是最小化式(1)中的函数,从而求得最优投影矩阵。

2 鉴别稀疏邻域保持嵌入算法

DSNPE算法是通过最大化类内紧凑度和类间离散度之差来寻找最优投影矩阵。

2.1 类内紧凑度

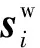
(4)

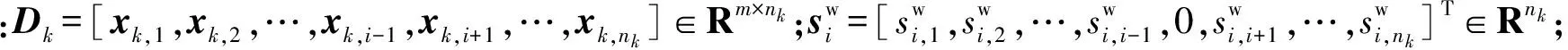
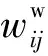
(5)

式中:rk-1=n1+n2+…+nk-1。

通过定义下面的目标函数来构造类内紧凑度

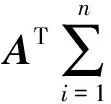
tr(ATXMwXTA)

(6)

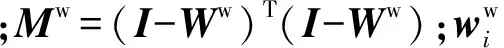
2.2 类间离散度

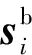
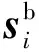
(7)

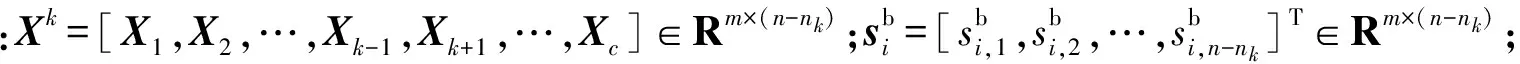
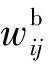
(8)

式中:rk-1=n1+n2+…+nk-1。

通过定义下面的目标函数来构造类间离散度

(9)

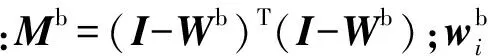
LwXTA)。

3 鉴别稀疏局部保持投影算法

DSNPE算法利用求得的稀疏表示系数创建L1范数图,其近邻参数可以通过稀疏约束自动产生,从而克服了NPE算法中近邻参数设置难的问题,但DSNPE算法的类间离散度构造较复杂。对此,本文结合LPP算法,通过最大化类间离散度和最小化类内紧凑度,提出了DSLPP算法,简化了类间离散度的构造,扩大了不同类数据之间的距离,增强了算法的判别力。

3.1 类内紧凑度

与DSNPE中类内紧凑度相同,Ww表示类内权重矩阵。结合LPP算法,定义类内紧凑度的目标函数为

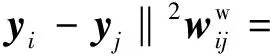
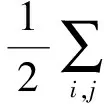
tr(ATXLwXTA)

(10)

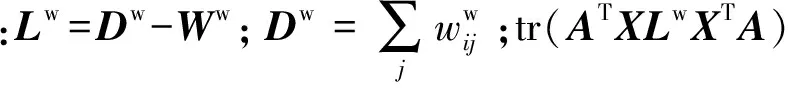
3.2 本文提出的类间离散度

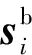
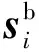
(11)

式中:D=[f1,f2,…,fi-1,fi,fi+1,…,fc]∈Rm×c;

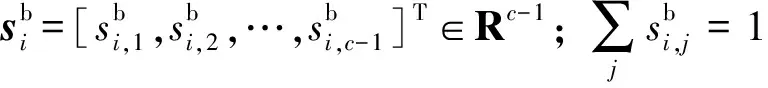
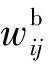
(12)

式中:Wb表示类间离散度矩阵。通过定义下面的目标函数来构造类间离散度

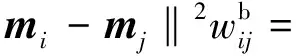
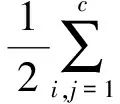
tr(ATFLbFTA)

(13)

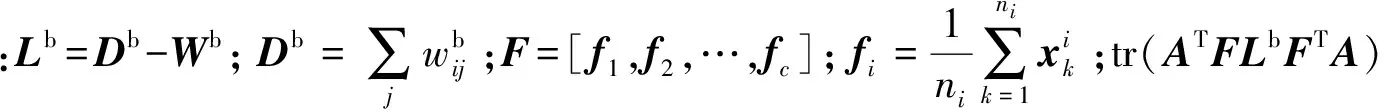
3.3 DSLPP算法

联合考虑类内紧凑度和类间离散度,本文先给出DSLPP算法的目标函数如下

(14)

一般情况下,不能直接得到这个迹比函数的最优解[14]。本文进一步化简式(14),得到DSLPP算法的目标函数

(15)

在分类问题中,当样本维数高、可获得的样本数少的情况下,矩阵XLwXT总是奇异的。为了避免矩阵XLwXT的奇异性,本文首先用PCA对训练样本进行降维。

DSLPP算法的主要步骤可归纳如下。

(2)用式(12)计算类间离散度矩阵Wb。

(3)用式(5)计算类内紧凑度矩阵Ww。

(4)解特征方程FLbFTA=λXLwXTA,则最优投影向量为(XLwXT)-1(FLbFT)的d个最大特征值所对应的特征向量为(a1,a2,…,ad),最优投影矩阵A*=[a1,a2,…,ad]。

(5)DSLPP的最优投影向量ADSLPP=APCAA*。

3.4 时间复杂度分析

DSLPP算法主要是针对DSNPE算法时间复杂度高而提出的新算法。下面是关于这两种算法时间复杂度的比较。

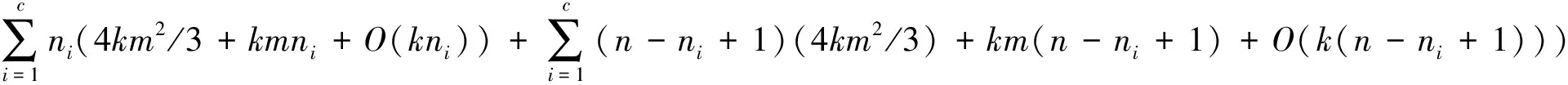
4 实验结果及分析

为了验证算法的有效性,将本文提出的DSLPP算法与其他算法(如LDA、LPP、DLPP、NPE、SPP、DSNPE)在Yale人脸库[16]、UMIST人脸库[17]和AR人脸库[18]上进行实验,并将实验结果进行了比较。这3个人脸库在人脸面部细节、姿态、光照、以及图片背景等方面均存在很大的差异,因此能够很好地检验算法的鲁棒性。为公平比较,将所有相比较的算法首先用PCA方法预处理,对Yale和UMIST人脸库保持98%的图像能量,即保持原数据一定信息的前提下降维;对AR人脸库设置最大约简维数为300。LDA算法最多投影出c-1特征,c为类别个数。对于LPP、DLPP、NPE算法,以步长为1从K=[1,10]区间中搜索最优近邻个数K,热核参数σ为训练样本范数的均值。所有实验都采用最近邻分类器进行分类。实验环境:计算机CPU为Intel(R) Xeon(R) W3505 @2.53 GHz,内存3.98 GB,操作系统Windows XP Professional,操作软件为MATLAB 7.10(R2012a)。

Yale人脸库共有165张人脸图片,每人11张。所有图片被裁剪为64×64像素大小。Yale数据库用来测试有光照、表情变化及有饰物(眼镜)条件下算法的识别性能。实验过程中,对每个人的图片分别随机选样本个数l=4,5,6幅图像进行训练,其余样本用于识别。每个样本数l下重复进行20组实验,最后取20次实验结果的均值作为最终结果进行分析。表1给出了分别采用LDA、LPP、DLPP、NPE、SPP、DSNPE和DSLPP算法在Yale人脸数据库上的平均识别率。图1给出了7种算法在Yale人脸库上的识别结果。

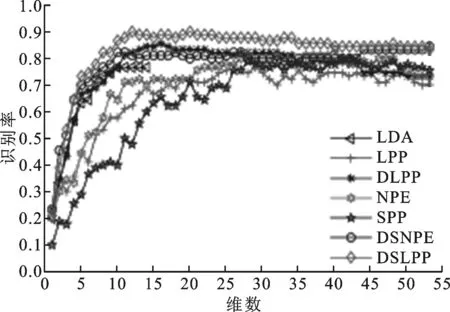
UMIST人脸库由20个不同的人在不同姿势下拍摄的575幅图片组成,每幅图像的大小为112×92像素。每一组图片都有从侧面到正面的不同姿态,这20个图像涵盖了不同种族、性别、面貌特征的情况。实验过程中,对每个人的图像分别随机选取样本数l=5,7,9幅图像进行训练,其余样本用于识别。每个l重复进行20组实验,最后取20次实验结果的均值作为最终结果进行分析。表2给出了LDA、LPP、DLPP、NPE、SPP、DSNPE和DSLPP算法在UMIST人脸数据库上的最高平均识别率。图2给出了7种算法在UMIST人脸库上的识别结果。

AR彩色人脸库包含超过4 000幅的图像,126人,其中男性70名,女性56名。AR人脸库主要包含表情、光照和遮挡等变化,图像分辨率为165×120像素。同文献[19]一样,我们选取一个包含50名男性和50名女性的子库(仅有光照和表情变化),每人选取14张图像,其中7张作为训练样本,剩余7张作为测试样本。为了简化识别过程,将图像裁剪为60×43像素。图3给出了对AR人脸训练的识别结果。表3给出了LDA、LPP、DLPP、NPE、SPP、DSNPE和DSLPP算法在AR人脸库上的最高识别率和对应的维数。

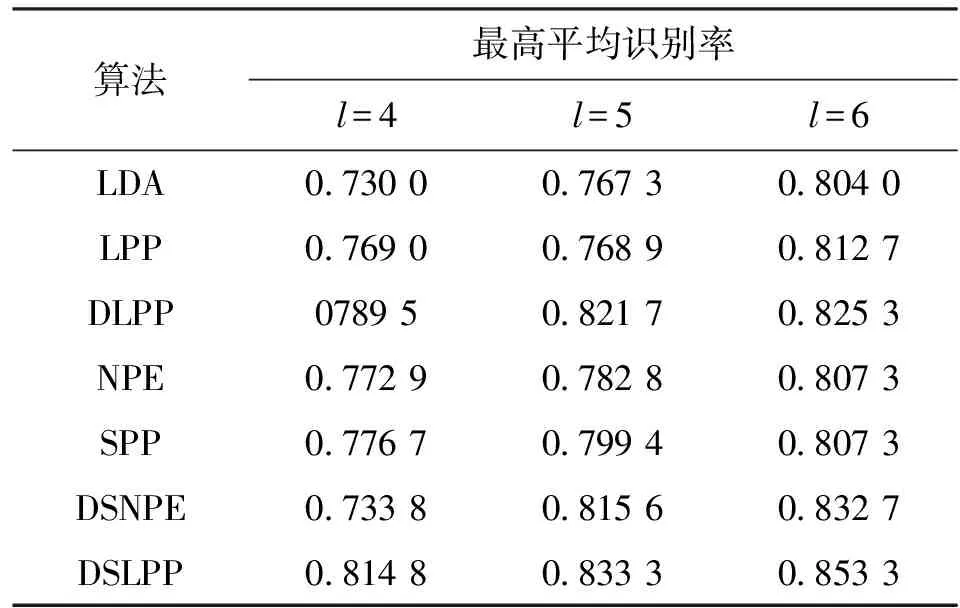
共 表1 7种算法在Yale数据的最高平均识别率

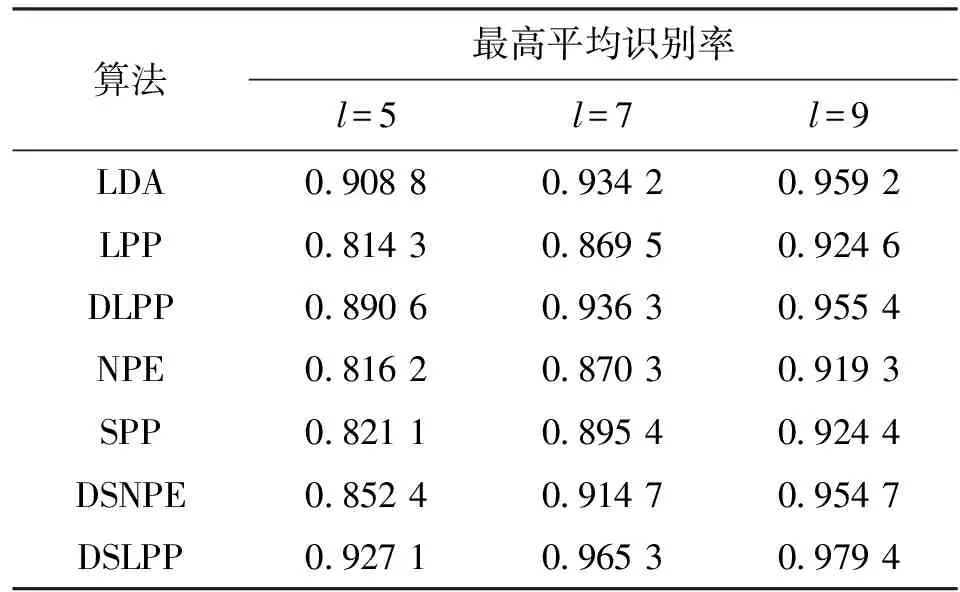
表2 7种算法在UMIST数据的最高平均识别率

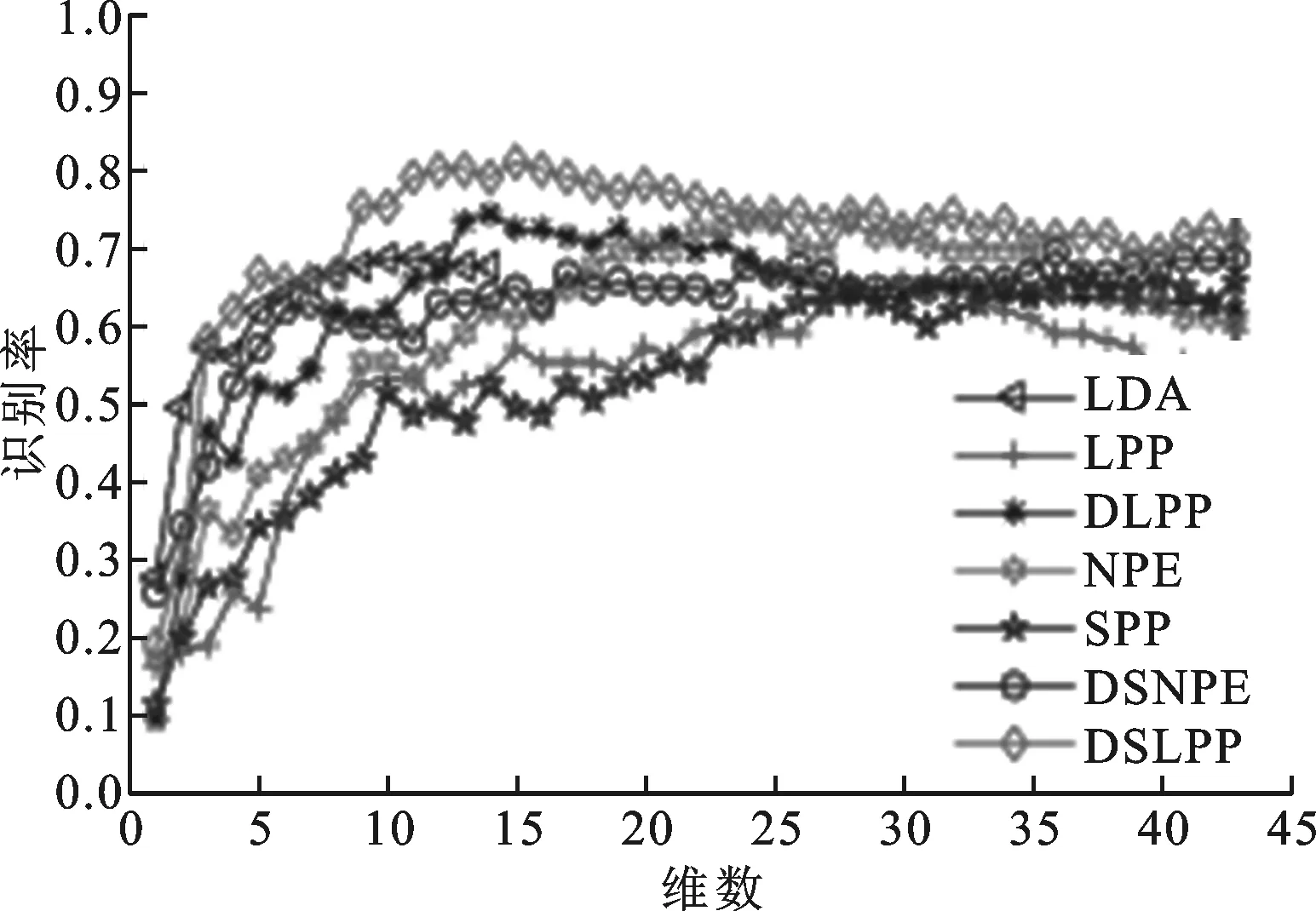
(a)l=4

(b)l=5

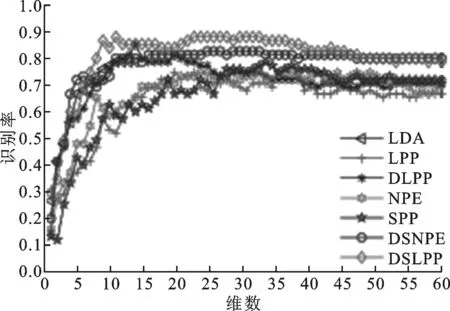
(c)l=6图1 样本数分别为4、5、6时7种算法在Yale人脸库上的识别结果

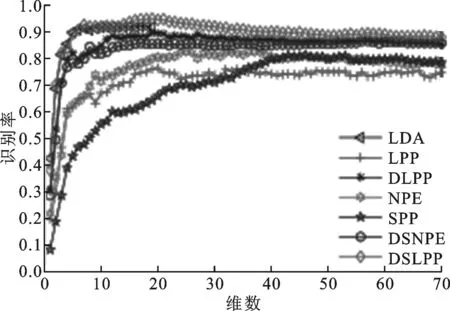
(a)l=5

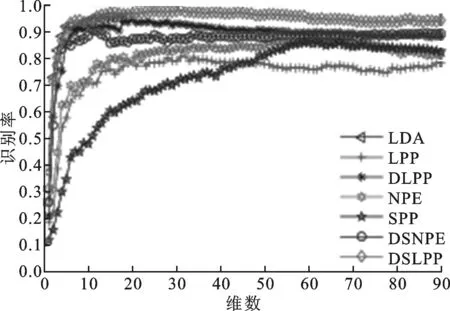
(b)l=7

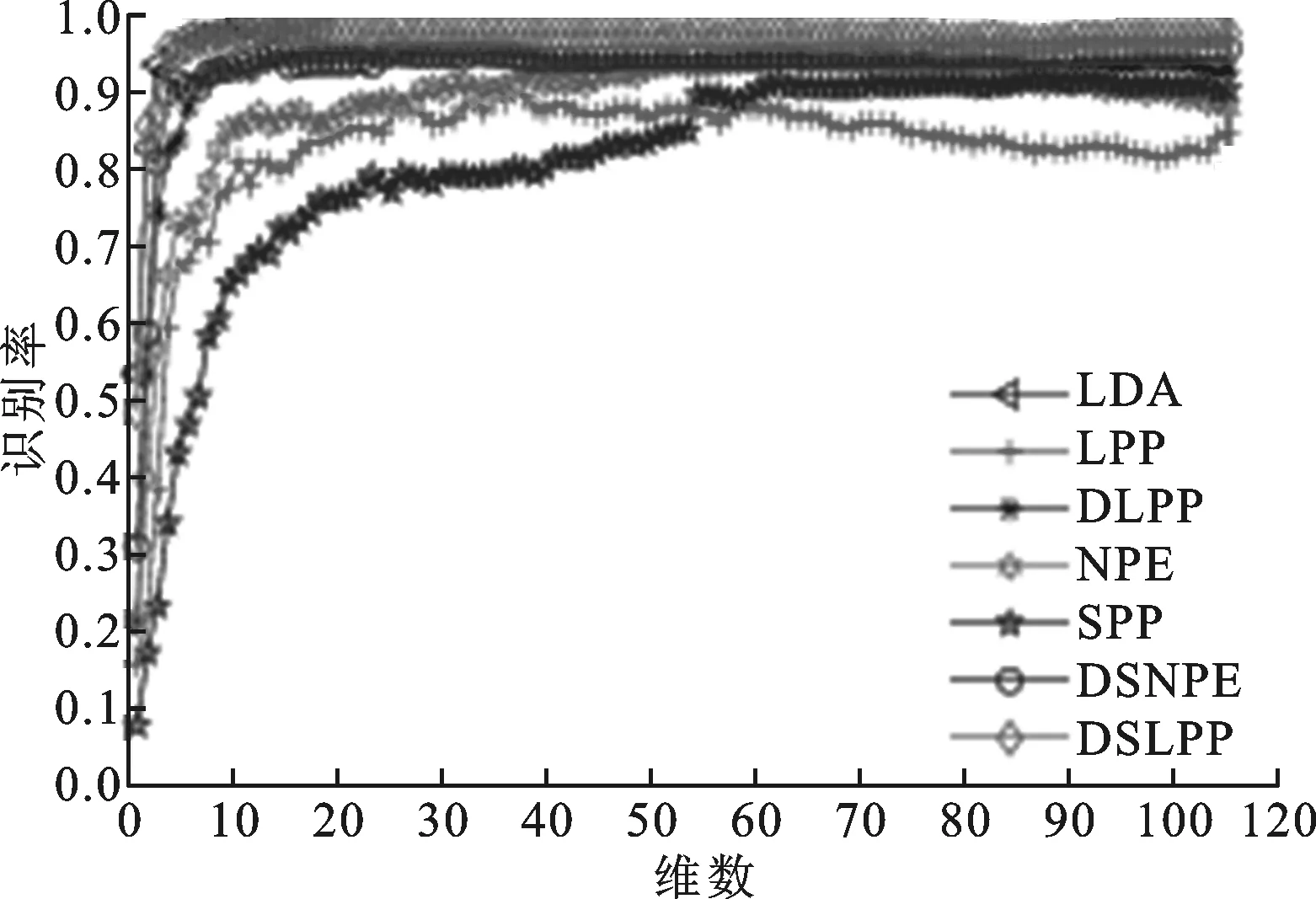
(c)l=9图2 样本数分别为5、7、9时7种算法在UMIST人脸库上的识别结果

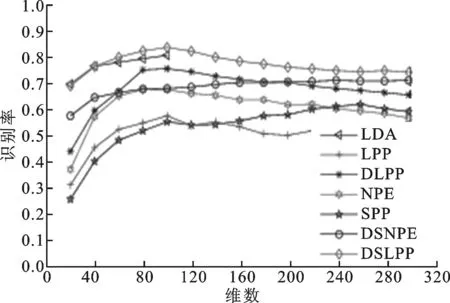
图3 7种算法在AR人脸库上的识别结果

从实验结果可以看出,DSLPP算法在Yale、UMIST 库上的平均识别率及 AR 库上的最高识别率分别达83.38%、95.72%、83.71%,较其他传统方法的识别率有明显提高。LDA、LPP、NPE、SPP算法的识别率相对较低一些,这是因为这3种算法均没有考虑类别信息。虽然DLPP和DSNPE算法均考虑了类别信息,并且都考虑了局部和全局结构信息,但DSNPE算法的识别率高于DLPP算法的,这可能主要因为DSNPE算法是基于稀疏表示法自适应地确定类内类间相似度。与DSNPE算法相比,DSLPP算法获得了更好的识别率,这主要是因为DSLPP算法中所采用的新的类间离散度最大限度地扩大了不同类别中各个样本点之间的差异,从而获得了更好的类间判别力。

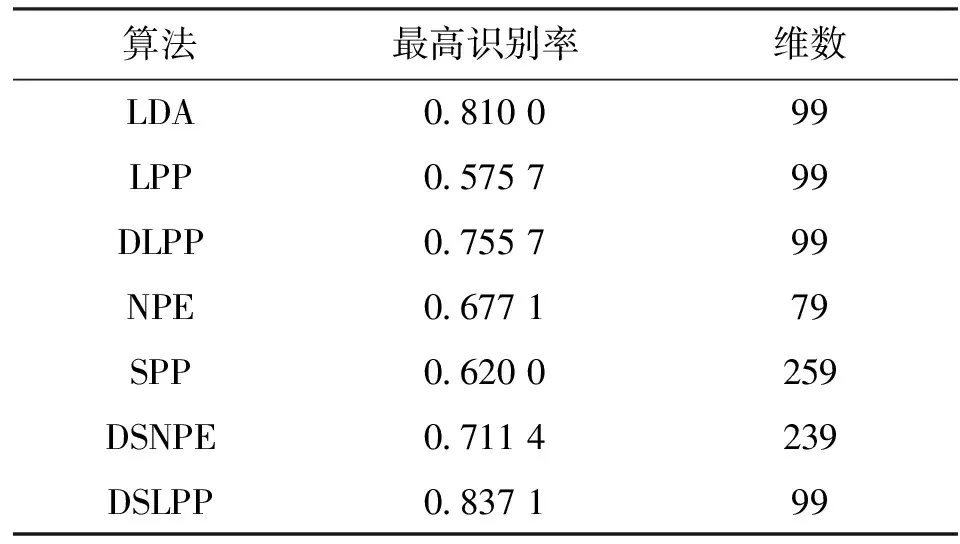
表3 7种算法在AR人脸库上的最高识别率和 对应的维数

在上述所比较的算法中仅有SPP、DSNPE、DSLPP算法采用稀疏表示的方法自适应确定权重矩阵。为了进一步验证本文算法的有效性,对这3种算法在UMIST人脸库上进行了计算时间的比较,实验结果如表4所示。因为SPP算法采用稀疏表示的方法自适应设置了整个样本集的权重矩阵,而DSNPE算法采用稀疏表示不仅设置了类内权重矩阵,而且设置了类间权重矩阵,因此DSNPE比SPP算法耗时。本文所提DSLPP算法也采用稀疏表示方法自适应确定了类内权重矩阵和类间权重矩阵,但正是DSLPP算法中采用了合理的稀疏表示字典设计,从而大大降低了算法的计算时间。从表4可以看出,与SPP和DSNPE算法相比较,DSLPP算法的运行时间明显少得多。

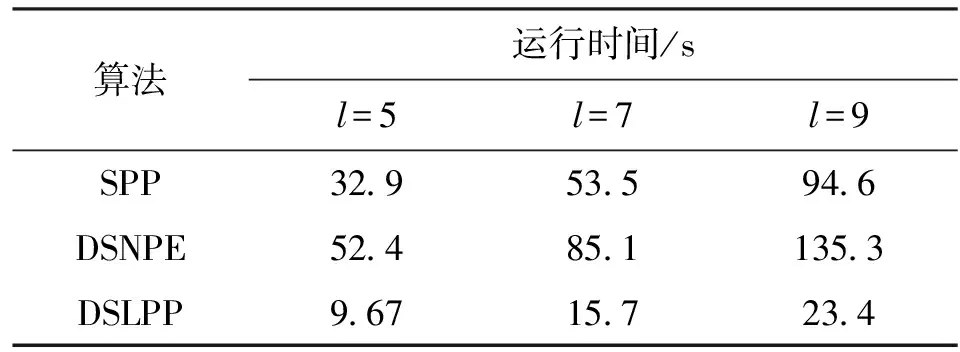
表4 算法运行时间的比较

5 结 论

本文提出了一种新的维数约简的算法,即鉴别稀疏局部保持投影的人脸识别算法(DSLPP)。一方面,DSLPP算法简化了稀疏表示字典的构造,降低了计算时间的复杂度;另一方面,DSLPP算法保持了不同类平均向量的稀疏重构关系,考虑了全局判别结构,扩大了不同类数据之间的距离,算法具有较好判别力。在Yale、UMIST和AR人脸库上的实验表明,DSLPP算法的分类识别结果优于其他方法。今后我们会结合基于概率和Bayesian理论的人脸识别方法对本文方法作进一步的改进。

[1] JOLLIFFE I T. Principal component analysis [M]. Berlin, Germany: Springer-Verlag, 1986: 111-137.

[2] BELHUMEUR P N, HESPANHA J P, KRIENGMAN D J. Eigenfaces vs. fisherfaces: recognition using class specific linear projection [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1997, 19(7): 711-720.

[3] TENENBAUM J B, Silva V D, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction [J]. Science, 2000, 290: 2319-2323.

[4] BELKIN M, NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation [J]. Neural Computation, 2003, 15(6): 1373-1396.

[5] HE X, CAI D, YAN S, et al. Neighborhood preserving embedding [C] ∥Proceedings of the IEEE International Conference on Computer Vision. Piscataway, NJ, USA: IEEE, 2005: 1208-1213.

[6] HE X, YAN S, HU Y, et al. Learning a locality preserving subspace for visual recognition [C] ∥Proceedings of the IEEE International Conference on Computer Vision. Piscataway, NJ, USA: IEEE, 2003: 385-392.

[7] YU W, TENG X, LIU C. Face recognition using discriminant locality preserving projections [J]. Image and Vision Computing, 2006, 24(3): 239-248.

[8] WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227.

[9] 陈思宝, 许立仙, 罗彬. 基于多重核的稀疏表示分类 [J]. 电子学报, 2014, 42(9): 1807-1811. CHEN Sibao, XU Lixian, LUO Bin. Multiple kernel sparse representation based classification [J]. Acta Electronica Sinica, 2014, 42(9): 1807-1811.

[10]WRIGHT J, MA Y, MAIRAL J, et al. Sparse representation for computer vision and pattern recognition [J]. Proceedings of the IEEE, 2010, 98(6): 1031-1044.

[11]杜春, 孙即祥, 周石琳, 等. 基于稀疏表示和非参数判别分析的降维算法[J]. 国防科技大学学报, 2013, 35(2): 143-147. DU Chun, SUN Jixiang, ZHOU Shilin, et al. Dimensionality reduction based on sparse representation and nonparametric discriminant analysis [J]. Journal of National University of Defense Technology, 2013, 35(2): 143-147.

[12]QIAO L S, CHEN S C, TAN X Y. Sparsity preserving projections with applications to face recognition [J]. Pattern Recognition, 2010, 43(1): 331-341.

[13]LU G F, JIN Z, ZOU J. Face recognition using discriminant sparsity neighborhood preserving embedding [J]. Knowledge-Based Systems, 2012, 31(7): 119-127.

[14]JIA Y Q, NIE F P, ZHANG C S. Trace ratio problem revisited [J]. IEEE Transactions on Neural Networks, 2009, 20(4): 729-735.

[15]DONOHO D L, TSAIGs Y. Fast solution of L1-norm minimization problems when the solution may be sparse [J]. IEEE Transactions on Information Theory, 2008, 54(11): 4789-4812.

[16]HE Xiaofei. See [EB/OL]. (2012-02-27)[2015-10-29]. http: ∥www.cad.zju.edu.cn/home/dengcai/Data/FaceData.html.

[17]GRAHAM D B, ALLINSON N M. Characterizing virtual eigensignatures for general purpose face recognition[M]. Berlin, Germany: Springer-Verlag, 1998: 446-456.

[18]MARTINEZ A M, BENAVENTE R. The AR face database, compute vision center technical report #24 [R]. Birmingham, AL, USA: University of Alabama at Birmingham, 1998.

[19]GUI Jie, SUN Zhenan, JIA Wei, et al. Discriminant sparse neighborhood preserving embedding for face recognition [J]. Pattern Recognition, 2012, 45(8): 2884-2893.

(编辑 刘杨)

A Face Recognition Algorithm Based on Discriminant Sparse Locality and Preserving Projections

YANG Yifang1,3,WANG Yuping2

(1. School of Mathematics and Statistics, Xidian University, Xi’an 710071, China; 2. School of Computer Science and Technology, Xidian University, Xi’an 710071, China; 3. College of Science, Xi’an Shiyou University, Xi’an 710065, China)

A new face recognition algorithm, i.e. a discriminant sparse locality and preserving projection algorithm (DSLPP), is proposed to solve the problem that the construction between-class scatters is too complex in the discriminant sparse neighborhood and preserving embedding (DSNPE) method. A novel between-class scatter is constructed by using the mean vector of each class as dictionary and preserving the sparse reconstructive relationship of mean face. Then, an optimal projection matrix is obtained by maximizing the between-class scatter and minimizing the with-class compactness simultaneously. The nearest neighbor classifier is finally used for face recognition. The proposed between-class scatter maximizes the difference of samples between different classes and has more discriminant power, so that the recognition rate of the proposed algorithm is markedly improved. Moreover, the computational complex of the DSLPP algorithm is reduced because of the simple design of the dictionary. Experimental results show that the DSLPP algorithm achieves average recognition rates 83.38% and 95.72% on Yale, and UMIST face database respectively, and a maximal recognition rate 83.71% on AR face database, and that the recognition rates are obviously higher than the recognition rates of some conventional methods. The experimental results on UMIST face databases also show that the average computation time of the DSLPP algorithm is less 81.7% than that of the DSNPE algorithm.

face recognition; dimension reduction; sparse reconstructive; local preserving projections

2015-11-19。 作者简介:杨艺芳(1976—),女,博士生;王宇平(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61503082,61472297)。

时间:2016-04-03

10.7652/xjtuxb201606009

TP391.41

A

0253-987X(2016)06-0054-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160403.1823.008.html