教应有理学需思辨——基于超经验数学研究的“无理数”教学设计

王华（江苏省镇江市丹徒区石马中学）

教应有理学需思辨
——基于超经验数学研究的“无理数”教学设计

王华（江苏省镇江市丹徒区石马中学）

无理数的无限不循环特性超出了日常生活经验的范围，学生难以真正理解.面对这样没有实际情境的数学内容（超经验数学），本节课的设计通过寻找纯数学情境，建立数学知识之间的内在联系，引导学生感受不可公度量，“造”无理数，理性证明无理数等，进而使教与学有理有据.

无理数；超经验数学；生活情境；纯数学情境

一、问题提出

一直以来，中小学数学课堂习惯于通过创设一系列的生活情境，以引发学生的态度体验，从而帮助学生理解所学内容.但是有一些内容超出学生的认知范围，是学生已有经验之外的，仅凭现实生活情境无法达到的数学，即超经验的数学知识，如无理数.由于无法找到实际生活中的情境，往往这部分知识的教学演变成了教师的单向输出，学生只是被动的接受，为了掌握一个概念甚至只能死记硬背.笔者经常思索：这样的教学能给学生留下些什么呢？还有没有更好的方式进行这部分内容的教学呢？

近一段时间，张奠宙教授在“中国数学教育之友初中”群里提出并持续发起了关于“超经验数学”的交流与研讨.笔者有幸参与其中，认真学习并领会张教授关于超经验数学的论述，现结合自己的教学实践，基于超经验数学研究，以“无理数”为例进行教学设计.

二、教材分析

1.教学内容分析

如图1所示.

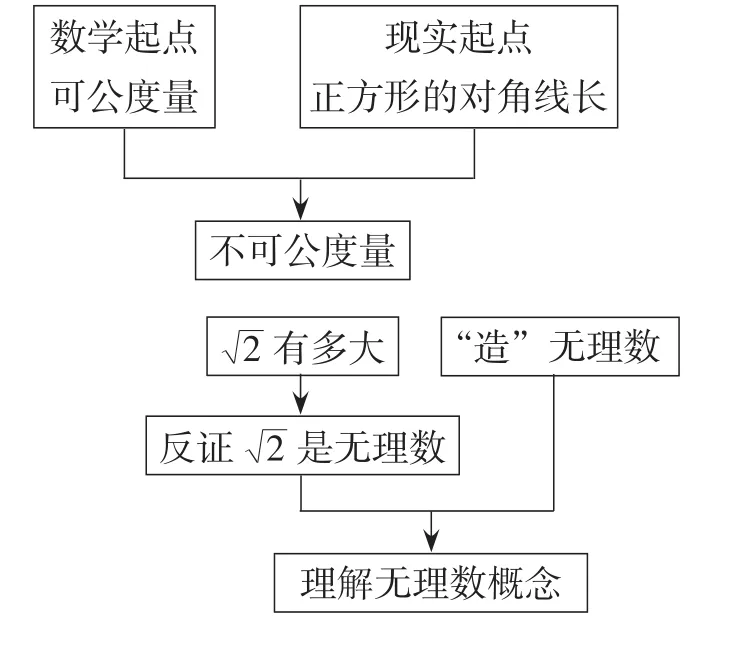
图1

2.教学目标及重点、难点

三、教学过程

1.体验可公度量，定义有理数

活动1：两条线段a和b，能否找到第三条线段c，将线段c当做尺子，使其能以整数次量完线段a和b？

（1）a=6，b=10；

（2）a=0.7，b=1；

（3）教师简单介绍用辗转相减法说明上述线段公度.

辗转相减法：用大数减小数，做一系列减法.例如，（1）10-6=4，6-4=2，4-2=2，2-2=0，即（10，6）→（6，4）→（4，2）→（2，2）最后相减为0；（2）1-0.7=0.3，0.7-0.3=0.4，0.4-0.3=0.1，0.3-0.1=0.2，0.2-0.1=0.1，0.1-0.1=0，即（1，0.7）→（0.7，0.3）→（0.4，0.3）→（0.3，0.1）→（0.2，0.1）→（0.1，0.1），最后相减为0.若上述线段最后相减为0，则两条线段可公度.

师生活动预设：学生自主探究，问题（1）中c为2时，分别3次、5次量完线段a和b，得问题（2）中c为0.1时，分别7次、10次量完a和b，得教师简单介绍辗转相减法，进一步理解可公度量.进而教师引导：能够写成（m，n为整数，n≠0）的数叫做有理数.

【设计意图】很长时间以来，人们一直相信任意两数之比可以转化为两整数之比，在几何上表现为对于任意两条线段，必定存在第三条线段，也许很短，使其能整数次的度量完两条线段.活动1的设置是想让学生经历两条线段可公度的过程，从而定义：我们把能写成（m，n为整数，n≠0）的数叫做有理数，并且体验任意两条线段都是可公度的（尽管这是错误的），为不可公度量的研究做知识上的铺垫.

2.感受不可公度量，“发现”无理数

活动2：将两个边长为1的小正方形沿对角线剪开，可以拼成一个大正方形，求大正方形的边长.此时，能否找到第三条线段，使其能以整数次量完大正方形的边长和小正方形的边长1.

阅读：（1）用辗转相减法求正方形的边与对角线的公度，发现公度根本不存在.

如图2，BC是正方形的一边，AC是对角线，现求两者的公度，先作一次截取：在AC上截取CD=BC，AC截取CD后剩下的一段为AD；第二次截取：做DE⊥AC交AB于点E，易知AD=DE=EB，将BC转化为AB，相当于对BC（实际是AB）作了一次截取，即截BE=AD，剩下线段AE.而剩下的AE正好是以AD为边的正方形的对角线.于是情况又和开始时一样，以下的步骤只是重复上述方式，这种重复永远不会完结.因此不可能存在公度，即AC与AB不可公度.

图2

（2）正五边形、不可公度及无理数.

从图3中看出来，正五边形的一边长度和对角线长不可公度.所谓可公度的思想，其来源是求两整数的最大公约数.a除以b得余数r，继续辗转相除，若到某一步的余数为0，即除尽.两数a，b可公度相当于有“最小公约数”d.但是图中说明，从五边形A1A2A3A4A5到B1B2B3B4B5，再到C1C2C3C4C5，……，这样的过程永远不会完结，即说明正五边形的对角线和边长不可公度.师生活动预设：学生自主阅读，教师适时解读、点拨，进而让学生知道大正方形的边长和小正方形的边长1是不可公度的，也就是说是无法“量”出来的，从而感受阅读材料中图形构造的巧妙及前人的智慧.

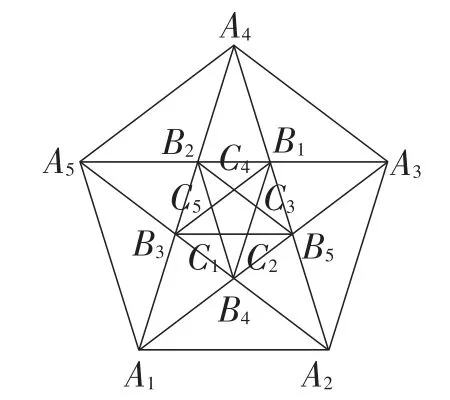
图3

【设计意图】在不少学生看来，有理数已经非常“完美”了，何必要引入无理数呢？除非有充分的理由，而这个理由就是不可公度量的存在.只有让学生真正感受不可公度量的存在，才能切身的体会到无理数学习的必要性.但是这个过程又是非常之难，因为不可公度量的发现本身就是一段传奇.这里通过师生共话一段阅读材料，回顾历史上不可公度量的发现，帮助学生理解不可公度量的存在.

师生活动预设：

师：我们知道，平方后等于2的数应该是一点几，请大家先找一个平方后接近2的小数.

生：1.5.

师：1.52=2.25，比2大.再找一个.

生：1.4.

师：1.42=1.96，比2小了.这说明什么？

师：再找.

生：1.41.

师：1.412=1.9881，比2小，再找.

生：1.42.

师：1.422=2.0164，比2大了，这说明什么.

师：继续找.

生：1.414.

师：1.4142=1.999396，比2小，再找.

生：1.415.

师：1.4152=2.002225，比2大了，这又说明什么.

师：还能再找吗？

生：能！

师：按照这样的方法我们就可以不断地找下去，找到的数的平方会越来越接近2，那么到底等于多少呢？

师：观察计算机的演算结果，同学们有什么发现？

生：我发现算了这么多还没有算完.

生：我发现其结果到目前为止没有出现循环.

师：它们真的是没完没了，又不循环吗？那我们接着继续研究.

活动4：构造一个无限不循环小数.

师生活动预设：

师生共同寻找，如可以写这样一个数.

d=0.10100100010000…（相邻两个1之间依次多一个0）.

生：这个数带有某种规律，但肯定是不循环的无限小数.

师：为什么是不循环的？

生：如果是循环小数，那么一定有有限长的循环节.例如，说是一个100位循环节.可是数d的两个1之间的0，可以不断增加，等到两个1之间出现很多0.例如，一万个0的时候，那时将出现一个循环节里的数全部是0的情况.循环节里都是0，那等于说，某位以后的各个数位全是0，即成了有限小数了.这和d的构造不符.所以，它不能有循环节.

学生尝试构造其他类似的无限不循环小数.

教师总结：我们把这样的无限不循环小数称之为无理数.

师：早在公元前5世纪古希腊的希帕索斯就是这样证明的.叙述不多，理解不难，却很有说服力，我们把这种方法称为反证法.

其实反证法并不神秘.苏轼有一首《琴诗》就是用反证法模式说理的.

若言琴上有琴声，放在匣中何不鸣？若言声在指头上，何不于君指上听？

诗意可以写成如下的命题：琴声不在琴上.

用反证法证明.假设“琴上有琴声”，那么琴放在匣中应该“鸣”.然而这和琴放在匣中的“不鸣”的事实矛盾.因此假设“琴上有琴声”是错的.原命题正确.证毕.

5.回顾探究过程，提炼学习心得

活动6：说一说现在你理解的无理数.

师生活动预设：

师生小结：（1）无限不循环小数是无理数，理解无理数涉及无限，是量不出来的.

【设计意图】通过让学生说出自己关于无理数的理解，畅谈学习中的所思所想，从数学知识、数学素养等维度去感受无理数学习的价值.

四、教学反思

无理数作为超经验的数学知识，教师是无法找寻到一个匹配的生活情境的.因而无理数的学习必须遵循数学内在的发展规律，寻找数学自身内部的需要，创设合理的数学情境，既要让学生了解什么样的数是无理数，即学习无理数相关的知识，更要发挥无理数的教育功能，让学生感受历史上无理数概念形成的艰辛，体验人类孜孜不倦的探索精神，并感悟人类理性获得最终胜利的震撼.数学来自实践，但是又高于实践.数学教学应该注意现实生活情境的创设，但是不必要也不可能每堂课的内容都有生活情境作为背景，很多内容只能以纯粹的数学情境来引入.因此，无理数的教学要注意以下要点.

（1）无理数有现实模型，如单位正方形的对角线，这是学习无理数的入口.

（3）一般地，无理数的定义是无限不循环小数.学生应当知道的“无限”不循环过程是超经验的，无论计算多少位都不会完结.

（4）无理数可以人为地“造出来”，这是超经验的理性思维.

（6）希帕索斯发现无理数是人类理性思维的胜利.

（7）正五边形的边长与其对角线的不可公度性是一个传奇的故事，值得一读.

本设计仅在于为“无理数”这一超经验知识提供一种新的教学思路，通过让学生经历“不可公度量—无限不循环—论证是无理数”的过程，从而把握无理数概念发展的每一个“节点”，直面认知难点，从而让学生真正理顺和讲清无理数的概念，并且感受理性思辨（如反证法）在获取数学知识中的重要作用.当然，对于无理数等超经验数学的理解不可能一蹴而就，通过本设计以期让学生循着一条正确的道路，慢慢的琢磨，不断的加深.例如，其中体现出来的理性思辨甚至应贯穿整个的中学阶段.

数学教师应当创造一种使问题解决得以蓬勃发展的课堂环境.超经验的教学也应当是创设好的数学情境，进而提出问题.弗莱登塔尔说过，数学是人的一种活动，如同游泳，要在游泳中学会游泳，我们必须在创造数学中学习数学.在浩瀚的数学历史中沿着古人的探索脚步，寻找和设计好的问题，不失为进行超经验教学的一种策略.本文问题的设计，环环紧扣，很好地引领学生经历无理数从发现到发展过程中的艰辛曲折，让学生感受无理数发现中一丝不苟的纯粹理性，从而将超经验的无理数置身于自然延伸的数学历史长河之中“再创造”的数学学习.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

2016—09—10

王华（1983—），男，中学一级教师，主要从事数学课堂实效性和解题研究.