在交会处提升能力

姜鸿雁（江苏省无锡市河埒中学）

在交会处提升能力

姜鸿雁（江苏省无锡市河埒中学）

在教学过程中，教师可用整体意识和民主理念引领自己的教学行为，复习课教学亦如此.在教学设计时，于知识点、方法点的交会处，让旧题、旧知识这些“老歌”唱出“新意”，让复习课不再枯燥；在课堂教学时，教师可与学生角色变换，让学生在实现主人翁的挑战中，提升各项能力.复习课如此上，教师在提升自己的同时，把快乐与成就带给了学生.

几何问题；方程思想；知识交会；角色变换；思维共振

笔者2015年6月底参加江苏省无锡市名师评比活动课堂教学环节时，上了一节课题为“品味角平分线”（苏科版《义务教育教科书·数学》七年级下册第七章“平面图形的认识（二）”）的复习课，得到听课教师的一致好评.笔者回顾课堂教学的过程，结合自己对复习课的一些认识，形成文字，期待大家批评指正.

一、课堂实录及说明

师：虽然我们第一次见面，但几天前老师就牵挂你们，猜测你们的复习进度，预测你们的学习状态，相信同学们一定已经厉兵秣马了.今天我们一起重温一位“老朋友”，看看它能给我们带来什么样的思维碰撞.

问题1：在△ABC中，∠A=n.如图1，△ABC的内角∠ABC，∠ACB的平分线相交于点O，求∠BOC的度数（用含n的代数式表示）.

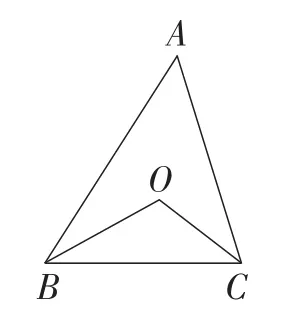
图1

师：为什么？

生1：因为△ABC的内角∠ABC，∠ACB的平分线相交于点O，

师：你用了什么数学思想？

生1：用了整体思想，即把∠ABC+∠ACB，∠OBC+∠OCB看成一个整体.

师：还有不同的解法吗？

生2：如图2，延长BO，交AC于点E.

图2

因为∠BEC=∠A+∠ABE，∠BOC=∠BEC+∠ACO，所以∠BOC=∠A+∠ABE+∠ACO.

因为BO，CO分别平分∠ABC，∠ACB，

师：你用到了什么图形及其结论？

生2：“鱼形”ABOC，结论是∠BOC=∠A+∠ABO+∠ACO.

师：哦，因为它长得像“鱼”，还有不同思路么？

图3

生3：如图3，连接AO并延长，交AC于点D.由此可知∠BOD=∠ABO+∠BAO，∠DOC=∠ACO+∠OAC，所以∠BOC=∠BAC+∠ABO+∠ACO，其余过程与生1相同.

师：你用不同的方法把“鱼形”的结论证明了.借助生3的辅助线，我突然有了一个想法，∠BAO+∠ABO+∠ACO的值是多少？为什么？

生4：应该是90°.因为三角形的三条角平分线相交于一点，点O是两条角平分线交点，则连接线段AO也应该平分∠BAC.

生：哦！那得到本题的数量关系就简单了.

【设计意图】此题让学生从一个非常熟悉的问题入手，引出课题，让学生在“老师”的角色中完成知识的回忆.可是课堂进展到此，在一个个“还有什么不同的思路”的追问中，学生思维并没有运行到笔者预设的轨道——用方程思想解决几何问题，这说明学生在这方面留有空白.同时也说明学生需要引导.生3、生4的表现是本节课意外的生成.

师：还有其他方法吗？角的平分线提供了角与角之间的倍分关系，如果我们用字母表示小角度数的话，那大角的度数将很容易表示；三角形的内角和定理是推理过程中的重要支柱，如果从方程视角来看，则可认为是相等关系；这些将给我们带来什么呢？试试看！

师：如果设∠OBC=x，则……

生：∠ABC=2x.

师：下面的过程哪位小老师能讲下去？

生5：设∠OCB=y，则∠ACB=2y，能得到两个方程：在△BOC中，x+y+∠BOC=180°①，在△ABC中，2x+2y+∠A=180°②.

师：对于这两个方程，我们该怎么办呢？

生：消去x，y.用①×2-②，或者①-②÷ 2，……

师：用方程方法解决几何问题，是解决问题的常用思路.当角与角之间存在倍分关系时，可以通过用字母表示角度，则它们的数量关系就更加明显，使问题解决更加方便.今天让我们在方程思想方法下品味角平分线.

师：这里的未知数x，y的值我们并没有求，那他们的作用是什么？

生：辅助未知数.

师：为了方便记忆、理解和积累经验，把这幅图也起个名字.这是三角形的两条内角平分线，我们就叫它“二内”吧.有“二内”，则会有什么？

生：“二外”.

【设计意图】在众多方法说完之后，又是一个追问“还有其他方法吗？”当学生陷入深思的时候，他们正处在“愤”“悱”状态，教师的一个提示，一个点拨，让学生的思维激起浪花.一道旧题目，给出了新做法，让三角形中的计算与二元一次方程组两部分知识波相遇形成了思维的共振效果.同时，也为解决下面的问题打开了思维的阀门，既是帮助学生理解记忆，又为后面串题成线做好思维的导火线.

问题2：在△ABC中，∠A=n.如图4，△ABC的外角∠DBC，∠ECB的平分线相交于点O′，求∠BO′C的度数（用含n的代数式表示）.

图4

笔者把“二内”“二外”两幅图画在一起，即如图5所示.

图5

师：哪位同学愿意做小老师到台上来讲？

生6：设∠O′BC=x，∠O′CB=y，则∠CBD=2x，∠BCE=2y.得到两个方程：x+y+∠BO′C=180°①，∠A+（180°-2x）+（180°-2y）=180°②.消去x，y，解得

师：两道非常熟悉的问题，在新视角下，对它们却有了全新的认识.在复习过程中，要慢慢学会像这样把所学的知识进行整合重组，以便提升自己解决问题的能力.观察问题1与问题2的结论，有何发现？

观察片刻后，有学生提出：∠BOC与∠BO′C互补.

师：为什么呢？

生7：我是看两个角的表达式，发现两个角的和是180°.

师：不错，能不能结合图形给出证明？

生8到黑板上给出证明，证明过程略.

师：谁能结合平时的解题，提出与三角形角平分线相关的问题来吗？

生9：如图6，BP，CP分别是△ABC的内角∠ABC，外角∠ACF的平分线，∠A=n，求出∠P的度数.

师：太棒了，谁能解决这道题？

图6

笔者把生9所说图形与图5画在了一起，所以呈现在黑板上的是图7.

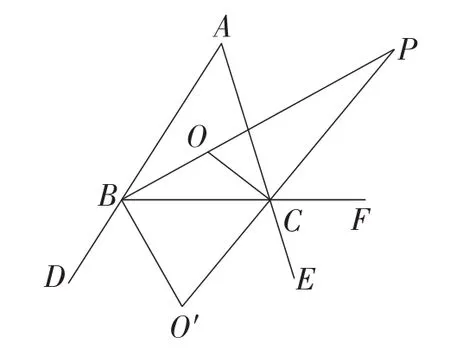
图7

生10到讲台上运用∠ACF，∠PCF分别是△ABC，△PBC的外角，结合方程组很快解决了问题.得∠P=

【设计意图】部分学生能自如地用方程解决熟悉的问题，说明学生已经把方程思想同化到自己的知识体系中了.学生感叹方法的简洁，说明学生认可这个方法，同时让学生感到知识的重组意义多么重大.这正是复习课的意义与价值所在.

师：你们发现∠P与∠O′的关系了吗？为什么？

生11：由刚才的讨论可知，△BPO′是直角三角形，所以∠P与∠O′互余.从表达式也可以看出这一点.

师：很好，从数、形角度都能看出这一点.有一点要做补充说明：图7中，CO′，CP分别是∠BCE，∠ACF的平分线，△BPO′与点B，点O′，点C，点P四个点有关，想想这里有一个什么问题需要交待？

生：O′，C，P三点共线.

生12：CO′，CP分别是对顶角∠BCE，∠ACF的角平分线，对顶角的平分线在同一直线上.

师：很好.这是数学严谨魅力的彰显.到此，我们运用方程思想，将熟悉的结论重新梳理，将熟悉的图形重新整合，发现它们内在的关联性.把一个个零散的题目、结论串起来，有助于我们的记忆和掌握，更有助于提高学习能力，希望同学们将这种学习的方法成为一种经验和习惯.

【设计意图】这个教学环节是对熟悉的结论进行重组和整合，不仅提高了学生的思维能力，也是在暗示学生学会整合知识，注意知识间的关联性，有助于理解与记忆，这是学习方法也是经验积累.

师：刚才都是在三角形中研究问题，我们还要在四边形、多边形中研究；刚才是研究了角的平分线问题，我们还要研究角的三等分线、四等分线……

后面的教学进程，就是把角平分线问题推广到四边形等多边形中，在方程思想的浸润之下，逐一解决.其中有部分问题是学生编写的.

师：时间过得真快，我们合作了一节课，同学们表现很出色.我们要通过这节课学会在复习的过程中整合曾经做过的题目，学会串题成线；重组学过的知识点和数学方法，在这些数学思想和方法的指导下编织知识线条，形成知识网络，并逐步养成良好的思维方式和习惯，相信你们到收获结果的时候一定能满载而归！

【设计意图】当课堂教学运行到这里，已经下课了，没有时间把思维的天地推广到n边形，更没有时间推广到三等分线、四等分线等，甚至连给学生自我总结的时间都没有，笔者只能自己总结，点出本节课的设计意图.

二、教后思考

1.在知识方法交会融合处，提升学生能力

《义务教育数学课程标准（2011年版）》（以下简称《标准》）中明确提出，数学知识的教学，要关注知识的生长点和延伸点，把每节课的知识置于整体知识体系中，注重知识的结构与体系，处理好局部知识与整体知识的关系.所以，教师在教学过程中，要用整体的意识、理念引领自己的教学行为，复习课教学亦如此.用整体的教学目光看，前面所学知识方法为后面的学习做铺垫，后面的知识往往又能反过来促进前面知识的深入理解与提升，相辅相成，互相促进，使学习呈螺旋上升的态势.

这种态势让我们思考：在复习课中，我们除了构建一章章知识框架外，除了讲练习题外，除了纠错外，还要做什么？笔者认为，既然后继学习的知识方法能为前面所学知识注入新的思维活力，那么在复习时，需要用后来学过的方法重新审视曾经解决过的问题，并在此过程中，将曾经解决过的问题重新整合，让它们由原来的点状零散分布，到线状甚至片状分布，让学生有耳目一新之感，让学生感觉复习课不再枯燥，更是提升学生认知能力、思维能力的契机，是对教师教学设计的挑战.

以本节课为例，在知识方法的交会处，我们可以听到思维拔节的声音.上课前，在笔者把学案下发之后，就听到不少学生在下面窃窃私语：这些题目我们以前都做过，又是它们！但在课中，却不时听到“这个方法好简洁！”的感叹，这是学生积极情态的反映，他们还会有“复习课没意思”的想法吗？另外，在教师的点拨之下，学生能够自如地把角平分线与方程（组）内容交织于一体，这不仅是对解决几何图形能力的提高，也是促进方程模型思想的建立，展示了数学知识方法的相辅相成，水乳交融.这种学生思维的拔节态势，反映出学生的解题能力、思维能力就在这个点上得到提升.

培养学生重组知识，要先从教师开始，教师不但要有这个意识，更要有行动.这需要教师要怀着整体教学的意识，沉下心、研教材、深思考，才能具备一双发现知识交会的眼睛，才能改进自己的教学设计，提升自己，成就学生.

2.在师生的角色交会互换中，提升学生能力

《标准》中还明确指出，教师应成为学生学习活动的组织者、引导者、合作者，为学生的发展提供良好的环境和条件.笔者认为，教师的这“三者”角色，不仅体现在课前的教学设计上，还要体现在具体的教学活动中.

在本节课中，在学生能讲题的地方，笔者都给了学生上台表演的机会；学生能编题的地方，笔者鼓励学生编写题目，这时学生是小老师.相反，在学生讲、解题的时候，最需要帮助之处、最需要点拨之地，笔者给他们一架梯子，还原教师角色.本节课就是在教师与学生的角色交会互换中，让学生成为主人，在实现主人翁的挑战中，除了有新发现，更增添一份自信.让学生做主人，这既会给课堂带来意外的生成，更能提升学生的思维和表达能力等综合素质.

具体来说，从讲题角度，对于“二内”这个基本图形及基本结论（如图1中，∠BOC=90°+的教学，几乎都是学生充当小老师的角色在讲解，而笔者不断地提问.在让他们做小老师的同时，笔者更期盼方程思路能从学生口中流露，可是事与愿违.在这过程中，产生了意想不到的生成：复习了三角形角平线相交于一点并随之产生解决这道题的另一思路.在这时，笔者恢复教师的身份，因势利导，给了他们思维一个“支点”.虽然在这个环节里花了不少时间，笔者课前的教学预设也没能完成，但笔者决不因为前面时间花长了而后悔，因为正是在这个民主的过程中，学生积极思考、求知求真的积极情态得到了激发.

从答题角度，教学常态是教师抛出问题，学生解答问题.其实，我们也可以在适当的时候让学生自己编写题目，这不但让学生有主人翁的感觉，更重要的是，在这个过程中，学生的问题意识得到了培养，这一点在复习过程中，价值更加可观.例如，在本节课中，“一内一外”问题的提出，以及把方程思想推广到四边形时，其中部分问题，都是来自学生之口.学生在编写的过程中，已经自觉、不自觉地串题成“线”，整合重组所学内容，逐步达到“会一题，通一类”的境界.课堂的最后，虽然对学生提出的在“n边形和角的三等分线、四等分线”的话题没有时间解决，但是已经给了学生思维飞翔的翅膀.

在复习课中，只有教师对知识再发现、再创造，才能有学生的再发现、再创造；在复习课中，只有学生真正参与的课堂，才是灵动的课堂，不仅有教师的预设，更有来自学生宝贵的生成.在教师的预设中，学生向教师学习；在学生的生成中，教师可以向学生学习.课堂是思维碰撞的场所，为营造这样的场所需要教师和学生一起努力.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京:北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］符永平.老歌新唱浅印深痕：“发现式复习课型”操作体系科学构建的研究与实践［J］.中学数学教学参考（中旬），2009（11）：27-30.

［4］姜晓刚.基于数学实验的三角形的中位线定理的探究：一节江苏省“教学新时空”研讨课的设计与反思［J］.中学数学（初中版），2015（10）：56－59．

［5］邬云德.寓“过程教育”于“认识不等式”教学探索及反思［J］.中国数学教育（初中版），2014（1/2）：68-70.

［6］孙庆民，于彬.基于“导学·反思”教学法的教学案例及几点思考：以“平行四边形的性质（第一课时）”为例［J］.中国数学教育（初中版），2016（6）：46-49.

［7］于彬.基于“两人制暑期集中课例打磨”的实践与思考：以“圆（第一课时）”为例［J］.中学数学（初中版），2015（10）：12-14.

2016—08—15

姜鸿雁（1975—），女，中学高级教师，主要从事课堂教学研究.