水面小尺度漂浮平台的设计与实验
2016-12-23谢克峰李豪杰姚宗辰
谢克峰,张 合,李豪杰,姚宗辰
(南京理工大学 智能弹药技术国防重点学科实验室,南京 210094)
水面小尺度漂浮平台的设计与实验
谢克峰,张 合,李豪杰,姚宗辰
(南京理工大学 智能弹药技术国防重点学科实验室,南京 210094)
针对水面便携、易投放的小尺度漂浮平台的需求,设计了一种基于漂浮系统和稳定机构的水面小尺度漂浮平台,详细分析了水面小尺度漂浮平台的总体结构和工作原理,设计了二自由度的并联稳定机构和基于惯性测量单元的位姿测量系统,建立了基于滑模变结构原理的控制系统。在此基础上,完成了实验室摇摆台实验和水池摇摆实验。实验室实验结果表明,小尺度漂浮平台能够提供±0.2°的稳定基座;水池摇摆实验结果表明,小尺度漂浮平台能够提供±0.8°的稳定基座;负载系统能够有效地探测目标。研究结果可为水面小尺度漂浮平台的改进提供基础。
小尺度漂浮平台;稳定机构;滑模控制;位姿测量
水面小尺度平台是指漂浮在水面上的具有一定承载能力的米级平台。对于安装在水面平台上的各种负载设备,如何确保其稳定、可靠的工作,即保障设备不受外界波浪干扰是水面平台的重要性能指标之一。为了消除波浪运动对负载系统(如激光雷达)造成的影响,通常需要在水面平台上安装稳定机构来实现基座稳定,从而实现负载系统对目标进行可靠、高精度的探测与搜索。水面平台要实现基座稳定,就必须实时的获取平台系统的运动信息,并根据这些信息动态调整基座状态[1]。
目前常见的水面平台研究主要集中在水面舰艇、风电设备等[2-3],石油钻井平台、风电设备这些大尺度资源开采平台平衡稳定性都较好,但是大多具有根基,尺寸较大,控制起来相对复杂,机动性和灵活性比较差。海上无人舰艇装备有先进的控制系统、通信系统等,能够进行海洋侦察和反潜作战,但是其一般都活动在近海海域,整体系统比较复杂。针对水面小尺度平台的研究较少出现,其中Gui Fukun[4]对水面小型浮动养殖网箱动力学响应进行了建模分析,Liu Fushun[5]对具有非零初始条件的海面平台进行了频域内的动力学分析。
本文针对一种水面便携、易投放的小尺度漂浮平台开展了研究,分析了水面小尺度漂浮平台的系统结构和工作原理,设计了稳定机构、位姿测量系统和控制系统。
1 水面小尺度漂浮平台的总体结构
水面小尺度漂浮平台采用立柱式方案。平台由浮囊系统(充气浮囊、弹性连接件)、主体系统(系统电源、航行电机、配重等)、稳定机构(驱动电机、支杆机构、减速器)、负载系统(探测系统,搜索系统)、位姿测量系统和姿态控制与处理单元组成。水面小尺度漂浮平台组成示意图如图1所示。
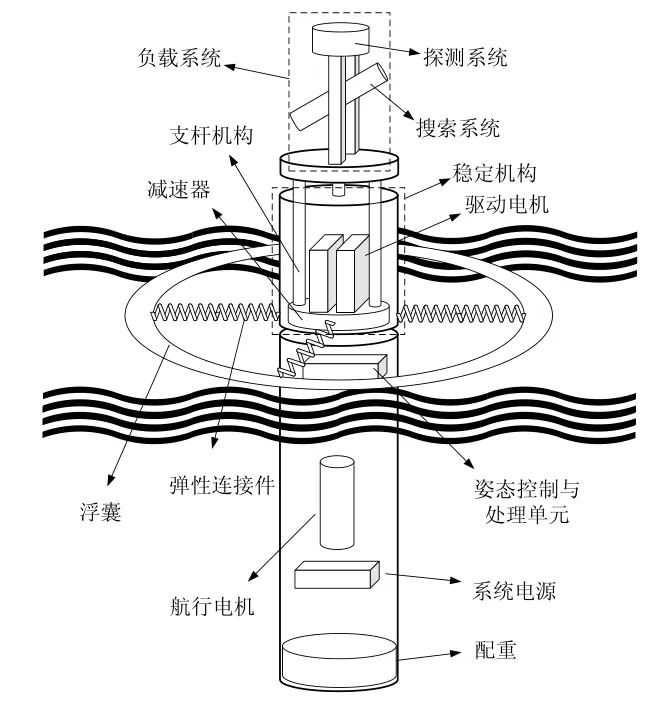
图1 水面小尺度漂浮平台结构示意图Fig.1 Structure of offshore small floating platform
小尺度平台在海面上自由漂浮,若将探测和搜索系统直接安装在小尺度漂浮平台的主体系统上,负载系统就必须随着小尺度漂浮平台的摇摆实时修正基座坐标系,从而增加系统准确探测的难度,降低打击精度。同时稳定的负载系统基座有利于探测与搜索系统获取高质量的外界目标信息,进而有利于减小算法的处理难度和时间。因此将负载系统安装在可抑制海浪摇摆运动的稳定机构上可大大提高负载系统的工作性能。
2 水面小尺度漂浮平台工作原理
水面小尺度漂浮平台工作原理如图2所示。 平台被发射后,在空中或者水下经过一定时间飞行,到达水面后浮囊张开,通过弹性连接件与主体系统连接,提供一定的浮力和回复力,支撑主体系统漂浮在水面上,从而形成水面小尺度漂浮平台。在海浪的扰动下,主体系统和浮囊系统均产生一定的摇摆,引起负载系统基座的水平角度不断变化。位姿测量系统通过惯性测量单元测量负载系统基座和主体系统的两轴摇摆角度和角速度,基于误差补偿原理和四元数算法,采用Klaman融合算法估计负载系统基座当前的摆动姿态角。姿态控制与处理单元利用所估计的姿态角、角速度与系统的目标指令进行比较,通过变结构滑模控制算法获取电机控制量,传输到稳定机构。稳定机构由伺服电机将数字控制量转化为机械位移,通过减速器和支杆机构调整负载系统基座的姿态。负载系统基座姿态的改变由位姿测量系统实时反馈到姿态控制与处理单元,完成系统的闭环控制,实现水面小尺度漂浮平台的目标姿态控制指令。
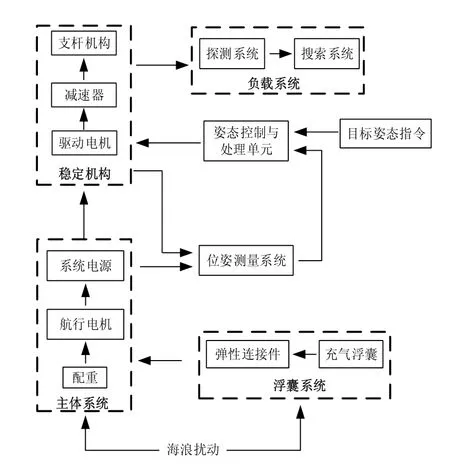
图2 水面小尺度漂浮平台工作原理框图Fig.2 Principle of offshore small floating platform
3 小尺度平台的稳定机构设计
小尺度平台系统通过抑制海洋波浪运动对负载系统基座形成的扰动,控制负载系统基座在不同海洋波浪环境中保持稳定的姿态,实现负载系统的准确定位与目标识别。
在复杂的海浪环境下运动时,小尺度漂浮平台可能产生绕x、y、z三个方向的转动和沿x、y、z三个方向的移动[6]。因此,要完全补偿负载系统基座的运动,需要6自由度的稳定机构。但是,对于小尺度漂浮平台的负载系统而言,其探测距离一般在 5~10 km,小尺度漂浮平台横摇和纵摇的转动角速度一般不大于10 (°)/s,假设探测系统距离探测目标为5 km,则目标点移动的线速度可以达到872 m/s,这会对探测系统的准确度和快速性产生巨大影响。而小尺度漂浮平台在海平面上的移动速度一般在几米每秒,同时z轴的平动位移在±0.5 m内,因此x、y、z三个方向的平动位移对于探测系统的影响可以忽略。应用较多的三自由稳定机构[7]能够实时补偿负载系统在三个方向的姿态变化。但是,对于小尺度平台,其尺寸空间有一定的限制,自由度数量的增加会引起机构复杂且庞大,同时也会引起控制系统处理的数据量急剧增加,严重影响了控制器的处理速度。在保证一定探测精度范围时,补偿小尺度漂浮平台横摇和纵摇的两转动自由度是必要的。忽略回转自由度的影响,回转方向的角位移变化可以通过负载火力系统的随动机构来实现补偿。
因此,本文在保证探测系统精度的情况下,考虑空间限制和数据处理的速度,同时减小稳定机构的复杂程度,采用二自由度(横摇、纵摇)稳定机构实现负载系统基座的稳定。常用二自由度稳定机构包括并联式推杆结构 T-RPT-SPS、2-HUS/U和串联结构[8-10]等多种形式。由于小尺度漂浮平台的稳定机构主要安装负载系统,要求结构简单、紧凑,负载能力强,而2-HUS/U机构结构简单、空间紧凑,采用滚珠丝杆机构,负载能力强。因此文中采用2-HUS/U结构形式。稳定机构包括负载系统基座、支杆机构、驱动电机、齿轮箱和固定架构成。固定架将稳定机构固定在主体系统上,同时支撑各传动部分。负载系统基座连接负载系统,是稳定机构的输出平台,为负载系统提供稳定的探测与搜索基座。支杆机构由支撑杆和滚珠丝杆组成,滚珠丝杆转轴由对应的交流伺服电机驱动,当电机驱动两个滚珠丝杆转动时,通过支杆即可实现负载系统基座在横摇和纵摇两个自由度方向上的转动。
根据小尺度漂浮平台的功能要求,稳定平台应具有以下功能:1)抑制波浪产生的扰动,保持安装在稳定机构基座上的负载系统稳定;2)根据不同海域波浪的波高特性,稳定机构具有一定角度的调节范围;3)根据不同海域波浪的频率特性,稳定机构具有一定频率的调节速度。
4 小尺度平台的位姿测量系统设计
小尺度漂浮平台的位姿测量系统由一组加速度计、陀螺仪和磁强计组成,该组合测姿系统具有重量轻、体积小等特点。该系统可以输出被测平台的两个转动角度、角速度和角加速度等信息。系统采用DSP控制器和 Klaman融合算法,融合多个传感器的原始测量数据,保证在静态和动态环境中均能获得最佳的性能。
位姿测量系统由初始对准算法、信号修正、姿态更新、姿态角估计等组成。陀螺仪与加速度计和磁强计的信号之间具有很强的互补性[11]。先采用陀螺仪信号进行基础解算,再利用加速度计和磁强计的实时解算信号修正陀螺仪的累积积分误差,通过自适应卡尔曼滤波算法,实现信息融合,最终获得高精度的角度、角速度和角加速度信息的估计值。
位姿测量系统分别安装在负载系统基座和主体系统上。安装在负载系统基座上的位姿测量系统主要测量基座的摆动角度,作为控制系统的重要反馈,完成系统的闭环控制。安装在主体系统上的位姿测量系统主要测量主体系统的摆动角速度。作为水面无根平台,在稳定机构调平的过程中,负载系统基座达到目标姿态,而主体系统由于受到调平过程中的反作用力,处于不断摆动的状态。因此,稳定机构的目标并不是单纯追求负载系统基座的最大稳定精度,而必须融合主体系统的摆动信息,在提高稳定精度的同时,保证主体系统处于一种稳定的可接受的运动状态。
5 小尺度平台的控制系统设计
水面小尺度平台的控制系统除了解决运动控制中常见的机械谐振、电机死区、电气参数波动等问题外[12],海浪波动引起的抖振、漂浮系统基座的运动等都会在信号传输、测量和转换的过程中引入大量噪声,降低控制系统的精度和分辨率。同时,负载系统探测和搜索目标的响应时间较短,因此要求控制系统具有快速的动态响应、高质量的稳定精度和对环境参数变化的自适应能力,常规的PID算法很难达到理想的控制效果。
变结构滑模控制是一种特殊的非线性反馈控制系统,是解决有界不可测扰动、系统变参数和模型不确定问题的有效方法。由于滑动模态可以进行设计且与环境参数和扰动无关,使得滑模变结构控制具有快速响应、对参数变化不敏感等优点。将其应用到水面小尺度平台系统中可以解决系统控制快速性和高精度之间的矛盾,增强系统的鲁棒性[13]。基于滑模变结构控制的位姿闭环控制框图如图3所示。
图3中,VSC为滑模变结构控制器,d为海浪扰动角,0θ为负载系统基座的目标位置,pθ为负载系统基座的实时位置。
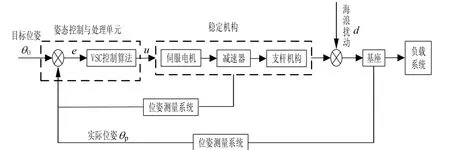
图3 位姿闭环控制框图Fig.3 Block diagram of closed-loop pose control
5.1 滑模控制器的设计
滑模变结构控制的基本思想就是强迫系统的状态变量达到并沿着一条预先规定的相轨迹变化,达到系统平衡位置。定义系统的状态变量x1和x2为

设计控制器使状态变量x1和x2趋于0,选取一阶滑模面:
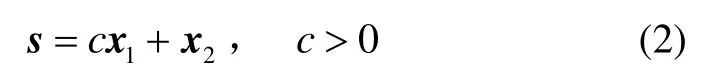
稳定机构的动力学方程经过变换后可以表示为
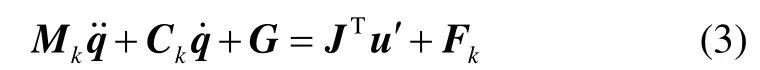
则将式(3)带入滑模面的微分方程:
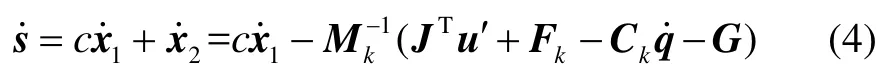
以下利用李雅普诺夫理论[14]来计算控制律,取李雅普诺夫函数为则:
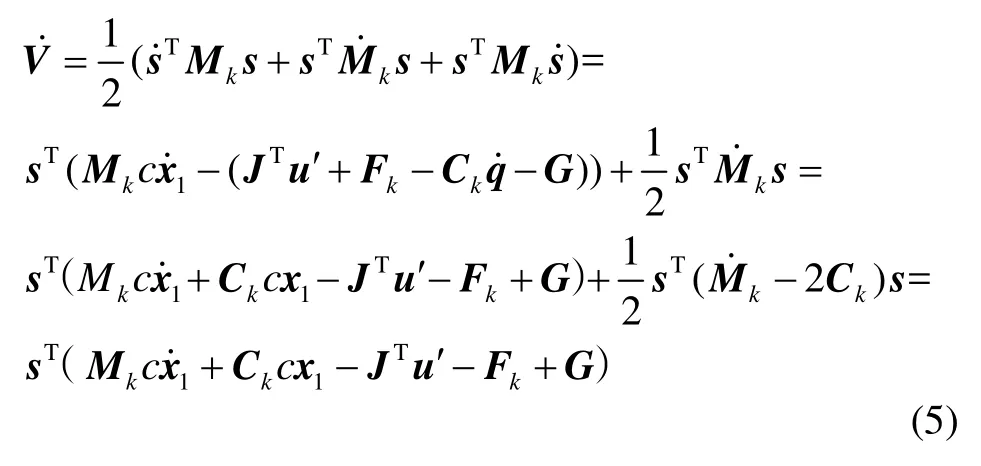
基于式(5),设计控制律为

由于机械结构和电机响应在时间和空间上的滞后,滑动模态会伴随一定的抖振。为了削弱抖振,采用饱和函数sat(s)代替理想函数sgn(s)的准滑模动态控制,饱和函数sat(s)定义为
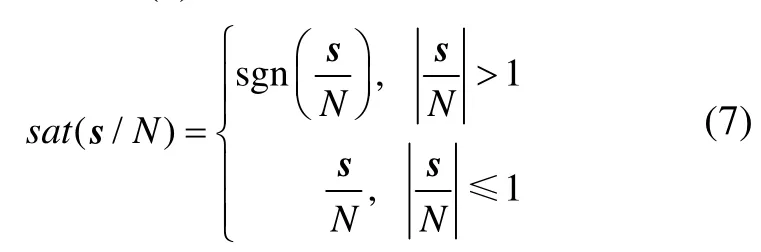
其中N称为“边界层”厚度。则相应的控制律转化为
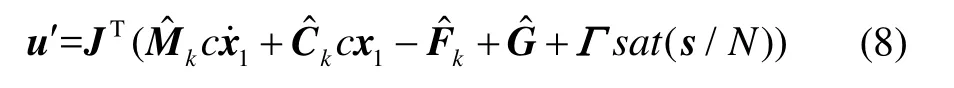
5.2 稳定性的分析
滑模运动过程中分为趋近模态和滑动模态,因此只要满足趋近阶段,进入滑动模态后保持稳定,则可以保证系统稳定性。
将控制律(8)带入李雅普诺夫函数(5)得:

在适当的范围内,只要Γ取得足够大,可以保证VSC趋近模态达到条件V˙<0,即能保证系统进入滑动模态。在滑模面内,若s=0,则系统满足全局渐进稳定。结合滑模面方程(2),得:

进一步得:
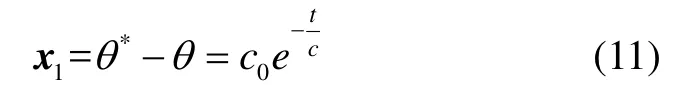
式中,c0为常数。t趋于无穷时,x1趋近于 0,小尺度平台负载系统基座的实际位姿无限趋近于目标位姿,能够实现系统稳定。其快速性和鲁棒性主要由滑模面参数c决定,受外界的扰动和参数影响较小,因此系统具有较好的稳定性和抗干扰能力。
6 原理样机的设计与实验
按照以上设计,研制了水面小尺度漂浮平台原理样机。已研制的水面小尺度漂浮平台原理样机具有2个稳定自由度,由2个并联伺服电机驱动,在负载系统基座和固定架轴向位置上安装位姿测量系统。平台目标位姿设置为 0°,即基座保持水平稳定。该平台主要用于实现两轴的转动调平,采用文中设计的位姿闭环控制系统进行控制,各构件的估计参数由三维建模软件获得。
对原理样机分别进行了实验室摇摆台实验和水面摇摆实验。水面摇摆实验在6 m×6 m×3 m实验水池中进行,如图4所示。实验室摇摆台实验在单轴摇摆架上进行,为了测试两轴调平稳定的效果,在安装小尺度平台时,将稳定实验台的转动轴对准稳定机构的两个调平轴的角平分线方向,通过摇摆台人工输入一定频率和幅度的摇摆摇动,实验结果如图5所示。探测设备采用红外探测,被探测目标距离小尺度平台 200 m,人工输入扰动模拟由海浪引起的小尺度平台摆动,实验结果如图6所示。
图5为小尺度漂浮平台的摇摆台运动曲线,从图中可以看出,x轴和y轴输入扰动曲线的摇摆角度为4°和6°,频率为0.12 Hz,经过稳定机构后,负载系统基座的稳态精度为±0.2°,有效抑制了输入扰动;图6为小尺度漂浮平台的水面运动曲线,从图中可以看出,x轴和y轴输入扰动曲线的摇摆角度分别为8°和6°,频率为0.4 Hz,经过浮囊系统和稳定机构后,负载系统基座的稳态摇摆角度为±0.8°,在一定程度上抑制了输入摇动,但是与摇摆台实验相比,小尺度平台的水面稳态摇摆角度增大,原因是小尺度漂浮平台在水面上漂浮时,属于无根系统,其稳定过程要更加复杂,同时其各项参数真实值的获取也更加困难。因此,同一套控制系统,在水面实验的精度要比在实验室摇摆台上低。同时,在稳定摇摆角度为0.8°的基座上,负载系统红外探测系统能够有效探测到200 m处的目标,满足系统的探测需求。

图4 小尺度漂浮平台水面测试实验Fig.4 Water surface test experiment of small floating platform

图5 小尺度漂浮平台的摇摆台运动曲线Fig.5 Motion curves of small floating platform on sway platform
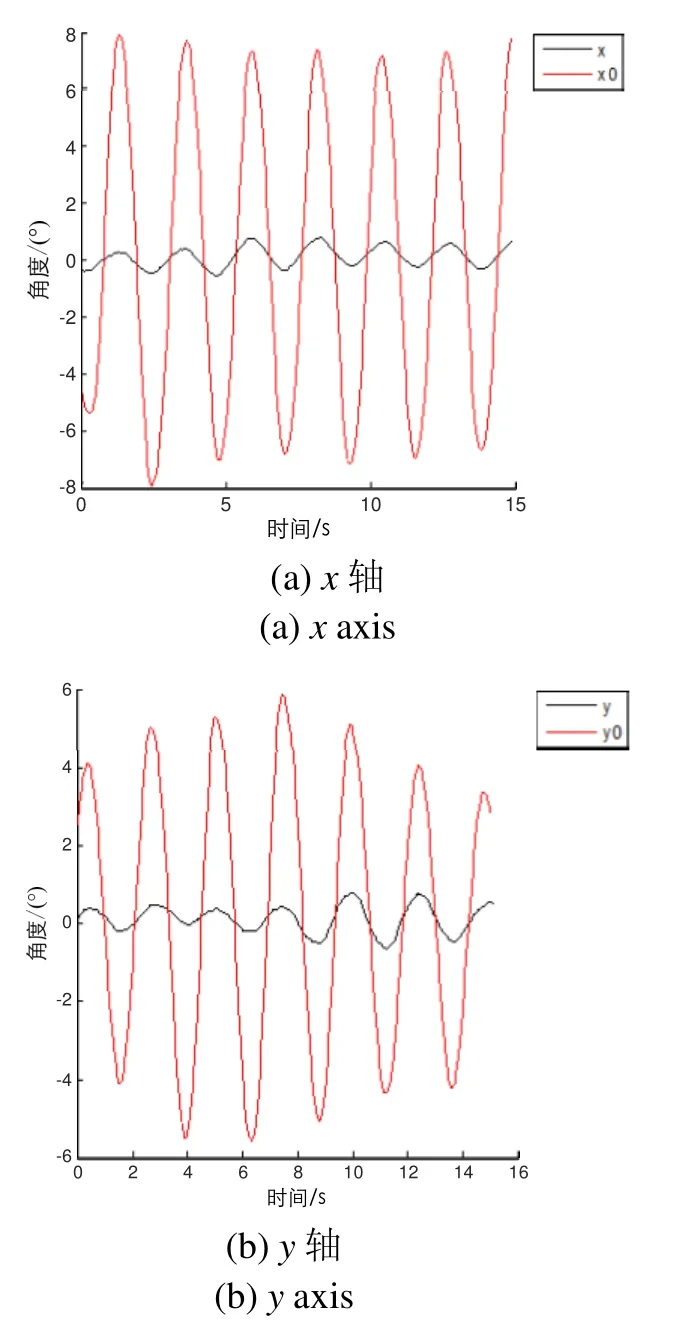
图6 小尺度漂浮平台水面运动曲线Fig.6 Motion curves of small floating platform on water surface
7 结 论
基于便携、易投放的特点,设计了可有效隔离海面波动和提供稳定基座的水面小尺度漂浮平台,详细分析了小尺度漂浮平台的系统结构和工作原理。通过分析海浪对负载设备探测精度的影响,基于2-HUS/U结构设计了并联稳定机构,综合惯性测量单元和Klaman融合算法设计了位姿测量系统,根据稳定机构的动力学方程设计了滑模变结构控制系统。在此基础上,为验证小尺度漂浮平台的基座稳定性,开展了实验室摇摆台和水面调平实验。实验结果表明,在摇摆台上,小尺度漂浮平台能够提供±0.2°的稳定基座,在水池中能够提供±0.8°的稳定基座,同时负载系统能够有效地探测目标。研究结果可为水面小尺度漂浮平台的改进提供参考。
(References):
[1]甘进. 海上多功能工作平台结构设计关键技术研究[D]. 武汉: 武汉理工大学, 2012.
[2]陆欣, 谭乐祖, 高传斌. 水面舰艇平台防空作战能力指标体系与评估[J].舰船电子工程, 2012, 32(9): 23-25.Lu Xin, Tan Le-zu, Gao Chuan-bin. Index system and evaluation on air defense combat capability of single ship platform[J]. Ship Electronic Engineering, 2012,32(9): 23-25.
[3]Hao C, Johnson M H, Aliprantis D C. Low-frequency AC transmission for off-shore wind popower[J]. IEEE Transaction on Power Delivery, 2013, 28(4): 2236-2244.
[4]Gui Fu-kun, Zhao Yun-peng, Xu Tiao-jian, et al. Numerical simulation of dynamic response of a net cage for flatfish in waves[J]. China Ocean Engineering,2014, 28(1): 43-56.
[5]Liu Fu-shun, Lu Hong-chao, Li Hua-jun. Dynamic analysis of offshore structures with non-zero initial conditions in the frequency domain[J]. Journal of Sound and Vibration, 2016, 366: 309-324.
[6]Keller J A, Smith E C. Experimental and theoretical correlation of helicopter rotor blade-droop stop impacts[J]. Journal of Air craft, 1999, 36(2): 443-450.
[7]Li Yang-min, Wu Zhi-gang. Design, analysis and simulation of a novel 3-DOF translational micromanipulator based on the PRB model[J]. Mechanism and Machine Theory, 2016, 100: 235-258.
[8]王海东, 毕玉泉, 杨超, 等. 一种二自由度并联摇摆台运动分析与仿真[J].科学技术与工程, 2011, 23(11): 5660-5663.Wang Hai-dong, Bi Yu-quan, Yang Chao, et al. Kinematics analysis and simulation of the two degrees of freedom parallel tilter[J]. Science Technology and Engineering, 2011, 23(11): 5660-5663.
[9] 谢克峰, 张合, 李豪杰, 等. 海上漂浮2-HUS/U并联平台动力学分析[J]. 农业机械学报, 2016, 47(1): 362-368.Xie ke-feng, Zhang He, Li Hao-jie, et al. Dynamic analysis of offshore floating 2-HUS/U parallel platform[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(1): 362-368.
[10]Zou Ying, Lei Xu-sheng. A compound control method based on the adaptive neural network and sliding mode control for inertial stable platform[J]. Neurocomputing, 2015, 155: 286-294.
[11]满益明, 陈慧岩, 胡玉文, 等. 智能车辆捷联视线稳定跟踪平台设计与实现[J]. 中国惯性技术学报, 2009, 17(4): 397-402.Man Yi-ming, Chen Hui-yan, Hu Yu-wen, et al. Design and implementation of intelligent vehicle strapdown line-of-sight stabilization pointing platform system[J]. Journal of Chinese Inertial Technology, 2009, 17(4): 397-402.
[12]Tavakoli M, Lopes P, Sgrigna L, et al. Motion control of an omnidirectional climbing robot based on dead reckoning method[J]. Mechatronics, 2015, 30: 94-106.
[13]王宣银, 程佳. 4TPS-1PS四自由度并联电动平台动力学建模与位姿闭环鲁棒控制[J]. 浙江大学学报(工学版), 2009, 43(8): 1492-1496, 1548.Wang Xuan-yin, Cheng Jia. Dynamic modeling and robust control in task space of 4-DOF parallel electric platform with 4TPS-PS structure[J]. Journal of Zhejiang University(Engineering Science), 2009, 43(8): 1492-1496, 1548.
[14]Barros C J B, Rocha V H L. Attraction and Lyapunov stability for control systems on vector bundles[J]. System and Control Letters, 2016, 92: 28-33.
Design and experiment of offshore small floating platform
XIE Ke-feng, ZHANG He, LI Hao-jie, YAO Zong-chen
(Ministerial Key Laboratory of Zhi Neng Dan Yao, Nanjing University of Science and Technology, Nanjing 210094, China)
An offshore small floating platform based on floating system and stabilizing mechanism was designed which is offshore portable and easily thrown. Its overall structure and principle were analyzed,and a 2-D parallel stabilizing mechanism and an IMU-based pose measurement system were designed. The control system with sliding mode variable structure was set up. Based on these, the swing platform experiment and offshore swing experiment were carried out. Experiment results show that the small floating platform can provide a stable base with ±0.2° precision, the small floating platform can provide a stable base with ±0.8° precision, and the load system can effectively detect the target. The study results provide a basis for the improvement of the offshore small floating platform.
small floating platform; stabilizing mechanism; sliding mode control; position and attitude measurement
TJ67;TH122
A
1005-6734(2016)05-0595-05
10.13695/j.cnki.12-1222/o3.2016.05.007
2016-06-12;
2016-09-13
国家自然科学基金(51475243);江苏省普通高校研究生科研创新计划(KYLX15-0340)
谢克峰(1988—),男,博士研究生,从事水面小尺度漂浮平台姿态稳定控制研究。E-mail: xiekefeng.ok@163.com
联 系 人:张合(1957—),男,教授,博士生导师。E-mail: hezhangz@mail.njust.edu.cn
