直线型和弯曲型纳米碳管特性对纳米复合材料有效力学性能的影响

宋瑞兰， 罗冬梅， 谢 悦， 宿晓如

(佛山科学技术学院 土木工程系， 广东 佛山 528000)



直线型和弯曲型纳米碳管特性对纳米复合材料有效力学性能的影响

宋瑞兰， 罗冬梅， 谢 悦， 宿晓如

(佛山科学技术学院 土木工程系， 广东 佛山 528000)

在ANSYS平台构建直线型和弯曲型的实心和空心纳米碳管增强陶瓷基复合材料的三维特征体积单元模型. 利用双尺度渐近均质化理论计算复合材料的有效力学性能， 分析纳米碳管的几何形状和力学特性对复合材料有效刚度的影响. 分析结果表明， 随着长度和直径的变化， 实心纳米碳管与空心纳米碳管增强复合材料的有效力学性能效果差异较大， 两者具有不可替代性. 而且纳米碳管的各向异性明显导致有效刚度降低， 忽略纳米碳管的各向异性会高估复合材料的有效力学性能. 此外， 纳米碳管的弯曲程度对横向有效弹性模量和有效剪切模量有较显著的影响. 正确构建纳米碳管模型， 合理选择纳米碳管的形状和尺寸对准确评估纳米碳管增强复合材料的有效力学性能有重要意义.

纳米碳管； 纳米复合材料； 有效刚度； 双尺度均质化法

0 引 言

近年来， 纳米碳管以特殊的结构和优异的性能已成为新型材料的代表， 并成为复合材料增强相的理想选择. 以纳米碳管为增强相的复合材料， 已经在金属基、 高分子基的材料中取得了比较显著的效果[1-2]， 目前国内外学者围绕纳米碳管增强复合材料进行了一系列的研究. 利用经典Mori-Tanaka理论[3-4]、 分子动力学与连续体力学相结合[5-6]以及多尺度均质化[7-9]等方法， 已发现纳米碳管的长径比、 体积含量、 形状、 排列方式以及弹性模量等都会对复合材料的有效力学性能产生不同程度的影响， 实际上这些研究大部分是利用连续介质力学原理将纳米碳管简化为实心的纳米碳纤维， 目前以空心的单壁纳米碳管作为增强相的复合材料力学性能的研究相对较少. Preeti Joshi[10]等利用有限元法计算了多壁碳纳米管增强复合材料的有效弹性模量， 证明多壁碳纳米管在受压情况下能取得较好的有效弹性模量， Shweta Paunikar和Surendra Kumar[11]基于连续介质力学与多相复合材料的微观力学理论模型和能量法则， 计算了长短弯曲型纳米碳管增强复合材料两种情况的有效弹性常数， 证明纳米碳管的弯曲程度会使纳米碳管增强复合材料的纵向弹性模量降低， 横向弹性模量增加， 且对较短的纳米碳管影响更显著. 本文以直线型和弯曲型的实心纳米纤维和空心纳米碳管增强陶瓷基复合材料为研究对象， 利用精确周期性边界条件的均质化法计算复合材料的有效弹性模量， 分析纳米碳管的直径、 长度、 弯曲特性、 各向异性等特征参数的变化对纳米碳管增强复合材料有效力学性能的影响.

1 三维有限元模型的构建

首先对所建模型做以下基本假设： ① 纳米碳管完全分散在陶瓷基体中； ② 纳米碳管规则排列且取向一致； ③ 纳米碳管和基体的界面结合完美,不考虑界面的滑移和脱粘等损伤； ④ 对直线型和余弦波型实心纳米纤维和空心纳米碳管增强复合材料， 只考虑复合材料的弹性性能， 不考虑塑性性能及残余热应力的影响.

利用ANSYS有限元软件建模分析， 采用三维实体结构八节点SOLID45单元， 建立纳米碳管为直线型空心模型， 如图 1(a) 所示； 采用SOLID185单元建立纳米碳管为余弦波型空心模型， 如图 1(b) 所示. 计算时取全模型进行模拟. 陶瓷基体的长度为L， 横截面是边长为t的正方形， 纳米碳管的长度为l， 纳米碳管的外径为d. 主要材料参数参照文献[12]： 纳米碳管的弹性模量Ef=700 GPa， 泊松比vf=0.23； 陶瓷基体的弹性模量Em=402 GPa， 泊松比vm=0.23.

图 1 特征体积单元有限元网格图Fig.1 FEM mesh of RVE

2 精确周期性边界条件的均质化法

[7]所述的多尺度均质化法， 假设图 2 所示为具有周期性微结构的线弹性体，Ω为线弹性体的三维宏观部分，Γ为Ω的边界，Y为周期性胞元，SY为Y的边界.

考虑摄动参数η， 宏观体的位移可表示为

式中：x=(x1,x2,x3)代表宏观坐标系，y=(y1,y2,y3)代表微观坐标系， 其关系可由摄动参数表示为

一般的均质化法假设

Y.

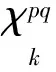
Y.

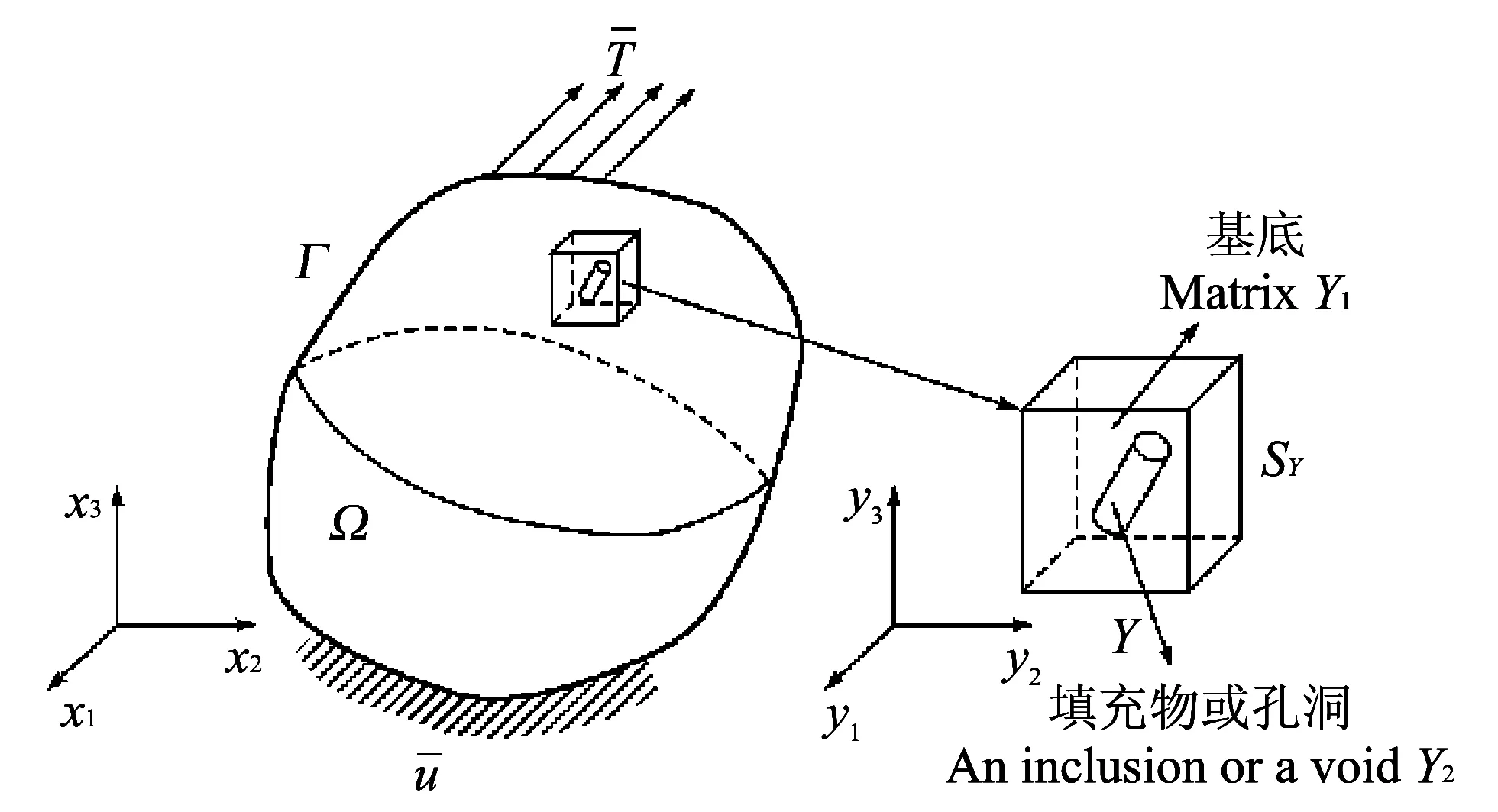
图 2 宏微观坐标Fig.2 Macro-microscopic coordinates

为了提高求解效率， 文献[9]通过假设一个新的特征函数张量将方程(5)转化为齐次方程

式中：δij为Kronecker函数

给定k(k=1,2,3)和pq(p,q=1,2,3)， 将式(7)代入式(5)， 简化后得到的齐次方程为

因此， 根据式(4)和(10)可得到均质化弹性常数为

Y.

根据图 3 所示的一般特征体积胞元， 周期性边界条件可以简化为式(11)所示的3个拉伸和3个剪切和6个简单变形.

图 3 含任意周期性纤维的长方体胞元Fig.3 A rectangular parallelepiped unit cell

|face3=-a,

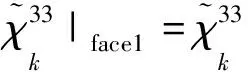
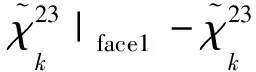
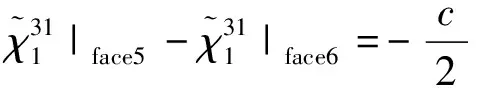
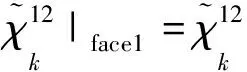
不考虑外力作用的影响， 仅在周期性边界条件(11)作用下， 运用有限元方法求方程(9)的解， 进而利用式(10)求出复合材料的有效弹性模量， 该方法适用于任何形状的特征体积单元.

3 有限元计算结果和讨论

在ANSYS平台构建直线型和弯曲型实心和空心纳米碳管增强陶瓷基复合材料的有限元模型， 利用第2节描述的具有精确周期性边界条件的均质化法， 结合自编FORTRAN后处理程序预测复合材料的有效力学性能.

3.1 纳米碳管的直径对复合材料有效力学性能的影响

首先分析直线型和弯曲型纳米碳管直径对陶瓷基复合材料有效力学性能的影响. 为检验用实心纳米碳管代替空心纳米碳管的可靠性， 同时计算了直线型实心纳米碳管的有效力学性能. 假设基体与纳米碳管均为各向同性材料， 基体长度为150 nm， 宽为30 nm， 纳米碳管长度为120 nm， 空心纳米碳管的壁厚取1 nm， 外径分别取8,12,16,20,24 nm， 其它材料参数不变.

图 4～图 7 是各有效弹性模量在不同纳米碳管直径变化情况下的分布规律.

图 4 不同形状时纵向弹性模量与纳米碳管外径的关系Fig.4 Relationship between longitudinal Young’s mdulus and outside diameter of carbon nanotubes for different shapes

图 4～图 7 结果表明， 对于空心纳米碳管， 随着纳米碳管外径的增大， 直线型和弯曲型复合材料的有效模量均呈减小的趋势， 纳米碳管的形状变化对纵向弹性模量的影响非常小， 对横向弹性模量的影响较明显， 在相同直径情况下， 弯曲型空心纳米碳管增强复合材料的横向弹性模量比直线型纳米碳管略大一些， 剪切弹性模量比直线型纳米碳管小， 由此推断纳米碳管的弯曲程度基本不会降低纳米碳管复合材料的有效刚度. 但对图中所示实心纳米碳管而言， 所有的有效模量变化趋势正好与空心情况相反， 随着纳米碳管直径的增大， 纵横向有效弹性模量和有效剪切模量均呈非线性增大趋势， 而有效泊松比则保持基本保持常数. 主要原因在于纳米碳管的空心结构削弱了它的承载能力， 降低了它作为增强相的增强效果， 因而复合材料的有效刚度呈递减趋势， 可见， 简单地用实心纳米碳管代替空心纳米碳管是不可行的.

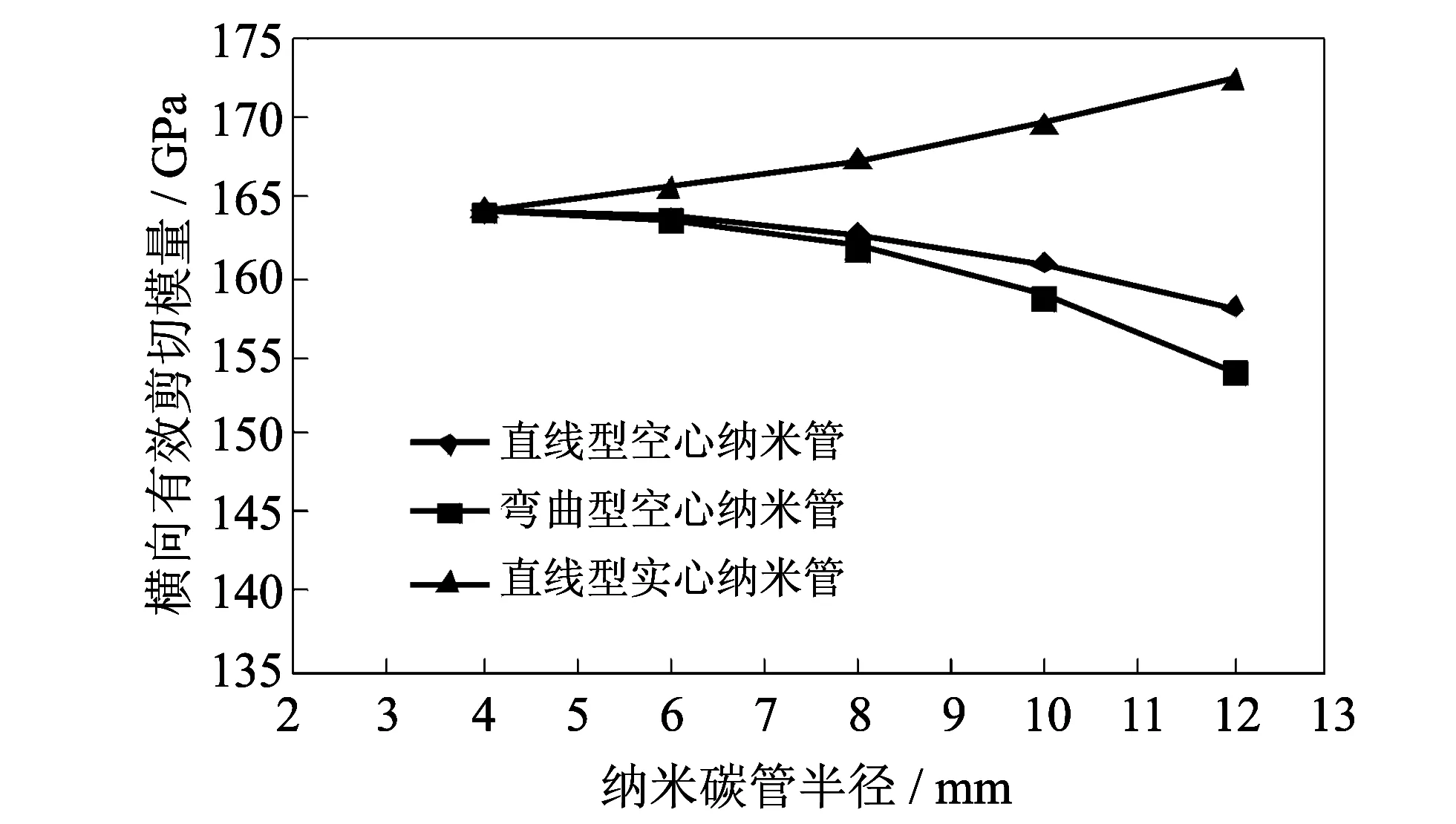
图 5 不同形状时横向弹性模量与纳米碳管外径的关系Fig.5 Relationship between transverse Young’s modulus and outside diameter of carbon nanotubes for different shapes

图 6 不同形状时纵向剪切模量与纳米碳管外径的关系Fig.6 Relationship between longitudinal shear modulus and outside diameter of carbon nanotubes for different shapes

图 7 不同形状时泊松比与纳米碳管外径的关系Fig.7 Relationship between Poisson’s ratio and outside diameter of carbon nanotubes for different shapes

由图 7 还可以看出， 空心情况下， 直线型纳米碳管增强复合材料的泊松比随着纳米碳管外径的增大而显著增大， 具有明显的泊松效应； 对于弯曲型纳米碳管来说， 复合材料的泊松比随着纳米碳管外径的增大而减小， 纳米碳管的弯曲特性有利于减小横向变形. 与空心情况相比， 实心纳米碳管的密实特性对横向变形具有限制作用， 因而泊松比几乎保持常数不变， 显然， 实心纳米碳管会高估复合材料的横向刚度.

3.2 纳米碳管的材料性质对复合材料有效力学性能的影响

考虑到纳米碳管材料的非均匀性， 本文将纳米碳管按照各向同性和各向异性两种材料情况进行分析. 仍然将纳米碳管分为直线型和弯曲型两种类型， 基体视为各向同性材料， 基体的弹性模量Em=402 GPa， 泊松比vm=0.23； 纳米碳管设为各向异性， 其弹性常数分别取为[7]：C11=457.6 GPa，C12=C13=8.4 GPa，C22=C33=14.3 GPa，C23=5.5 GPa，C44=C66=27.0 GPa，C55=4.4 GPa， 泊松比vf=0.42， 空心纳米碳管长度为120 nm， 壁厚为1 nm， 外径分别取8,12,16， 20， 24 nm， 其它材料参数不变. 计算所得各有效弹性模量与纳米碳管外径的关系如图 8～图 11 所示.

图 8 不同材料性质时纵向弹性模量与纳米碳管外径的关系Fig.8 Relationship between longitudinal Young’s modulus and outside diameter of carbon nanotubes for different material properties

由图8～图10可以看出， 随着纳米碳管外径的增大， 复合材料的有效弹性模量和剪切模量仍然呈递减趋势， 与纳米碳管为各向同性所得结果的变化规律基本保持一致， 但各向异性纳米碳管会导致有效弹性模量下降速度更快， 由此可见， 忽略纳米碳管的各向异性会导致过高估计复合材料的有效刚度.

图 9 不同材料性质时横向弹性模量与纳米碳管外径的关系Fig.9 Relationship between transverse Young’s modulus and outside diameter of carbon nanotubes for different material properties

图 10 不同材料性质时纵向剪切模量与纳米碳管外径的关系Fig.10 Relationship between longitudinal shear modulus and outside diameter of carbon nanotubes for different material properties

图 11 不同材料性质时泊松比与纳米碳管外径的关系Fig.11 Relationship between Poisson’s ratio and outside diameter of carbon nanotubes for different material properties

由图 11 的结果可以看出， 当纳米碳管为各向异性材料时， 无论是直线型还是弯曲型纳米碳管增强复合材料的泊松比变化规律基本一致， 但数值上均比纳米碳管为各向同性时大很多， 纳米碳管的各向异性增大复合材料的泊松比， 会使横向变形增大. 纳米碳管为弯曲型时， 泊松比随纳米碳管外径的增大略呈减小趋势， 纳米碳管为直线型时， 泊松比随着纳米碳管外径的增大而缓慢增大， 纳米碳管的弯曲有利于减小泊松效应.

3.3 纳米碳管的长度对复合材料有效力学性能的影响

本节通过改变纳米碳管的长度来研究其对复合材料有效力学性能的影响. 纳米碳管外径6 nm， 壁厚为1 nm， 长度取30, 60, 90, 120, 150 nm. 其它材料参数不变. 复合材料的有效力学性能随直径变化的变化曲线如图 12～图 15 所示.

图 12 不同形状时纵向弹性模量与纳米碳管长度的关系Fig.12 Relationship between longitudinal Young’s modulus and outside diameter of carbon nanotubes for different shapes

图 13 不同形状时横向弹性模量与纳米碳管长度的关系Fig.13 Relationship between transverse Young’s modulus and outside diameter of carbon nanotubes for different shapes

由图12～图14的结果可以看出， 随着纳米碳管长度的增大， 空心纳米碳管增强复合材料的纵向弹性模量均随纳米碳管长度的增大而减小， 弯曲型纳米碳管情况的纵向弹性模量比直线型要大， 说明纳米碳管的弯曲不会降低纵向弹性模量的大小； 横向有效弹性模量与有效剪切模量随纳米碳管的增大缓慢增加， 弯曲型纳米碳管增强复合材料的增大趋势稍弱于直线型情况，弹性模量较直线型的要小，可见，纳米碳管的弯曲程度会影响横向有效弹性模量和有效剪切模量. 由图15可知，随着纳米碳管长度的增大，实心纳米碳管复合材料的泊松比的变化趋势最为平稳， 几乎不随长度改变， 弯曲型纳米碳管复合材料的泊松比缓慢减小， 最显著的变化是直线型空心纳米碳管的泊松比随纳米碳管长度的增大线性增加， 这意味着随着纳米碳管长度的增加， 空心范围扩大， 削弱了复合材料抵抗横向变形的能力， 利用实心纳米碳管代替空心纳米碳管无法体现这种效应， 而纳米碳管的弯曲特性可能能够有效缓解泊松效应.

图 14 不同形状时纵向剪切模量与纳米碳管长度的关系Fig.14 Relationship between effective shear modulus and outside diameter of carbon nanotubes for different shapes

图 15 不同形状时泊松比与纳米碳管长度的关系Fig.15 Relationship between Poisson’s ratio and outside diameter of carbon nanotubes for different shapes

4 结 论

通过ANSYS平台构建三维纳米碳管增强复合材料模型， 利用双尺度均质化理论计算直线型和弯曲型的实心与空心纳米碳管增强陶瓷基复合材料的有效力学性能. 得到如下主要结论：

1) 实心直线型纳米碳管增强复合材料的有效泊松比为常数， 基本不体现材料的泊松效应， 而有效弹性模量和剪切模量随纳米碳管长度和外径的增加均高于空心纳米碳管情况， 且呈完全相反的变化趋势， 证明复合材料的有效刚度受增强相形状的影响较为显著， 实心纳米碳管与空心纳米碳管作为增强相具有不可替代性.

2) 随着纳米碳管长度和直径的变化，直线型和弯曲型空心纳米碳管增强复合材料的纵向有效弹性模量和有效泊松比变化幅度不大，纳米碳管的弯曲程度主要降低横向有效模量和有效剪切模量.

3) 各向异性纳米碳管增强复合材料的有效力学性能明显低于各向同性纳米碳管增强复合材料情况， 用各向同性纳米碳管代替各向异性纳米碳管会过高估计复合材料的有效力学性能.

参考文献:

[1]袁红， 钱江， 王秀喜， 等. 金属基纳米复合材料等效弹性模量的均匀化方法数值模拟[J]. 力学季刊， 2003， 24(4)： 567-571. Yuan Hong， Qian Jiang, Wang Xiuxi, et al. Numerical simulation of equivalent elastic modulus for metal matrix nano-composite materials using homogenization method[J]. Chinese Quarterly of Mechanics, 2003, 24(4)： 567-571. (in Chinese)

[2]吴振江， 黄新民， 於国良， 等. 纳米碳管铝基复合材料组织与性能的研究[J]. 上海有色金属, 2014, 35(3)： 93-99. Wu Zhenjiang, Huang Xinmin, Yu Guoliang, et al. Study on microstructure and properties of aluminum matrix composites reinforced by carbon nanotubes[J]. Shanghai Nonferrous Metals, 2014, 35(3)： 93-99. (in Chinese)

[3]Ashrafi B, Hubert P. Modeling the elastic proper ties of carbon nano-tube array/polymer composites[J]. Composites Science and Technology, 2006, 66： 387-396.

[4]Mori T, Tanaka K. Average stress in matrix and average energy of materials with misfitting inclusion[J]. Acta Metall, 1973, 21： 571- 574.

[5]Shao L H, Luo R Y, Bai S L, et al. Prediction of effective moduli of carbon nanotube-reinforced composites with waviness and debonding[J]. Composite Structures, 2009, 87： 274-281.

[6]Li Ming, Kang Zhan, Yang Peiying, et al. Molecular dynamics study on buckling of single-wall carbon nano-tube-based intra-molecular junctions and influence factors[J]. Computational Materials Science, 2013, 67： 390-396.

[7]Luo D M, Wang W X, Takao Y. Application of homogenization method on the evaluation and analysis of the effective stiffness for non-continuous carbon nanotube/polymer composites[J]. Polymer Composites, 2007, 9： 688-695.

[8]Oliveira J A, Pinho-da-Cruz J, Teixeira-Dias F. Asymptotic homogenization in linear elasticity. Part II： Finite element procedures and multiscale applications[J]. Computational Materials Science, 2009, 45： 1081-1096.

[9]罗冬梅, 汪文学, 高雄善裕, 等. 确定均质化法中精确周期性边界条件的新解法及其在复合材料刚度预测中的应用[J]. 机械强度, 2006, 28(4)： 517- 523. Luo Dongmei, Wang Wenxue, Yoshihiro Takao, et al. New method to determine the exact periodic boundary conditions for Macro-microscopic homogenization analysis and its application on the prediction of effective elastic constants of periodic materials[J]. Journal of Mechanical Strength, 2006,28(4)： 517-523. (in Chinese)

[10]Joshi P, Upadhyay S H. Evaluation of elastic properties of multi walled carbon nanotube reinforced composite[J]. Computational Materials Science, 2014, 81： 332-338.

[11]Paunikar S, Kumar S. Effect of CNT waviness on the effective mechanical properties of long and short CNT reinforced composites[J]. Computational Materials Science, 2014, 95： 21-28.

[12]浦毅杰, 纳米陶瓷基复合材料有效热-力学性能的有限元分析[D]. 广州： 华南理工大学, 2015.

Influence of the Characteristic of Lined and Waved Nano-Tube on Effective Mechanical Properties of Nano-Composites

SONG Rui-lan, LUO Dong-mei, XIE Yue, SU Xiao-ru

(Dept. of Civil Engineering, Foshan University, Foshan 528000, China)

The model of three dimensional representative volume element for ceramic matrix composites reinforced by the lined and waved nano-tube with solid and tubular cylinder was constituted on the ANSYS platform. The double scale asymptotic homogenization theory was used to calculate the effective mechanical properties of ceramic composites with nano-tube, and the influence of the geometrical shape and mechanical characteristic of nano-tube on effective stiffness of nano composites was analyzed. The result shows that the difference between the effective stiffness of nano composites reinforced with solid and tubular nano-tube is obvious and non-substitutable. Moreover, the anisotropy of the nanotube decreases the effective stiffness of nano-composites, and the effective stiffness is over-estimated when the nanotube is taken as the isotropic material. The transverse effective stiffness and shear stiffness of nano-composites are influenced obviously by the waved nano-tube. It is significant to predict the effective stiffness accurately by constituting a correct three dimensional model, and selecting the nano-tube with reasonable shape and size.

nano-tube；nano-composites；effective elastic constants；two-scale homogenization method

1673-3193(2016)06-0659-07

2015-12-11

国家自然科学基金资助项目(10772047/A020206,11172066/A020305)； 广东省自然科学基金资助项目(S2011010004874)

宋瑞兰(1987-)， 女， 硕士， 主要从事土木工程的研究.

罗冬梅(1965-)， 女， 教授， 博士， 主要从事纳微米复合材料的力学性能研究.

O345

A

10.3969/j.issn.1673-3193.2016.06.018