从确定的数到抽象的字母

田载今

人们为什么要用字母表示数？什么是整式？数的运算和整式的运算有哪些相似之处？请大家认真听田老师讲一讲吧。

数的产生既来源于实际生产和生活的需要，又来源于研究数学问题的需要，例如，为区别收入1元和支出1元，可以将它们分别记为1元和-1元，而有了-1，像1-2这类“小减大”的数学问题也得以解决。

每个数都是一个具体确定的值，由数组成的算式的运算结果也是确定的值，例如，1+2表示l和2这两个大小确定的值相加，所得结果3也是一个确定的值，正因为数具有确定性，所以人们研究确定的量时离不开数，

数的确定性虽然使数能精确地表示量的大小，但是又使数的使用受到限制，研究一股性问题时，只有具体的数就不够了，例如，要用式子表示加法交换律，就不能用l+2：2+l，也不能用2+3=3+2，因为这样的式子都只能表示“某两个具体的数相加时，交换加数的位置，和不变”，而加法交换律是一般运算律，它适用于任意两个加数，不能用某两个具体的数来表示，研究含有未知数的数量关系时，同样不能只用具体的数，例如，要用式子表示“某个数的3倍比另一个数的2倍大1”，就要注意这里的“某个数”和“”一个数”都是未知数，虽然用具体的数可列出3×5=2x7+l，3x7=2x10+1，3x9=2x13+1等一系列式子，但是满足这一数量关系的“某个数”和“另一个数”有无穷多组，用有限多个式子无法完全表示它们。

随着数学的发展，人们越来越关注一般性问题，含有未知数的数量关系成为人们经常研究的内容，这促使数学语言也要与时俱进，突破只能使用具体的数的限制，为此，人们逐渐想到用抽象的符号代替具体的数，而字母就是一种使用起来很方便的符号，例如，用式子a+b=6+a表示加法交换律，这里的字母a和b没有确定的值，它们可以表示任意两个数，于是这个式子就有了一般性，义如，用式子3x=2y+1表示“某个数的3倍比另一个数的2倍大l”，这里的字母x和y没有确定的值，它们可以表示满足这一关系的任意两个数，包括“x=5，y=7”“x=7，y=10”“x=9 y=13”等无穷多种情形。

代数学是数学的一个重要分支，清代学者华蘅芳在他和英国人傅兰雅合译的西方数学著作《代数学》的卷首写道：“代数之法，无论何数，皆可以任何记号代之，”这显示出代数的基本方法起源于用符号表乐数，

1591年，法国数学家韦达（1540-1603）最先在数学著作中系统地用字母表示数，韦达认为：用字母表示数，可使一般性问题成为研究对象，让数学从传统的侧重于数的运算的算术中得到发展，韦达的创举促进了代数学的诞生，因此他被后人称为“代数学之父”。

有了用字母表示数的创举，式子中便可以出现字母（字母还可以表示未知数），这样的式子更适合用来研究一般性问题，所以这种由数与字母组成的式子成为代数研究的基本内容。

人教版初中数学教科书的第二章是“整式的加减”，整式是一种最简单的代数式，加减法是最基本的整式运算，运算的主要方法是合并同类项，这一章是代数式内容的入门章，也是大家后续学习的重要基础。

在代数式中，字母的地位比数要高，式子的分类，一般以其中字母的情况为标准，例如，区分整式与分式的方法是看分母中是否含有字母，整式中可以有分母，但分母中不能有字母，例如，a/2的分母中没有字母，它属于整式：2/a的分母中有字母，它不属于整式，

因为整式中的字母是用来表示数的，所以它们可以像数一样进行运算，数的运算法则和规律对整式的运算仍然适用，整式也有加减乘除四则运算，人教版教科书中分两次安排了这些内容，第二章只讨论整式的加减运算，乘除运算到八年级再讨论，通过第一章的学习，我们已经知道，在有理数的运算中，减法可以转化为加法，减去数a就等于加上它的相反数-a，这样加减法就可以统一了，因此，整式的加减法也可以统一起来认识，都看作求代数和的加法。

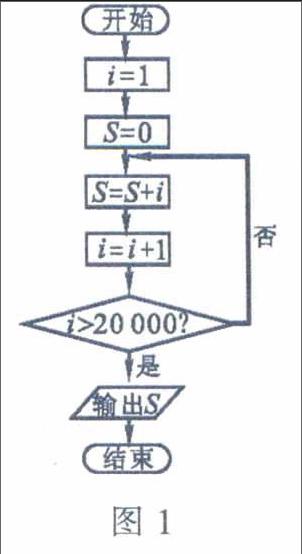
电子计算机的发明是20世纪人类最伟大的成就之一，在它的发明和应用过程中，用字母表示数的方法发挥了重要作用，下面是一个简单的例子：要给计算机编制一个程序，求l+2+3+…+19999+20000的和，图1是对应的程序框图，这是一个循环结构的计算过程，其中的字母i表示一个取值从1开始，逐次加1，直至20001为止的变量：字母S表示随着加数不断增加而逐渐增大的和，计算机开始运行程序后，字母i作为加数按1，2，3，…，20000的顺序逐次加到5中：字母5作为和按O，0+l，0+l+2，0+1+2+3，…，0+1+2+3+…+19999+20000的顺序增大，当i=20 001时，计算结束，输出最终结果200010000，可以看出。字母i和S在程序中有非常重要的作用。

从确定的数到抽象的字母，研究对象的发展是数学前进的一座里程碑，正如数学家华罗庚所说：“数学的特点是抽象，正因如此，用符号表示数就更具有优越性和广泛的应用性。”