应用双谱分析和分形维数的雷达欺骗干扰识别

杨少奇,田波,周瑞钊

(空军工程大学防空反导学院,710051,西安)



应用双谱分析和分形维数的雷达欺骗干扰识别

杨少奇,田波,周瑞钊

(空军工程大学防空反导学院,710051,西安)

为解决频谱弥散干扰(SMSP)和切片组合干扰(C&I)2种干扰类型的识别问题,提出了一种利用双谱分析和分形维数的干扰识别方法。首先对零中频处理后雷达接收信号进行双谱分析,得到接收信号的三维双谱信息;然后通过降维方法把三维信息变换成二维特征曲线,以减小干扰识别的计算量;最后提取二维曲线的盒维数和信息维数2个特征参数,通过支持向量机对干扰识别率进行检验。仿真结果表明:在一定的噪声背景下,该识别方法能够较为稳定地识别不同干扰形式;在信噪比为0 dB的条件下,干扰的识别成功率能够达到88%以上,证明了干扰识别方法的有效性。

雷达;双谱分析;分形维数;欺骗干扰;信号识别

现代化局部战争的一个显著特点就是信息化,雷达作为信息化战争中的重要组成部分,对抗性异常激烈,其中综合干扰技术更是与之相生相克。随着欺骗干扰技术的发展,干扰信号与雷达目标回波信号特征接近,传统的基于能量的雷达目标检测方法难以分辨目标真假,对雷达检测性能造成重大影响[1]。文献[2-3]提出了雷达智能化对抗欺骗干扰的基本模式,认为雷达对抗干扰的核心是识别跟踪系统是否受到干扰以及受到的干扰类型,进而采取相应的干扰抑制措施。

频谱弥散干扰(smeared spectrum,SMSP)和切片组合干扰(chopping and interleaving,C&I)是针对线性调频脉冲压缩雷达的2种干扰[4],能够在雷达接收端同时产生大量假目标,给雷达探测和跟踪目标带来严重干扰。文献[5]利用匹配信号变换估计SMSP干扰的调频斜率,根据干扰信号和目标回波调频斜率的不同对SMSP干扰信号进行识别;文献[6]分析了组网雷达系统中SMSP干扰的特点,同样根据干扰与目标调频斜率的不同,利用分数阶域功率谱和恒虚警检测对雷达中SMSP干扰进行了存在性检测。但是,总体看来对此类干扰识别的研究较少,且只针对单一的SMSP干扰,而未涉及C&I干扰。

高阶谱分析方法能够很好地分析非线性、非高斯信号,并且可以有效地抑制高斯噪声,提取随机过程偏离高斯分布的程度,因此被广泛应用于信号分类识别[7-10]中,但高阶谱分析存在计算量大的问题。一般应用中多采用双谱分析,并利用围线积分、选择双谱等方法降低特征参数的维数和计算量[11-12],但是仍然存在计算量大、冗余项和信息丢失等问题。分形理论主要用于刻画信号空间分布的不规则度和复杂性,广泛应用于图像处理、模式识别和雷达信号识别等领域[13-17]。SMSP与C&I干扰信号作为一种时间序列,与雷达辐射源信号、电台调制信号等类似,分形理论可以刻画其复杂度特征[16-17]。

本文提出了一种将双谱分析与分形维数相结合的SMSP和C&I干扰检测与识别方法。首先对雷达接收信号进行双谱分析,并提取其幅度谱信息,其次通过降维变换得到二维特征曲线,利用分形理论求取特征曲线的盒维数和信息维数,最后通过支持向量机(support vector machines,SVM)实现对雷达接收信号中SMSP和C&I干扰的检测识别。

1 SMSP和C&I干扰原理

SMSP与C&I干扰是针对线性调频脉压雷达的2种欺骗式干扰。SMSP干扰的产生过程为:干扰接收机接收到雷达发射信号后,通过混频、低通滤波、模数转换后将数据存入数字射频存储器(DRFM);然后,将数据送入数据缓冲区,经传输门并行传输到移位寄存器组,其中移位寄存器的时钟频率是控制数据送入DRFM时的时钟频率的N倍;数据重复N次后串行进入数模转换器,经混频滤波由发射机将干扰信号发射出去,干扰信号是由N个子脉冲组成的调频斜率为雷达发射信号N倍的时宽不变的信号。Sparrow等人证明在N=5～7时,可获得最优的干扰效果[4]。设雷达发射信号为线性调频信号,其形式为

St(t)=exp(jπkt2)

(1)

式中:k、B、T分别为发射信号的调频斜率、带宽和脉宽。根据SMSP信号产生原理,将时钟频率调成原频率的N倍,则得到第一个子脉冲信号为

J1(t)=AJexp(jπk′t2)

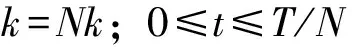
(2)

式中:AJ为干扰信号幅度。将这一子脉冲信号重复N次即得到干扰信号时域表达式如下

(3)

C&I干扰产生的过程为:首先将干扰机接收的雷达信号脉宽T分为宽度相等的若干个时隙(slot),再用一个均匀间隔的矩形脉冲串对存储在DRFM中的雷达发射信号取样,得到与雷达信号波形完全相同的子脉冲串波形,此为Chopping阶段;然后,将这一子脉冲串波形复制到相邻的时隙中,即每一子脉冲都被复制若干次,把与该子脉冲右侧相邻的空时隙都填充满,此为Interleaving阶段。根据C&I干扰产生原理,取出的雷达信号子波形为

(4)

式中:M、N分别为矩形脉冲串的脉冲个数和雷达信号脉宽划分的时隙个数。在Interleaving阶段,将取出的子波形填充到相邻时隙得到完整的时域干扰信号如下

(5)

图1为SMSP和C&I干扰的时域波形与干扰效果图。可以看出2种干扰样式均能在目标前后产生大量密集假目标,给雷达正常探测、跟踪目标带来了巨大的难度,因此需要对干扰进行检测识别,以便采取具有针对性的抗干扰措施。

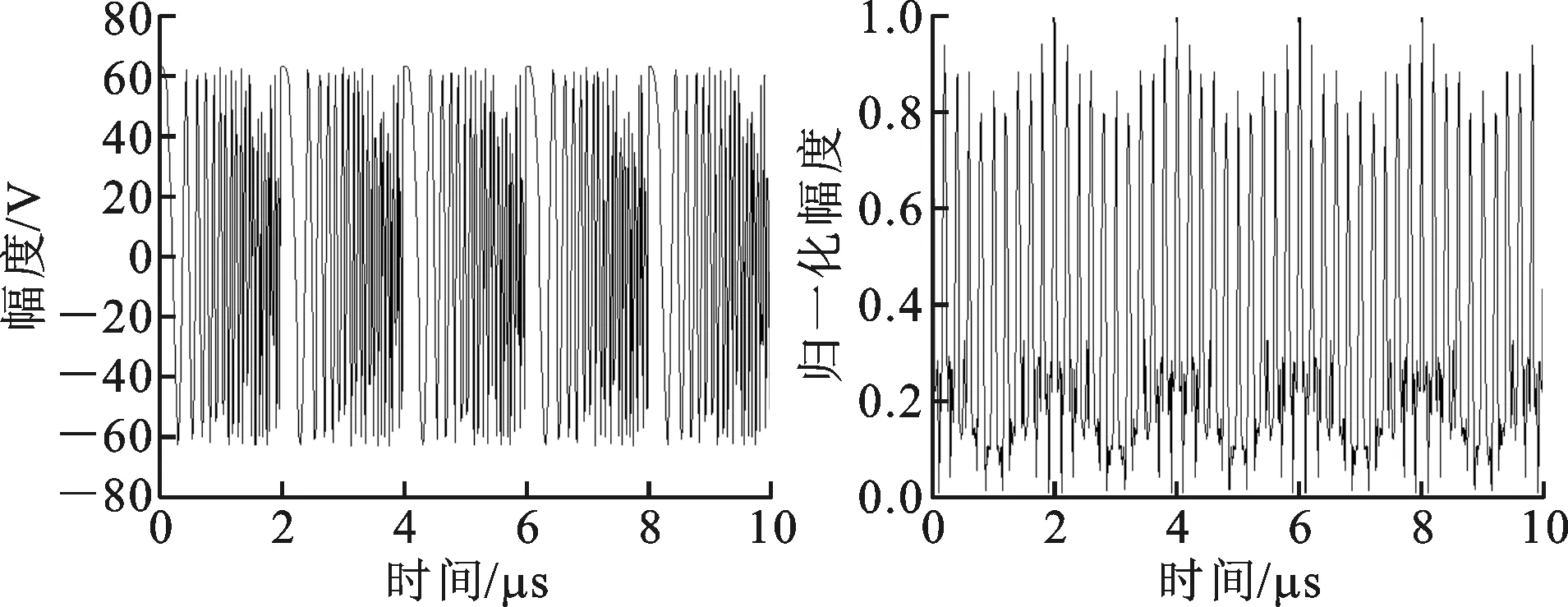
(a)SMSP时域波形 (b)SMSP脉压输出

(c)C&I时域波形 (d)C&I脉压输出图1 SMSP和C&I干扰时域波形与脉压输出

2 干扰特征提取方法

2.1 双谱分析原理

双谱分析属于高阶谱分析的一种,是传统功率谱的推广,应用最为广泛。传统的功率谱分析只适用于线性系统[9],而双谱分析能够检测和刻画信号的非线性特性,并且可以抑制雷达接收信号中的高斯噪声,因此更适用于雷达接收信号的分析。假设{x(i)}为零均值k阶平稳随机过程,并且其k阶累积量Ck,x(τ1,τ2,…,τk-1)是绝对收敛的,即

(6)

则{x(i)}的k阶谱是其k阶累积量离散傅里叶变换

exp{-j2π[ω1,ω2,…,ωk-1][τ1,τ2,…,τk-1]T}

(7)

k阶谱又称为多谱或累积量谱。三阶谱习惯上称为双谱,记作Bx(ω1,ω2),其定义为

(8)

在实际信号处理中,只能根据有限的观测数据得到双谱的估计,本文选用基于非参数法的直接估计方法,该方法的计算量较少,适用于雷达接收信号实时处理的场合。双谱估计的具体步骤如下。

步骤1 将长度为N的观测数据{x(i)}分成K段,每段数据有M个点,即N=KM,也可以重叠分段,即相邻数据有一半重叠,即2N=KM。除去每段数据的均值,将每段数据的均值变为0,如果需要,每段数据可补0,以便于做快速傅里叶变换(FFT)。

步骤2 对第j段数据{xj(i)}做离散傅里叶变换(DFT),并根据DFT系数,分别求出每段数据的双谱估计,即

(9)

(10)

式中:Δ0=fs/N0为频率抽样间隔,fs为数据采样频率,N0为双谱域内ω1与ω2轴的频率采样点数;N0和L1之间应满足M=(2L1+1)N0。

步骤3 根据各段数据双谱估计的结果,进行统计平均,得到观测数据{x(i)}的双谱估计

(11)

式中:ω1=2πfsλ1/N0;ω2=2πfsλ2/N0。

图2为高斯噪声背景下雷达接收信号中分别存在目标回波、目标回波+SMSP干扰、目标回波+C&I干扰时的双谱分析结果,其中信噪比RSN=5 dB。由图2可以看出,3种情况下雷达接收信号的双谱估计具有明显不同的特征,并且能够有效地抑制高斯噪声的影响,因此双谱分析能够提取雷达接收信号中干扰信号的特征。但是,由于直接利用双谱估计结果进行检测识别会带来的大量的计算负担,因此需要进一步的降低特征维数。

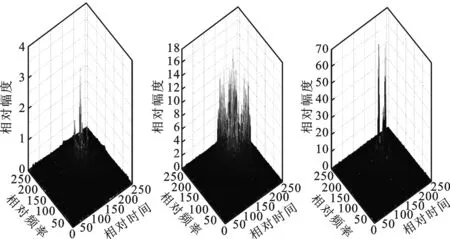
(a)目标回波 (b)目标回波+SMSP (c)目标回波+C&I图2 雷达接收信号双谱估计结果

2.2 分形维数特征提取

雷达接收信号经过双谱分析之后得到一个三维特征谱,由于存在数据量大缺陷不利于实时处理,因此需要对雷达接收信号双谱特征进行降维。在降维过程中要注意两个原则:一是减少计算量,提高运算速度;二是降维之后的特征能够反映不同的干扰样式[8]。根据这两个原则,将得到的三维双谱沿Y轴投影到X轴,即可得到一个在XOZ平面的二维特征序列

(12)

图3分别为目标回波、SMSP干扰存在和C&I干扰存在3种情况下降维后的二维特征谱曲线,其中信噪比RSN=5 dB。由图3可以看出,2种不同干扰样式和只存在目标回波时的雷达接收信号的二维特征谱存在明显的不同,因此能够反映不同类型信号的特征,同时这一降维方法简单,且计算量小。

(a)目标回波 (b)目标回波+SMSP (c)目标回波+C&I图3 雷达接收信号二维特征谱曲线

经过降维后的特征序列仍然存在数据较大的问题,进行特征匹配和模式识别时计算较为复杂,因此需要进一步对二维特征谱提取特征参数。根据图3可以看出,3种情况下的特征谱曲线具有不同的几何分布以及不同的密集程度,因此它们在空间分布上具有不同的复杂度以及不同的密集度。分形维数是分形理论最主要的参数,能够定量描述分形集的复杂性和不规则性[13]。分形理论中的盒维数反映了分形集的几何尺度情况,其最基本的分形维数是Hausdorff维数,但是实际应用中计算起来很复杂,因此通常用盒维数来代替之,通常意义下盒维数约等于Hausdorff维数[13-14]。

下面给出盒维数的一般定义:设(X,d)是一个度量空间,H是X的非空紧集族,ε是一个非负实数,令B(x,ε)表示一个中心在x、半径是ε的闭球。设A是X中的一个非空紧集,对于每个正数ε,令N(A,ε)表示覆盖A的最小闭球数量,即

(13)

式中:x1,x2,…,xM是X不同的点。若存在

(14)

则称Db是集合A的分形盒维数。假设雷达接收信号二维特征序列Rx的长度为N,根据盒维数的定义,将二维特征序列Rx置于单位正方形内,横坐标的最小间隔为q=1/N,则Rx的盒维数可以表示为

Db=-lnN(q)/lnq

(15)

(16)

盒维数仅能反映二维特征谱的几何尺度情况,若想反映其空间分布的疏密程度,需要引入信息维数。设A是Rn的集合,{X(i),i=1,2,…,N}是A的一个有限δ-覆盖,令Pi表示集合A的元素落在集合Xi的概率,其表达式为

(17)

(18)

根据信息维数的定义,二维特征序列Rx的信息维数计算方法如下

(19)

3 仿真分析

3.1 特征参数仿真分析

根据雷达是否受到干扰以及受到干扰的类别,雷达接收信号可以分为以下3种情况

(20)

式中:S0(t)、JSMSP(t)、JC&I(t)、n(t)分别为目标回波信号、SMSP干扰信号、C&I干扰信号和高斯白噪声。本节针对这3种情况对雷达接收信号进行分形盒维数和信息维数的特征提取。仿真参数设置如下:雷达发射信号脉宽为10 μs,带宽为20 MHz,采样频率为60 MHz,SMSP干扰分为5段,C&I干扰分为5段,每段4个时隙。干信比RJS=6 dB,信噪比RSN=0～15 dB,每个信噪比下做600次Monte-Carlo实验,其中前300次实验数据用来分析特征参数变化情况,后300次实验数据用来测试识别率,并且假设干扰信号与目标回波之间没有时间延迟。双谱估计参数设置如下:FFT计算的长度为512个采样点,Rao-Gabr窗口长度为5个采样点,每段数据的采样点为128,每段数据的重叠度为0。仿真结果如图4所示。

(a)盒维数变化曲线

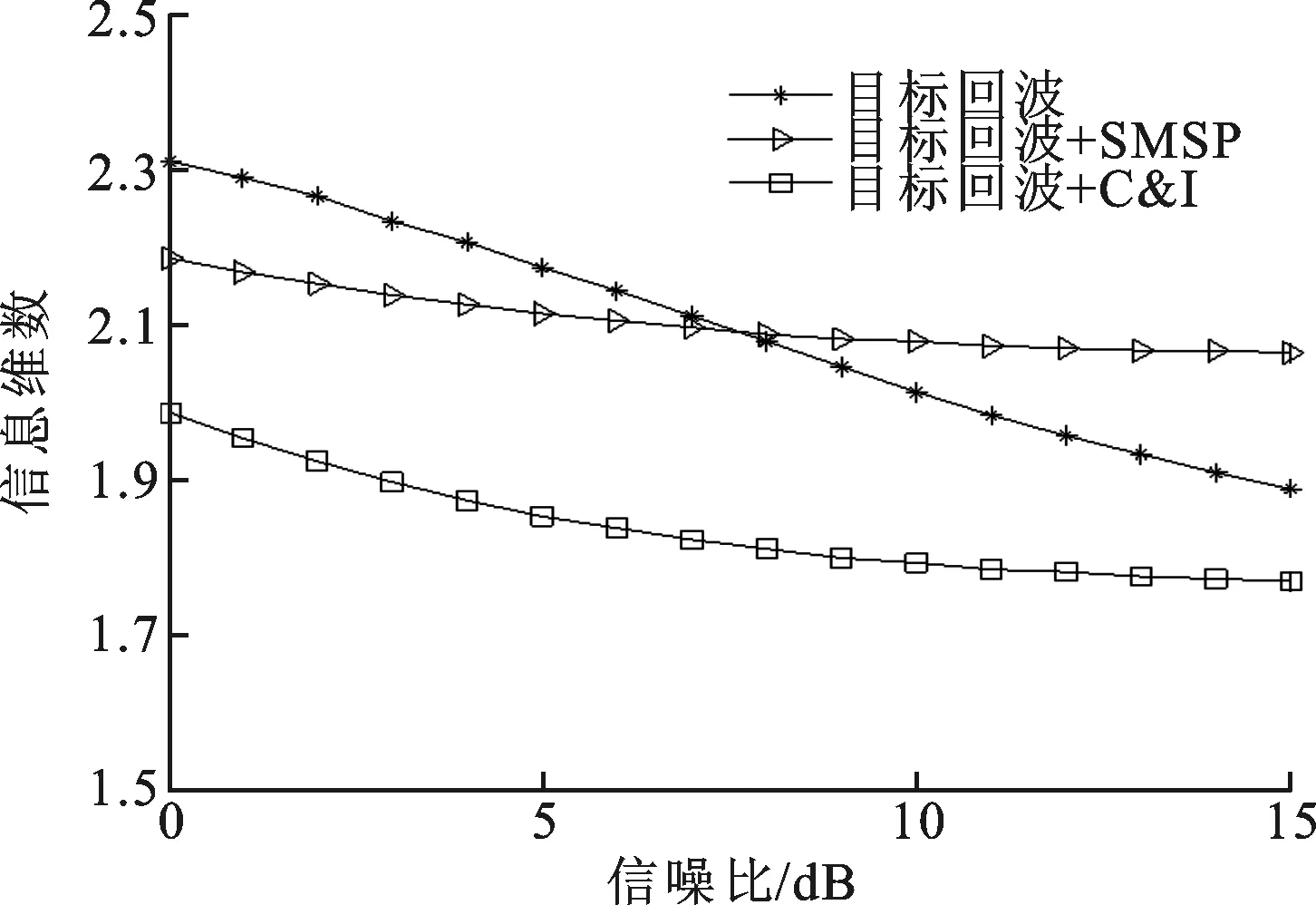
(b)信息维数变化曲线图4 雷达接收信号特征参数变化曲线

根据图4可以看出,雷达接收信号的盒维数特征较为稳定,目标回波的盒维数与SMSP和C&I干扰存在下的盒维数具有明显的差异,但是SMSP和C&I干扰之间的差别较小。同时可以看出,雷达接收信号的信息维数随着信噪比的增大逐渐趋于稳定,目标回波的信息维数变化曲线和SMSP干扰存在交叉,但是SMSP干扰和C&I干扰的信息维数具有明显的差异,这一点正好弥补盒维数的缺点。因此将2个特征参数联合起来用于雷达接收信号中干扰的检测与识别将会起到较好的结果。

3.2 干扰识别与影响因素

根据前文所提取的特征参数,将2个特征参数联合起来组成特征向量,利用一对一多分类支持向量机来识别干扰类型,结果如图5a所示。文献[18]利用模糊函数特征对SMSP和C&I干扰识别进行了研究,识别率如图5b所示。

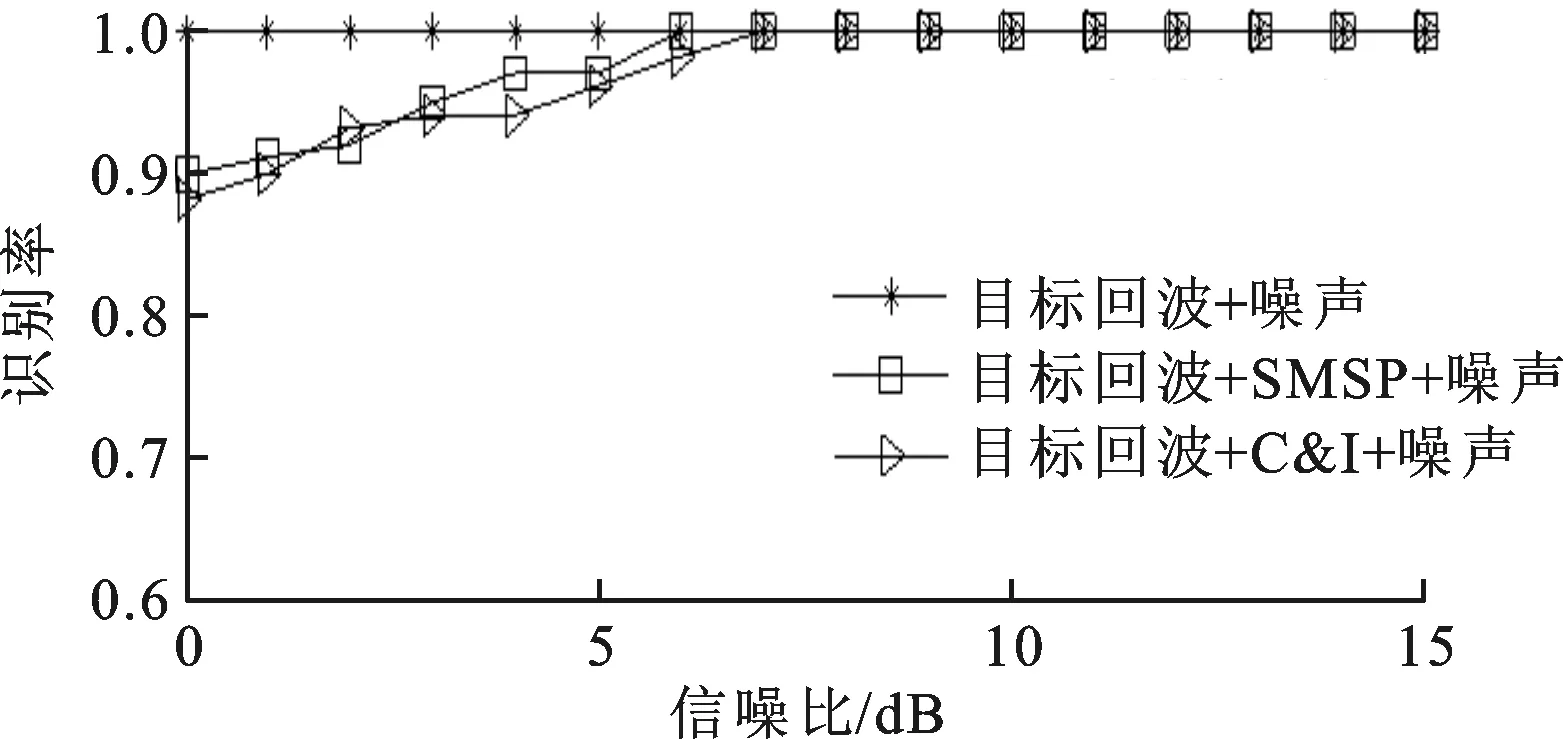
(a)本文方法的识别率曲线

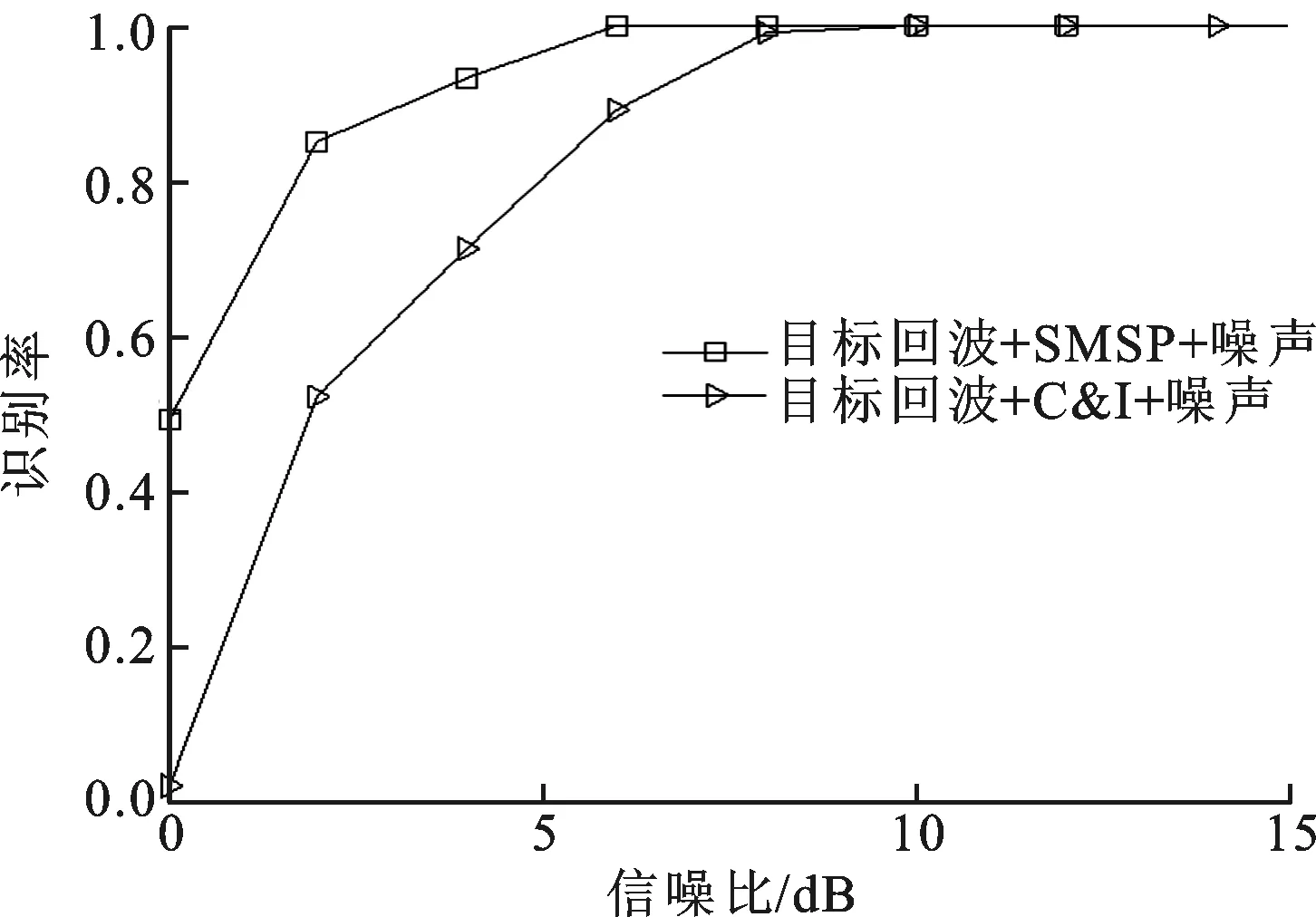
(b)文献[18]方法的识别率曲线图5 2种方法的干扰类型识别率曲线

根据图5a可以看出:雷达接收信号整体识别率较为稳定,在整个信噪比变化范围内均能保持在88%以上,且目标回波的识别率稳定在100%;在RSN=0 dB时,SMSP干扰和C&I干扰的识别率也分别为90%和88%。图5b为RJS=10 dB时文献[18]方法的干扰识别率曲线,根据文献[18]可知,随着干信比的增加,干扰识别率随之增大,虽然图5b中的干信比大于图5a,但在低信噪比下,本文方法的识别率却更高,稳定性更好,因此本文方法的性能优于文献[18]方法。本文方法能够有效地抑制噪声的影响,可以检测出雷达接收信号中是否存在干扰,并且识别出雷达接收信号中存在的干扰类型。

由于干扰类型检测识别成功率受到很多因素的影响,因此需要对主要的影响因素进行分析,包括干噪比变化、干扰信号分段数以及干扰信号存在时延的情况。由于盒维数和信息维数的计算是一个统计过程,难以定量分析,因此下面通过仿真的方法对算法影响因素进行说明。主要仿真所提取特征参数的变化情况,并与3.1节进行对比分析,得到识别成功率的变化趋势,仿真结果如图6～图8所示。

(a)盒维数变化曲线

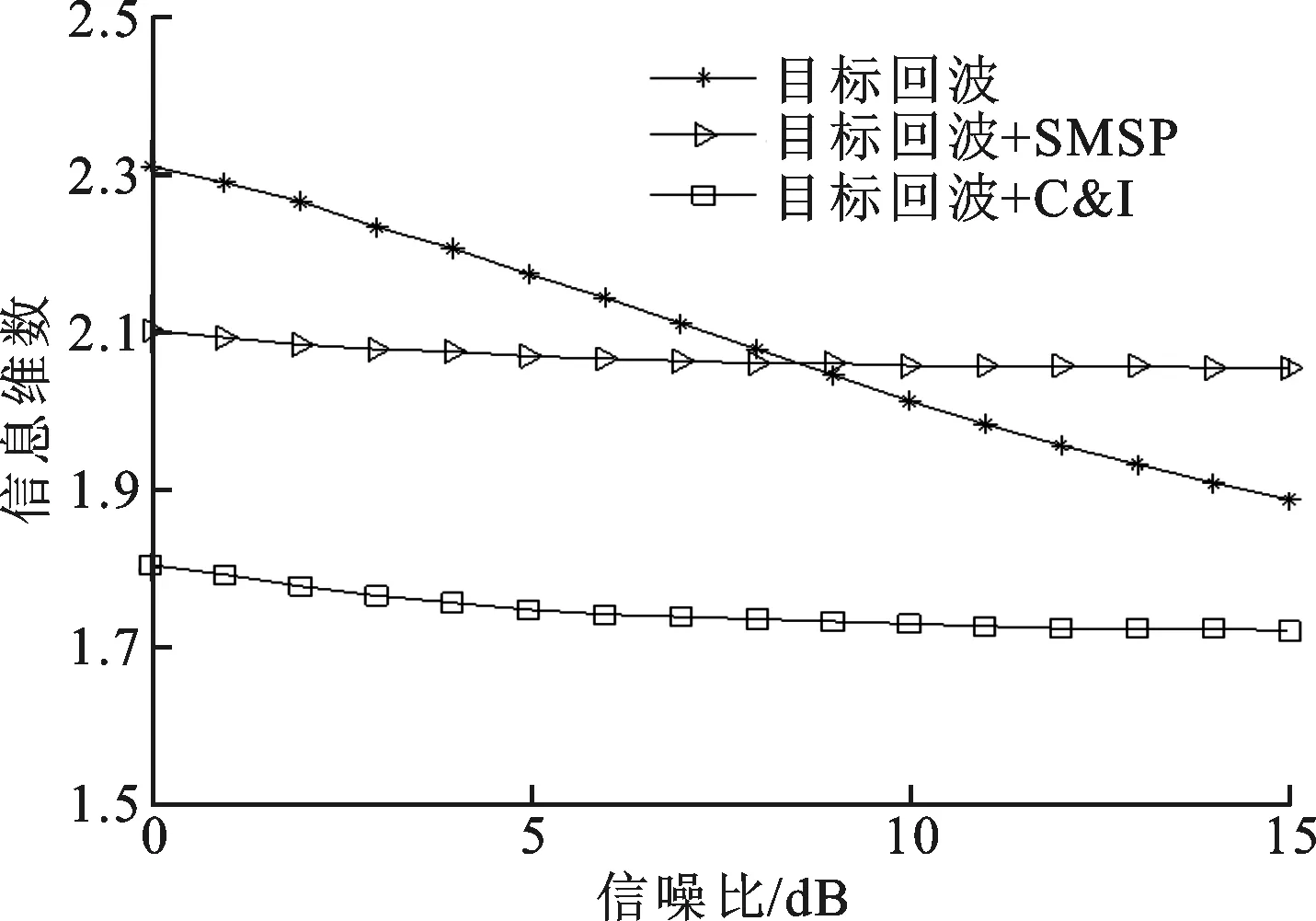
(b)信息维数变化曲线图6 RJS=12 dB时雷达接收信号特征参数变化曲线

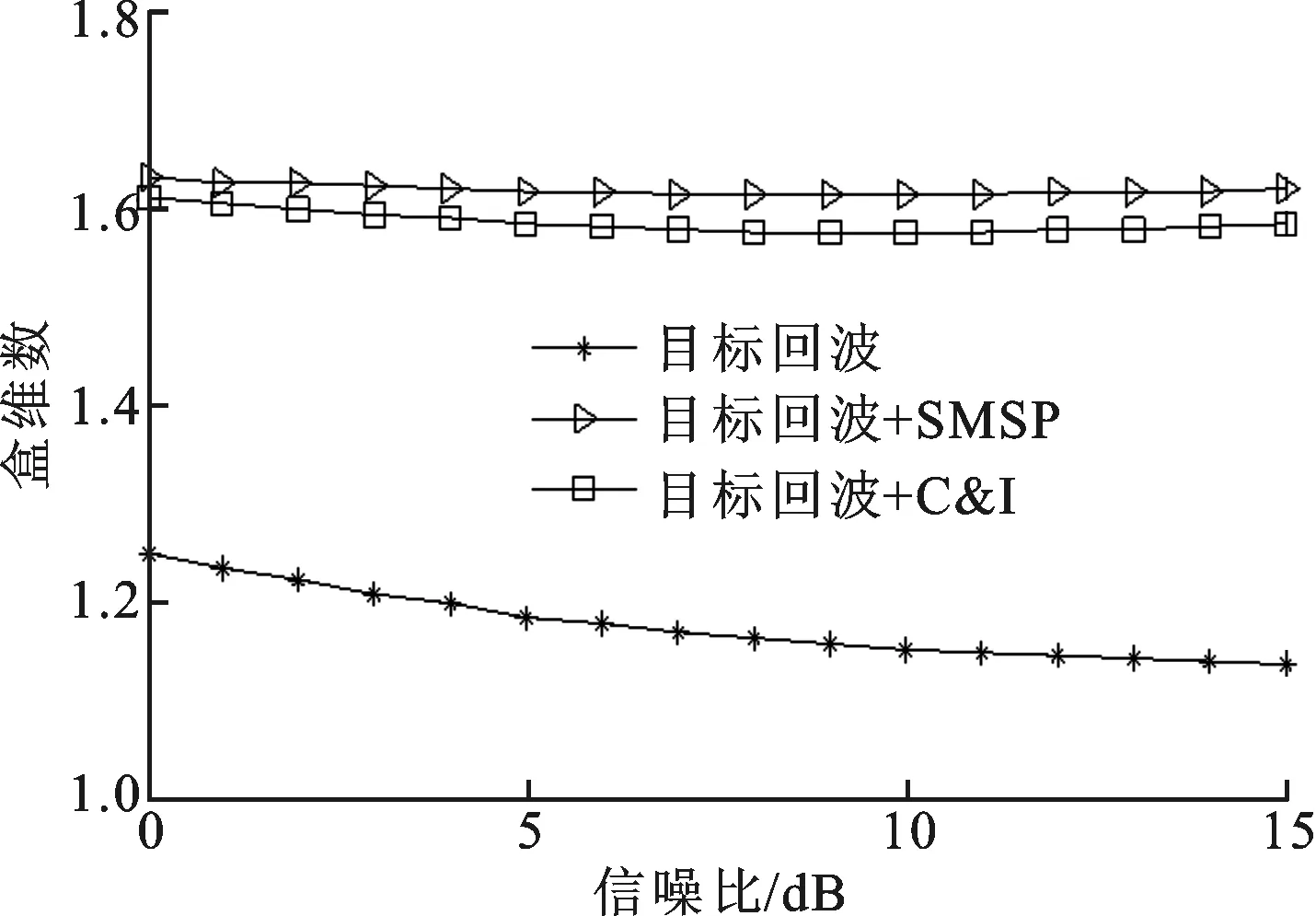
(a)盒维数变化曲线

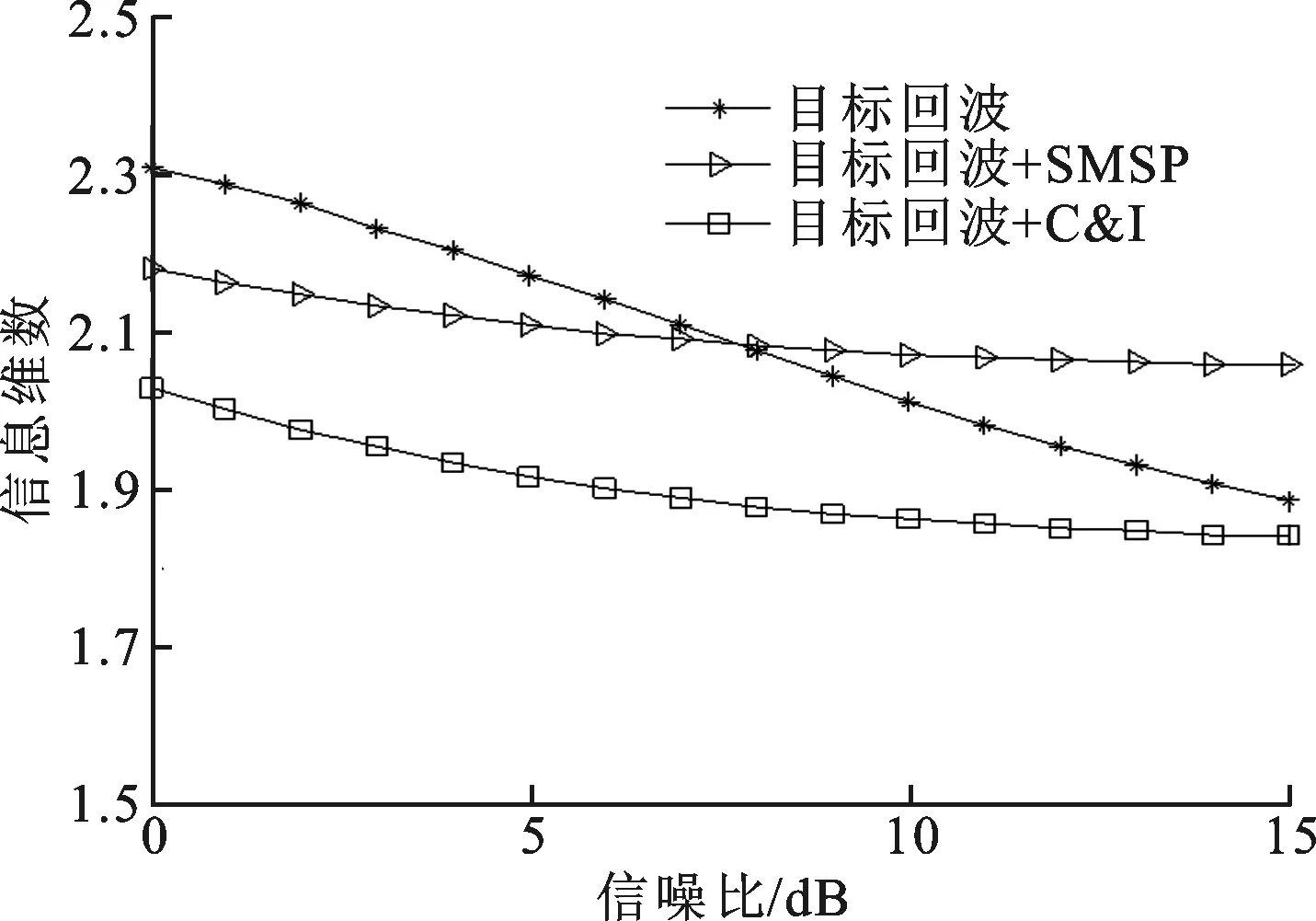
(b)信息维数变化曲线图7 干扰分段为6时雷达接收信号特征参数变化曲线

(a)盒维数变化曲线

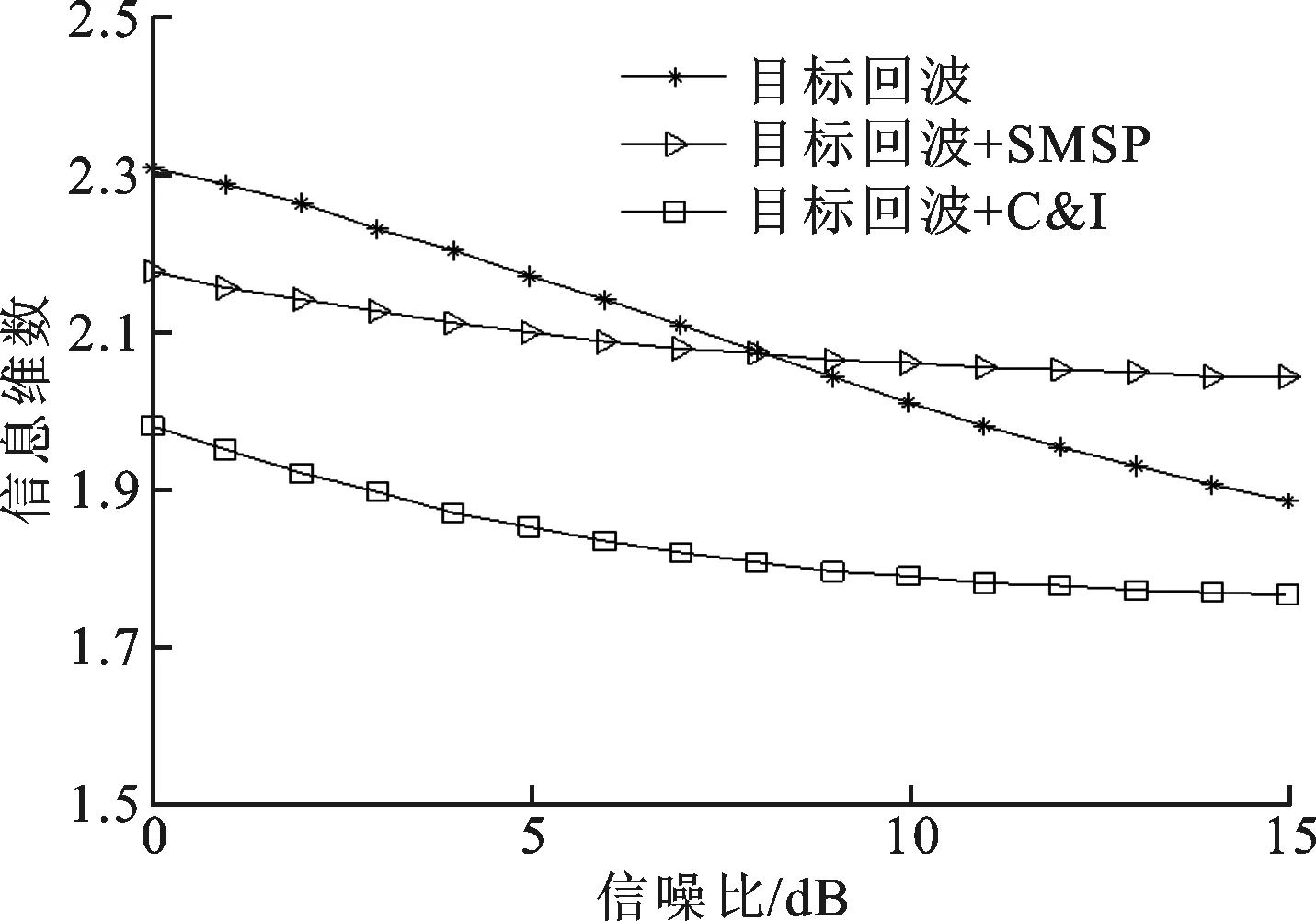
(b)信息维数变化曲线图8 时延为200 ns时雷达接收信号特征参数变化曲线

图6为RJS=12 dB时特征参数随信噪比的变化情况,与图4对比可以看出,盒维数变化不明显,但是SMSP和C&I干扰的信息维数可分离性更大,因此,随着干信比的增加干扰识别成功率也会增大。图7中,SMSP干扰的分段数为6,C&I干扰的分段数为6,每段4个时隙。通过图7与图4的对比可以看出,盒维数的变化不大,信息维数的可分离度有稍微的减小,但是能够区分SMSP和C&I干扰,因此干扰识别成功率会有少许下降。图8中2种干扰信号相对于目标回波均有200 ns的时间延迟,与干扰机的信号处理时延相当。对比图8与图4可以看出,2种特征参数均无明显的变化,因此干扰识别成功率基本不会改变。

雷达欺骗干扰样式复杂多样,为验证本文所提方法的有效性和独有性,现对移频多假目标干扰的特征参数进行仿真分析,并与SMSP和C&I干扰进行对比。移频多假目标干扰为5个移频干扰的合成,其中移频量分别为-2.5、-1.5、0.6、1、3 MHz,RJS=6 dB,其他参数与前文一致。对移频多假目标干扰特征参数进行提取,得到结果如图9所示。

(a)盒维数变化曲线

(b)信息维数变化曲线图9 移频多假目标干扰特征参数变化曲线

将图9与图4进行对比,可以看出,移频多假目标干扰的盒维数参数稳定在1.4附近,与SMSP和C&I干扰均不相交,而信息维数参数在低信噪比下与SMSP和C&I干扰有所交叉,但随着信噪比的增大,逐渐稳定在2.6附近,与二者分离性较好。因此本文所提取的特征参数能够识别多假目标干扰,同时也说明了特征参数的独有性。

4 结 论

本文提出了一种基于双谱分析和分形维数的SMSP和C&I干扰的检测识别方法,通过理论分析和仿真验证,得出如下结论:

(1)基于非参数法的直接双谱估计方法能够有效地抑制高斯噪声,保证了特征参数的稳定性；

(2)对雷达接收信号的三维双谱进行降维后再提取特征参数,降低了识别方法的计算量；

(3)联合2种特征参数并利用支持向量机分类器对干扰信号进行识别,保证了识别成功率；

(4)本文没有考虑多种干扰样式同时进入雷达接收机的情况,以及没有纳入所有常见的欺骗式干扰样式,下一步将对其进行研究。

[1] 闫海, 李国辉, 李建勋. 雷达抗欺骗式干扰信号特征提取方法 [J]. 电子科技大学学报, 2015, 44(1): 50-54. YAN Hai, LI Guohui, LI Jianxun. Signal feature extraction methods of radar anti-deception jamming [J]. Journal of University of Electronic Science and Technology, 2015, 44(1): 50-54.

[2] TAO B R. An ECCM model technical development trends to the demands of the future EW combat [J]. IEEE AES Systems Magazine, 1994, 9(6): 12-16.

[3] 王峰, 雷志勇, 黄桂根, 等. 雷达智能抗干扰体系研究 [J]. 现代雷达, 2014, 36(1): 80-82. WANG Feng, LEI Zhiyong, HUANG Guigen, et al. Intelligent anti-jamming technique in radar [J]. Modern Radar, 2014, 36(1): 80-82.

[4] SPARROW M J, CAKILO J. ECM techniques to counter pulse compression radar: 7081846 [P]. 2006-06-25.

[5] LI Y P, XIONG Y, TANG B. SMSP jamming identification based on matched signal transform [C]∥2011 International Conference on Computational Problem-Solving. Piscataway, NJ, USA: IEEE Computer Society, 2011: 182-185.

[6] ZHAO Y, DU D P, AHMED A A, et al. Detection of SMSP jamming in netted radar system based on fractional power spectrum [C]∥Proceedings of 17th IEEE International Conference on Computational Science and Engineering. Piscataway, NJ, USA: IEEE, 2014: 989-993.

[7] TAO A F, ZHENG J H, MEE M S, et al. Re-study on recurrence period of stokes wave train with high order spectral method [J]. China Ocean Engineering, 2011, 25(4): 679-686.

[8] CHEN C X, HE M H, XU J, et al. A new method for sorting unknown radar emitter signal [J]. Chinese Journal of Electronics, 2014, 23(3): 499-502.

[9] 郑红, 周雷, 杨浩. 基于谱峭度与双谱的轴承故障诊断方法 [J]. 北京航空航天大学学报, 2014, 40(9): 1176-1182. ZHENG Hong, ZHOU Lei, YANG Hao. Rolling element bearing fault diagnosis based on spectral kurtosis and bi-spectrum [J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(9): 1176-1182.

[10]王占领, 张登福, 王世强. 雷达辐射源信号双谱二次特征提取方法 [J]. 空军工程大学学报, 2014, 15(1): 48-52. WANG Zhanling, ZHANG Dengfu, WANG Shiqian. A method of feature extracting bispectrum cascade from radar emitter signal [J]. Journal of Air Force University, 2014, 15(1): 48-52.

[11]马兆宇, 韩福丽, 谢智东, 等. 卫星通信信号体系调制识别技术 [J]. 航空学报, 2014, 35(12): 3403-3414. MA Zhaoyu, HAN Ffuli, XIE Zhidong, et al. Modulation recognition technology of satellite communication signal system [J]. Acta Aeronautics et Astronautics Sinica, 2014, 35(12): 3403-3414.

[12]SHEN G J, STEPHEN M, XU Y C. Theoretical and experimental analysis of bispectrum of vibration signals for fault diagnosis of gears [J]. Mechanical Systems and Signal Processing, 2014, 43(1/2): 76-89.

[13]DU J X, ZHAI C M, WANG Q P. Recognition of plant leaf image based on fractal dimension features [J]. Neurocomputing, 2013, 116: 150-156.

[14]XU Y, QUAN Y H, ZHANG Z M, et al. Classifying dynamic textures via spatiotemporal fractal analysis [J]. Pattern Recognition, 2015, 48(10): 3239-3248.

[15]DU J X, ZHAI C M, WANG Q P. Recognition of plant leaf image based on fractal dimension features [J]. Neurocomputing, 2013, 116: 150-156.

[16]刘文涛, 陈红, 蔡晓霞, 等. 基于分形维数的数字调制信号识别 [J]. 火力与指挥控制, 2014, 39(10): 88-94. LIU Wentao, CHEN Hong, CAI Xiaoxia, et al. Digital modulation signal identification based on fractal dimension [J]. Fire Control & Command Control, 2014, 39(10): 88-94.

[17]何永亮, 陈西豪. 一种基于瞬时特征的电台个体识别方法 [J]. 计算机仿真, 2014, 31(9): 208-211. HE Yongliang, CHEN Xihao. Individual transmitter identification based on instantaneous feature [J]. Computer Simulation, 2014, 31(9): 208-211.

[18]李永平, 卢刚, 田晓, 等. 基于模糊函数的SMSP和C&I干扰识别算法 [J]. 航空兵器, 2011, 8(4): 51-54. LI Yongping, LU Gang, TIAN Xiao, et al. Jamming identification algorithms of SMSP and C&I based on ambiguity function [J]. Aero Weaponry, 2011, 8(4): 51-54.

(编辑 刘杨)

A Jamming Identification Method Against Radar Deception Based on Bispectrum Analysis and Fractal Dimension

YANG Shaoqi,TIAN Bo,ZHOU Ruizhao

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

A novel jammimg identification method based on bispectrum analysis and fractal dimension is proposed to solve the recognition problem of smeared spectrum (SMSP) and chopping and interleaving (C&I) interferences. Firstly, three-dimensional bispectrum information is obtained by performing bispectrum analysis on radar echoes. Then a two-dimensional feature curve is generated to reduce the calculation cost by using a dimension reducing method. Finally, characteristic parameters of the box dimension and the information dimension are extracted from the two-dimensional feature curve and used as the sorting characteristics. In addition, a support vector machine (SVM) method is used to test the interference recognition rate. Simulation results show that the proposed method is stable and its identification rate is over 88% when the signal-to-noise ratio is 0 dB, verifying the effectiveness of the proposed method.

radar; bispectrum analysis; fractal dimension; deception jamming; signal identification

2016-04-27。 作者简介:杨少奇(1992—),男,硕士生;田波(通信作者),男,副教授,硕士生导师。 基金项目:国家自然科学基金资助项目(61501500)。

时间:2016-10-10

10.7652/xjtuxb201612020

TN974

A

0253-987X(2016)12-0128-08

网络出版地址:http: ∥www.cnki.net/kcms/detail/61.1069.T.20161010.1751.004.html