利用参数结构的快速非酉联合对角化算法
2016-12-22刘文娟冯大政袁明冬
刘文娟,冯大政,袁明冬
(西安电子科技大学雷达信号处理国家重点实验室,710071,西安)
利用参数结构的快速非酉联合对角化算法
刘文娟,冯大政,袁明冬
(西安电子科技大学雷达信号处理国家重点实验室,710071,西安)
针对基于快速Frobenius范数对角化(FFDIAG)的盲信号分离算法不能直接处理复数数据从而导致分离性能差的问题,提出一种利用参数结构的快速非酉联合对角化(PSJD)算法。该算法首先将由观测信号的统计量得到的复目标矩阵转化为实对称矩阵;通过对代价函数的二阶近似,将解联合对角化问题转化为一系列的线性最小二乘问题,直接得到更新矩阵元素的估计。在每次迭代中,通过充分利用转化后的目标矩阵的结构信息,减少估计分离矩阵及更新目标矩阵的计算复杂度。同时,针对FFDIAG算法采用的固定步长难以兼顾收敛速度与更新矩阵严格对角占优性的问题,采用仅由当前更新矩阵的估计值决定的自适应学习率,提高算法的收敛性能。仿真实验表明,在一定的取值范围内,PSJD算法的收敛速度对步长参数的变化不敏感,在步长参数同为0.1的情况下,PSJD算法达到收敛所需的迭代次数比采用固定步长的算法减少了42%左右。
盲信号分离;联合对角化;目标矩阵;自适应学习率
盲信号分离(Blind Source Eeparation,BSS)由于其数学模型具有一般性,可适用于大多数观测数据,同时不需要训练序列或过多的先验信息,仅利用观测信号就可以有效恢复源信号,因此在电子侦察、无线通信、语音信号处理、图像处理及生物医学等领域具有广阔的应用前景[1]。基于联合对角化的BSS算法以其分离精度高、计算复杂度低而受到广泛关注。根据表征联合对角化近似程度的代价函数的不同,现有的联合对角化算法主要分为两大类:①利用目标矩阵非对角部分的Frobenius范数作为代价函数[2-5],最小化此代价函数直接得到分离矩阵的估计;②利用最小二乘代价函数[6-8]得到混迭矩阵的估计。这两类代价函数均为待估计的矩阵的四次函数,计算复杂度高。相对于基于Frobenius范数代价函数的算法,基于最小二乘代价函数的算法不仅需要估计混迭矩阵,还需要估计一组对角矩阵,而这些对角矩阵的取值通常是盲信号处理不关心的,从而导致待估计的未知参数数目增加;另一方面,当估计的混迭矩阵的条件数较大时,矩阵求逆运算将会放大其估计误差,从而影响算法性能。
在现有的基于Frobenius范数的非正交联合对角化算法中,Ziehe等提出的快速Frobenius对角化(Fast Frobenius DIA Gonalization,FFDIAG)算法[3]采用乘性迭代机制更新分离矩阵,在每次迭代中,利用更新矩阵及更新后的目标矩阵的非对角线元素很小的假设,对代价函数进行合理近似,将其转化为一个最小二乘问题,同时,利用矩阵的稀疏性直接计算更新矩阵的元素,避免矩阵求逆运算,该算法因其收敛性能好、计算复杂度低而受到广泛关注,但是其只能应用于实数域,无法直接推广至复数域。徐先锋等提出的复值快速Frobenius对角化(Complex-Valued Fast Frobenius DIA Gonalization,CVFFDIAG)算法[4]利用对未知参数的特殊表述,分开求解复未知参数的实部和虚部,将文献[3]算法推广至复数域,并利用Hessian矩阵的块对角结构,降低算法的计算复杂度。但是,该算法同FFDIAG一样,需要人为地选择一个步长因子θ(0<θ<1),使分离矩阵满足严格对角占优条件,保证分离矩阵可逆性。这一学习规则主要存在如下缺点:θ过小,算法收敛速度会降低;θ过大,则可能无法保证严格对角占优条件。
本文针对复数域联合对角化问题,提出一种利用参数结构的快速非酝酉联合对角化(PSJD)算法。通过将复矩阵转化为实对称矩阵,该算法将FFDIAG推广至复数领域,利用矩阵的特殊结构,提高算法性能、降低算法的计算复杂度,实现复目标矩阵组的联合对角化,同时该算法采用自适应学习率,避免固定的步长因子存在的问题。
1 矩阵结构信息
简要介绍复矩阵转化为实对称矩阵的方法[2],并详细分析转化后的矩阵的结构,为新算法的提出做准备。
1.1 复矩阵转化为实矩阵的方法
考虑K个维数为M×M的目标矩阵集合{R1,R2,…,RK},其中第k个目标矩阵Rk满足如下可联合对角化结构
(1)
式中:A为可逆的混迭矩阵;Dk为复对角矩阵。对于目标矩阵Rk,首先将其转化为2K个Hermitian矩阵[2]
(2)
式中:Re(·)和Im(·)分别表示取实部和虚部;i=(-1)1/2。其次,将这2K个维数为M×M的Hermitian矩阵转化为2M×2M的实矩阵[2]

(3)
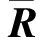
1.2 扩展的目标矩阵的结构
从式(2)和式(3)发现,扩展的目标矩阵具有如下结构信息。

(4)
(5)
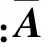
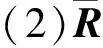
(6)
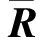
(7)
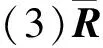
(8)
(9)
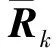
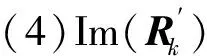
(10)
2 算法描述
2.1 PSJD算法
(11)
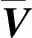
(12)
(13)
为推导简便,在不引起歧义的情况下,省略表示迭代次数的上标(t)和(t+1),代价函数可以表示为
(14)
式中:off(·)表示所有非对角线元素的平方和;wm,n和em,n,k分别表示W和Ek的第(m,n)个元素。定义子函数
J(wm,n,wn,m)=
(15)
可以看出,式(15)仅与元素wm,n和wn,m有关,所以,代价函数(14)可以分解为M(2M-1)个相互独立的子代价函数。由于扩展的目标矩阵组为2K个2M×2M维的矩阵,直接执行FFDIAG算法的运算量较大,下面将充分利用扩展的目标矩阵的结构信息,降低算法的计算复杂度。
由矩阵的结构信息可知,为使扩展的目标矩阵组在迭代过程中保持块一致结构,分离矩阵必须具有块一致结构,因此待估计的更新矩阵参数仅为2M(M-1)个。为充分利用上述结构,将更新矩阵分解为4个M×M维的子块独立地进行处理,具体步骤如下。
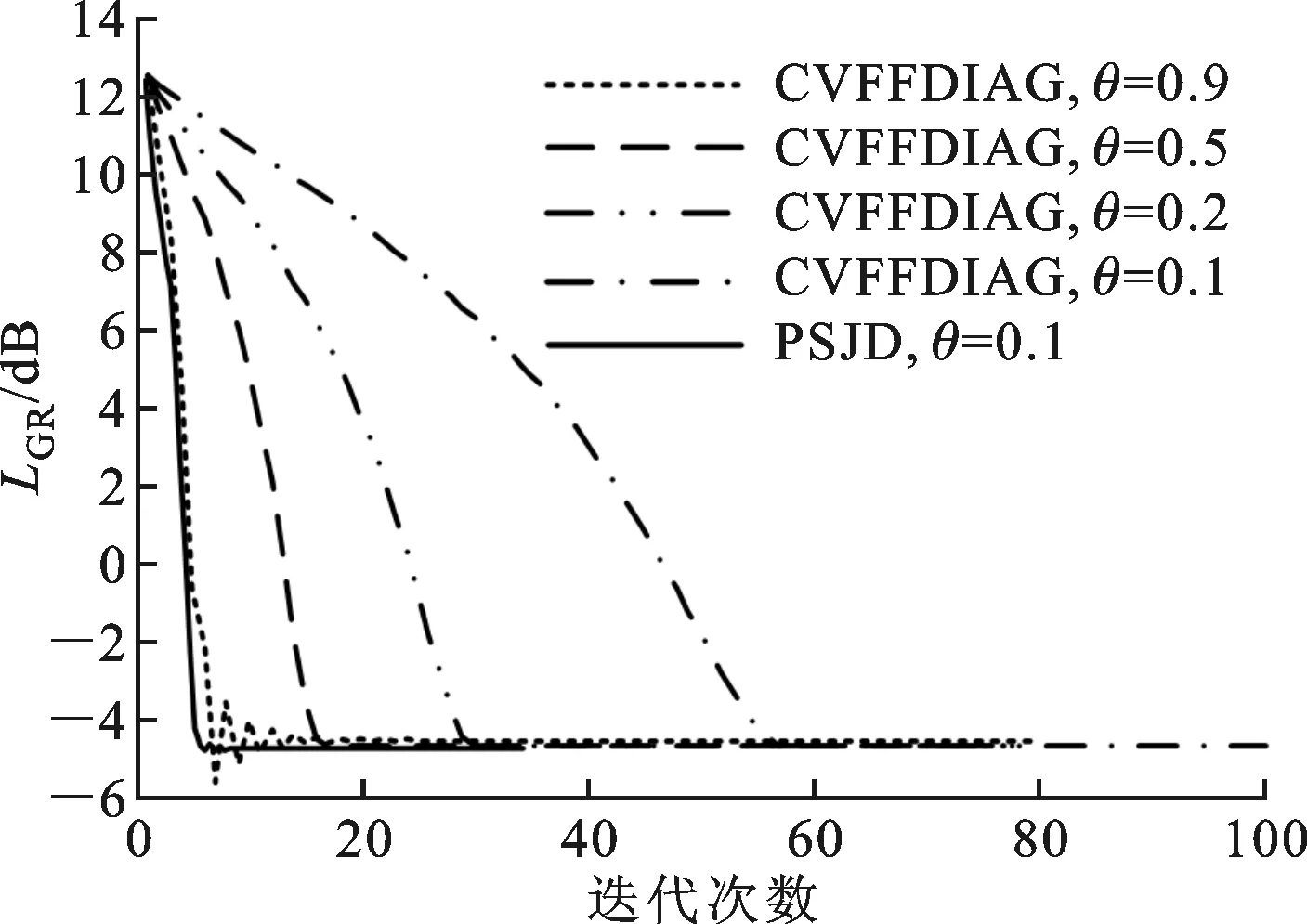
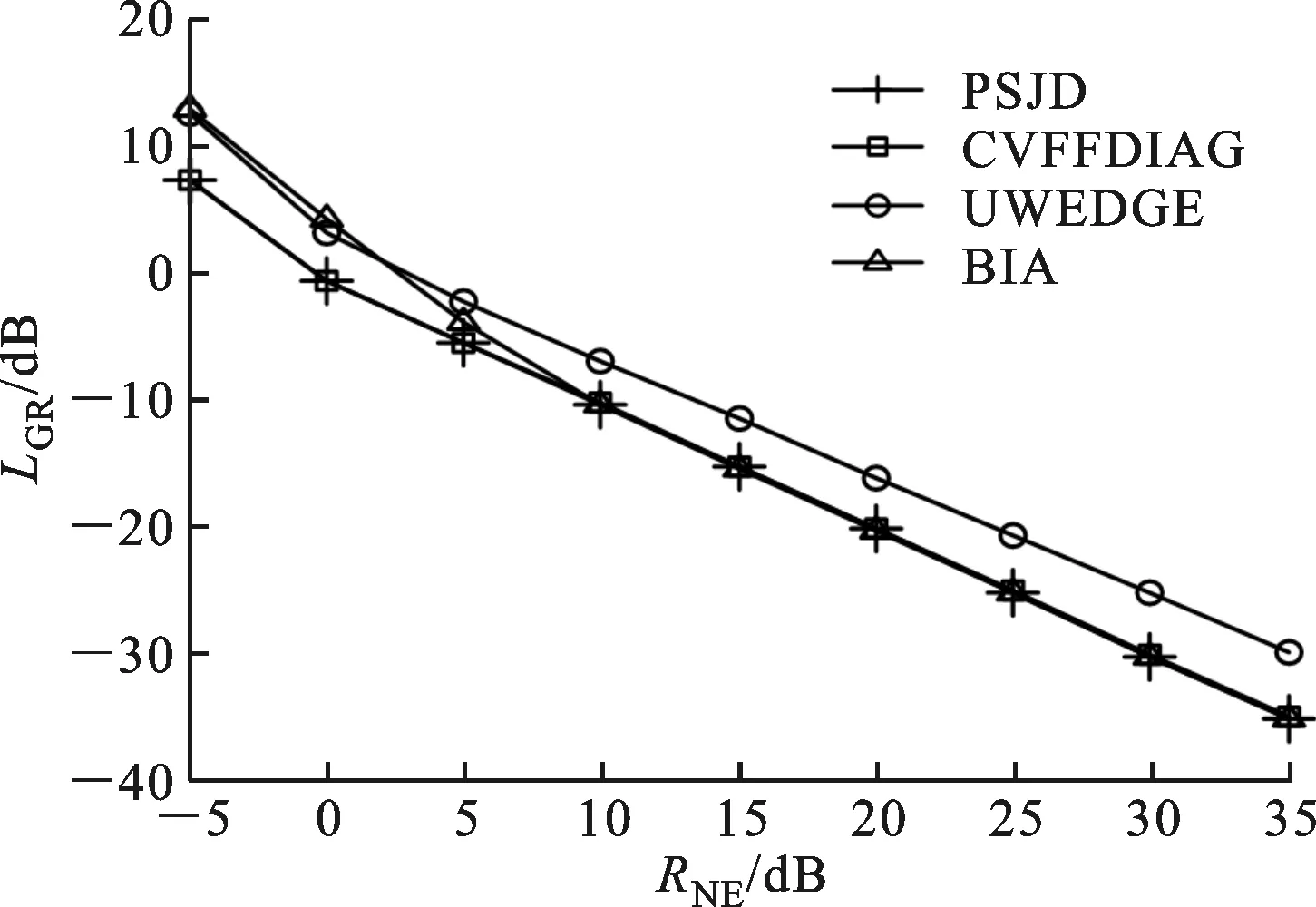
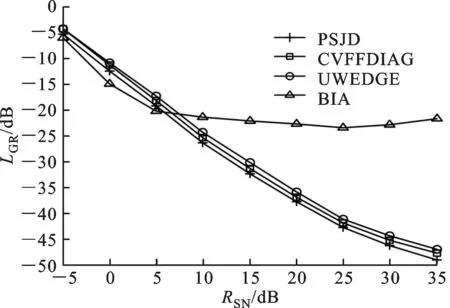
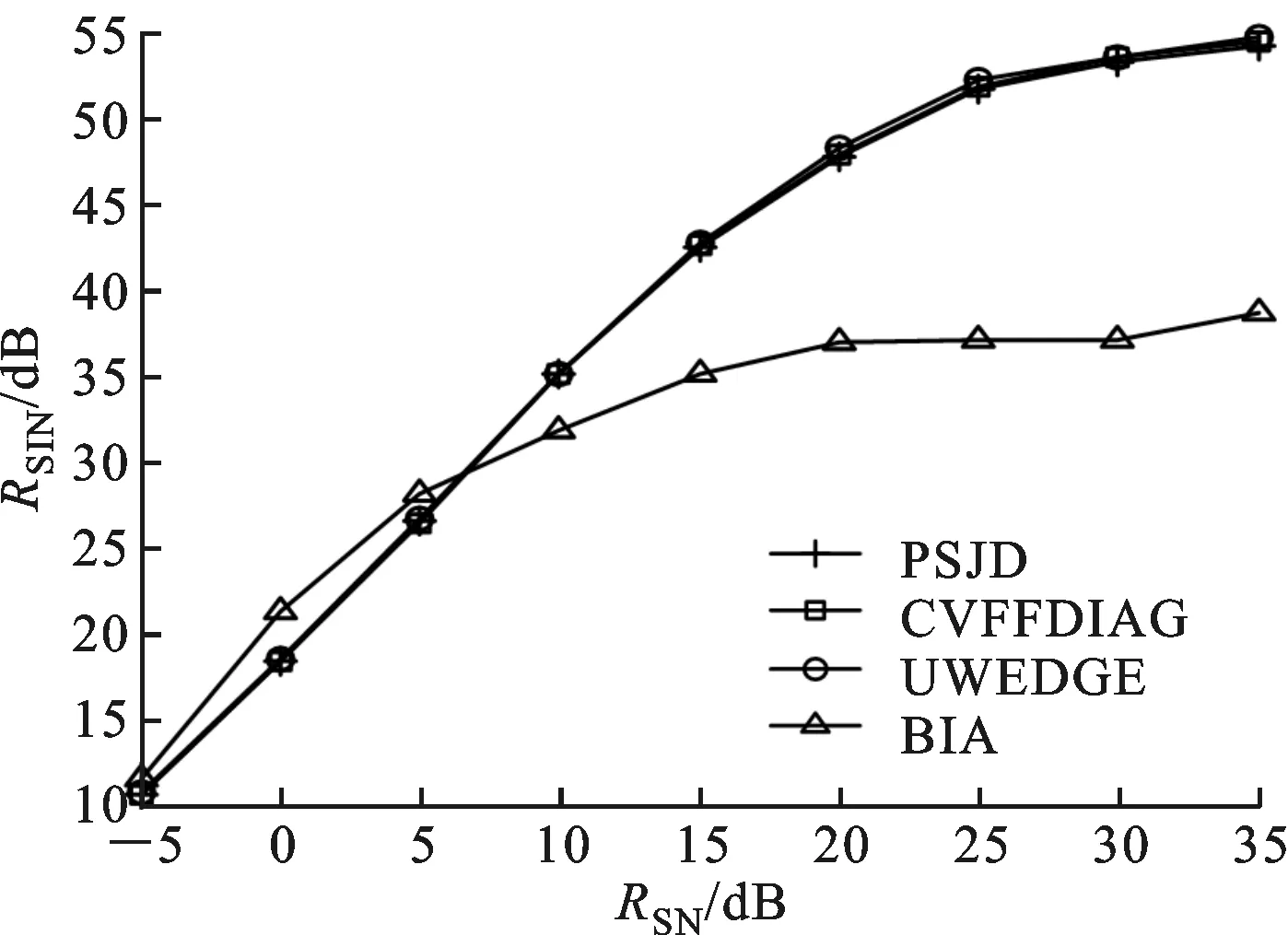
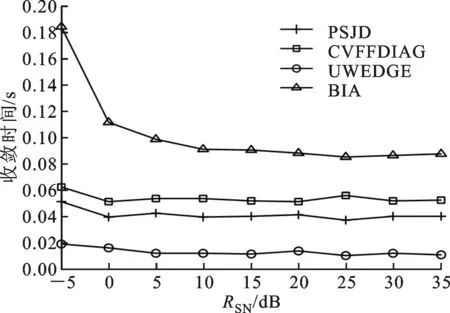
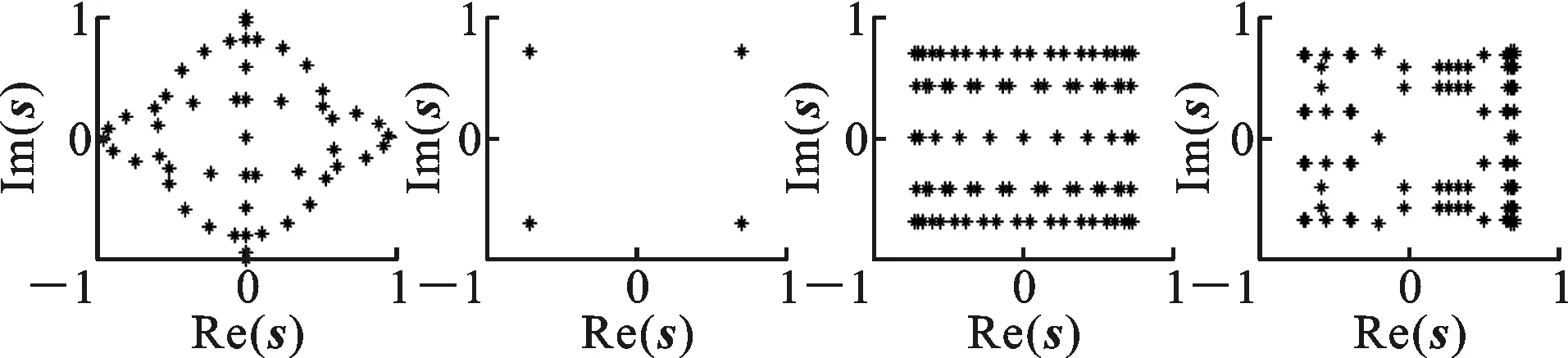
(1)假设1≤m (16) (17) (2)对于坐标为(m+M,n+M)的元素,利用块一致结构式(8)可将关于该子块内元素的代价函数表示为 (18) 该函数具有与式(16)相同的形式,该子块中元素的估计满足 (19) (3)对于坐标为(m,n+M)的元素,根据块一致结构式(8),关于该子块元素的优化问题式(15)可以写为 (20) 该子块中元素的最小二乘估计为 (21) (4)类似地,对于坐标为(m+M,n)的元素,由块一致结构式(8)和块内反对称结构式(7),该子块中元素的子代价函数为 (22) 对比式(20)和(22)可知 (23) (5)对于坐标为(m,m+M)的元素,由块一致结构式(8)和零对角结构式(10)可得 (24) 2.2 自适应学习率 2.3 算法步骤 利用PSJD算法实现复目标矩阵联合对角化的步骤总结如下。 输入 复目标矩阵组{R1,R2,…,RK}; 重复如下步骤,直至算法收敛: Fort=1,2,… 步骤1 根据如下子步骤估计更新矩阵W(t): Form=1,2,…,M-1;n=m+1,m+2,…,M (1)分别根据式(17)和(21)计算wm,n和wm,n+M; (2)分别根据式(19)和(23)计算wm+M,n+M和wn,m+M; (3)判断I+f-1(W(t))是否严格对角占优,如果不是,则W(t)⟸F(W(t))W(t); 步骤2 根据式(11)更新联合对角化矩阵,根据式(12)更新目标矩阵组; 考虑式(17)和(21)有相同的形式w=-B-1e,令B的第(i,j)个元素为Bi,j(i,j=1,2),利用 (25) 可以简化计算。 3.1 计算复杂度分析 由前文的分析可知,本文算法每次迭代(执行1次步骤1和2)需进行8M(M-1)K次实数乘除法运算(Number of Multiplications and Divisions,MDN),这里忽略了阶数低于O(M3K)和O(M4)的项。CVFFDIAG算法、基于高斯迭代的均匀加权完全对角化(Uniformly Weighted Exhaustive Diagonalization with Gauss Iterations,UWEDGE)算法[10]每次更新需进行8M3K次实数MDN,双迭代算法(bi-iterative algorithm,BIA)[7]每次迭代需进行12M3K次实数MDN。 3.2 收敛性分析 显然,代价函数C(V)的下界存在且大于等于零。这表明代价函数至少存在一个全局最小点。众所周知,非正交联合对角化为非线性优化问题,因此,严格的收敛性分析往往比较困难。通常借助于动力学理论中著名的Lyapunov函数和LaSalle’s不变定理[11-12]来分析算法的收敛性能。 (1)函数g(V(t))连续; (2)对于离散点t,有g(V(t))≤g(V(t-1)); 那么,g(V)称为Lyapunov函数。 (1)由于代价函数C(V)是可微分的,因此是连续的; 上述3点分析表明,代价函数是Lyapunov函数。根据定理1可知,离散序列V(t)收敛到C(V)的不变集UInvar。 综上分析,PSJD算法可渐进收敛到全局或至少是局部最小点。 通过与CVFFDIAG算法[4]、BIA算法[7]和UWEDGE算法[10]的比较,详细评估PSJD算法的性能。为了便于比较,采用盲信号分离算法中常用的性能参数——全局拒绝水平(Gglobal Rejection Level,GRL)[2-7,9,12]来衡量算法的有效性 (26) 式中:Gm,n为全局传输矩阵G=VA的第(m,n)个元素。全局拒绝水平LGR为一个非负的参数,描述了G与广义置换矩阵E=DP的接近程度,其中D为非奇异的对角阵(表示尺度不确定性),P为置换矩阵(表示排列不确定性)。LGR越小,表示G越接近于广义置换矩阵,分离性能越好。为了便于比较,在所有的实验中,若满足‖V(t)-V(t-1)‖F<ε则认为算法收敛,停止迭代,这里V(t)表示第t次迭代中分离矩阵的估计值。每个算法的最大迭代(扫描)次数设为500次,收敛门限ε=10-8。算法运行环境:MATLAB R2010a,Pentium(R) Dual-Core E5200 CPU @2.50 GHz,2 GB内存。 下面通过两组仿真实验比较各算法的性能。 图1 参数θ对收敛所需迭代次数的影响 图2 步长因子不同时2种算法的全局拒绝水平随迭代次数变化的曲线 为了评估参数选择对算法性能的影响,在RNE=0 dB的条件下进行了100次独立实验,得到PSJD算法和CVFFDIAG算法收敛所需的平均迭代次数随参数θ的变化曲线,如图1所示。可以看出,当θ为0.1、矩阵维数M分别为6、10、12、14时,PSJD算法所需迭代次数比CVFFDIAG算法分别减少约27%、42%、41%和39%,且参数θ越接近于1,算法的性能越稳健。图2表示在RNE=0 dB时PSJD算法(θ=0.1)以及CVFFDIAG算法取不同θ时的GRL随迭代次数变化的曲线。可以看出,θ的取值较大时,虽然收敛速度相对较快,但收敛状态不稳定,其原因主要是在迭代的初始阶段,更新矩阵及目标矩阵的非对角元素不满足范数很小的假设,较大的θ不能保证更新矩阵满足严格对角占优条件;而自适应学习规则分开考虑分离矩阵的每一行,仅对不满足条件的行赋予较小的步长,在确保更新矩阵满足严格对角占优条件的同时,保持较快的收敛速度,因而在收敛速度与收敛状态之间取得了一个很好的平衡。 (a)收敛LGR随RNE变化的曲线 (b)收敛所需时间随RNE变化的曲线图3 RNE对4种算法性能的影响 图3表示经过100次独立实验PSJD算法(θ=0.17)、CVFFDIAG算法(θ=0.9)、UWEDGE算法和BIA算法的收敛LGR和收敛时间随RNE变化的曲线。相应地,图4给出RNE=0 dB时,LGR随迭代次数变化的曲线。可以看出,PSJD算法具有与CVFFDIAG算法相似的收敛性能,且优于其他2个算法,PSJD算法的收敛所需的平均时间低于CVFFDIAG算法和BIA算法,高于UWEDGE算法,但平均LGR较UWEDGE算法降低了5 dB左右,与CVFFDIAG算法相比,得到相同的LGR所需时间更短。由4.1节可知,CVFFIDAG算法与PSJD算法每次迭代所需的MDN相同,图3b可间接说明PSJD算法比CVFFDIAG算法的平均收敛速度更快。UWEDGE算法的参数更新是以向量或矩阵的形式进行的,避免了大量的循环迭代,因此在MATLAB环境下效率更高,而BIA算法在两组参数间交替迭代,计算复杂度最高,收敛速度最慢。 图4 4种算法的全局拒绝水平随迭代次数变化的曲线 实验2 采用一组复信号测试所提算法应用于盲信号分离的性能。源信号为4个0均值的相互独立的复信号 (27) 采样点数为1 000,接收阵列为7个阵元构成的均匀线阵,阵元间距半波长,即混迭矩阵A=[a(φ1),a(φ2),…,a(φ4)],a(φ)=[1,e-iπcosφ,…,e-i6πcosφ]T,各信号的入射角度分别为φ1=20+10γ,φ2=50+15γ,φ3=75+10γ,φ4=115+15γ,其中,γ∈[0,1]随机产生。取时延为3k(k=1,2,…,15)构造目标矩阵组,由于混迭矩阵为高矩阵,因此需要一个白化降维预操作。为衡量算法的分离性能,采用估计信号的信干噪比来表征分离信号的独立性,信干噪比为 (28) (a)收敛LGR随RSN变化的曲线 (b)收敛信干噪比随RSN变化的曲线 (c)收敛时间随RSN变化的曲线 (d)迭代次数随RSN变化的曲线图5 信噪比对4种算法性能参数的影响 图5为经过100次独立实验,4种算法的平均性能参数随信噪比RSN变化的曲线。可以看出,由于预白化的影响,4种算法的分离性能相近,但PSJD算法(θ=0.1)与CVFFDIAG算法(θ=0.9)、BIA算法相比,得到相近的LGR所需的迭代次数和时间较少。这是因为即使W(t)的某些行不满足严格对角占优条件,CVFFDIAG算法所用的固定步长都对W(t)所有行进行调节,这将使W(t)相对于其最优值产生较大的偏离,从而影响收敛速度;而PSJD算法采用的自适应学习率对W(t)的每行分开考虑,某行的1-范数越小则说明经过t-1次迭代,该行对应的分离信号与源信号越接近,因此无需对该行进行处理,从而提高了算法的收敛速度。同时,这也是‖W(t)‖F<ε可以作为此算法收敛条件的原因。图6表示RSN=25 dB时,源信号和对应的分离信号的星座图,可见所提算法能够有效地恢复源信号。 (a)s1(t)(b)s2(t)(c)s3(t) (d)s4(t) 图6 源信号、分离信号的星座图 本文通过将复矩阵转化为实对称矩阵,将FFDIAG算法推广至复数域,利用转化后的目标矩阵的结构信息,降低算法的计算复杂度。同时,采用自适应学习规则,改善了在初始迭代状态中,更新矩阵和目标矩阵的非对角部分不满足假设条件时,采用固定步长因子无法确保严格对角占优性而导致收敛状态不稳定的情况,确保了分离矩阵的可逆性,且避免了收敛速度对参数选择的依赖,提高了算法的收敛性能。仿真实验表明,同CVFFDIAG算法相比,本文所提PSJD算法达到相同的全局拒绝水平所需的运算时间更短。 [1] CHABRIEL G, KLEINSTEUBER M, MOREAU E, et al. Joint matrices decompositions and blind source separation: a survey of methods, identification, and applications [J]. IEEE Signal Processing Magazine, 2014, 3(31): 34-43. [2] MESLOUB A, ABED-MERAIM K, BELOUCHRANI A. A new algorithm for complex non orthogonal joint diagonalization based on Shear and Givens rotations [J]. IEEE Transactions on Signal Processing, 2014, 62(8): 1913-1925. [3] ZIEHE A, LASKOV P, NOLTE G, et al. A fast algorithm for joint diagonalization with non-orthogonal transformations and its application to blind source separation [J]. Journal of Machine Learning Research, 2004, 5(3): 777-800. [4] XU Xianfeng, FENG Dazheng, ZHENG Weixing. A fast algorithm for nonunitary joint diagonalization and its application to blind source separation [J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3457-3463. [5] 丛丰裕, 雷菊阳, 许海翔, 等. 在线增强型复值混合信号盲分离算法研究 [J]. 西安交通大学学报, 2006, 40(9): 1070-1073. CONG Fengyu, LEI Juyang, XU Haixiang, et al. Online blind separation of enforced mixed complex-value signal sources [J]. Journal of Xi’an Jiaotong University, 2006, 40(9): 1070-1073. [6] 聂卫科, 冯大政, 刘建强. 二维波达方向估计的非酉联合对角化方法 [J]. 西安交通大学学报, 2008, 42(6): 747-750. NIE Weike, FENG Dazheng, LIU Jiangiang. Non-unitary joint diagonalization method for estimating two-dimension direction of arrival [J]. Journal of Xi’an Jiaotong University, 2008, 42(6): 747-750. [7] FENG Dazheng, ZHANG Hua, ZHENG Weixing. Bi-iterative algorithm for extracting independent components from array signals [J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3636-3646. [8] ZENG Tiaojun, FENG Quanyuan. Non-orthogonal joint diagonalization algorithm based on hybrid trust region method and its application to blind source separation [J]. Neurocomputing, 2014, 133(8): 280-294. [9] 陆建涛, 成玮, 訾艳阳, 等. 变步长等变自适应盲源分离算法 [J]. 西安交通大学学报, 2015, 49(12): 83-89. LU Jiantao, CHENG Wei, ZI Yanyang, et al. Variable step-size algorithm for equivariant adaptive separation via independent [J]. Journal of Xi’an Jiaotong University, 2015, 49(12): 83-89. [10]TICHAVSKY P, YEREDOR A. Fast approximate joint diagonalization incorporating weight matrices [J]. IEEE Transactions on Signal Processing, 2009, 57(3): 878-891. [11]LASALLE J P. The stability of dynamical system [M]. Philadelphia, PA, USA: SIAM Press, 1976: 49-50. [12]张伟涛, 楼顺天, 张延良. 非对称非正交快速联合对角化算法 [J]. 自动化学报, 2010, 36(6): 829-836. ZHANG Weitao, LOU Shuntian, ZHANG Yanliang. Non-symmetrical non-orthogonal fast joint diagonalization algorithm [J]. Acta Automatica Sinica, 2010, 36(6): 829-836. [本刊相关文献链接] 王玉玺,黄国策,李伟,等.非均匀广义对角加载稳健波束形成算法.2016,50(8):64-69.[doi:10.7652/xjtuxb201608011] 刘健伶,陈志刚,王磊.一种自适应广义空间调制及其低复杂度算法.2016,50(4):48-53.[doi:10.7652/xjtuxb201604008] 王富平,水鹏朗.采用多尺度方向微分比率的角点检测算法.2016,50(4):68-75.[doi:10.7652/xjtuxb201604011] 赵凯,王闯,李尊朝,等.结合平衡和滤波技术抑制GaN电源转换器的电磁干扰.2016,50(02):38-42.[doi:10.7652/xjtuxb201602007] 孙黎,徐洪斌.协作式终端直通系统中星座旋转辅助的干扰避免策略.2015,49(12):6-11.[doi:10.7652/xjtuxb201512 002] 张东伟,郭英,齐子森,等.采用空间极化时频分布的跳频信号多参数联合估计算法.2015,49(8):17-23.[doi:10.7652/xjtuxb201508004] 巴斌,郑娜娥,朱世磊,等.利用蒙特卡罗的最大似然时延估计算法.2015,49(8):24-30.[doi:10.7652/xjtuxb201508005] 吴一全,孟天亮,吴诗婳.人工蜂群优化的非下采样Shearlet域引导滤波图像增强.2015,49(6):39-45.[doi:10.7652/xjtuxb201506007] 熊涛,江桦,崔鹏辉,等.应用基扩展模型的混合信号单通道盲分离算法.2015,49(6):60-66.[doi:10.7652/xjtuxb201506 010] 郝雯洁,齐春.一种鲁棒的稀疏信号重构算法.2015,49(4):98-103.[doi:10.7652/xjtuxb201504016] 王云龙,吴瑛.联合时延与多普勒频率的直接定位改进算法.2015,49(4):123-129.[doi:10.7652/xjtuxb201504020] 尚佳栋,王祖林,周丽娜,等.采用随机共振增强的混合扩频信号跳频参数估计.2014,48(10):42-48.[doi:10.7652/xjtuxb201410007] 储颖,牟轩沁,洪伟.采用形状一致性特征的盲图像质量评价方法.2014,48(8):12-17.[doi:10.7652/xjtuxb201408003] 吴仁斌,姚敏立,贾维敏,等.采用幅度响应约束的鲁棒自适应波束形成算法.2014,48(4):109-114.[doi:10.7652/xjtuxb201404019] 郝红侠,刘芳,焦李成,等.采用结构自适应窗的非局部均值图像去噪算法.2013,47(12):71-76.[doi:10.7652/xjtuxb 201312013] 穆为磊,高建民,王昭,等.考虑人眼视觉特性的射线检测数字图像质量评价方法.2013,47(7):91-95.[doi:10.7652/xjtuxb201307017] (编辑 刘杨) A Fast Non-Unitary Joint Diagonalization Algorithm Based on Utilizations of Parametric Structures LIU Wenjuan,FENG Dazheng,YUAN Mingdong (National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China) A parametric structures based fast joint diagonalization (PSJD) algorithm for non-unitary diagonalization of a set of complex target matrices is presented to cope with the problem that the blind source separation by fast Frobenius diagonalization (FFDIAG) algorithm is not applicable in the complex-valued space and its separation performance is lower. The algorithm firstly transforms the complex target matrices into real-symmetric ones. Secondly, the problem of simultaneous diagonalization of matrices is transformed into a series of linear least-squares problems through second-order approximation to contract functions, and the elements of the updating matrix are directly estimated. The computational complexity for estimating the diagonalizer and for updating the target matrices is significantly reduced by making full use of the structure information of the transformed target matrices. In order to overcome the drawback of fixed step size adopted in the FFDIAG that may not strike a balance between the convergence rate and strictly diagonally dominant property of the update matrix, the proposed algorithm uses the adaptive learning rate determined from the estimation of the update matrix in each iteration to improve the convergence property. Results of numerical simulations show that the convergence rate of PSJD algorithm is not very sensitive in a wide range of step-size values. When the step size is 0.1, the number of iterations required to reach convergence is 42% less than that of the fixed step-size method. blind source separation; joint diagonalization; target matrix; adaptive learning rate 2016-03-08。 作者简介:刘文娟(1986—),女,博士生;冯大政(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61271293,61373177)。 时间:2016-10-10 10.7652/xjtuxb201612017 TN911.7 A 0253-987X(2016)12-0106-08 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20161010.1743.002.html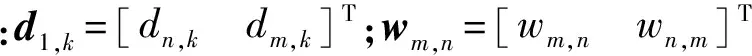

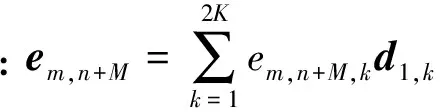
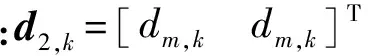
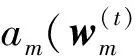

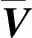
3 性能分析
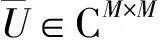



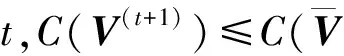
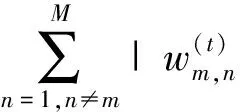
4 仿真实验
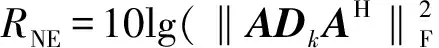






5 结 论
