一种分析微带线随机参数敏感性的多项式混沌展开方法

程市,黄斌科,师振盛

(西安交通大学电子与信息工程学院,710049,西安)



一种分析微带线随机参数敏感性的多项式混沌展开方法

程市,黄斌科,师振盛

(西安交通大学电子与信息工程学院,710049,西安)

针对传输线加工中材料及结构参数随机不确定性对传输性能影响的问题,提出了一种计算随机系数传输线电报方程的多项式混沌(PC)展开方法。利用正交多项式混沌基函数,该方法首先将传输线电报方程中的随机等效集总参数、传输线电压及电流响应进行展开;其次利用Galerkin法,将随机系数的电报方程问题转化为关于电压、电流正交多项式展开系数的确定性扩阶方程组问题,并结合传输线边界条件可计算电压、电流的展开系数,进而获得电压、电流及传递函数的均值、方差和概率密度分布。随机参数微带传输线的仿真结果表明:低频时导带宽度对微带线的传输性能影响较大,高频时介电常数对其传输性能影响较大;在满足计算精度要求的同时,PC展开方法具有比传统蒙特卡罗(MC)方法更高的计算效率,计算耗时仅约为MC方法的1/500。

微带线;电报方程;敏感性;多项式混沌展开;蒙特卡罗方法

微带线在集成电路互连和平面微波电路设计中有着广泛的应用。随着电路器件的小型化和集成度的提高,微带线加工中的材料和几何结构参数的随机不确定性对微带电路的影响越来越严重,因此研究加工参数随机不确定性对微带电路性能的影响,并分析电路响应对加工随机参数的敏感性,对于平面微波电路设计具有重要的应用价值,且可以兼顾性能余量和加工成本问题。

目前在电磁及微波领域研究随机问题的典型方法为蒙特卡罗(MC)方法和多项式混沌(PC)方法等。MC方法对随机模型参数进行大量采样并进行多次统计实验,得到随机响应的统计特性。文献[1]和文献[2]结合精细积分算法和MC方法对工艺参数随机扰动下的传输线进行了建模和分析,给出了传输线随机模型的瞬态响应。该方法具有易于实现的优点,但其统计结果要达到收敛需要大量的采样样本,耗费时间长,计算效率低。文献[3]提出了一种将拉丁超立方采样与MC方法相结合的方法,该方法在一定程度上可减小MC方法的采样数量,提高了采样效率。目前工程应用中一般将MC方法作为对其他随机问题计算算法效率的评价标准。PC方法基于随机变量的概率分布,利用正交多项式混沌对随机过程进行展开,并结合响应随机变量的控制方程及Galerkin方法可将随机模型转化为扩阶的确定性问题进行求解,进而得到响应的统计特性[4]。文献[5]在研究带通滤波器电路中温度随机变化对电路响应的影响时,采用PC方法对节点方程组中的随机变量进行展开,较MC方法具有精确快速的优点。文献[6]和文献[7]研究传输线互连问题时,将PC方法引入到传输线方程,计算了材料和结构参数随机不确定时的传输响应,验证了PC方法的正确性及高效性,但没有分析加工参数随机性对传输性能影响的敏感性。文献[8]提出了一种基于PC方法和进化算法相结合的电磁场逆问题鲁棒优化设计方法,引入PC方法后有效降低了计算资源。然而,上述文献没有分析加工参数随机性对传输线尤其是微带线性能影响的敏感性。

本文将PC方法引入随机参数的传输线方程,分析微带线传输响应受基板材料及导带几何尺寸随机影响的敏感性。首先介绍了PC展开理论,并针对随机参数的传输线方程将PC展开与Galerkin方法结合,将随机问题的求解转化为扩阶的确定性方程组的求解;其次,以微带线为例,研究微带线参数随机变化时传输响应的统计特性;最后分析微带线传输的影响应受随机参数影响的敏感性。本文方法与传统MC方法相比在计算效率上有显著优势。

1 多项式混沌展开理论

若Z为一维随机变量,则关于随机变量Z的函数f(Z)的多项式混沌逼近为

(1)

正交多项式基函数的选取与随机变量Z的概率密度分布函数ρ(Z)有关,不同概率分布的随机变量可选择不同的Askey正交多项式作为最优逼近的基函数[9]。Xiu等人从Askey多项式族出发,将基于高斯随机变量的Hermite多项式混沌展开拓展到其他不同概率密度分布的随机变量的Askey PC族[4],如Gamma分布对应Laguerre多项式基展开、Beta分布对应Jacobi多项式基展开和均匀分布对应Legendre多项式基展开等。将一维随机变量拓展到多维独立随机变量的正交多项式展开时,对n维相互独立的随机变量采用m阶PC展开逼近,PC展开项数P+1=(n+m)!/(n!m!)[4,9]。如对2维独立随机变量采用3阶、5阶、7阶展开时,对应的展开项分别为10项、21项、36项。

PC展开理论中,利用有限项正交多项式混沌之和的形式表示随机参数,并代入到随机偏微分方程中实现系统响应求解,系统响应的随机统计特性如均值、方差、概率密度等可解析表示。PC展开方法只需一次仿真,这是PC展开方法相较于传统MC方法的优势所在。

2 微带线随机参数传输线方程计算

以微带线模型为例,图1所示的为含源和负载的传输线电路。传输线理论中,将传输线分布参数效应用其单位长度等效集总参数电路进行分析[10]。采用基尔霍夫电压和电流定律得到关于传输线上电压、电流满足的电报方程

(2)

式中:R、L分别为单位长度传输线串联电阻和电感;G、C分别为并联电导和电容;s=jω为拉普拉斯变换域复变量。为书写方便,令串联复数阻抗Z=R+sL,复数导纳Y=G+sC。

E(s)为电压源;ZS和ZL分别为电压源内阻和负载;V1(s)和V2(s)分别为近端电压和远端电压;I1(s)和I2(s)分别为近端电流和远端电流;l为传输线长度图1 含源和负载的传输线电路

在加工中,实际微带线结构模型的基板材料参数εr、基板高度h和导带宽度w等受加工工艺的影响会存在随机不确定性,进而对微带线作为传输互连结构时的性能产生影响。本文考虑基板材料相对介电常数εr和导带宽度w近似服从高斯分布

(3)

(4)

利用PC理论,传输线方程中的随机变量系数阻抗、导纳可用正交多项式基函数展开,这些正交多项式基函数与傅里叶级数中的正余弦函数类似。对于阻抗、导纳变量服从高斯随机分布,其对应的正交基函数为Hermite多项式。将微带线电报方程阻抗、导纳随机变量用Hermite正交多项式展开如下

(5)

(6)

式中:ξ为随机矢量,ξ=[ξ1,ξ2]T;Zk、Yk为展开系数,其计算公式如下

(7)

(8)

对于展开系数Zk和Yk的计算,阻抗、导纳对于结构较复杂的传输线无解析表达式,通常采用高斯数值求积方法得到。电压、电流响应随机变量用Hermite正交多项式展开如下

(9)

(10)

式中:Vj和Ij为待求的展开系数,将式(5)、(6)、(9)、(10)代入电报方程(2),可得

(11)

(12)

对式(11)、(12)应用随机Galerkin方法展开,得到

(13)

(14)

令

(15)

(16)

式中:P为展开项数。

将式(15)、(16)代入到式(13)、(14)中,将得到关于电压、电流展开系数的方程组

(17)

利用式(17),微带线终端电压V2、电流I2与始端电压V1、电流I1的关系为

(18)

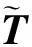
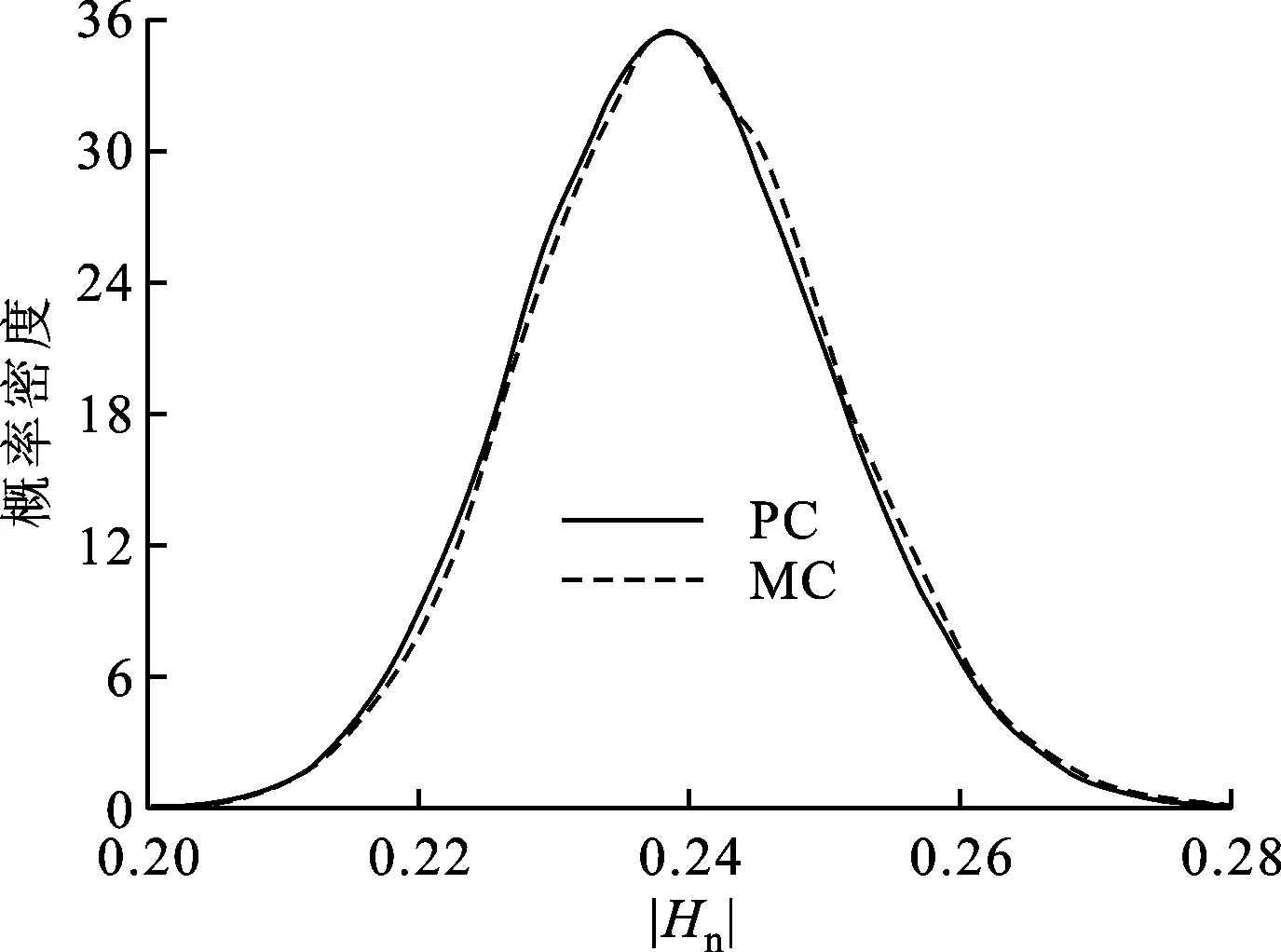
(19)

考虑图1中源和负载的边界条件

(20)

(21)

式中:V1和V2分别为始端和终端电压;I1和I2分别为始端和终端电流;ZS和ZL分别为始端和终端阻抗;E(s)为激励电压源。将式(20)、(21)用PC方法展开并结合式(18),得到关于电压、电流展开系数的矩阵方程

(22)

式(19)中的各项都是用PC方法展开后得到的系数矩阵,求解式(19)得到电压、电流展开系数后,结合Hermite正交多项式基函数可得到关于电压、电流及传递函数的统计特性如均值、方差和概率密度函数等,由计算得到的统计结果可用于分析微带传输线传输性能受其材料及结构参数随机性的敏感性。

上述理论是在考虑传输线等效集总RLGC参数影响条件下给出的,对一般结构较复杂的传输线,其频散RLGC参数并没有明确的解析表达式。对PC展开中需要的受频率和传输线结构及材料参数影响的RLGC计算,通常引入宏模型来表征以提高计算精度和效率[12]。对于工作频率较低或结构尺寸较大的传输线模型可忽略传输损耗的影响,只需分析加工随机参数对传输相移的敏感性,可有效降低本文算法的计算复杂度。

3 微带线模型仿真与分析

为简洁起见,本文算例考虑无耗传输线工作状态。以微带线模型为例,导带厚度t=35 μm,基板介质高度h=60 μm,微带线长度l=5 cm。图1所示传输线电路中激励电压源为正弦信号,源阻抗ZS=50 Ω,负载阻抗ZL=1/(sCL+GL),其中CL=10 pF,GL=1/(10 kΩ)。微带线基板介质相对介电常数εr和微带线导带宽度w均服从高斯分布,εr均值取3.7,w均值为100 μm,两个随机变量的相对标准偏差均取0.1。

本文方法在实现中,考虑导带厚度、电容、电感作为微带线基板材料介质参数、基板介质高度、微带线导带宽度等的函数可利用解析公式进行求解[13]。求解式(6)、(7)对应的电容、电感展开系数时,采用数值求积方法结果精度高且易于实现。这里分别计算了微带线的近端传递函数Hn=V1(s)/E(s)和远端传输函数Hf=V2(s)/E(s)。本文同时也给出了MC方法的计算结果,以验证本文PC方法计算结果的正确性,在MC方法中采样次数取40 000,满足统计结果的收敛性。

3.1 微带线基板介质相对介电常数随机变化

只考虑微带线基板介质相对介电常数εr随机变化,微带线其他参数都是确定性的。采用一维3阶正交Hermite多项式基函数,展开项数P=4。图2a和2b分别为微带线近端和远端传输传递函数在0.3 GHz时的概率密度分布,本文PC方法结果和MC方法结果取得了较好的一致性。从图2a中可见近端传递函数取值大致在0.2～0.28区间,图2b所示远端传递函数取值大致在0.73～0.83区间。

(a)近端

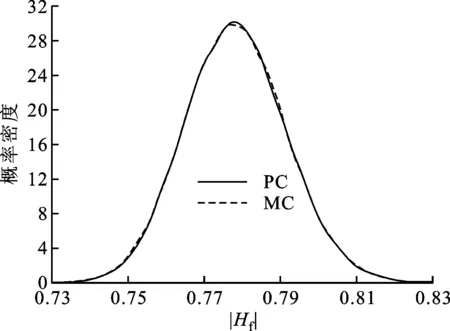
(b)远端图2 εr随机变化时传递函数的概率密度分布

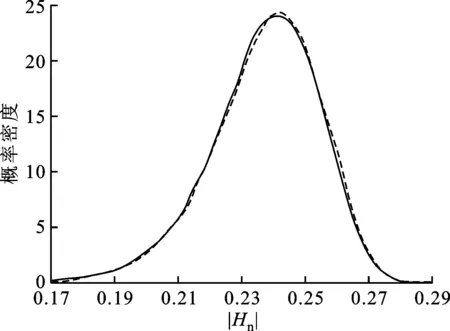
(a)近端

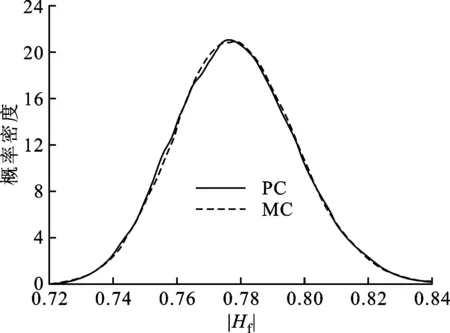
(b)远端图3 w随机变化时传递函数的概率密度分布

3.2 微带线导带宽度随机变化

只考虑导带宽度w随机变化,微带线其他参数都是确定性的。同样采用一维3阶正交Hermite多项式基函数,展开项数P=4。图3a和3b分别为微带线近端和远端传递函数在0.3 GHz时的概率密度分布,本文PC方法结果和MC方法结果同样取得了较好的一致性。由图3a可见近端传递函数取值大致在0.17～0.29区间,图3b所示远端传递函数取值大致在0.72～0.84区间。

3.3 微带线基板介质相对介电常数和导带宽度均随机变化

考虑微带线基板介质相对介电常数εr和导带宽度w均随机变化,微带线其他参数确定。采用二维3阶正交Hermite多项式基函数,展开项数P=10。图4a和4b分别为微带线近端和远端传递函数在0.3 GHz时的概率密度分布,本文PC方法结果和MC方法结果同样取得了较好的一致性,说明3阶PC方法有较高的精度。对于二维随机变量的响应,其概率也近似服从高斯分布。由图4a可见近端传递函数取值大致在0.16～0.31区间,图4b所示远端传递函数取值大致在0.70～0.86区间。

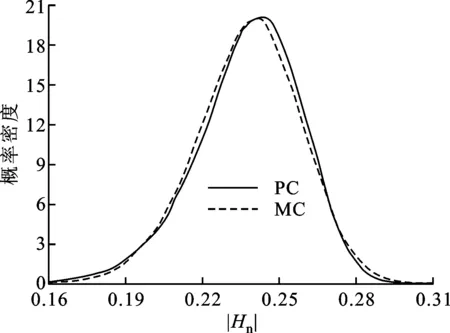
(a)近端

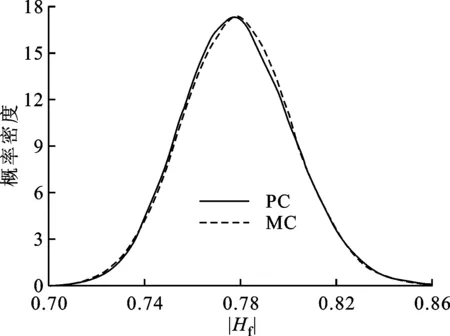
(b)远端图4 εr和w随机变化时传递函数的概率密度分布

利用仿真得到的微带线传输函数概率密度分布,可计算其均值和标准偏差,并利用3σ准则可对传递函数受微带线随机材料和结构尺寸参数变化的上、下界给出估计。表1～表3分别给出了0.3、1.3和2.3 GHz时近端、远端传递函数随微带线基板介质相对介电常数εr和导带宽度w随机变化时的均值和偏离均值的上、下界估计值。

从表1～表3对比发现:①在相同的标准偏差下,1.3 GHz和2.3 GHz时相对介电常数εr随机变化对近端传递函数的影响较大,而在0.3 GHz时导带宽度w随机变化对近端传递函数的影响较大,因此在低频时近端响应受导带宽度不确定性的敏感性大,而高频时近端响应受基板介质参数不确定性的敏感性大;②在相同的标准偏差下,远端传递函数受导带宽度w随机不确定性的影响稍大于相对介电常数εr的不确定性影响,但差别不大;③近端传递函数随着频率增加而增大,而远端传递函数随着频率增加而减小;④对于两个随机变量均考虑时的传递函数,其3σ上下界范围均比单个随机变量时的上下界范围要宽,即两个随机变量时的传递函数的标准偏差比单个随机变量要大,说明微带线加工中多个参数随机变化时对传输性能的影响更大。另外从表1～表3中3种不同随机参数情况的比较可见,微带线传递函数响应主要受制于对其敏感性影响更大的加工参数,因此在微带线加工中对不同材料及结构参数可分类采用不同的加工精度,以兼顾加工质量和成本。

表1 0.3 GHz时近端和远端传递函数3σ上下界估计及均值

表2 1.3 GHz时近端和远端传递函数3σ上下界估计及均值

表3 2.3 GHz时近端和远端传递函数3σ上下界估计及均值

为了说明PC展开方法处理随机参数传输线互连问题的高效性,表4给出了PC方法和MC方法在微带线输入随机参数在3种情况下的计算耗时比较,从计算耗时上看,对一维和二维随机变量问题的求解,PC方法的计算时间仅约为MC方法的1/500,因此本文PC方法与传统MC方法相比大大节约了计算时间。

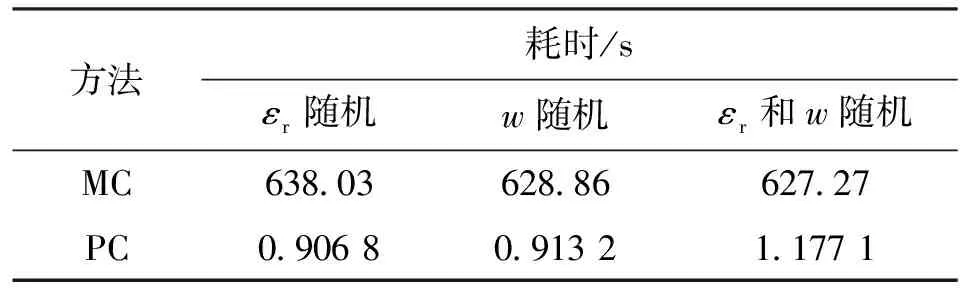
表4 本文PC方法和MC方法计算耗时比较

4 结 论

本文将PC展开理论引入到随机参数的传输线方程计算中,通过计算微带线基板介质介电常数及微带线导带宽度随机变化时传输响应的统计特性,可有效分析微带线加工参数不确定性对其传输性能的影响,可为微带线传输互连结构及平面微波电路设计中的加工容差给出指导。通过对微带线随机传输响应的均值及仿真计算,结果表明低频时导带宽度对微带线传输性能影响较大,高频时介电常数对传输性能影响较大。本文方法在保证计算精度的同时在计算耗时上仅约为传统MC方法的1/500。本文后续工作中将对导带横截面更小的微带线模型,考虑其导体损耗,分析受加工参数不确定性对高频段微波传输互连性能影响的敏感性问题。

[1] 张瑛, WANG J M, 肖亮, 等. 工艺参数随机扰动下的传输线建模与分析新方法 [J]. 电子学报, 2005, 33(11): 1959-1964. ZHANG Ying, WANG J M, XIAO Liang, et al. A new stochastic modeling and analysis method for transmission lines in the presence of random process variations [J]. Acta Electronica Sinica, 2005, 33(11): 1959-1964.

[2] 张瑛, WANG J M, 肖亮, 等. 传输线的随机建模及瞬态响应数值实验分析 [J]. 电子与信息学报, 2006, 28(8): 1516-1520. ZHANG Ying, WANG J M, XIAO Liang, et al. Stochastic modeling for transmission lines and numerical experimental analysis for transient simulation [J]. Journal of Electronics & Information Technology, 2006, 28(8): 1516-1520.

[3] 徐小宇. 大规模集成电路中工艺参数影响的随机有限元法分析 [D]. 北京: 中国科学院电工研究所, 2009: 59-68.

[4] XIU D, KARNIADAKIS G E. The Wiener-Askey polynomial chaos for stochastic differential equations [J]. SIAM Journal on Scientific Computing, 2003, 24(2): 619-644.

[5] SU Q, STRUNZ K. Stochastic circuit modelling with Hermite polynomial chaos [J]. Electronics Letters, 2005, 41(21): 1163-1165.

[6] STIEVANO I S, MANFREDI P, CANAVERO F G. Parameters variability effects on multiconductor interconnects via Hermite polynomial chaos [J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2011, 1(8): 1234-1239.

[7] MANFREDI P, STIEVANO I S, CANAVERO F G. Parameters variability effects on microstrip interconnects via Hermite polynomial chaos [C]∥2010 IEEE 19th Conference on Electrical Performance of Electronic Packaging and Systems. Piscataway, NJ, USA: IEEE Computer Society, 2011: 149-152.

[8] 吴烈, 杨仕友, 李玉玲. 基于多项式混沌和进化算法的快速鲁棒优化算法及其在电磁场逆问题中的应用 [J]. 中国电机工程学报, 2013, 33(3): 171-175. WU Lie, YANG Shiyou, LI Yuling. A fast robust optimization methodology based on polynomial chaos and evolutionary algorithm for inverse problems [J]. Proceedings of the CSEE, 2013, 33(3): 171-175.

[9] XIU D, KARNIADAKIS G E. Modeling uncertainty in flow simulations via generalized polynomial chaos [J]. Journal of Computational Physics, 2003, 187(1): 137-167.

[10]POZAR D M. 微波工程 [M]. 3版. 张肇仪, 周乐柱, 吴德明, 等译. 北京: 电子工业出版社, 2006: 42-43.

[11]PAUL C R. 多导体传输线分析 [M]. 杨晓宪, 郑涛, 译. 北京: 中国电力出版社, 2013: 145-147.

[12]MANFREDI P, GINSTE D V, DE Z D, et al. Frequency-and time-domain stochastic analysis of lossy and dispersive interconnects in a SPICE-like environment [C]∥21th Conference on Electrical Performance of Electronic Packaging and Systems. Piscataway, NJ, USA: IEEE, 2012: 65-68.

[13]KIRSCHNING M, JANSEN R H, Accurate wide-range design equations for the frequency-dependent characteristic of parallel coupled microstrip lines [J]. IEEE Transactions on Microwave Theory and Techniques, 1984, 32(1): 83-90.

[本刊相关文献链接]

张婧思,苗英恺,刘晓波,等.复杂电磁边界下基于曲线坐标的保角变换法.2016,50(2):43-47.[doi:10.7652/xjtuxb 201602008]

贾琦,黄斌科.粗糙导体表面提取印刷电路板介质参数的微分外推方法.2015,49(8):11-16.[doi:10.7652/xjtuxb2015 08003]

倪中非,黄斌科,师振盛.用于非规则波导传输特性分析的高效坐标变换法.2014,48(8):18-22.[doi:10.7652/xjtuxb 201408004]

赵重峰,黄斌科,师振盛.THz频段圆波导传输特性的特征方程分析法.2012,46(6):12-16.[doi:10.7652/xjtuxb2012 06003]

赵进全,尹建华,夏建生,等.一种非对称输电线路参数的在线测量方法.2016,50(2):80-84.[doi:10.7652/xjtuxb201602 014]

赵进全,张丹阳,李贺龙,等.非均匀耦合传输线瞬态响应灵敏度分析.2012,46(6):53-57.[doi:10.7652/xjtuxb201206 010]

王志国,梁志虎,刘纯亮.交流等离子体显示器改进型自适应子场编码驱动方法.2011,45(6):55-58.[doi:10.7652/xjtuxb201106010]

杨继波,李会勇,陈客松,等.球面共形天线阵列的稀布优化方法.2011,45(4):77-81.[doi:10.7652/xjtuxb201104014]

向坤,陈娟,张安学,等.提高喇叭天线增益的超介质构建方法.2011,45(2):92-96.[doi:10.7652/xjtuxb201102019]

黄斌科,胡红,宁曰民,等.分析表面粗糙有耗波导传输特性的频域有限差分方法.2009,43(10):85-88.[doi:10.7652/xjtuxb200910018]

(编辑 刘杨)

A Polynomial Chaos Expansion Method for Sensitivity Analysis of Microstrip Transmission Lines with Stochastic Parameters

CHENG Shi,HUANG Binke,SHI Zhensheng

(School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A method based on polynomial chaos (PC) expansion is proposed to calculate the response of transmission lines with uncertain parameters, such as variability in the substrate material and conductor geometry introduced in manufacturing processes. The stochastic per-unit-length lumped equivalent parameters of the transmission line, as well as the stochastic voltage and current responses for the transmission line, are expanded in terms of a series of orthogonal polynomial chaos basis functions, and all these stochastic variables are substituted into telegraph equations with random parameters. Then Galerkin’s method is used to transform the telegraph equations into a set of augmented equations with the expansion coefficients of voltage and current as variables. The expansion coefficients are then obtained by solving the augmented equations combined with source and load conditions. Moreover, the statistical properties, such as the means, variance and probability density distribution of the voltage and current responses and transfer functions, are obtained. Simulation results of the microstrip transmission lines show that the conductor width has a greater impact on the performance of the microstrip transmission line at lower frequencies, while the dielectric constant has a greater effect on transmission performance at higher frequencies. In addition, the computational cost of the proposed method is lower, and its simulation time is about 0.2% of the Monte Carlo method.

microstrip; telegraph equations; sensitivity; polynomial chaos expansion; Monte Carlo method

2016-04-27。 作者简介:程市(1992—),男,硕士生;黄斌科(通信作者),男,副教授。 基金项目:国家自然科学基金资助项目(61471293)。

时间:2016-10-26

10.7652/xjtuxb201612019

TN811.2

A

0253-987X(2016)12-0121-07

网络出版地址:http: ∥www.cnki.net/kcms/detail/61.1069.T.20161026.1751.002.html