混合因子矩阵分解推荐算法

赵长伟,彭勤科,张志勇

(1.西安交通大学电子与信息工程学院,710049,西安;2.河南科技大学信息工程学院,471023,河南洛阳)



混合因子矩阵分解推荐算法

赵长伟1,2,彭勤科1,张志勇2

(1.西安交通大学电子与信息工程学院,710049,西安;2.河南科技大学信息工程学院,471023,河南洛阳)

针对矩阵分解推荐算法在潜在属性与已知属性之间不能建立对应关系的问题,提出了一种混合显式属性与隐式属性的矩阵分解算法。该算法使用显式属性的相关性对因子矩阵进行约束,能够抑制稀疏数据矩阵分解中过拟合的问题,提高推荐精度,由于因子矩阵中包含显式属性,所以混合因子矩阵分解算法可以实现对新用户和新产品推荐,部分地解决了冷启动问题,实现了从评分数据到显式属性的映射,并对推荐结果给出一定的解释。在MovieLens数据集上的实验结果表明:相同因子数下,混合因子矩阵分解算法的推荐精度均优于偏置概率矩阵分解算法,并能够基于显式属性实现对新产品的推荐。

推荐算法;矩阵分解;混合因子;推荐解释;冷启动

在应用驱动下,个性化推荐系统得到了学术界和商业界共同的重视[1-3],推荐精度不断提高。矩阵分解(matrix factorization,MF)算法是个性化推荐中的经典算法。基本矩阵分解算法[4-5]将用户产品打分矩阵分解为用户潜在因子矩阵和产品潜在因子矩阵,用户对产品的打分预测值由用户潜在因子矩阵和产品潜在因子矩阵的内积求得。概率矩阵分解(probability matrix factorization,PMF)算法是应用较多的矩阵分解算法,在数据稀疏的情况下,PMF算法容易出现过拟合现象。为了防止数据过拟合,Netflix竞赛获胜者采用了正则化的矩阵分解算法(RSVD)[1],正则化能够提高整体打分预测的精度,在矩阵分解算法中被广泛采用。考虑到不同用户和产品具有不同打分偏置,Rendle等使用了偏置概率矩阵分解算法(BPMF)[6],该算法能够适应不同用户和产品的打分偏置,并有效地提高了打分预测的精度。PMF和BPMF算法仅考虑用户对产品的打分,并假定用户和产品的潜在属性是符合独立同分布的。含用户社交关系和产品属性相关性的矩阵分解算法[7-10]将用户社交关系和产品已知属性的相关性作为矩阵分解的约束,从而提高了整体的推荐精度和推荐项的覆盖率。在推荐结果解释方面,非负矩阵分解(NMF)算法[11]限定属性取值为非负,与属性的有无和权重值相对应,其结果具有一定的解释意义,但NMF算法没有给出潜在因子与显式属性的对应关系。针对矩阵分解算法的效率问题,Ortega等使用了群矩阵分解算法[12],但群矩阵分解算法本质上属于正则化算法。针对推荐数据稀疏的问题,Zhao等使用迁移学习的方法[13-14],融合不同领域的数据,解决了推荐系统数据稀疏的问题。

在传统的矩阵分解算法中,由于使用潜在属性因子,所以不能对推荐结果给出解释,也不能确定对特定用户推荐结果是否有改善。基于此,本文提出了一种结合显式属性和隐式属性的矩阵分解算法(hybrid matrix factorization,HMF)。HMF算法的创新点主要有3个方面:①在矩阵分解过程中,使用用户或产品之间显式属性的相关性对因子矩阵进行约束,防止稀疏数据矩阵分解中的过拟合问题;②利用HMF算法包含的用户和产品的显式属性,可以实现对新用户和新产品推荐,部分地解决了冷启动问题;③实现了打分矩阵到显式属性的映射,能够对推荐结果给出一定的解释。

1 混合矩阵分解算法

1.1 矩阵分解算法

对于m行n列的用户产品打分矩阵R,m为用户数,n为产品数,rij是矩阵R中第i行第j列的元素,表示第i个用户对第j个产品的打分。由于打分数据十分稀疏,R中存在大量的缺失数据。基本的矩阵分解算法在已知打分数据项上将打分矩阵R分解为m行k列的用户潜在属性因子矩阵U和n行k列的产品潜在属性因子矩阵V,其中k为潜在属性因子数(k≪m,n),并使UVT尽可能接近R。在基本矩阵分解算法中,由于使用了潜在属性因子,所以基本的矩阵分解算法不能给出推荐的解释。此外,该方法假定属性因子之间满足独立同分布条件,没有考虑用户和产品之间的关联关系对矩阵分解的影响。

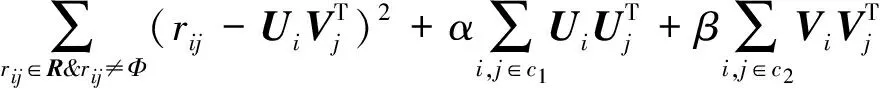
1.2 混合属性因子矩阵分解算法

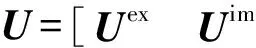
当产品因子矩阵中包含显式属性,用户因子矩阵采用隐式属性因子表示时,混合因子矩阵分解算法的代价函数定义为

(1)

混合因子矩阵分解算法通过优化如下目标函数实现

(2)

为了防止数据过拟合,对U、V进行正则化,相应的目标函数为

(3)

式中:λ为正则化系数。为了使矩阵分解结果具有解释性,限制产品因子属性值为非负值,目标函数为

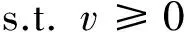
(4)

式中:v∈V为产品因子属性的值。

1.3 问题求解

随机梯度下降算法(stochastic gradient descent,SGD)和交替最小二乘法(alternating least squares,ALS)是矩阵分解中最常用的算法。本文使用改进的随机梯度下降算法对因子矩阵进行求解。首先使用代价函数对Ui和Vj求偏导,有

(5)

(6)

2 推荐解释与冷启动

在传统的矩阵分解算法中,由于分解的矩阵使用潜在属性因子,所以不能对推荐结果给出解释,也不能推荐新产品和新用户,即面临冷启动问题。在混合因子矩阵分解算法中,由于包含了用户或产品的显式属性,所以能够给出推荐解释并能一定程度地解决冷启动问题。

将用户潜在属性因子矩阵U分为与产品显式属性特征对应的块Uex′和与产品隐式属性特征对应的块Uim′,则显式属性的打分权重为

(7)

显式属性所对应的权值表示了用户对产品已知属性的偏好程度,进一步,可以使用该权值对推荐结果给出相应的解释。对于已知属性的新产品,当wrij大于一定阈值时,可以依据产品的已知属性向用户推荐新产品。

针对冷启动问题,考虑对产品因子矩阵采用显式属性表示,在产品因子属性已知的基础上,使用式(8)计算用户因子矩阵的值。

(8)

这种情况下,用户i对已知属性产品j的打分预测值为

(9)

与产品矩阵表示相似,当用户矩阵使用混合属性因子表示时,可以实现向新用户推荐产品项。

3 实验结果及分析

3.1 数据集

实验使用了MovieLens数据集[15],MovieLens数据集由3个不同大小数据集构成,其中100 kB的数据集中包含943个用户对1 682部电影的100 000条评分数据,评分等级为1到5,共5个等级,等级1到5反映了用户对该电影的偏好程度。每个用户至少对20部电影进行了评分。每一条评分数据包含用户、电影、评分级评分时间信息,该数据集还包含简单的用户人口学统计信息和电影的体裁类型信息。

3.2 打分预测精度

推荐系统有多种评价指标,打分预测精度常用的评价指标有绝对误差Em和均方误差Er

(10)

(11)

式中:T为测试集,|T|表示测试集样本的数目。均方误差Er对预测误差较大的值更敏感。

实验中对不同潜在属性因子数和混合因子数的推荐算法的预测精度进行了比较,实验结果采用5折交叉验证的方法。

图1、图2给出了BPMF算法在不同因子数k下打分预测精度Em和Er变化的情况。实验中仅使用了用户对产品的打分信息,正则化系数λ设置为0.02,学习率α设置为0.1。用户和产品矩阵因子均为潜在属性因子。

图1 潜在因子数与绝对误差的关系

图2 潜在因子数与均方误差的关系

由图1、图2可以看出,在因子数k值小于确定值的情况下,潜在因子矩阵分解算法打分预测精度随k值的增加而增加。为了验证结合显式属性的矩阵分解HMF算法的有效性,分别对总因子数固定和显式属性因子数固定的情况进行了实验。表1给出了总因子数固定为5的情况下,含不同数目显式因子的HMF算法的预测精度。实验中正则化系数λ设置为0.02,学习率α设置为0.1,显式属性因子值固定为0.2。实验中显式因子来自电影体裁信息,在MovieLens数据集中,包含了19种不同类型的体裁信息,但属于某些体裁数的电影非常少,这些体裁属性在预测精度中没有普遍性。实验中按照不同体裁的电影数对体裁属性进行排序,得到一个体裁属性排序列表。在HMF算法中,显式属性数为n时,对应的为体裁属性排序列表的top-n项的属性。在表1中,当显式属性数为5时,电影矩阵V中仅包含显式属性。

由表1可以看出,当包含两个显式因子时,绝对误差最小为0.731 6。与BPMF算法相比,其预测精度有较大的提高,这是因为HMF算法中结合了显式因子,增加了显式属性的相关约束。同时,该方法中包含了隐式属性,隐式属性能够表示用户偏好和产品属性中难以显式表示的偏好信息。随着显式因子数的增加,显式属性相关性约束增加,隐式属性表示的推荐相关的潜在因子被削弱,导致推荐精度降低。

表2中给出了显式因子数固定为5,总因子数变化范围为5到30时,HMF算法的打分预测精度。

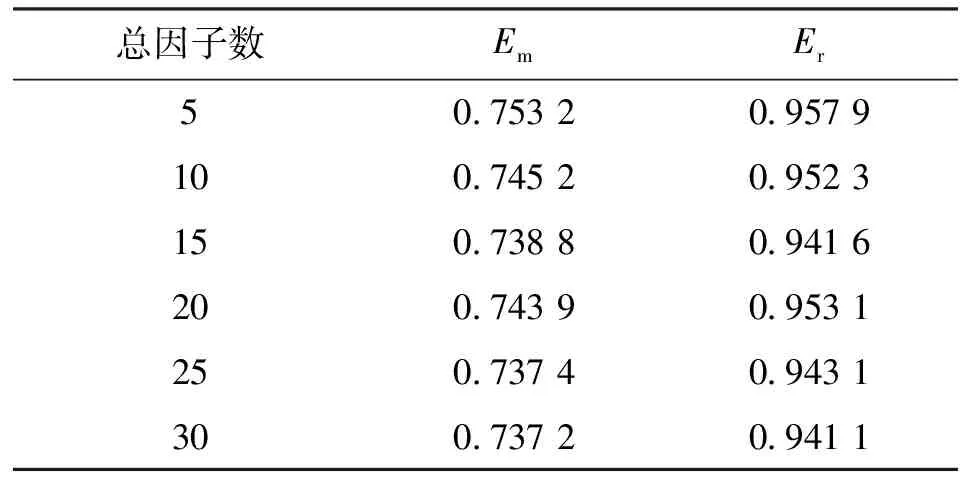
表2 固定显式因子数时HMF算法的预测精度

由表2可以看出,在显式属性因子数固定的情况下,HMF算法的打分预测精度与显式属性因子数占比有一定的关系。在因子数为15时,HMF算法取得较好的结果,显式属性对因子矩阵的相关关系给出了较好的约束。随着因子数的增加,显式属性在全部因子数中的比例降低,相关性约束减小,与BPMF算法相比,HMF算法对推荐精度提高十分有限。

3.3 冷启动和推荐解释

在个性化推荐系统中,传统的MF方法不能推荐新产品和新用户的原因是用户偏好和产品属性均采用潜在属性因子表示,用户偏好和产品属性不能明确表示。HMF算法中,当产品项使用含有显式属性因子矩阵表示时,与其对应的用户因子项可看作用户对该属性的偏好。HMF算法能够基于用户的偏好和产品显式属性推荐新的产品。

表3给出了MovieLens数据集中使用电影体裁类型作为显式属性时,HMF算法和基于产品属性相似度算法在新产品项上的推荐精度。实验中HMF和基于产品属性相似度算法均使用了电影体裁项中前5个包含电影数较多的属性项。

由表3可以看出,在新产品推荐上,HMF算法的精度远高于基于产品属性推荐方法的精度,这是因为HMF算法能够区分用户对产品不同属性项偏好的权重,而基于产品属性的推荐方法对属性的权重不做区分。

表3 HMF算法和Item-based算法新产品推荐精度

由于HMF算法包含显式属性,该方法也能够对推荐结果给出一定的解释。具有推荐解释功能使推荐结果更容易被用户接受。与产品推荐类似,当用户矩阵含有显式属性时,HMF算法可以实现对新用户的推荐和推荐解释。

4 结 论

本文提出了一种混合因子矩阵分解HMF算法,HMF算法的因子矩阵中包含显式属性和隐式属性。与基本的矩阵分解算法相比,HMF算法使用了显式属性之间的相关性,对稀疏数据矩阵分解给出了合理的约束,提高了推荐精度。同样,由于使用了显式属性因子,HMF算法能够推荐新产品并对推荐结果给出一定的解释。本文中显式属性仅使用了电影体裁属性,没有考虑其他显式属性和显式属性选取的问题,下一步,将对显式属性选取进行研究,对用户偏好的深层次原因进行分析,进一步提高推荐系统的推荐精度和推荐解释的能力。

[1] KOREN Y, BELL R, VOLINSKY C. Matrix factorization techniques for recommender systems [J]. Computer, 2009, 42(8): 30-37.

[2] MA W, FENG X, WANG S, et al. Personalized recommendation based on heat bidirectional transfer [J]. Physica: A Statistical Mechanics and Its Applications, 2016, 444: 713-721.

[3] RICCI F, ROKACH L, SHAPIRA B. Recommender systems handbook [M]. 3rd ed. Berlin, Germany: Springer, 2010: 1-35.

[4] SALAKHUTDINOV R, MNIH A. Probabilistic matrix factorization [C]∥Proceedings of the 2015 Advances in Neural Information Processing Systems. Cambridge, MA, USA: MIT Press, 2015: 1257-1264.

[5] SALAKHUTDINOV R, MNIH A. Bayesian probabilistic matrix factorization using Markov chain Monte Carlo [C]∥Proceedings of the International Conference on Machine Learning. New York, USA: ACM, 2008: 880-887.

[6] RENDLE S, SCHMIDT-THIEME L. Online-updating regularized kernel matrix factorization models for large-scale recommender systems [C]∥Proceedings of the 2008 ACM Conference on Recommender Systems. New York, USA: ACM, 2008: 251-258.

[7] 秦继伟, 郑庆华, 郑德立, 等. 结合评分和信任的协同推荐算法 [J]. 西安交通大学学报, 2013, 47(4): 100-104. QIN Jiwei, ZHENG Qinghua, ZHENG Deli, et al. A collaborative recommendation algorithm based on ratings and trust [J]. Journal of Xi’an Jiaotong University, 2013, 47(4): 100-104.

[8] 郭磊, 马军, 陈竹敏, 等. 一种结合推荐对象间关联关系的社会化推荐算法 [J]. 计算机学报, 2014, 37(1): 219-228. GUO Lei, MA Jun, CHEN Zhumin, et al. Incorporating item relations for social recommendation [J]. Chinese Journal of Computer, 2014, 37(1): 219-228.

[9] MA H, KING I, LYU M R. Learning to recommend with explicit and implicit social relations [J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 135-136.

[10]MA H, KING I, LYU M R, et al. SoRec: social recommendation using probabilistic matrix factorization [C]∥Proceedings of the 2008 ACM Conference on Information and Knowledge Management. New York, USA: ACM, 2008: 931-940.

[11]LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization [J]. Nature, 1999, 401(6755): 788-791.

[12]ORTEGA F, HERNANDO A, BOBADILLA J, et al. Recommending items to group of users using matrix factorization based collaborative filtering [J]. Information Sciences, 2016, 345: 313-324.

[13]ZHAO L, PAN S J, XIANG E W, et al. Active transfer learning for cross-system recommendation [C]∥Proceedings of the 27th AAAI Conference on Artificial Intelligence. Palo Alto, CA, USA: AAAI Press, 2013: 1205-1211.

[14]JIANG M, CUI P, WANG F, et al. Social recommendation across multiple relational domains [C]∥Proceedings of the ACM International Conference on Information and Knowledge Management. New York, USA: ACM, 2012: 1422-1431.

[15]HARPER F M, KONSTAN J A. The movielens datasets: history and context [J]. ACM Transactions on Interactive Intelligent Systems, 2015, 5(4): 1068-1074.

(编辑 武红江)

A Matrix Factorization Algorithm with Hybrid Implicit and Explicit Attributes for Recommender Systems

ZHAO Changwei1,2,PENG Qinke1,ZHANG Zhiyong2

(1. School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. School of Information and Engineering, Henan University of Science and Technology, Luoyang, Henan 471023, China)

A novel hybrid matrix factorization algorithm (HMF) is proposed to solve the problem that the correlation between latent factors and explicit attributes can not be established in traditional matrix factorization methods. The algorithm combines implicit and explicit attributes and uses correlations among explicit attributes to constrain factor matrixes, and to relieve the over fitting in sparse data matrix decomposition. Since factor matrixes include explicit attributes, HMF is used to solve the problem of cold start and to recommend new items. HMF realizes mapping from rating matrix to weights of explicit attributes and offers an interpretation for recommender items. Experiment on MovieLens datasets shows that the accuracy of HMF is superior to that of BPMF for same number of factors, and HMF can be used to recommend new items based on explicit attributes.

recommender algorithm; matrix factorization; hybrid factor; recommended interpretation; cold start

2016-05-30。 作者简介:赵长伟(1971—),男,博士生;彭勤科(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61370220);河南省高校科技创新团队支持计划资助项目(15IRTSTHN010)。

时间:2016-10-19

10.7652/xjtuxb201612014

TP393;G558

A

0253-987X(2016)12-0087-05

网络出版地址:http: ∥www.cnki.net/kcms/detail/61.1069.T.20161019.1622.010.html