初中学生数学解题中的盲区分析和解决办法

广东省佛山市南海西樵中学(528211)何少华

初中学生数学解题中的盲区分析和解决办法

广东省佛山市南海西樵中学(528211)何少华

汉语词典中的盲区是指雷达、胃镜等探测或照射不到的地方;比喻及不到或认识不清的方面或领域.盲区的种类繁多有驾驶盲区、法律盲区、建筑盲区、管理盲区等等.盲区这个词在我心目中的理解就是看不到或者被忽略的地方.汶川大地震的救援工作中,因为搜救人员细心搜寻那些救援中的盲点,才能夺取救灾、减灾的全面胜利.司机师傅避免后视镜的盲区,才能使行驶安全.人们避免人体七个容易被忽略保湿的盲区,才能使人容光焕发.通过以上的一些生活例子,我们不难发现,如果我们能克服或避免盲区,问题就不成问题了.

同样,我们的学生在解决问题时,出现错误或者不懂解决问题,往往不是他们没有学过这些知识,而是对知识熟视无堵,存在知识盲区.如果我们的学生能够克服盲区或避免盲区或减少盲区,问题解决就会畅通无阻.通过观察发现学生在解决问题上存在的盲区,我大概分成五类以及采取了相应的解决方法.

一、知识结构型的盲区

这种现象往往出现在几何图形知识应用中,因为每个图形有它繁杂的性质,学生运用起来不知从何用起,也就是存在知识的盲区.譬如:直角三角形,学生学习了直角三角形,它的学习是一个螺旋式上升的过程,由浅入深,由具体到抽象,先单调应用两锐角互余,后来发展到抽象的三角函数,学生由应付自如,转化为不知从何入手.其实这些问题从哪入手都基本行得通,路径是很多的.关键是学生能否找到一些简便的路子,不以至耗时多,有时还未能最终达到目的.此时我们应该让学生懂得自己进行知识的积累和概括(或教会学生如何进行知识的概括和积累).

图1

学生只有通过对知识建构梳理,全面了解知识的地位与作用,知识的盲区才可能减少,甚至可能避免了知识的盲区.

例如1:九年级上册P12页定理的证明,如果学生没有造成对“直角三角形斜边上的中线等于斜边的一半”产生盲区,那么这个定理的证明就不会像书中构造三角形全等,而是采用取斜边的中点作出直角三角形斜边上的中线构造出等边三角形推出直角三角形的一个锐角等于60℃,从而推出另一个锐角等于30℃,把问题轻松解决了.除此之外还有线段的垂直平分线和角平分线的判定定理的使用,也是因为平时少用,或先入为主,造成知识的盲区,使学生思维局限,取不到好的效果.因此学生进行知识结构的认识和整理是应该的,往往会使处理的问题事半功倍.

二、忽略型的盲区

造成忽略型的盲区与学生的阅读的能力有关.现在的学校虽然很重视学生的阅读,并且专门开辟了语文阅读课.学生虽然有了时间阅读,但形式局限,所看的刊物也局限,只对学生的写作能力(见多是广)起到有所提高的作用,而对学生的数学阅读审题,提取信息作用效果不明显,学生在解决数学问题时往往就出现盲区.因此我们还是要结合数学的特点,采取一些相应的办法提高阅读能力.学生出现忽略型(忽视型)的盲区,我觉得主要在对一些概念的应用,以及一些阅读量较大(题目详细,条件多)的题目中出现.

例如2:关于x的方程(a−2)xa2−2+ax+b=0是一元二次方程的条件是____.

学生解决此问题时会出现忽略a−2̸≠0这个条件.那么我们可以让学生在解决这个问题时,通过阅读把问题中的关键词或关键句编成条件①②③,每个条件推出一个结果,综合结果便得出正确结论,就不会忽略此条件.除此之外,还有分式的值为0的条件____等等.

另外考试结束,通常有些学生会抱怨题目长文字多,不知题目讲什么.甚至有些学生一看这些题目,已经出现了挡之于门外的心理.解决这些问题往往不理想,绝大部分学生就是差那么一点点.究其原因是学生对题目中的一些条件忽视了.那么,遇到这种情况,我觉得应引导学生把题目的条件分层.

例如3:天气热了,吃冰棒的感觉真好,小明想自制甲乙两种冰棒共50根,于是分别买了A、B两种必需的原料各400克、300克,并知一根甲种冰棒分别需A种原料10克,B种原料3克;一根乙种冰棒分别需A种原料6克,B种原料8克;

1)设自制甲种冰棒x根,根据题中的情景列出不等式组,求出x的取值范围.

2)自制一根甲种冰棒需成本0.4元,一根乙种冰棒需成本0.3元,请写出这50根冰棒成本纵额y(元)与甲种冰棒x(根)的函数关系.又知甲、乙两种冰棒在市场上的批发价每根都是0.6元,根据第(1)问的结果自制这50根冰棒与批发价相比最多能节约多少钱?

我们关键解决第一问,那么在分析问题的时候能把数据分为三层,便可以清晰了解题意.

图2

第三层:甲冰棒用A种原料+乙冰棒用A种原料6 400g

甲冰棒用B种原料+乙冰棒用B种原料6 300g

在课堂教学上,老师能重视把此类问题进行“分层”教学,并培养学生若能这样分析问题,要求学生养成此类问题的分析习惯,多长的问题,多么复杂的问题,只要分层列条件,每层条件的用途就显而易见,就不会因条件多而忽视条件解不了,更不会眼花缭乱无处寻.

三、生活知识型盲区

现在的学生所接触的东西多,知识的领域也广了,能力也强了(操控电脑,弹奏乐器等等),但唯独有一样能力是缺乏的,就是生活认识能力.当问题结合一些生活实际的东西时,学生的认知就出现不同程度的空白.譬如:在我们初二的下学期学习的不等式应用中所提到的运输问题,学生就出现因生活知识出现盲区导致不会解决问题.

例如4:荣昌公司将100吨货物运往某地销售,经与春晨运输公司协商,计划租用甲、乙两种型号的汽车共6台,用这6辆汽车一次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨,已知租用1辆甲型汽车和2辆乙型汽车共需要2500元;租用2辆甲型汽车和1辆乙型汽车共需要2450元;且同一种型号汽车费用相同.

(1)求租用一辆甲型汽车,一辆乙型汽车的费用分别是多少?

(2)若荣昌公司此次租用车费不超过5000元,该公司有几种租车方案,并求最低的租车费.

学生在解决第二问时,一部分学生忽略了100吨这个条件;一部分学生不具备运输的常识,安排运输载重量只预留空(或刚好),不会出现不够装(不够坐).因此如果设甲型为a辆,则乙型为(6−a)辆,不但列出800a+850(6−a)6 5000,还要列出16a+18(6−a)≥100这两个不等式组成不等式组才能解决问题.我们在教学中,让学生尽量了解实际,感受生活,融入生活,掌握生活常识,避免生活常识的盲区,才能更好的解决问题.

四、“请君入瓮型”盲区

学生解决问题时,有时会出现走进了自设的框框当中,走不出来;检查时却发现路径没有错误,但又原因不明,陷入困境,这可谓请君入瓮型.这些问题往往出现在因式分解的应用中和方程应用中.学生通常在“设”过程中考虑不周所致.

例如5:上课时,老师提出了一个问题:“连续两个奇数的平方差,结果是怎样的数?”请解答这个问题.

学生往往设连续两个奇数分别为n、n+2,依题意得:

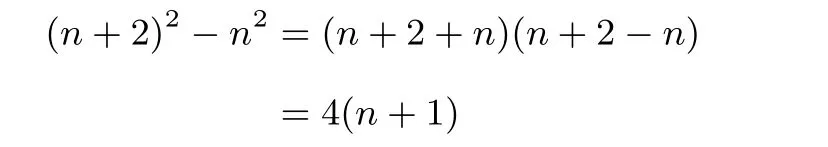
出现误判连续两个奇数的平方差,结果是4的倍数.如果平时让学生养成连续两个奇数设成2n+1、2n–1,依题意得:

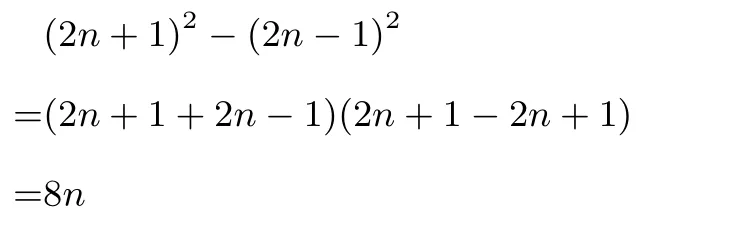
连续两个奇数的平方差,结果是8的倍数便顺理成章.出现两种差异主要是学生不当的设未知数,引进了一个不明身份的量,而学生没有发现n+1其实是一个偶数,是2的倍数.另外,还有我们九年级一元二次方程中的销售问题究竟采用间接设还是直接设,老师在讲课时应该引导学生.讲明设的重要性.学生才不会请君入瓮.

五、综合应用型盲区

综合应用在考试中起到选拔人才的作用,它所触及的知识广,提取知识的灵活度大.我们的学生接触这类问题的困难在于相关的信息提取不出来,知识网中存在盲点,知识网间存在盲区.此外,我们的学生大多都只懂得仿造,先入为主.譬如:例4中的第一问,一部分学生就没有想到用二元一次方程组解决.因为不等式的应用问题,招牌式—不等式组解决.还有例3中的第二问,就应该结合一次函数来解决问题.让学生知道不等式应用有时与方程有联系,与函数也有联系.知识不再单调唯一,而是多元化.我们的教学不要只着眼于教会学生一道题,或解决一类题.要引导学生如何切入问题,找问题的相关的多个支点,还要教会学生善于积累,如何积累,运用积累等等.尽量把网中的盲点扫除,把盲区范围缩少.这样学生解决综合问题的能力应该会提高.

学生出现学习性的差异,关键在于他们对这个知识认识的盲区大少或多少,作为老师在授课中考虑这个问题,相信学生不会因为知识的盲区以影响解决问题的能力.