全空间中粒子和裂纹的对偶边界积分方程及数值解

马杭,潘蒙

(1.上海大学理学院,上海　200444；

2.上海大学上海市应用数学和力学研究所,上海　200072)

全空间中粒子和裂纹的对偶边界积分方程及数值解

马杭1,潘蒙2

(1.上海大学理学院,上海200444；

2.上海大学上海市应用数学和力学研究所,上海200072)

针对弹性固体中同时含有粒子和裂纹的情况,建立了全空间中的粒子和裂纹的位移间断形式的对偶边界积分方程计算模型,解决了全空间条件下难以对研究对象进行直接加载的问题.采用边界积分方程的离散形式对含有少量粒子和裂纹的典型情况进行了数值分析,其中对粒子边界(或界面)和裂纹面分别采用边界点法和高斯配点法进行离散,计算了裂纹的应力强度因子,探讨了粒子与裂纹的相互作用.通过与已有研究结果比较,验证了计算模型与计算机程序的正确性与可靠性.

粒子；裂纹；对偶边界积分方程；数值解；应力强度因子

弹性固体中不可避免地含有某些缺陷,例如裂纹和粒子.弹性固体中的粒子可以是夹杂物或者局部析出相,也可以是人工加入的增强相,例如粒子增强复合材料.含有缺陷的弹性固体属于非均质问题.含有裂纹和粒子等缺陷使得弹性固体的性能发生改变,这使其成为固体力学研究人员和材料工程师所关注的焦点之一.另外,对全空间中粒子和裂纹弹性状态的研究往往是进一步研究的基础和参照基准,因此具有重要的意义.

在线弹性断裂力学的研究中,有两类相辅相成的研究方法,即解析方法和数值方法.多年来通过两类方法都取得了大量的研究成果.解析方法适于裂纹构型相对简单的情况,数值方法则适于分析比较复杂的情况.在各种数值方法中,基于边界积分方程的数值方法表现出更大的优越性,这已逐渐成为研究者的共识[1-2].在含有裂纹的问题中,由于裂纹的两个面在几何上是完全重合的,如果仅仅使用一个边界积分方程,必须采用特殊的手段,例如采用分域法将裂纹置于问题的边界,否则将导致问题的退化而不可解[3].具体而言,退化问题经过离散后得到的系统方程的系数矩阵是奇异的,因而不可解.采用对偶边界积分方程,即通过位移边界积分方程和面力边界积分方程来共同描述含有裂纹的问题,就能够避免问题的退化,因此成为边界积分方程解决裂纹问题的主要方法.

关于裂纹问题已有大量研究成果,例如各种条件下裂纹之间的相互作用、裂纹与孔洞的相互作用等[4-7].Dong等[8-13]较早地研究了裂纹与粒子间相互作用,首先提出了积分方程方法,其中粒子用区域积分描述,需要在粒子上剖分内部胞元；继而提出了边界积分方程方法,并对原有算法进行改进,研究了各向异性、横观各向同性条件下裂纹与粒子的相互作用问题以及材料中刚性线的影响.采用边界积分方程方法只需在界面上剖分单元,但总体而言,采用该方法对裂纹与粒子间的相互作用进行研究的成果相对较少.本工作中的粒子是指广义的粒子,其弹性模量可以大于或小于基体的弹性模量,如果将粒子的弹性模量设为零,则粒子退化为孔洞,在这个意义上,本工作的研究具有一般性.本工作的长远目标是研究大规模问题的计算方法以作为进一步研究的基础,因此需要在全空间中研究粒子和裂纹的弹性状态.由于全空间不存在外边界,其加载条件有一定的特殊性,在全空间中无法对所研究的对象按有限物体那样直接进行加载.因此在前人[14]工作的基础上,首先建立了全空间中粒子和裂纹的位移间断形式的对偶边界积分方程计算模型,解决加载问题；然后采用边界积分方程的离散形式——边界点法[15]对含有少量粒子和裂纹的典型情况进行数值分析,计算裂纹的应力强度因子,探讨粒子与裂纹的相互作用；最后通过与已有研究结果进行比较,对计算模型与计算机程序的正确性与可靠性进行验证.

1　计算模型与求解

1.1边界积分方程

对于区域为Ω,边界为Γ的各向同性弹性体,位移和面力的边界积分方程[1]分别为

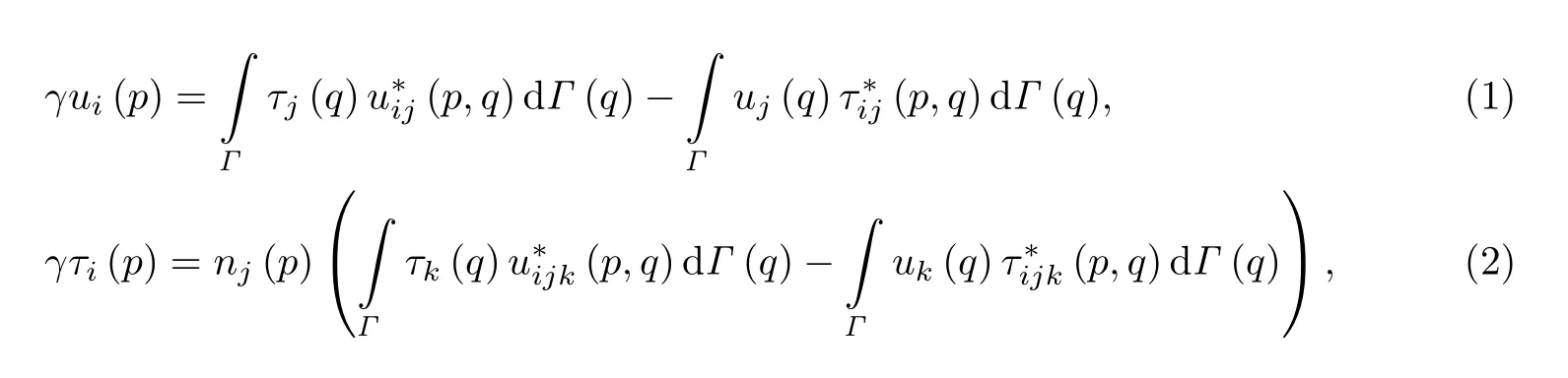
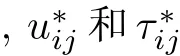
1.2区域的分解与加载

图1　全空间中受远场单位拉伸载荷的粒子和裂纹Fig.1　Particle and crack under far field unit tension in full space

1.3矩阵形式的边界积分方程

图2中分离的粒子可用式(1)描述.离散后的式(1)可写成以下矩阵形式：

图2　分离的粒子与全空间中的孔洞和裂纹Fig.2　Separated particle and the hole and crack in full space

图3　受远场拉伸的均质全空间与不受远场载荷的孔洞和裂纹Fig.3　Full uniform space under far-field tension and the hole and crack without far-field load

对于全空间中的孔洞和裂纹(见图3),可用位移间断的对偶边界积分方程(3)和(4)来描述.当源点p位于孔洞边界(或粒子边界)时采用式(3)描述,而当源点p位于裂纹表面时则采用式(4)描述.离散后的矩阵形式为

式中,R为右向量,是已知量,即

利用式(8)求得粒子界面的位移u和裂纹张开位移δ,再利用式(6)求出粒子边界的面力τ.分别记基体与粒子的弹性模量为E和EI,定义模量比为假设基体与粒子的泊松比相同,则存在如下关系：

利用式(11)和(12)可使计算得到一定程度的简化.

如果粒子的弹性模量为0,即β=0,则粒子和裂纹的问题退化为孔洞和裂纹的问题,孔洞边界上的面力为0.这时,式(12)不成立,式(8)退化为

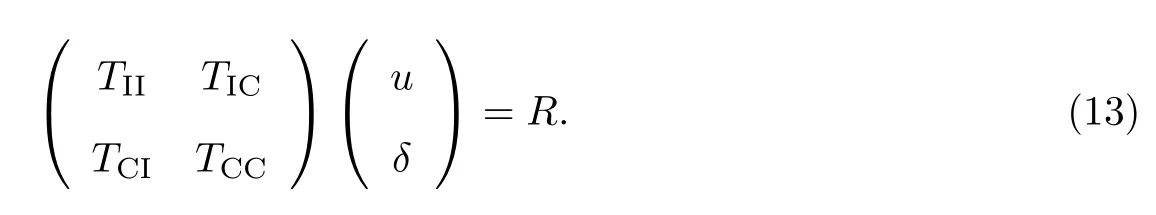
1.4离散方式与应力强度因子的计算

采用边界积分方程的两种离散形式分别对粒子边界和裂纹表面进行离散,其中粒子边界的离散采用了边界点法[15].设N为粒子边界的节点数,对于只有一个粒子的情况,列向量u, τ的大小为d·N,系数矩阵TII,UII的大小为(d·N)2,其中d为维数.如果粒子总数为NI,则列向量u,τ的大小为d·NI·N,矩阵TII,UII的大小为(d·NI·N)2.

对裂纹表面采用高斯配点法进行离散[6,16].当源点和场点均位于同一裂纹的上表面时,式(4)转化为

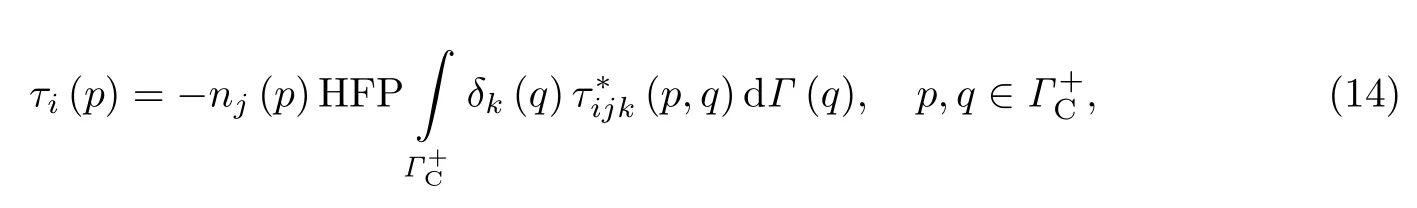
式中,HFP表示Hadamard主值积分[17].利用积分核τ∗ijk的具体表达式,可将式(14)简化为

式中,µ为剪切模量,ν为泊松比,r为源点和场点间的距离.式(15)表明在二维条件下,张开型和滑开型位移间断与相应的面力(即裂纹的法向面力和切向面力)具有完全相同的对应关系.记NG为裂纹表面的高斯配点数,对于单位长度的裂纹,即设裂纹半长为a=1,则式(15)的离散形式可写为

式中,ξk和wk分别为高斯点的位置和权.式(7)和(8)中的系数矩阵TCC可用式(16)计算得到.式(16)中含有裂纹张开位移δ(δ1δ2)的导数,为了便于计算,沿裂纹面对其进行Lagrange插值：

式中,lk为NG+2阶Lagrange函数,满足关系式δ(−a)=δ(+a)=0.设裂纹总数为NC,则列向量δ的大小为d·NC·NG,系数矩阵TCC的大小为(d·NC·NG)2.

需要指出的是,通常裂纹面上的实际面力为0,式(14)～(16)中的面力可理解为虚拟面力[6],由于粒子对裂纹存在影响,裂纹面上的虚拟面力并不等于τ0C(见图3).式(14)～(16)表明裂纹张开位移与虚拟面力存在特定的关系,利用这个关系可更方便地计算应力强度因子,避免使用裂纹尖端附近某个位置上的位移或应力值.具体而言,当问题求解之后,首先利用式(16)由裂纹张开位移求高斯节点上的虚拟面力,然后将求得的面力用下列多项式拟合,即

式中,ci为多项式待定系数,NP为多项式的阶数.求得待定系数ci后,代入下式：

便可得到计算应力强度因子的公式如下：

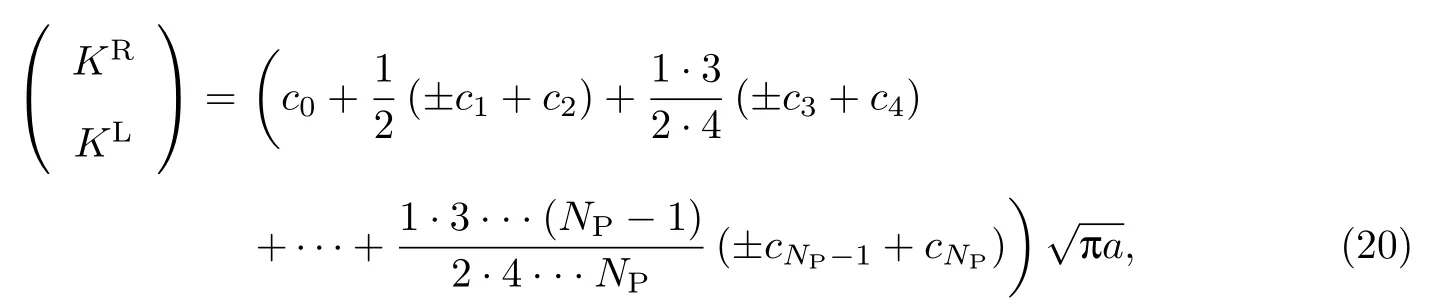
式中,KL和KR分别表示裂纹左端和右端的应力强度因子.事实上,这种计算应力强度因子的方法充分利用了裂纹的整体信息,即裂纹张开位移和虚拟面力,从而使得应力强度因子的计算结果更为精确和稳定.

2　算例

如前所述,本工作的算例中采用边界积分方程的两种离散形式分别对粒子边界和裂纹表面进行离散,其中对粒子边界的离散采用了边界点法,N为粒子边界的节点数；对裂纹表面采用高斯配点法进行离散,NG为裂纹表面的高斯配点数.

2.1裂纹与双孔

首先考虑裂纹与双孔问题(见图4),目的是校核计算机程序.由于该算例的几何构型与加载条件具有对称性,裂纹两端的应力强度因子(stress intensity factor,SIF)的值相同,而且滑开型(Ⅱ型)的应力强度因子为0,因此只需计算张开型(Ⅰ型)的应力强度因子.

对于图4(a)中的情形,令

其中裂纹的无量纲应力强度因子

图4　裂纹与双孔Fig.4　Crack and two holes

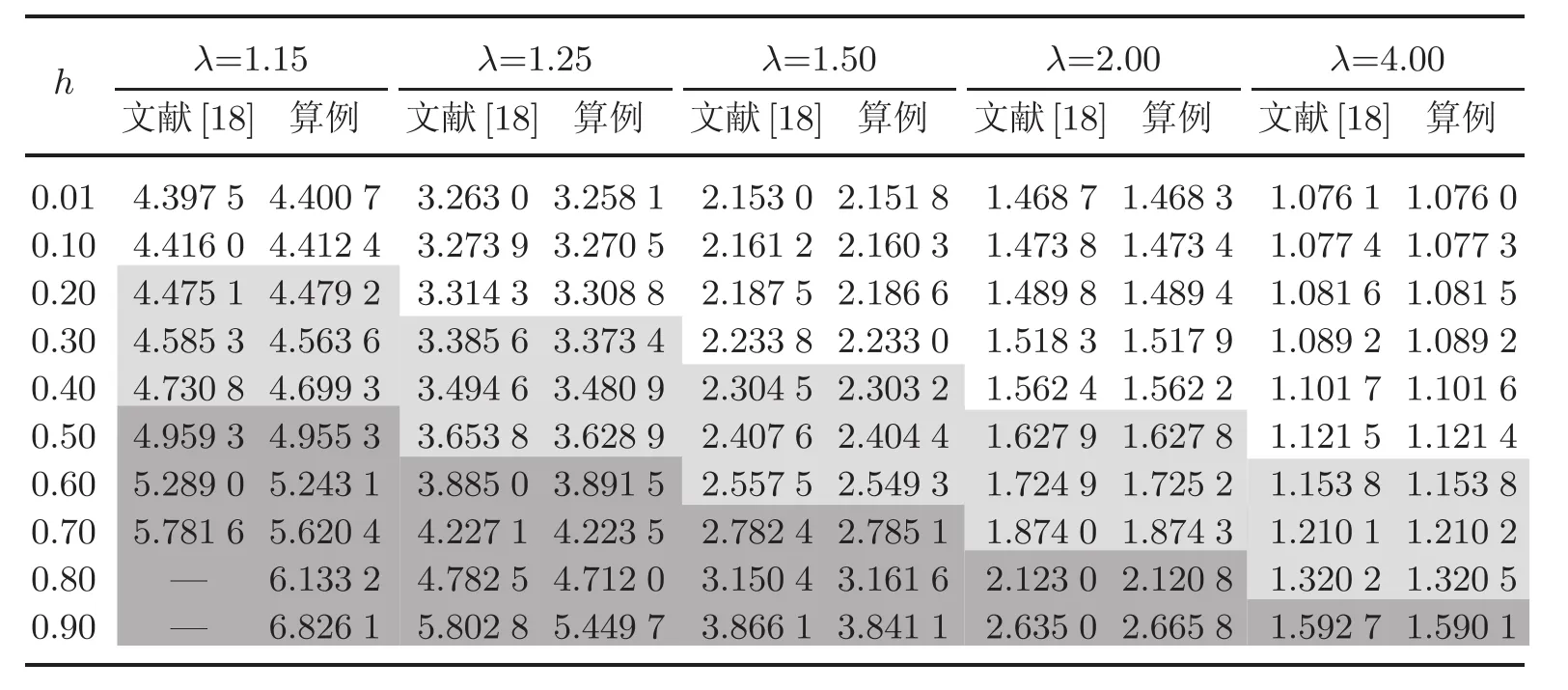
表1　纵向加载情况下裂纹的无量纲应力强度因子Table 1　Dimensionless SIF of the crack for longitudinal load

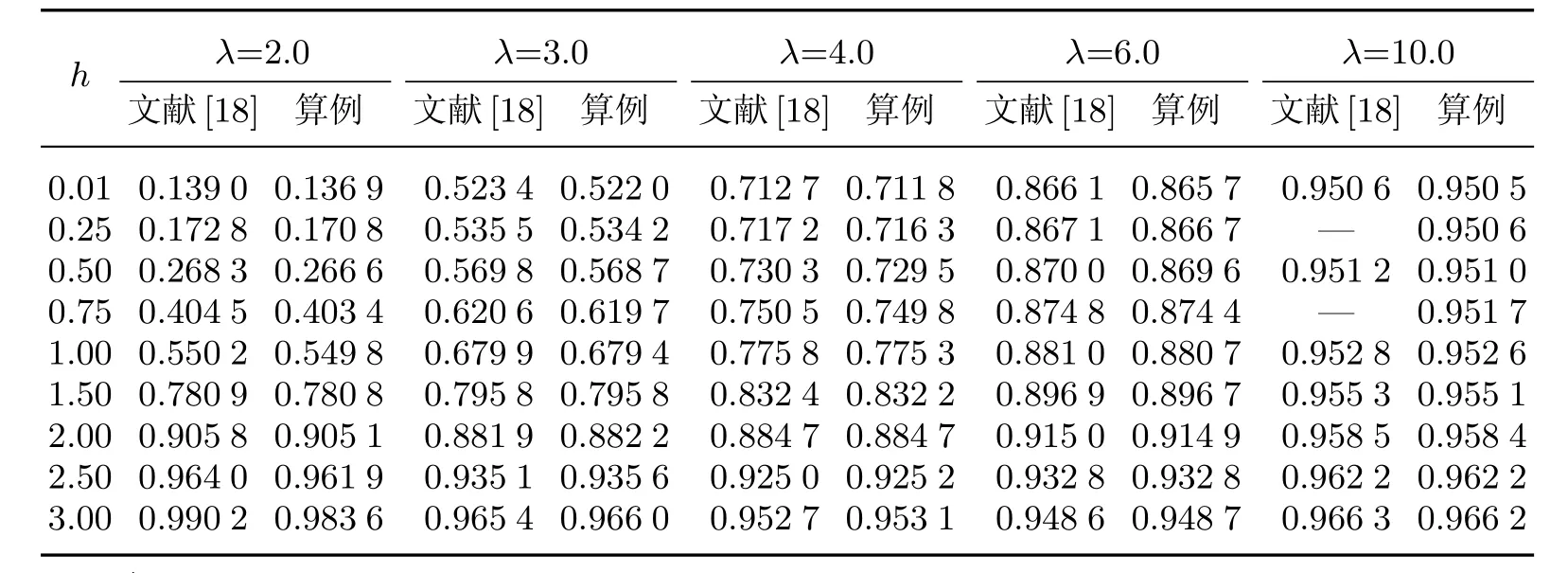
表2　水平加载情况下裂纹的无量纲应力强度因子Table 2　Dimensionless SIF of the crack for horizontal load

2.2裂纹与粒子的方位

考察两种情况下裂纹与各种不同硬度粒子的方位变化对应力强度因子的影响,结果如图5所示.第一种情况为粒子方位变化时裂纹保持水平位置不变(见图5(a)),第二种情况为粒子方位变化时裂纹的方向同步变化(见图5(b)).粒子的硬度,即模量比的变化范围从0到100.对裂纹面和粒子界面分别采用NG=15和N=40个节点进行了离散.计算结果如图6～9所示.

图5　裂纹与粒子的方位Fig.5　Positions between crack and particle

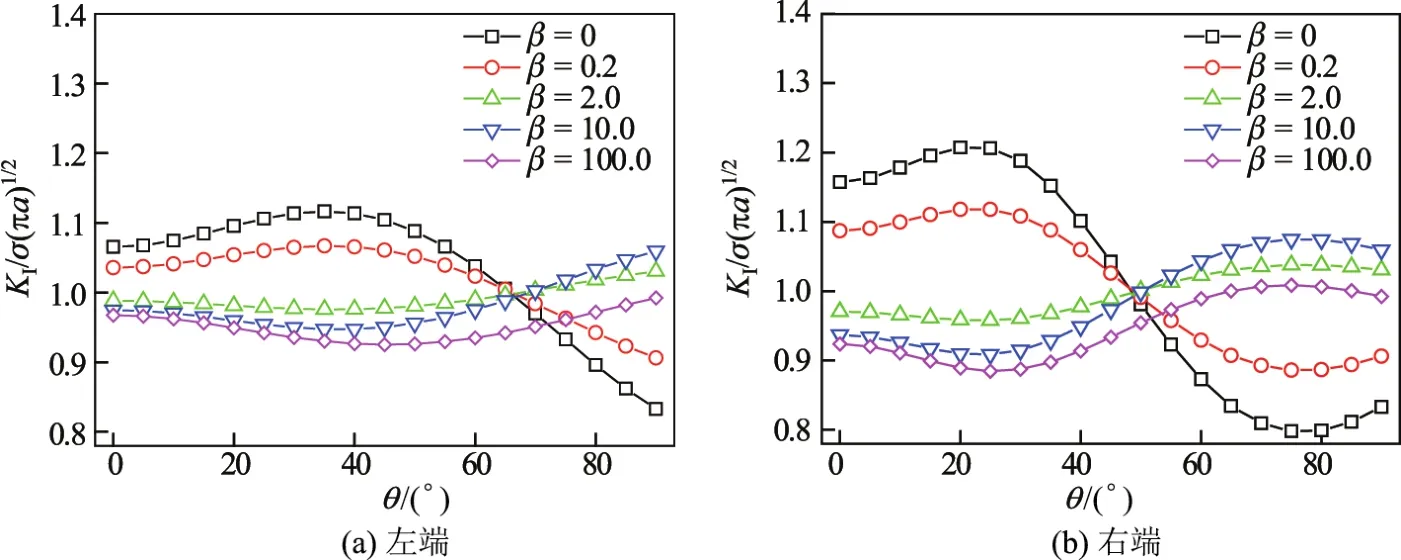
图6　裂纹左端和右端Ⅰ型应力强度因子与粒子方位角的关系(水平裂纹)Fig.6　TypeⅠSIF at left tip and right tip of crack as a function of particle bearing angle (horizontal crack)

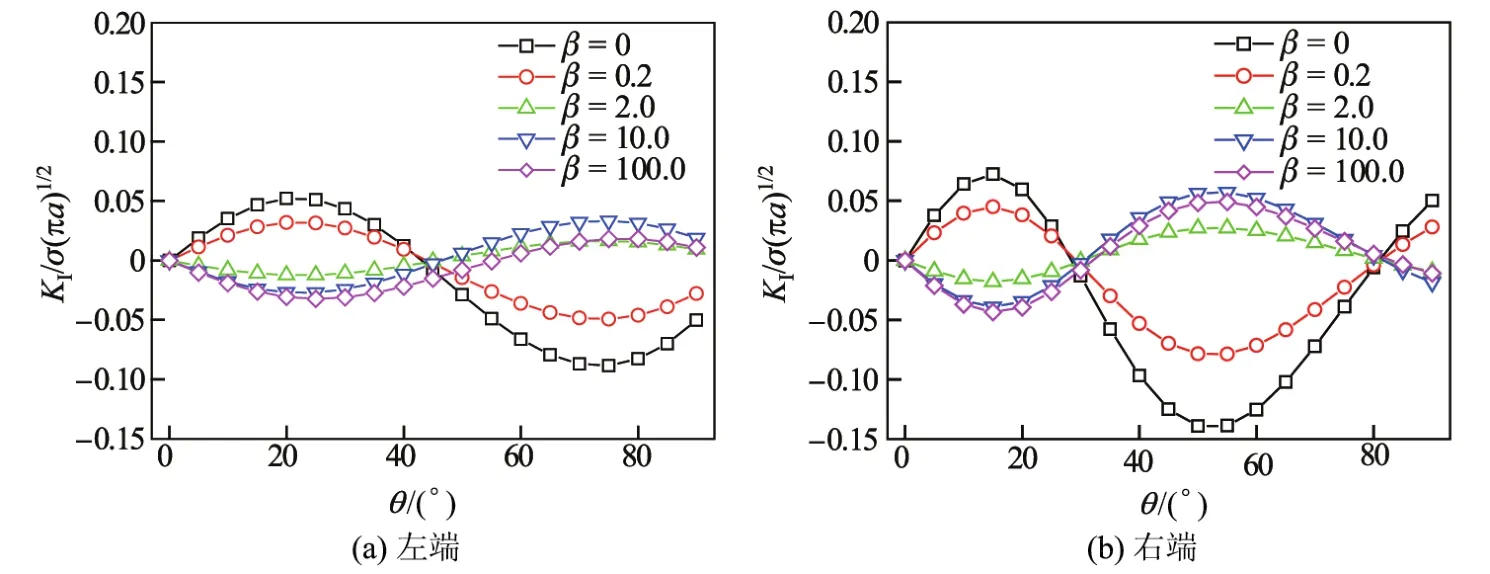
图7　裂纹左端和右端Ⅱ型应力强度因子与粒子方位角的关系(水平裂纹)Fig.7　TypeⅡSIF at left tip and right tip of crack as a function of particle bearing angle (horizontal crack)

图6为裂纹保持水平位置不变时,左端和右端Ⅰ型应力强度因子与粒子方位角的关系.图7为Ⅱ型应力强度因子与粒子方位角的关系.由图6和7可知,由于裂纹右端与粒子的距离较近,Ⅰ型和Ⅱ型应力强度因子的变化幅度都比裂纹左端的变化幅度要大.值得注意的是,软粒子与硬粒子对应力强度因子变化幅度的影响恰恰相反.

图8为裂纹方向同步变化时裂纹左端和右端Ⅰ型应力强度因子与粒子方位角的关系.由图可知,无论在裂纹的左端还是右端,Ⅰ型应力强度因子随粒子方位角均呈单调变化,但裂纹右端的Ⅰ型应力强度因子对模量比的变化比左端更加敏感.图9为裂纹左端和右端Ⅱ型应力强度因子与粒子方位角的关系.由图可知,无论在裂纹的左端还是右端,Ⅱ型应力强度因子随粒子方位角均呈先增后减的变化,裂纹右端的Ⅱ型应力强度因子对模量比的变化同样比左端更加敏感.

图8　裂纹左端和右端Ⅰ型应力强度因子与粒子方位角的关系(倾斜裂纹)Fig.8　TypeⅠSIF at left tip and right tip of crack as a function of particle bearing angle (inclined crack)

图9　裂纹左端和右端Ⅱ型应力强度因子与粒子方位角的关系(倾斜裂纹)Fig.9　TypeⅡSIF at left tip and right tip of crack as a function of particle bearing angle (inclined crack)

2.3裂纹与粒子的长宽比

图10为裂纹和粒子的长宽比.对裂纹面和粒子界面分别采用NG=15和N=40个节点进行离散,计算粒子长宽比对附近裂纹的应力强度因子的影响,结果如图11所示.由图11可知,当粒子长宽比变化时,裂纹左端和右端应力强度因子的变化趋势是相同的,只是右端应力强度因子变化的幅度较大.在图10所示构型的情况下,具有较小长宽比的软粒子使得应力强度因子增大,而具有较大长宽比的硬粒子使得应力强度因子减小.

图11　裂纹左端和右端Ⅰ型应力强度因子与粒子长宽比的关系Fig.11　TypeⅠSIF at left tip and right tip of crack as a function of particle aspect ratio

图12　裂纹与粒子的水平距离Fig.12　Horizontal distance between crack and particle

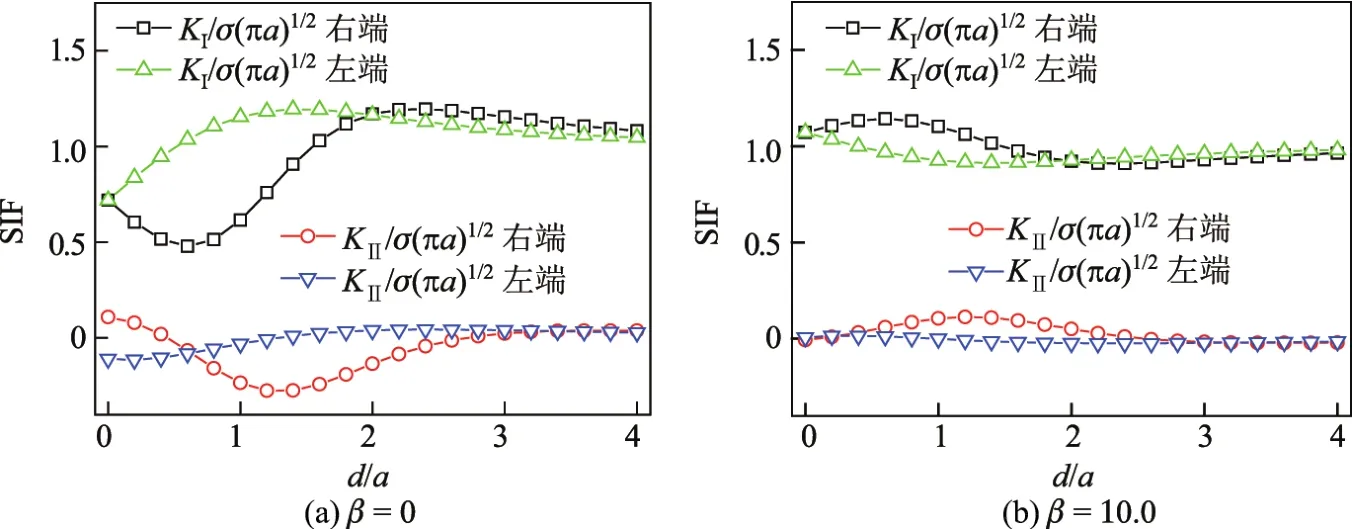
图13　裂纹应力强度因子与圆形孔洞或圆形粒子水平距离的关系Fig.13　SIF as a function of horizontal distance of circular hole or particle

2.4裂纹与粒子(或孔洞)的水平距离

裂纹与粒子(或孔洞)水平排列,如图12所示.对裂纹面和粒子界面分别采用NG= 15和N=40个节点进行离散,考察裂纹与粒子(或孔洞)的水平距离对应力强度因子的影响,计算结果如图13和14所示.由图13可知,圆形孔洞对应力强度因子的影响比圆形粒子要大,特别是当水平距离较小时.图14的结果与图13相似,方形孔洞对应力强度因子的影响比方形粒子要大.比较图13和14的结果可知,同样条件下方形孔洞对应力强度因子的影响比圆形孔洞要大,因为方形孔洞对周围基体应力场的干扰更大.

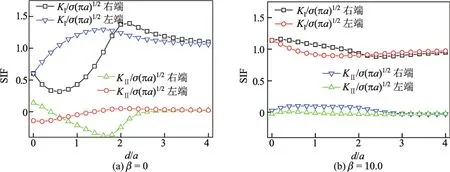
图14　裂纹应力强度因子与方形孔洞或方形粒子水平距离的关系Fig.14　SIF as a function of horizontal distance of square hole or particle

3　结束语

针对含有缺陷的非均质弹性固体,即同时含有粒子(或孔洞)和裂纹的情况,建立了全空间中粒子和裂纹位移间断形式的对偶边界积分方程计算模型,解决了全空间条件下难以对所研究对象进行直接加载的问题.采用边界积分方程的离散形式对含有少量粒子和裂纹的典型情况进行了数值分析,其中对粒子边界(或界面)采用边界点法进行离散,对裂纹面采用高斯配点法进行离散.采用裂纹整体信息,即通过与裂纹张开位移对应的裂纹虚拟面力来计算应力强度因子,可以获得稳定和精确的计算结果.

对含有少量粒子和裂纹的典型情况进行了数值分析,计算了裂纹的应力强度因子,通过与已有研究结果的比较,对计算模型与计算机程序的正确性与可靠性进行了验证,并探讨了粒子与裂纹的相互作用.

[1]ALIABADI M H,ROOKE D P.Numerical fracture mechanics[M].Southampton：Computational Mechanics Publications,1991：140-192.

[2]CRUSET A.Boundary element analysis in computational fracture mechanics[M].Dordrecht：Kluwer Academic Publishers,1988：17-60.

[3]黎在良,王元汉,李廷芥.断裂力学中的边界数值方法[M].北京：地震出版社,1996：237-265.

[4]YAN X Q.Stress intensity factors for cracks emanating from a triangular or square hole in an infinite plateby boundary elements[J].Engineering Failure Analysis,2005,12(3)：362-375.

[5]YAN X Q.A brief evaluation of approximation methods for microcrack shielding problems[J]. ASME Journal of Applied Mechanics,2006,73(4)：694-696.

[6]MA H,GUO Z G,DHANASEKAR M,et al.Efficient solution of multiple cracks in great number using eigen COD boundary integral equations with iteration procedure[J].Engineering Analysis with Boundary Elements,2013,37(3)：487-500.

[7]GUO Z,LIU Y,MA H,et al.A fast multipole boundary element method for modeling 2-D multiple crack problems with constant elements[J].Engineering Analysis with Boundary Elements,2014, 47(1)：1-9.

[8]DONG C Y,CHEUNG Y K,LO S H.An integral equation approach to the inclusion-crack interactions in three-dimensional infinite elastic domain[J].Computational Mechanics,2002,29(4/5)：313-321.

[9]DONG C Y,LO S H,CHEUNG Y K.Numerical analysis of the inclusion-crack interactions using an integral equation[J].Computational Mechanics,2003,30(2)：119-130.

[10]DONG C Y,LEEK Y.A new integral equation formulation of two-dimensional inclusion-crack problems[J].International Journal of Solids and Structures,2005,42(18/19)：5010-5020.

[11]DONG C Y,LEE K Y.Boundary element analysis of infinite anisotropic elastic medium containing inclusions and cracks[J].Engineering Analysis with Boundary Elements,2005,29(6)：562-569.

[12]DONG C Y.The integral equation formulations of an infinite elastic medium containing inclusions,cracks and rigid lines[J].Engineering Fracture Mechanics,2008,75(13)：3952-3965.

[13]DONG C Y,YANG X,PAN E.Analysis of cracked transversely isotropic and inhomogeneous solids by a special BIE formulation[J].Engineering Analysis with Boundary Elements,2011, 35(2)：200-206.

[14]CHEN Y Z.Boundary integral equation method for two dissimilar elastic inclusions in an infinite plate[J].Engineering Analysis with Boundary Elements,2012,36(1)：137-146.

[15]MA H,ZHOU J,QIN Q H.Boundary point method for linear elasticity using constant and quadratic moving elements[J].Advances in Engineering Software,2010,41(3)：480-488.

[16]TELLES J C F,CASTOR G S,GUIMARAES S.A numerical Green’s function approach for boundary elements applied to fracture mechanics[J].International Journal for Numerical Methods in Engineering,1995,38(19)：3259-3274.

[17]HUI C Y,SHIA D.Evaluations of hypersingular integrals using Gaussian quadrature[J].International Journal for Numerical Methods in Engineering,1999,44(2)：205-214.

[18]MURAKAMI Y,KEER L M.Stress intensity factors handbook[J].Journal of Applied Mechanics, 1993,60(4)：1063.

本文彩色版可登陆本刊网站查询：http://www.journal.shu.edu.cn

Dual boundary integral equations and numerical solutions for particles and cracks in full space

MA Hang1,PAN Meng2
(1.College of Sciences,Shanghai University,Shanghai 200444,China；
2.Shanghai Institute of Applied Mathematics and Mechanics,Shanghai University, Shanghai 200072,China)

As elastic solids contain particles and cracks,a computational model is proposed for the analysis of particles and cracks in full space using dual boundary integral equations in the displacement discontinuity formulation.The method avoids the difficulty of loading the objects under study in full space.Numerical analysis is carried out for some typical cases with a few particles and cracks using a discrete form of boundary integral equations.A boundary point method and Gauss collocation are used for discretization of the particle boundary or interface,and the crack surface,respectively.The stress intensity factors of cracks are computed.Mutual effects between particles and cracks are investigated and compared with those in the literature,verifying correctness and reliability of the proposed computational model and the program.

particle；crack；dual boundary integral equation；numerical solution；stress intensity factor

O 241

A

1007-2861(2016)05-0533-12

10.3969/j.issn.1007-2861.2015.02.020

2015-05-11

国家自然科学基金资助项目(11272195,11332005)

马杭(1951—),男,教授,博士生导师,博士,研究方向为计算固体力学. E-mail:hangma@staff.shu.edu.cn