线性加荷情况下非饱和土层一维固结特性分析

秦爱芳,葛航

(上海大学土木工程系,上海　200072)

线性加荷情况下非饱和土层一维固结特性分析

秦爱芳,葛航

(上海大学土木工程系,上海200072)

基于Fredlund非饱和土一维固结理论,得到了线弹性和黏弹性两种地基在线性加荷情况下,顶面透水透气、底面不透水不透气的单层非饱和土一维固结超孔隙水压力、超孔隙气压力和沉降的半解析解.通过典型算例,分析了不同水、气渗透系数比以及不同土层深度下超孔隙水压力、超孔隙气压力和固结度随时间的变化规律，并对线弹性和黏弹性两种地基的计算结果进行了比较分析.得到的结论对于非饱和土固结特性的研究及线性加荷下的固结工程具有一定的参考价值.

非饱和土；半解析解；一维固结；线荷载

地球表面非饱和土的覆盖率较高,非饱和土的固结问题在实际工程中也较为常见.地基处理工程中常采用预压固结,即线性加荷到一定值后稳定使其固结.线性加荷情况下非饱和土的固结特性研究对于地基预压等工程问题很有意义.

Therzaghi[1]和Biot[2]的饱和土固结理论虽然比较成熟,但并不适用于非饱和土.非饱和土中由于有气体的存在,其固结特性要比饱和土复杂得多.

自20世纪60年代,人们就开始对非饱和土固结进行研究,但由于非饱和土的复杂性,至今没有统一的固结理论.国外比较经典的有Fredlund等[3]、Barden[4]提出的固结方程，国内Chen等[5-6]、杨代泉等[7]也提出了各自的非饱和土固结方程.目前非饱和土固结理论中具有代表性和权威性的是Fredlund的非饱和土固结理论及方程.

秦爱芳等[8-10]在Fredlund非饱和土一维固结理论的基础上进行假设,得到了大面积均布瞬时加载单面排水条件下的非饱和土线弹性地基一维固结的解析解、加荷随时间指数变化下线弹性地基一维固结的解析解和大面积均布瞬时加载下黏弹性地基一维固结的半解析解.实际工程中更多的是线性加荷情况.对于线性加荷情况下的饱和土,谢康和等[11-12]研究了变荷载下饱和土的一维大应变固结解析理论，李传勋等[13-15]进行了变荷载下基于指数渗流的单层、双层线弹性地基一维固结分析.

本工作基于Fredlund非饱和土的一维固结理论,得到线性加荷情况下顶面为透水透气面、底面为不透水和不透气面的非饱和土层一维固结的半解析解,并且针对线弹性和黏弹性两种情况进行比较分析.研究结果对地基预压等线性加荷下地基固结问题具有参考价值.

1　基本理论

1.1基本假定

本研究基本假定如下：①土粒和水分界面在外力作用下保持平衡；②气相是连续的；③土体的体积变化系数在固结中保持不变；④液相、气相渗透系数均为基质吸力的函数,在固结过程中非线性变化,在足够小的时间段内假定为常数；⑤不考虑土中水与空气的相互溶解及扩散；⑥土颗粒与水均不可压缩,固结过程中非饱和土体的总体积变化等于液相和气相体积变化之和；⑦固结过程中所有应变均为小应变.

1.2线弹性

计算模型如图1所示,取单层非饱和土,土层厚为H,顶面为排水排气面,底面为不排水不排气面,线性加荷为

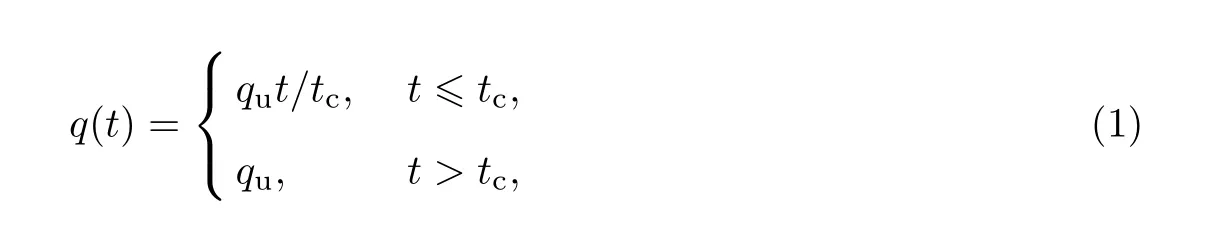
式中，qu=100 kPa,tc=105s.荷载随时间的变化规律如图2所示.

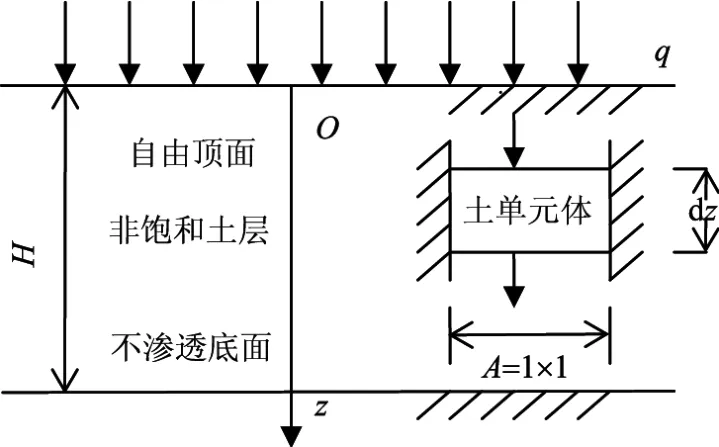
图1　计算模型Fig.1　Calculation model

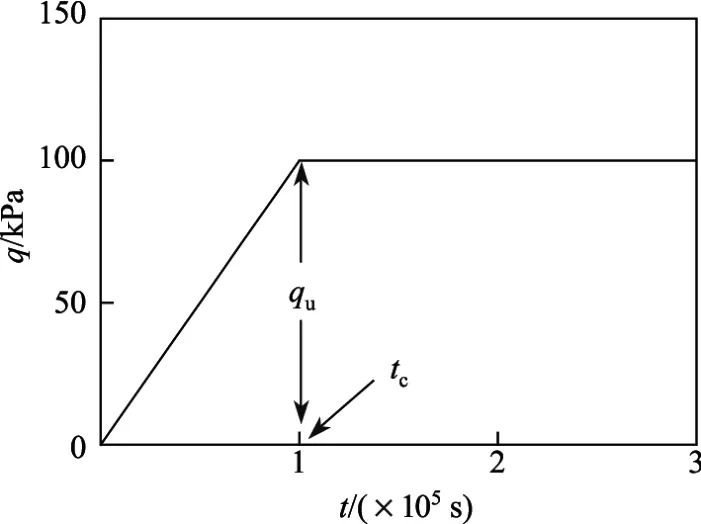
图2　荷载随时间的变化Fig.2　Load variation over time

1.2.1液相控制方程

基于Fredlund非饱和土的一维固结理论,可以得到线性加荷情况下的液相控制方程,方法同文献[9],

其中ua,uw为超孔隙气压力和超孔隙水压力,kw为水渗透系数,γw为水的重度,mw1k为K0加荷下相应于净法向应力变化d(σ−ua)的水体积变化系数,mw2为K0加荷条件下相应于基质吸力变化d(ua−uw)的水体积变化系数.

1.2.2气相控制方程

基于Fredlund非饱和土的一维固结理论,也可以得到线性加荷情况下的气相控制方程,方法同文献[9],

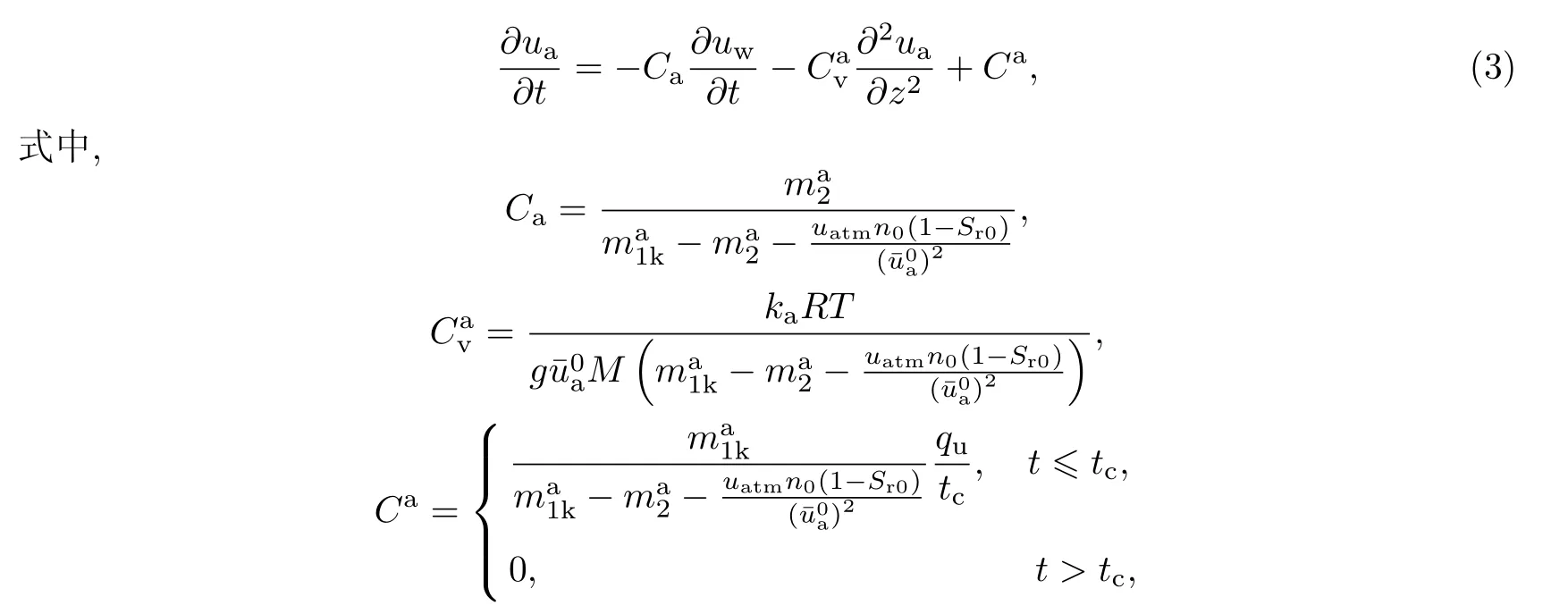
其中ka为气渗透系数,M为平均摩尔质量,R=8.314 J/(mol·K)为通用气体常数,T为绝对温度,g为重力加速度,n0为加载前的初始孔隙率,Sr0为加载前的初始饱和度,为初始绝对孔隙气压力,uatm为大气压,为K0加荷下相应于净法向应力变化d(σ−ua)的气体积变化系数,为K0加荷条件下相应于基质吸力变化d(ua−uw)的气体积变化系数.

1.2.3矩阵微分方程

达西定律：

式中,hw为水头,且hw=z+uw/γw.

空气传导系数修正后的气体流动Fick定律：

将式(2)～(5)分别进行Laplace变换,得到如下矩阵形式的偏微分方程,方法同文献[9],

其中s为Laplace变量.

1.2.4Laplace变换下求解

利用Cayley-Hamilton理论求解矩阵微分方程(6),可以得到顶面状态向量与任意深度处状态向量间的关系：

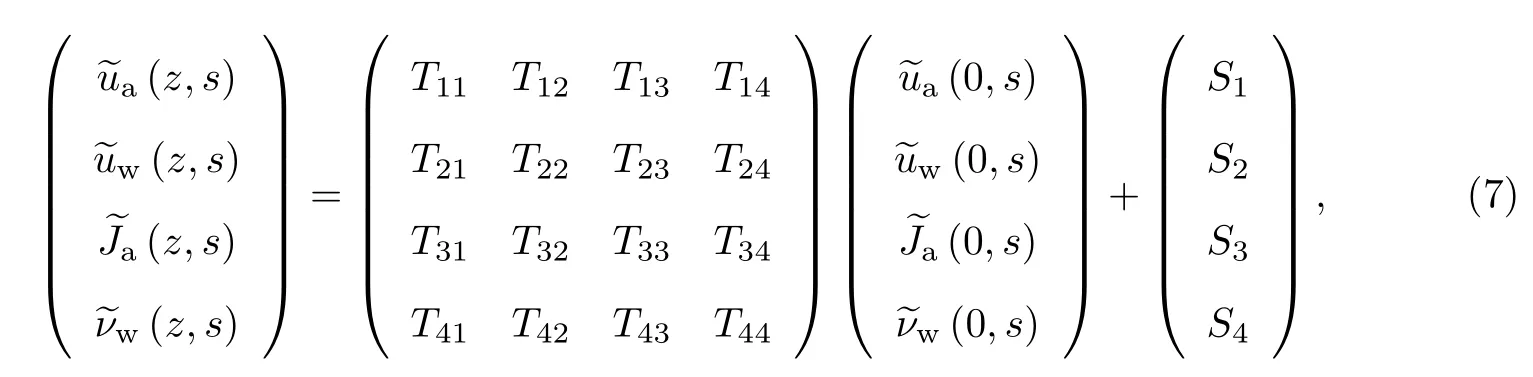
式中,Tij以及S1～S4的求解方法同文献[9],其中

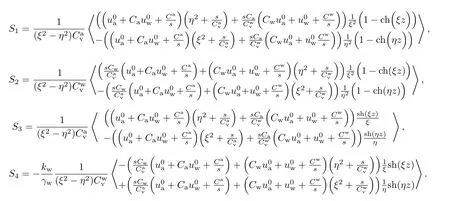
边界条件(顶面透水透气、底面不透水不透气)：

初始条件：

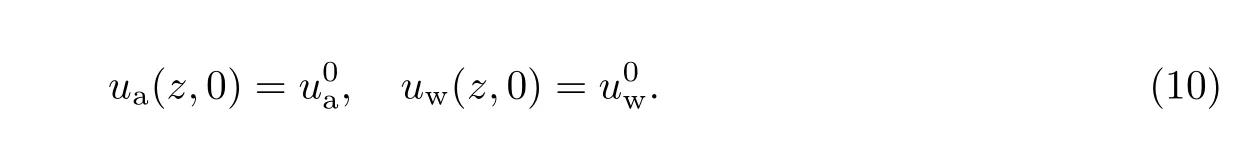
最终可以得到Laplace变换下任意深度超孔隙水压力和超孔隙气压力的表达式,方法同文献[9],

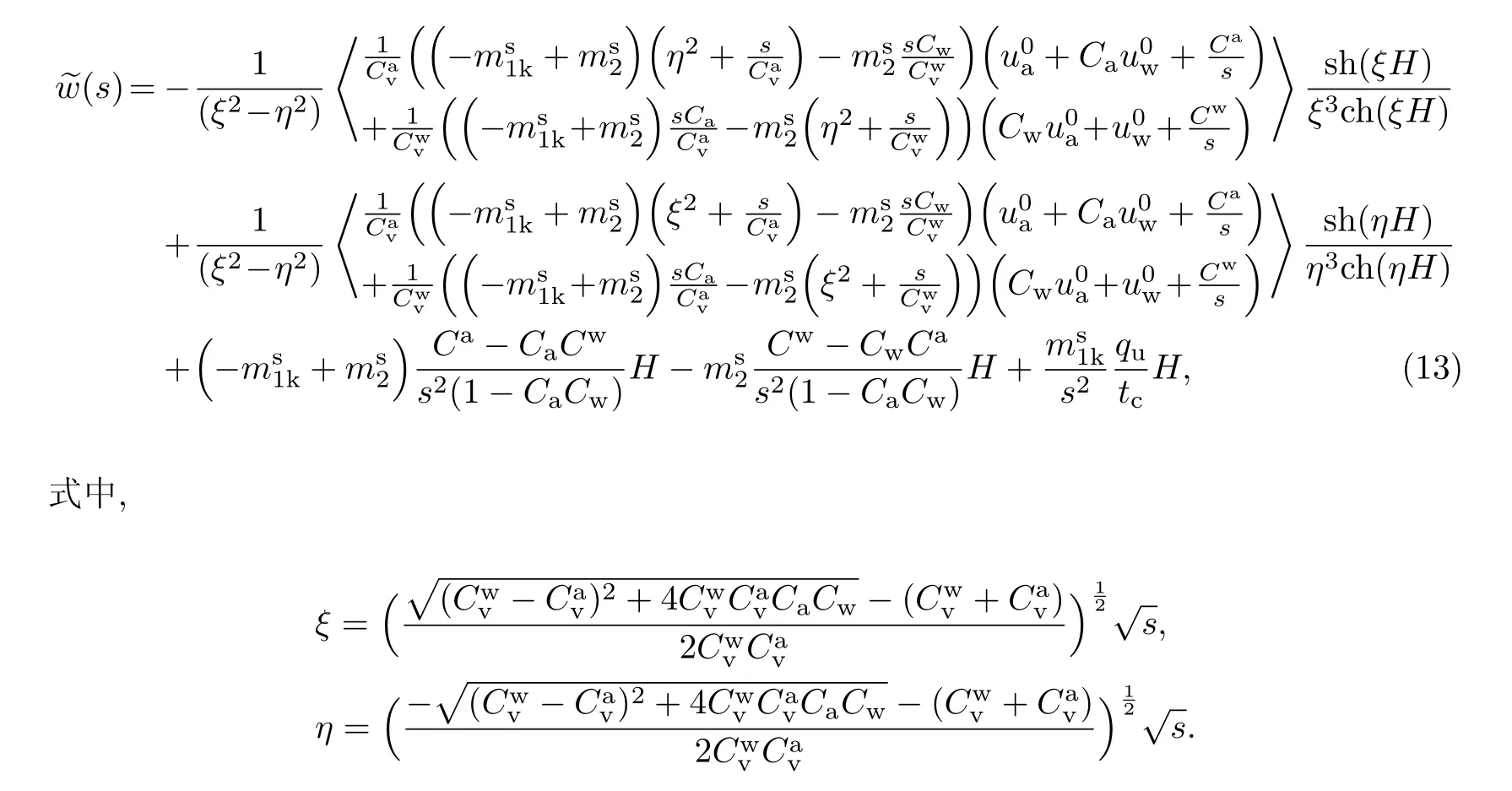
1.3黏弹性

黏弹性情况采用Merchant本构模型,如图3所示.该模型由一个弹性体和Kelvin体串联而成.本构方程为

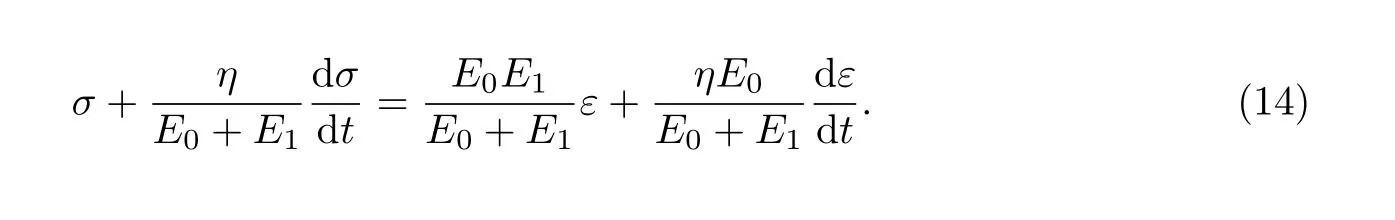
图3　Merchant模型Fig.3　Merchant model

对式(13)作关于时间t的Laplace变换,可得

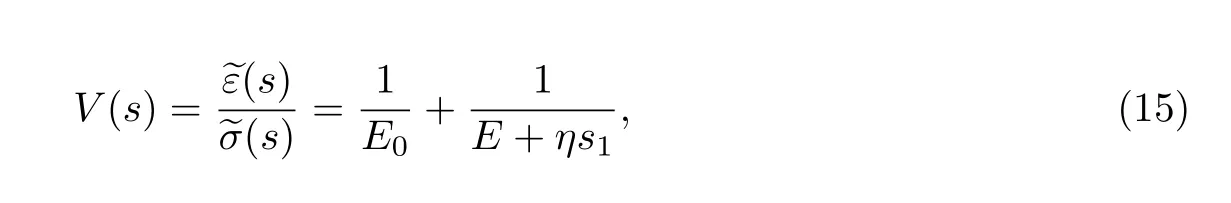
式中,V(s)为柔度系数的Laplace变换式.

采用李氏比拟法,引入柔度系数的Laplace变换式V(s)来代替线弹性模型中的常数1/E,直接对连续方程和本构方程进行Laplace变换,得到控制方程,进而求得黏弹性情况下Laplace变换域内的解,方法同文献[10],

采用Crump[16]给出的方法编制程序,对式(11)～(13)及式(16)～(18)进行Laplace逆变换,即得到线弹性及黏弹性有限厚度土层一维固结超孔隙水压力、超孔隙气压力以及土层沉降的半解析解.

2　算例与分析

2.1算例

对固结过程中的超孔隙水压力、超孔隙气压力以及固结度随时间的变化规律进行分析,结果如图4～8所示,其中固结度是整个固结过程中土层某一时刻的固结量与最终沉降量的比值.

2.2分析

(1)图4为线弹性和黏弹性线性加荷情况下ka/kw不同时ua/qu的变化.可以看出：随着荷载的增加,超孔隙气压力增大,当加荷稳定时达到最高值,然后开始消散；ka/kw越大,消散的时间越短.整个消散阶段曲线陡降较大,说明消散是在短时间内完成的.黏弹性和线弹性的整体趋势是相似的,但由于黏滞系数的存在,使得超孔隙气压力的增长受阻,因此黏弹性情况下超孔隙气压力的峰值较线弹性要小.

(2)图5为线弹性和黏弹性线性加荷情况下ka/kw不同时uw/qu的变化.可以看出：随着荷载的增加,超孔隙水压力增大,当加荷稳定时达到最高值,然后开始消散；消散曲线中有一段平台期,ka/kw越大,到达平台期的时间越短；在超孔隙水压力消散结束后,无论ka/kw大小如何,超孔隙水压力消散曲线都趋于一致.与超孔隙气压力情况类似,黏弹性和线弹性的整体趋势是相似的,但由于黏滞系数的存在,使得超孔隙水压力的增长受阻,因此黏弹性情况下超孔隙水压力的峰值较线弹性要小.

图4　z=8m时不同ka/kw情况下ua/qu随时间的变化规律Fig.4　Changes in ua/quwith time under different ka/kwwhen z=8 m

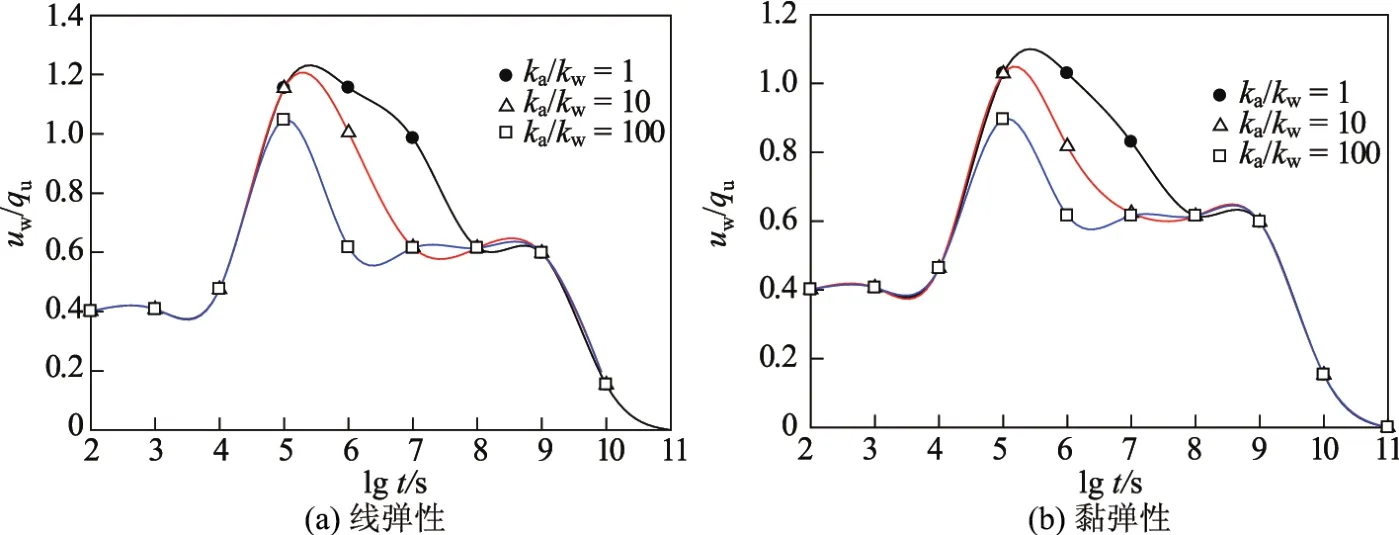
图5　z=8 m时不同ka/kw情况下uw/qu随时间的变化规律Fig.5　Changes in uw/quwith time under different ka/kwwhen z=8 m

(3)图6为线弹性和黏弹性线性加荷情况下ka/kw不同时固结度的变化.对应于超孔隙水压力的变化,固结度变化曲线也有一个平台期.平台期之前为超孔隙气压力和超孔隙水压力快速消散的阶段,固结速度较快；ka/kw越大,到达平台期的时间越短；在超孔隙气压力消散结束后,无论ka/kw大小如何,固结度变化曲线都趋于一致；黏弹性和线弹性的整体趋势是相似的,但由于黏滞系数的存在,使得黏弹性固结的过程较为平缓,平台期亦不明显.

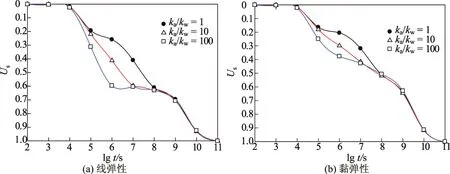
图6　z=8 m时不同ka/kw情况下固结度随时间的变化规律Fig.6　Changes in degree of consolidation with time under different ka/kwwhen z=8 m

(4)图7为线弹性和黏弹性线性加荷情况下土层深度不同时ua/qu的变化.由图可知,深度越深,超孔隙气压力消散至同一水平的时间就越长.这是因为深度越深,离排气面就越远,渗透路径越长.黏弹性与线弹性情况相似.

图7　ka/kw=10时不同z/H情况下ua/qu随时间的变化规律Fig.7　Changes in ua/quwith time under different z/H when ka/kw=10

(5)图8为线弹性和黏弹性线性加荷情况下土层深度不同时uw/qu的变化.由图可知,土层深度越深,超孔隙水压力消散至同一水平的时间就越长；当超孔隙水压力消散完成时,超孔隙水压力出现了一段平缓的曲线段,且深度越深,平缓段越长.黏弹性与线弹性情况相似.

图8　ka/kw=10时不同z/H情况下uw/qu随时间的变化规律Fig.8　Changes in uw/quwith time under different z/H when ka/kw=10

2.3验证

将上述针对非饱和土算例的分析结果退化到饱和土的情况,并与饱和土情况下的解进行比较验证.

2.3.1Laplace变换下饱和土的解

Gibson等[17]给出的加荷随时间变化的饱和土单向固结的微分方程为

令σ=q(t)(t≤tc),可得到线荷载作用下饱和土的固结微分方程：

结合式(4),用类似于非饱和土的推导方法,对式(4)和(20)分别进行Laplace变换,组成矩阵形式的偏微分方程：

利用Cayley-Hamilton理论求解此矩阵微分方程,可以得到顶面状态向量与任意深度处状态向量间的关系,通过引入边界条件求得边界向量,最后可以得到Laplace变换下任意深度超孔隙水压力的表达式：

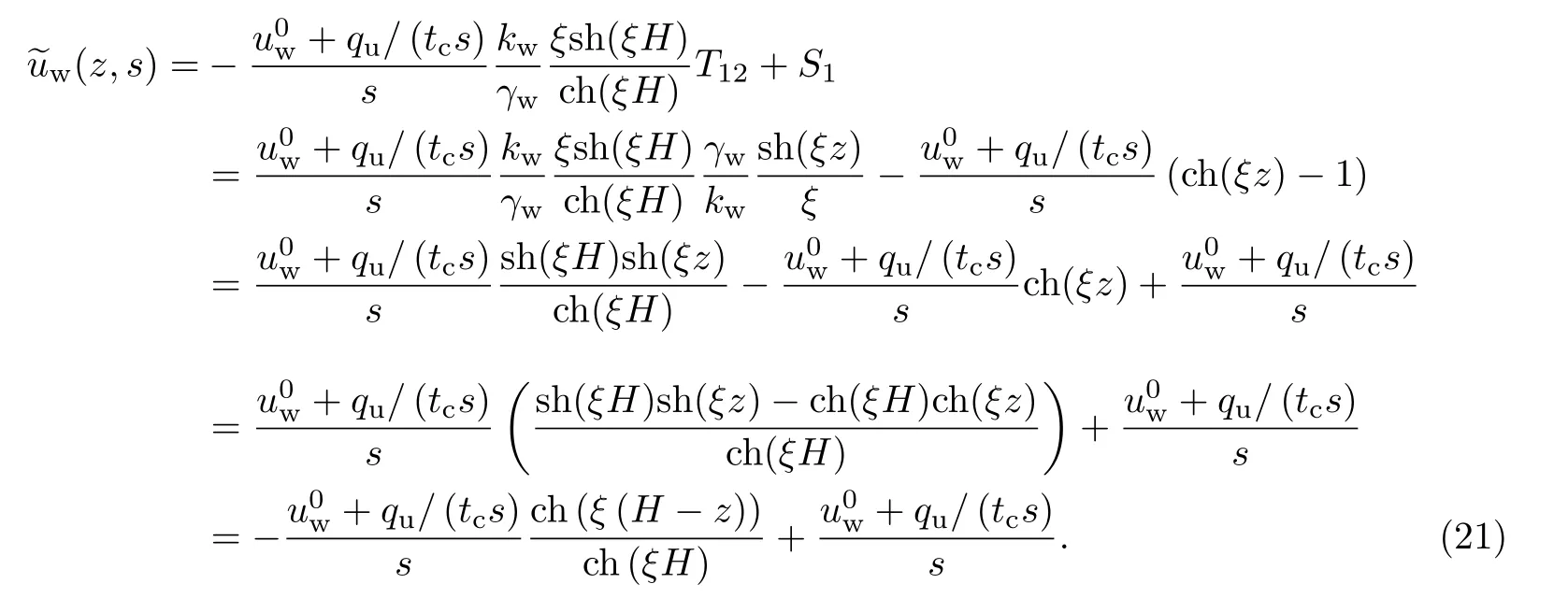
2.3.2非饱和土退化为饱和土的解对于饱和土,式(11)中,

将上述参数代入式(12),可得

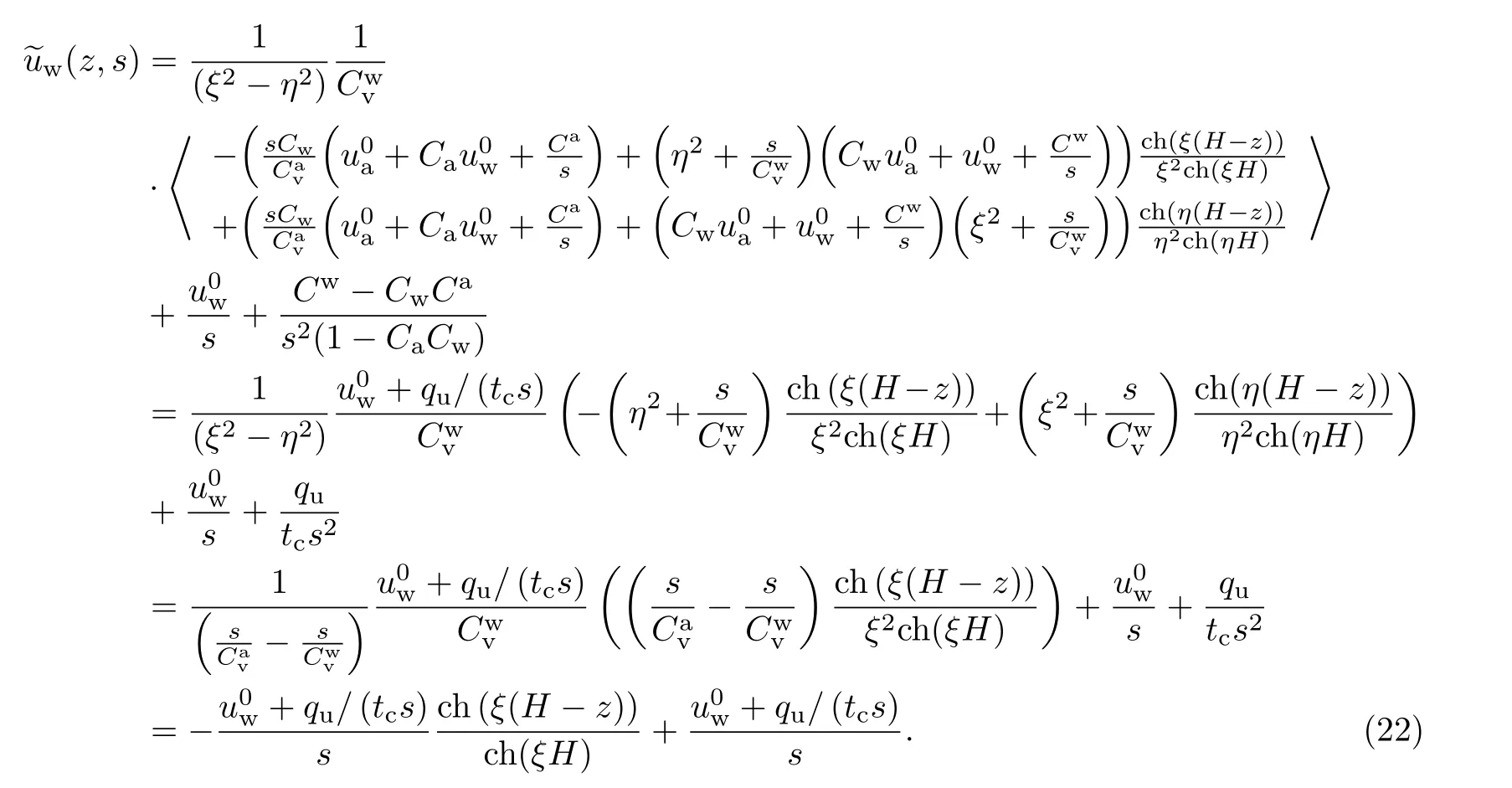
由式(22)可以看出,退化后的解与饱和土的解一致.

3　结论

本工作在求得线弹性和黏弹性地基的单层非饱和土一维固结超孔隙水压力、超孔隙气压力和沉降的半解析解的基础上,分析了不同工况下超孔隙水压力、超孔隙气压力和固结度的变化规律.研究结果表明：

(1)在线荷载作用下线弹性和黏弹性情况超孔隙气压力、超孔隙水压力的消散规律相似.但由于土的黏性使得黏弹性情况下的峰值较线弹性情况要小,固结相对平缓.

(2)超孔隙气压力要先于超孔隙水压力消散完成,消散时间较短,其中ka/kw越大,超孔隙气压力消散越快.超孔隙水压力在超孔隙气压力消散完成以后会有一个平台期,ka/kw越大,抵达平台期的时间越短,且平台期越长；但过了平台期以后,无论ka/kw如何变化,消散曲线都一致.

(3)离透水透气面越远,渗透路径越长,超孔隙气压力和超孔隙水压力消散至同一水平的时间就越长,且超孔隙水压力的平台期越长.

[1]THERzAGHI K.Erdbaumechanik auf bodenphysikalischen Grundlagen[M].Wien：Deuticke, 1925.

[2]BIOT M A.General theory of three-dimensional consolidation[J].Journal of Applied Physics, 1941,12(2)：155-164.

[3]FREDLUND D G,HASAN J U.One-dimensional consolidation theory：unsaturated soils[J].Canadian Geotechnical Journal,1979,16(3)：521-531.

[4]BARDEN L.Consolidation of compacted and unsaturated clays[J].Geotechnique,1965,15(3)：267-286.

[5]CHEN Z H,XIE D Y,LIU Z D.Consolidation theory of unsaturated soil based on the theory of mixture(Ⅰ)[J].Applied Mathematics and Mechanics(English Edition),1993,14(2)：137-150.

[6]CHEN Z H.Consolidation theory of unsaturated soil based on the theory of mixture(Ⅱ)[J]. Applied Mathematics and Mechanics(English Edition),1993,14(8)：687-698.

[7]杨代泉,沈珠江.非饱和土一维固结简化计算[J].岩土工程学报,1991,13(5)：70-78.

[8]QIN A F,CHEN G J,TAN Y W,et al.Analytical solution to one-dimensional consolidation in unsaturated soils[J].Applied Mathematics and Mechanics(English Edition),2008,29(10)：1329-1340.

[9]QIN A F,SUN D A,TAN Y W.Semi-analytical solution to one-dimensional consolidation in unsaturated soils[J].Applied Mathematics and Mechanics(English Edition),2010,31(2)：215-226.

[10]秦爱芳,罗坤,孙德安.非饱和土粘弹性地基一维固结特性分析[J].上海大学学报(自然科学版), 2010,16(2)：203-209.

[11]谢康和,潘秋元.变荷载下任意层地基一维固结理论[J].岩土工程学报,1995,17(5)：80-85.

[12]谢康和,郑辉,LEO C J.变荷载下饱和软黏土一维大应变固结解析理论[J].水利学报,2003,34(10)：6-13.

[13]李传勋,胡安峰,谢康和,等.变荷载下考虑非达西渗流的一维固结半解析解[J].岩石力学与工程学报,2011,30(S2)：3937-3943.

[14]李传勋,谢康和,卢萌盟,等.变荷载下基于指数形式渗流的一维固结分析[J].岩土力学,2011, 32(2)：553-559.

[15]李传勋,谢康和,卢萌盟,等.变荷载下基于指数渗流双层地基一维固结分析[J].岩土力学,2012, 33(5)：1565-1571.

[16]CRUMp K S.Numerical inversion of Laplace transforms using a Fourier series approximation[J]. Journal of the ACM,1976,23(1)：89-96.

[17]GIBSON R E,ScHIFFMAN R L,CARGILL K W.The theory of one-dimensional consolidation of saturated clays.Ⅱ.Finite nonlinear consolidation of thick homogeneous layers[J].Canadian Geotechnical Journal,1981,18(2)：280-293.

本文彩色版可登陆本刊网站查询：http://www.journal.shu.edu.cn

Analysis of one-dimensional consolidation characteristics in unsaturated soil under line loads

QIN Aifang,GE Hang
(Department of Civil Engineer,Shanghai University,Shanghai 200072,China)

Semi-analytical solutions of excess pore-air pressure,excess pore-water pressure and degree of consolidation are obtained based on the Fredlund’s one-dimensional consolidation theory for unsaturated soil.The research object is a layer of unsaturated soil whose top surface is penetrable,and the bottom surface impenetrable to water and air.With a typical example,rules of excess pore-air pressure,excess pore-water pressure and degree of consolidation changing with time in different soil depth and ratio of permeability coefficient of air and water are analyzed.The linear elastic and viscoelastic situations are calculated, analyzed and compared.The conclusions are useful in the research of unsaturated soil consolidation characteristics and practical engineering problems about consolidation under line loads.

unsaturated soil；semi-analytical solution；one-dimensional consolidation；line load

TU 44

A

1007-2861(2016)05-0624-13

10.3969/j.issn.1007-2861.2015.01.002

2015-01-17

上海市自然科学基金资助项目(13ZR1416200)；上海市教委科研创新基金资助项目(13YZ018)

秦爱芳(1966—),女,教授,博士生导师,博士,研究方向为岩土力学与工程. E-mail:qinaifang@shu.edu.cn