突加集中荷载作用下饱和土-深埋圆形隧道衬砌系统的非轴对称动力响应

陆剑骏,杨骁

(上海大学土木工程系,上海　200072)

突加集中荷载作用下饱和土-深埋圆形隧道衬砌系统的非轴对称动力响应

陆剑骏,杨骁

(上海大学土木工程系,上海200072)

考虑饱和土与深埋圆形衬砌的相互作用,研究了突加集中荷载作用下饱和土-衬砌系统的非轴对称动力响应.基于Biot理论和弹性理论,采用Laplace变换和Fourier级数,考虑衬砌边界条件以及衬砌与饱和土交界面处的连续性条件,在Laplace变换域内求得突加集中荷载作用下饱和土-弹性衬砌耦合系统的位移、应力和孔隙水压力等的解析表达式.利用Laplace逆变换Crump数值反演方法得到饱和土-衬砌系统动力响应的数值解,并分析了土体和衬砌系统的力学、几何等参数对系统动力响应的影响.结果表明：5倍隧道衬砌半径以外处土体的动力响应远小于隧道附近土体的动力响应；衬砌刚度和厚度对土体位移和应力影响显著,但对孔隙水压力影响较小；孔隙水的可压缩性对土体位移的幅值影响不大,但对应力幅值的影响较为显著.

饱和土；弹性衬砌；集中荷载；动力响应；Laplace变换

随着城市建设的发展,土地资源日益紧张,地下空间的开发利用显得尤为重要.地下隧道是地下工程的常见结构形式之一,常用于交通、人防和管线.隧道在全寿命运营周期内可能受到动荷载的作用,如机车突加荷载和振动、碰撞以及爆炸等.瞬间的动力作用会对隧道结构和周围土体产生较大影响,因此研究地下隧道在突加荷载作用下的瞬态响应不仅具有重要的理论意义,也能够为隧道安全性的评估提供指导.

近年来,基于饱和土的Biot理论[1-2]和多孔介质理论[3-4],饱和土中隧道的动力特性和动力响应已有较丰富的研究成果.除深埋隧道动力特性的研究成果[5-10]外,Senjuntichai等[11]研究了不同荷载下饱和弹性介质中圆形隧道的动力响应,杨峻等[12]利用积分变换法给出了饱和土体中圆柱形孔洞动力响应解.将衬砌等效为弹性Flügge壳体,Zakout等[13]研究了弹性土体中圆形隧道动力响应；丁伯阳等[14]基于Green函数给出了饱和土中矩形隧道承受集中荷载的振动位移；刘干斌等[15]研究了饱和黏弹性土体中隧道开挖的土体应力和位移变化.考虑隧道衬砌的影响,Lu等[16]将衬砌视为片状弹性体,采用微分求积法数值研究了饱和弹性土中隧道的动力响应；Gao等[17]解析研究了不同荷载作用下弹性衬砌深埋圆形隧道饱和弹性土的动力响应.将衬砌等效为Flügge壳体,蔡袁强等[18]研究了简化爆炸荷载作用下圆形隧道饱和土的动力响应.这些工作揭示了饱和土和衬砌系统的动力学行为.然而,上述研究成果主要针对深埋圆形隧道饱和土-衬砌系统的轴对称动力响应,而关于饱和土-深埋隧道衬砌系统的非轴对称动力响应研究成果则较少[19],其中非轴对称变形的动力特性,如振动沿环向的传播规律等有待深入研究.

基于饱和土的Biot模型,本工作研究了饱和弹性土-深埋圆形隧道衬砌耦合系统在突加集中荷载作用下的非轴对称动力响应.首先,将问题视为平面应变问题,基于饱和土的Biot理论,通过引入势函数,利用分离变量法和Laplace变换,得到饱和土在Laplace变换域中的动力响应通解；其次,将隧道衬砌变形分别视为平面应变问题和Flügge壳体,得到衬砌的动力响应通解.在此基础上,利用隧道衬砌和饱和土接触面处的连续性条件及边界条件,得到Laplace变换域中饱和土-衬砌耦合系统非轴对称的位移、应力和孔隙水压力解析解,并利用Laplace逆变换的Crump方法,得到时间域中饱和土-衬砌系统的瞬态位移、应力和孔隙水压力响应.在验证本工作理论和算法的基础上,数值研究了饱和弹性土-深埋圆形隧道衬砌耦合系统在突加集中荷载作用下的动力响应,分析了不同隧道模型和材料参数等对饱和土动力响应的影响.

1　问题描述及饱和土控制方程求解

图1为饱和土中深埋圆形隧道的示意图.设无限饱和弹性土体中有衬砌厚度为h的无限长圆形隧道承受径向集中压力f(θ,t)=p(t)δ(θ)的作用,其中δ(θ)为delta函数.衬砌的内外半径分别为R1和R2,平均半径R=(R1+R2)/2,h=R2−R1.假设饱和土-衬砌系统的动力响应为小变形,且土体与弹性衬砌完全接触,二者间无相对滑移,接触面处不渗透.根据圆形隧道几何和荷载分布特征,可以将饱和土-衬砌系统的动力响应视为非轴对称平面应变问题.

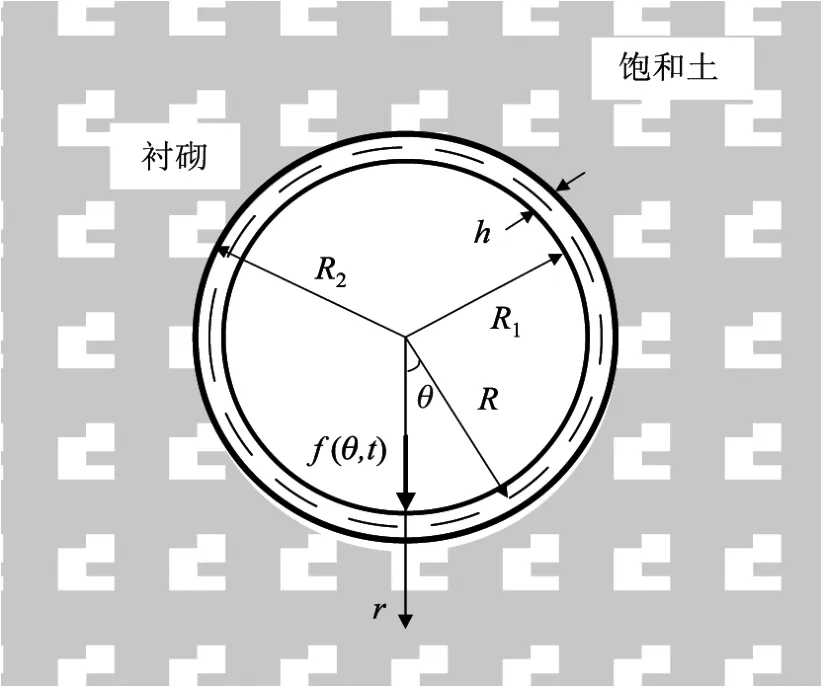
图1　饱和土中的深埋圆形隧道Fig.1　Circular tunnel deeply embedded in saturated soil

记饱和土平面应变的径向和环向位移分别为uSr和uSθ,且uS=(uSr,uSθ,0),而孔隙水相对于土体骨架的径向和环向位移分别为wr和wθ,且w=(wr,wθ,0),则根据饱和土的Biot理论[1-2],饱和弹性土的动力方程为

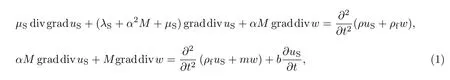
式中,λS和µS为饱和土体的表观Lame常数；α和M分别为反映土骨架和孔隙流体压缩性的常数；ρf为孔隙水的真实密度,饱和土体的表观密度为ρ=(1−n)ρS+nρf,其中n为孔隙率, ρS为土骨架的真实密度；m=ρf/n；b=η0/kd为流固相互作用系数,其中η0和kd分别为流体的黏滞系数和动力渗透系数.

应力-应变本构关系可以表示为

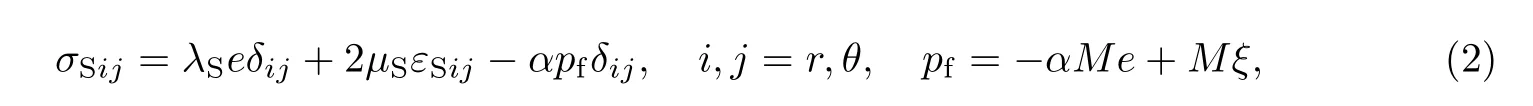
式中,σSij(i,j=r,θ)为土体的总应力；δij为Kronecker符号；e和ξ分别为土体和孔隙流体的体积应变,e=divuS,ξ=−divw；εSij(i,j=r,θ)为土骨架的应变；pf为孔隙水压力.

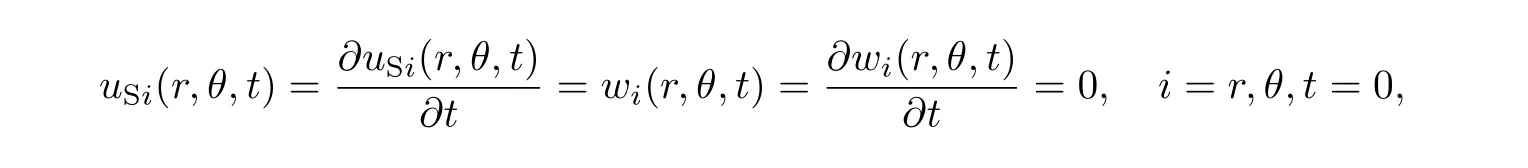
并引入如下无量纲参数：

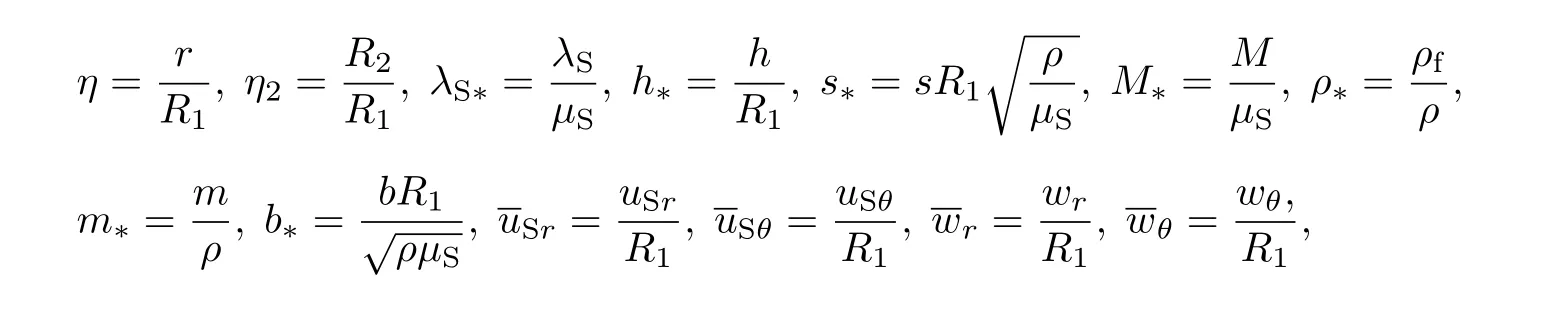
可得极坐标中Laplace变换域内饱和弹性土的无量纲控制方程为

引入如下位移势函数：

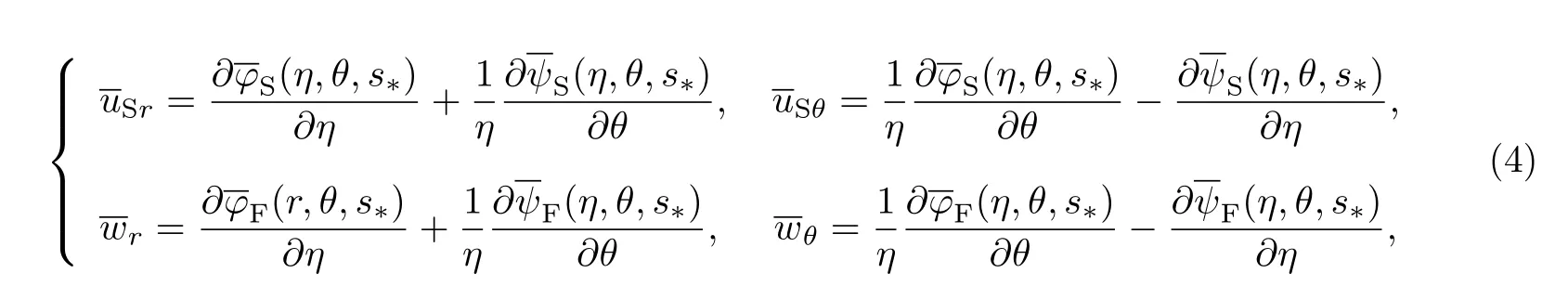
则方程(3)可化为

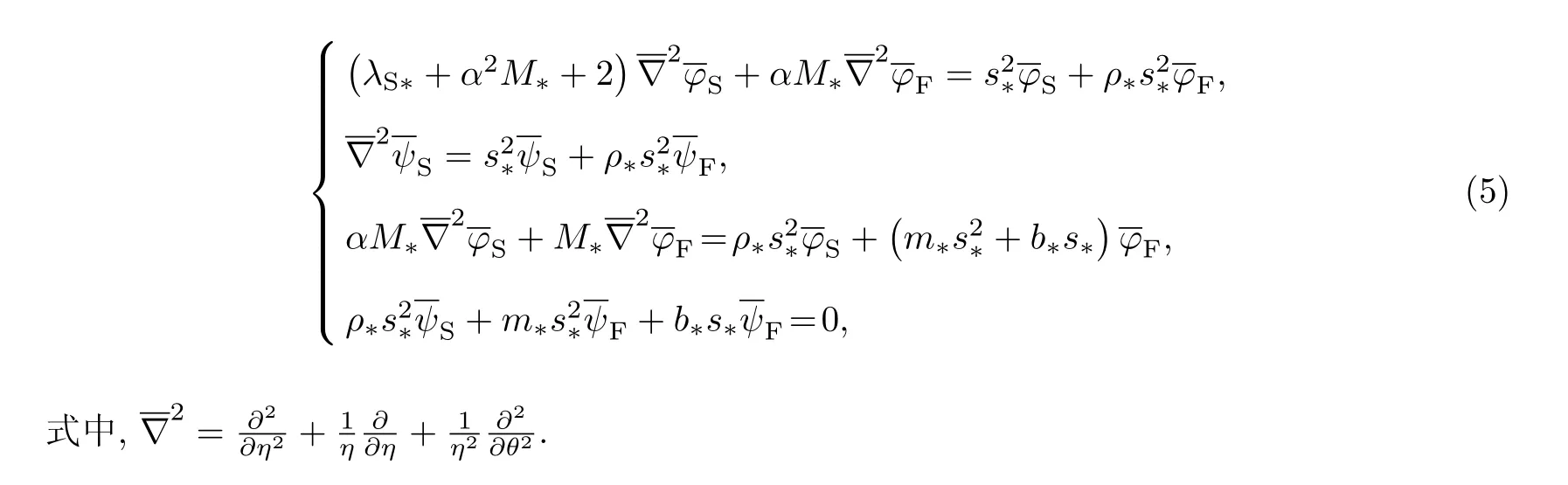
方程(5)可进一步解耦为

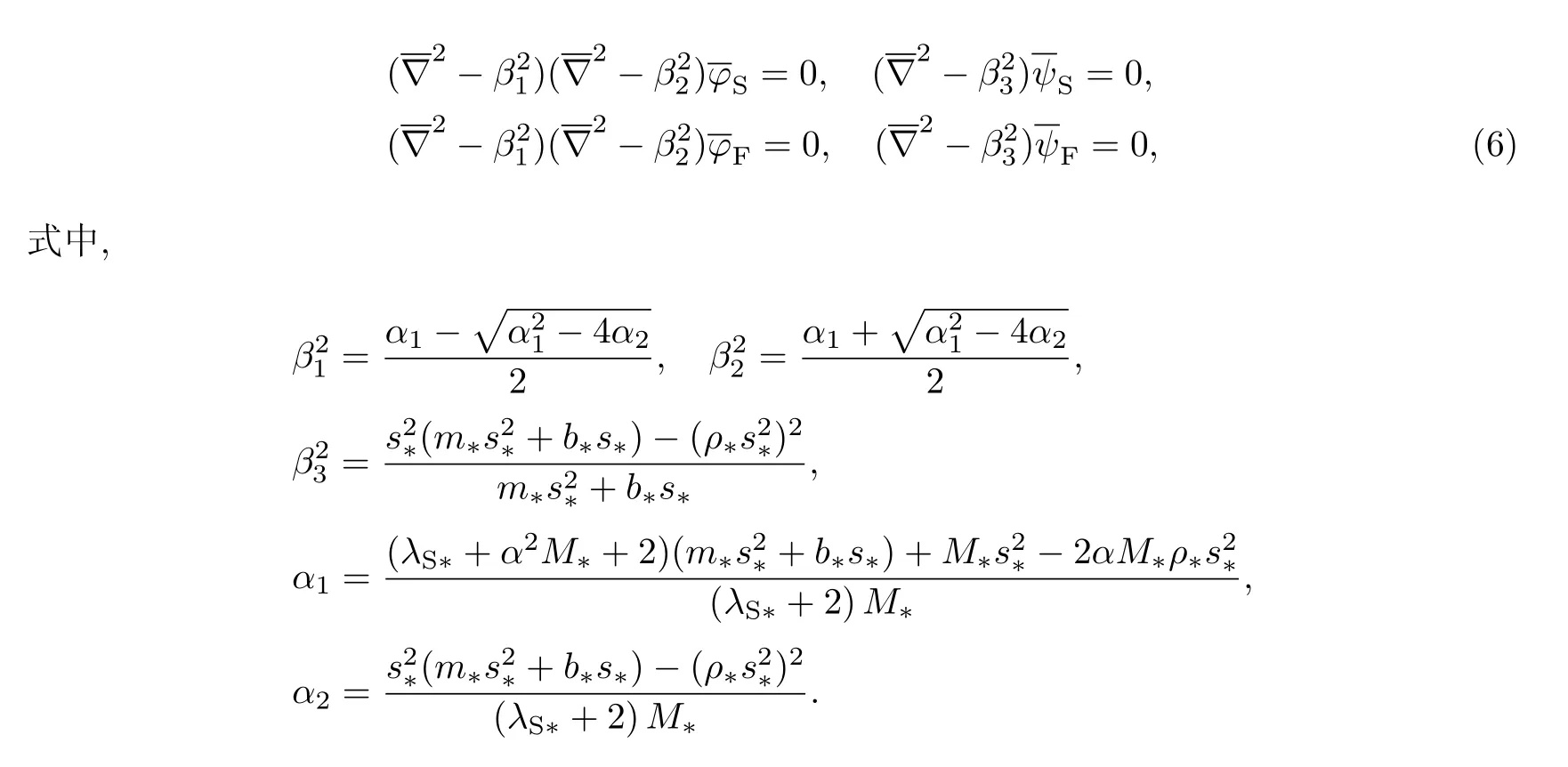
由于隧道承受的径向集中压力f(θ,t)在极轴上,因此可设位移势函数为

式中,Kn(·)为n阶第二类变形Bessel函数；Bn,Dn,En为待定常数；

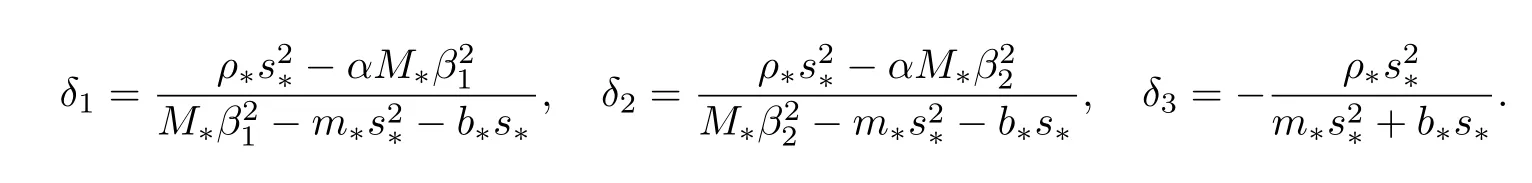
利用方程(2)和(4)可求得Laplace变换域中饱和土的位移和应力以及孔隙水的相对位移和压力：

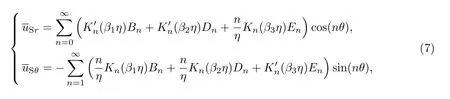
2　衬砌的控制方程及求解

2.1平面应变模型

将弹性衬砌视为平面应变问题,设衬砌的径向和环向位移分别为uLr和uLθ,且uL= (uLr,uLθ,0),则衬砌的动力方程为

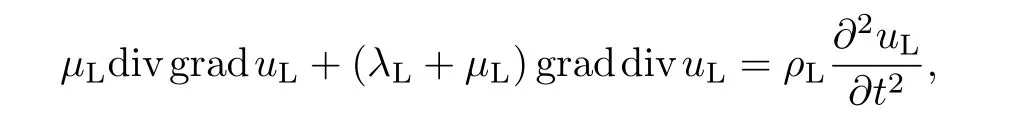
式中,λL和µL为衬砌的Lame常数,ρL为衬砌密度.

衬砌的应力-应变本构关系为

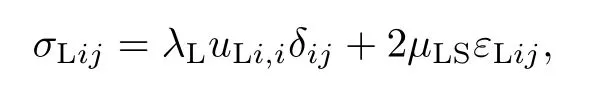
式中,σLij(i,j=r,θ),εLij(i,j=r,θ)分别为衬砌的应力和应变.

考虑初始条件

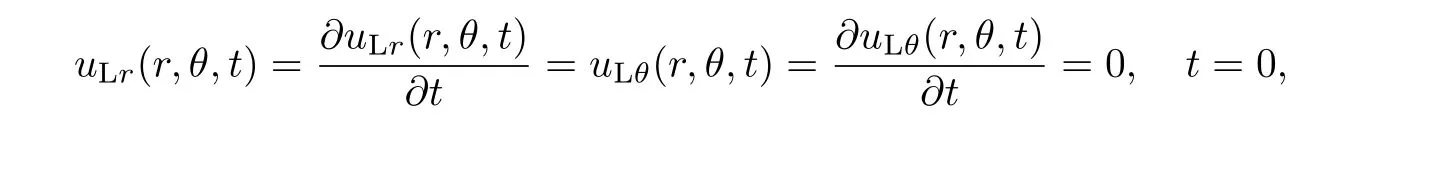
利用Laplace变换,并引入如下无量纲参数：

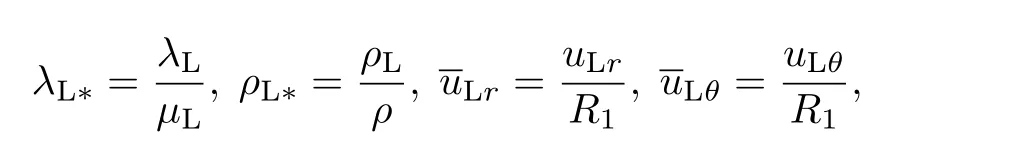
可得衬砌在Laplace变换域中的无量纲控制方程为

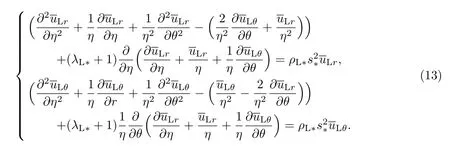
类似地,引入衬砌位移势函数

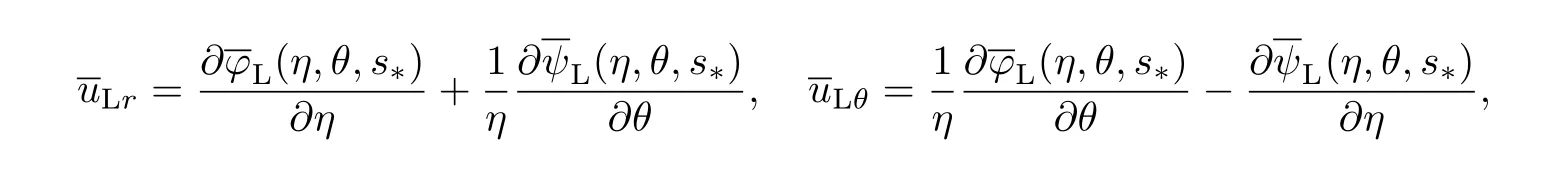
由方程(13)可得

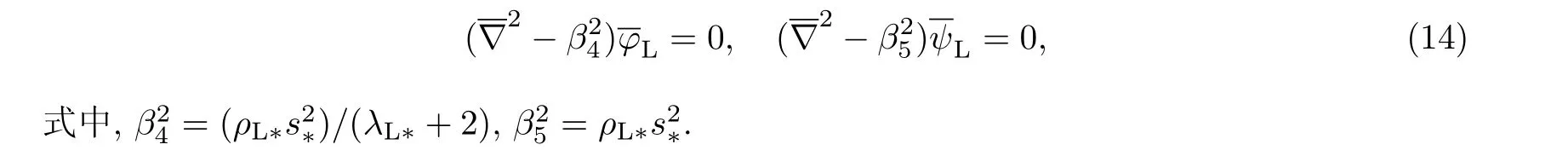
假设弹性衬砌的位移势函数为

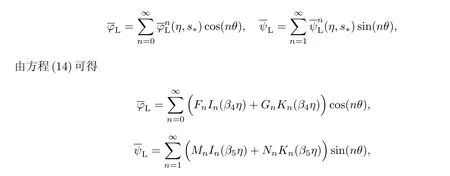
式中,In(·)为n阶第一类变形Bessel函数；Fn,Gn,Mn,Nn为待定常数.

因此,由衬砌的应力-应变关系以及位移势函数可求得弹性衬砌在Laplace变换域内的位移和应力分别为

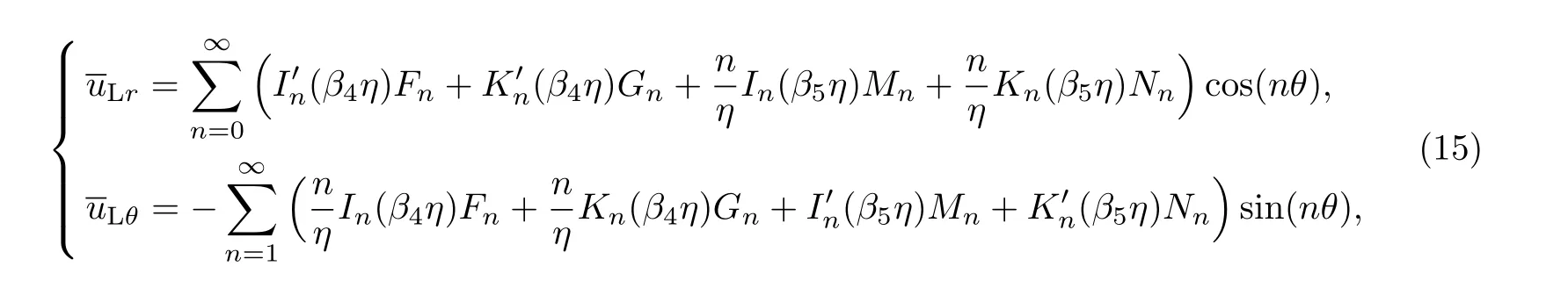
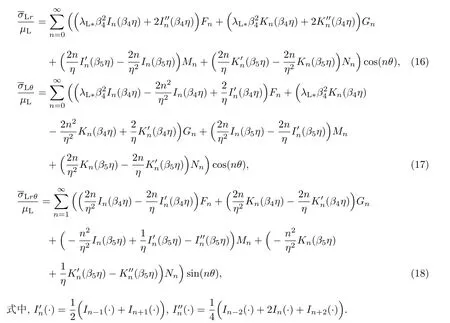
2.2Flügge壳体模型

若将衬砌等效为薄壁圆柱壳体,在无扭矩条件下,根据Flügge壳体理论[13],衬砌的运动方程可表示为

并对方程(19)进行Laplace变换,可得

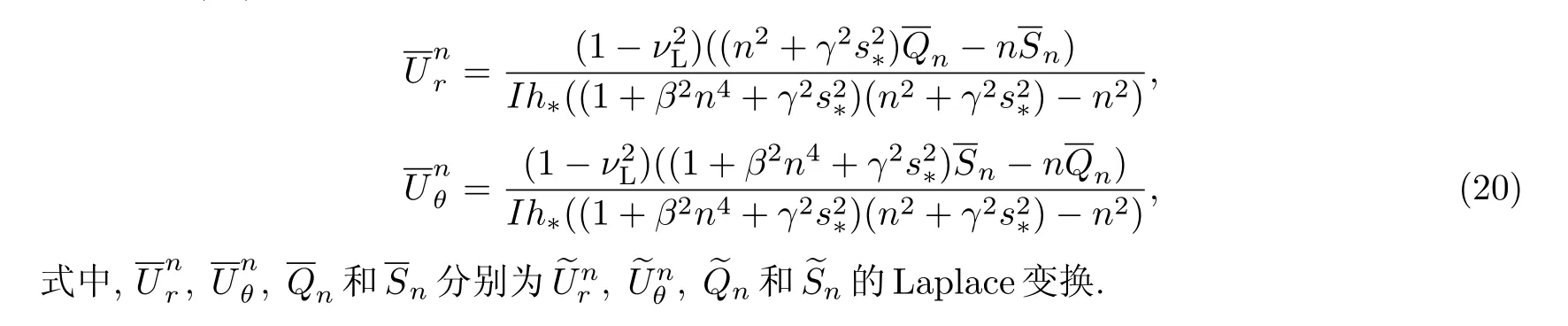
3　边界条件

隧道内部承受的径向突加集中常荷载p(t)=p0H(t)关于θ的Fourier展式及其Laplace变换分别为

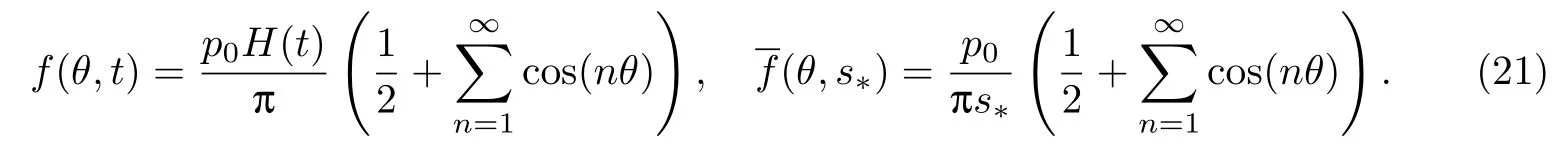
3.1饱和土-平面应变模型衬砌系统

设饱和土与弹性衬砌完全接触,则衬砌与土体交界面处的位移和应力均连续.由于地下隧道通常需保持干燥无水的运营环境,因此不考虑衬砌的透水性,即衬砌与土体接触面处不渗透,由此可得Laplace变换域中土体和衬砌接触面(η=η2)处的连续性条件为

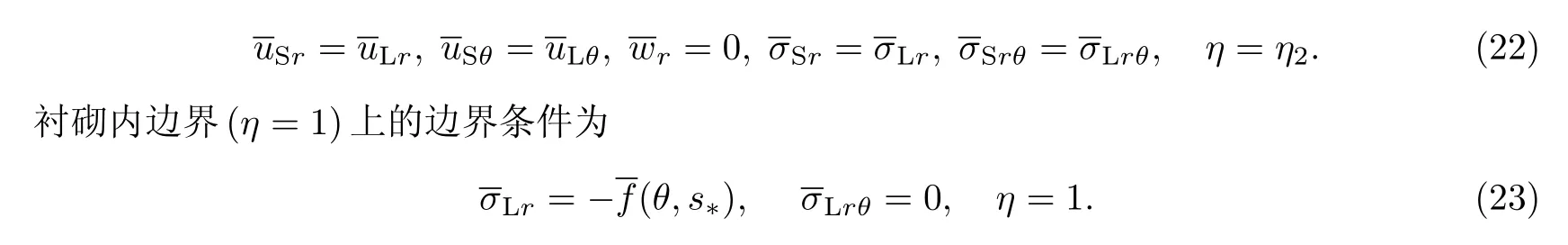
由式(7)～(11),(15)～(18)和(21)～(23)可得,待定常数Bn,Dn,En,Fn,Gn,Mn,Nn(n=0, 1,…)满足线性方程组

3.2饱和土-Flügge壳体模型衬砌系统

若将衬砌结构视为圆柱壳体,当衬砌厚度h远小于隧道中曲面半径R时,可以将衬砌的中曲面(r=R)视为衬砌和土体的接触面,即忽略h/2[13].在饱和土与弹性衬砌完全接触且接触面处不渗透的条件下,Laplace变换域中衬砌与土体接触面(η=ηm=(1+η2)/2)上的连续性条件和应力协调条件为

3.3无衬砌隧道

若不考虑隧道衬砌的影响,即隧道无衬砌,有R1=R2,则Laplace变换域中饱和土动力响应的边界条件为

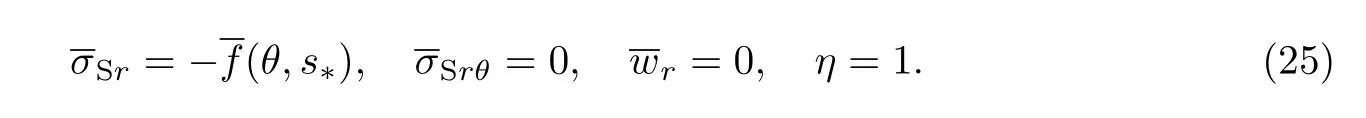
类似地,可得到确定待定常数Bn,Dn和En的线性代数方程组,从而确定待定常数Bn,Dn和En.

为求得饱和土-衬砌系统在时间域中的动力响应,需对Laplace变换域中的解进行Laplace逆变换,然而通常情况下很难求得相应解Laplace逆变换的解析表达式.因此,本工作采用Laplace逆变换的Crump数值算法[20],得到饱和土-衬砌耦合系统在时间域中的动力响应结果.

4　数值结果和分析

4.1对比验证

为了验证本工作中模型和Crump数值逆变换计算结果的正确性和可靠性,对均布突加荷载作用下无衬砌隧道的轴对称动力响应[11]进行对比分析.令n=0,h∗=0,ρL∗=1, λS∗=λL∗和µS∗=µL∗,并按文献[11]取

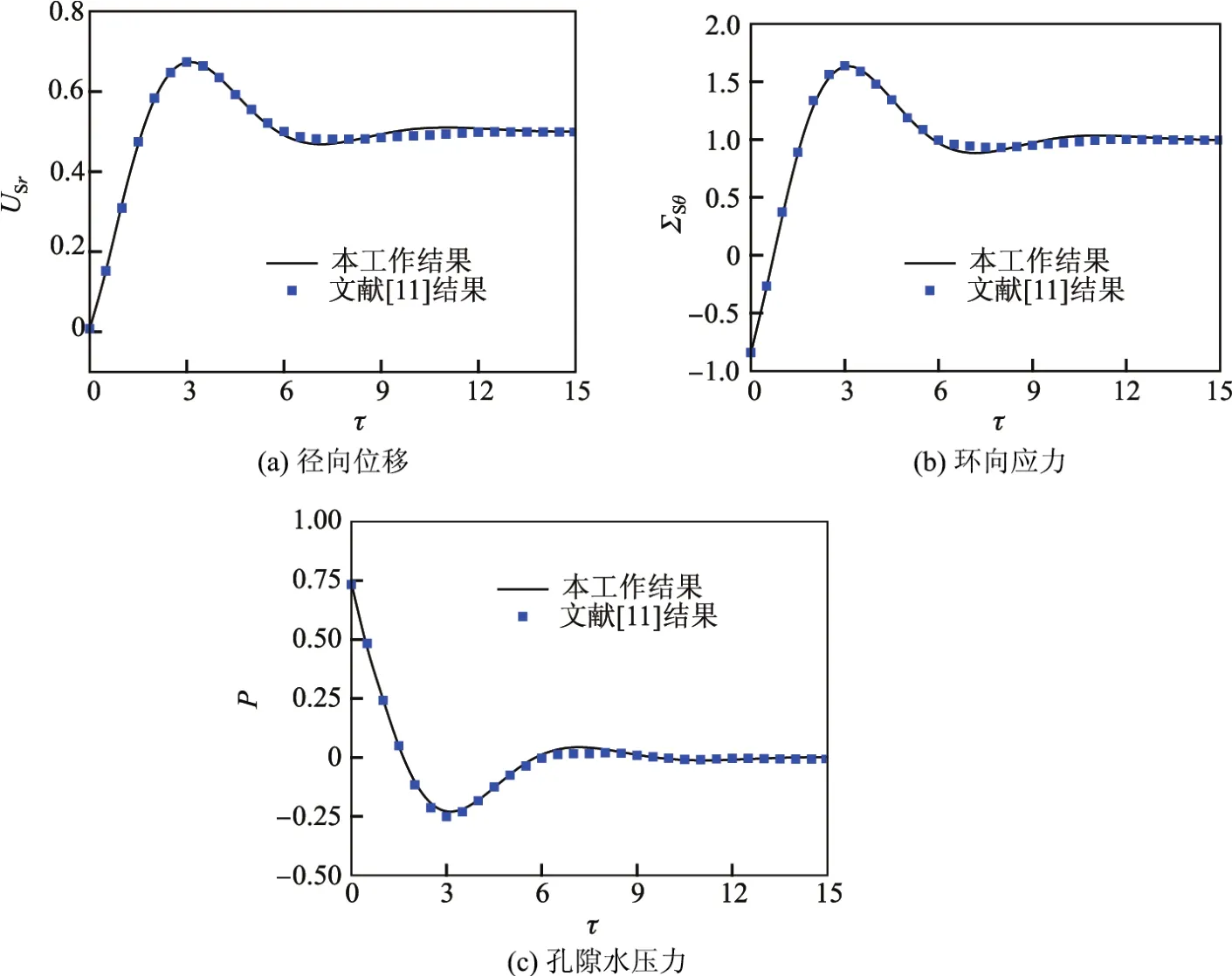
图2　本工作数值结果与文献[11]结果的比较Fig.2　Result comparisons between numerical results presented in this paper and those in Ref.[11]

图2给出了无衬砌隧道边界(η=1)处土体无量纲径向位移USr、无量纲环向应力ΣSθ和无量纲孔隙水压力P在均布突加荷载作用下随无量纲时间τ的响应.由图可见,当τ＜5时,采用本工作中的方法得到的数值结果与文献[11]中的结果吻合良好；当τ＞5时,二者略微有所区别,原因是本工作采用的Laplace数值逆变换方法与文献[11]中的方法有所不同,且Crump反演方法的结果具有更明显的波动性质,计算结果更加准确[21].

4.2参数分析

在通常情况下,可采用3种模型研究隧道附近饱和土的力学性能,即无衬砌饱和土隧道模型、将衬砌视为二维平面问题的饱和土-衬砌耦合系统模型和将衬砌视作无扭矩薄壁圆柱壳体的饱和土-壳体衬砌耦合系统模型.

采用表1给出的参数,分析饱和土-隧道衬砌系统在突加集中荷载作用下的动力响应.由于采用Fourier级数进行分析,因此所得数值结果依赖于Fourier级数的项数选取.通过数值计算发现,当选取Fourier级数项数n≥15时,响应增加的幅值小于10-3,故本工作取n=15进行相关的数值计算.

表1　计算参数Table 1　Parameters for calculation

图3给出了3种隧道模型中θ=0°处USr,P以及θ=90°处ΣSθ随τ的动力响应.可见,饱和土-衬砌耦合系统模型与无衬砌饱和土隧道模型的径向位移、环向应力和孔隙水压力随时间的响应性态基本一致,而饱和土-壳体衬砌耦合系统模型的响应小于饱和土-平面应变衬砌耦合系统模型的响应,并且径向位移响应差值较大,衬砌可明显降低土体的径向位移和环向应力,但对孔隙水影响很小.另外,当τ≈3时,径向位移和环向应力达到峰值,孔隙水压力最小；而在突加荷载作用的瞬间,孔隙水压力最大.而后,随着时间的延长,由于孔隙水和土体颗粒相互作用的阻尼性质,土体位移和应力逐渐趋为常数,孔隙水压力逐渐消散,土骨架承担荷载.

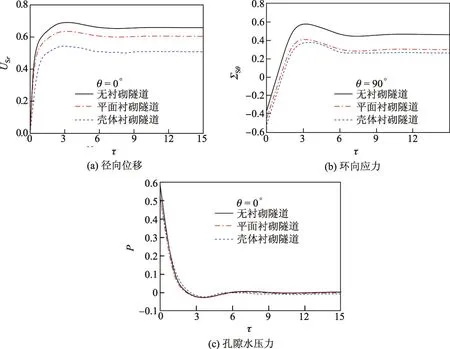
图3　集中突加常荷载作用下饱和土的动力响应Fig.3　Dynamic responses of saturated soil under the constant step load

图4给出了饱和土-平面应变衬砌耦合系统在τ值不同时土体的USr,ΣSθ和P沿η= r/R1的分布.可见,土体响应具有振动性质.当τ较小时,较远位置η处的响应为0,表明突加集中荷载引起的响应尚未传播至该处,并且离隧道较远(η≥5)处的土体动力响应远小于隧道附近土体的动力响应.

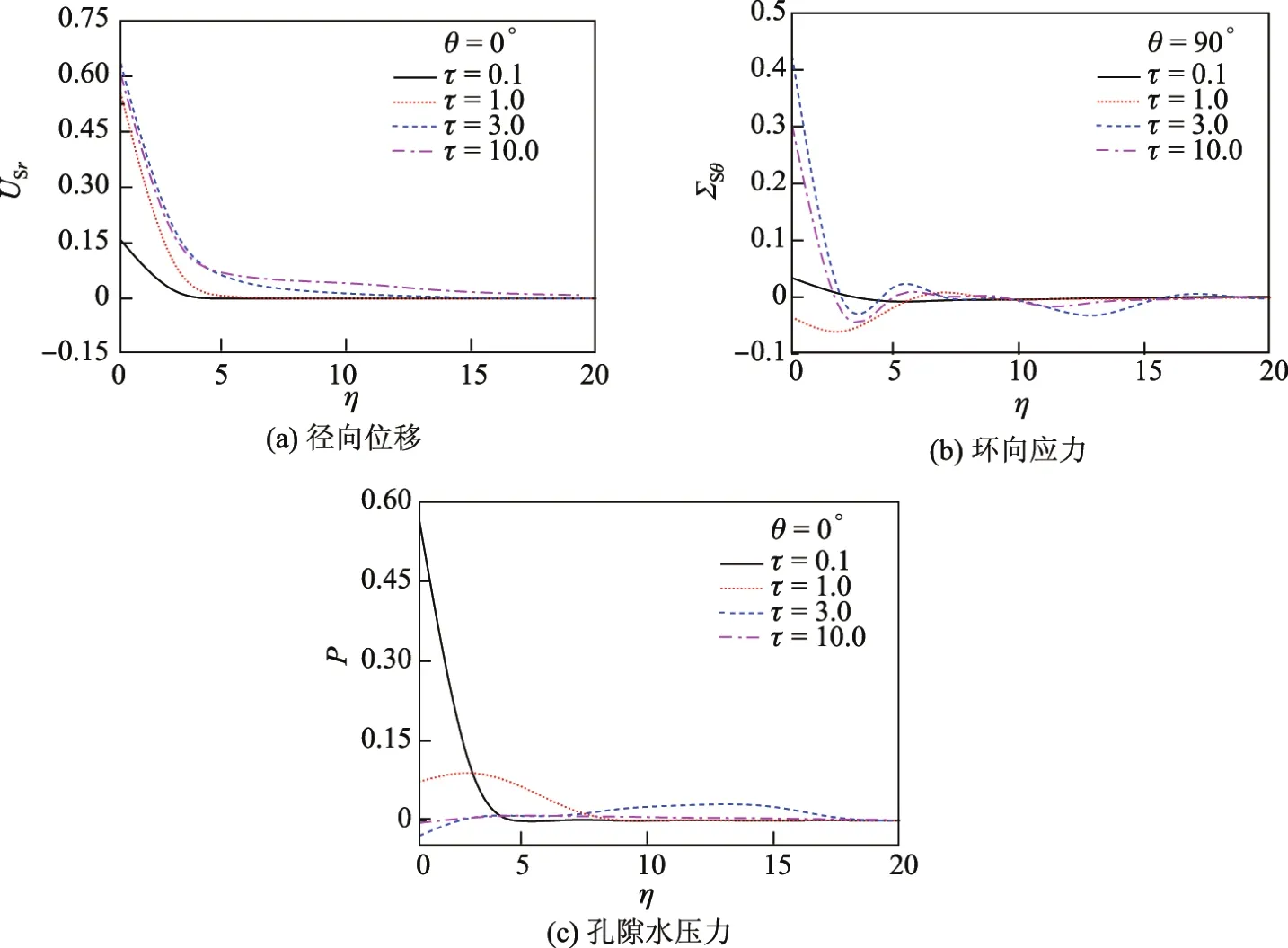
图4　突加集中常荷载作用下饱和土的动力响应沿径向的分布Fig.4　Dynamic responses of saturated soil under the constant step load along the radial position

下面以饱和土-平面应变衬砌耦合系统为例进行相关的参数分析.图5给出了当I= µL/µS取不同值(其他参数按表1选取)时,θ=0°处USr,P以及θ=90°处ΣSθ随τ的动力响应.可见,弹性衬砌刚度对土体的位移和应力响应有显著的影响,但对孔隙水压力影响较小.随着参数I的增大,土体位移、应力以及孔隙水压力幅值减小,振动减弱,即适当增加衬砌刚度可以有效减小土体的动力响应.当参数I较大时,饱和土的径向位移、环向应力和孔隙水压力几乎为0,此时外荷载基本由衬砌承担.

图6给出了h∗取不同值(其他参数按表1选取)时,θ=0°处USr,P以及θ=90°处ΣSθ随τ的动力响应.可见,类似于衬砌刚度对土体的影响,h∗对土体位移和应力响应影响显著,但孔隙水压力变化较小.随着h∗的增大,土体的位移和应力幅值减小,衬砌承担的外荷载越来越大,土体变形逐渐减小.

图7给出了M∗取不同值(其他参数仍按表1选取)时,θ=0°处USr,P以及θ=90°处ΣSθ随τ的动力响应.可见,随着M∗的增大,土体位移、应力和孔隙水压力振动幅度和周期增加,但M∗对土体位移幅值的影响相对较小.

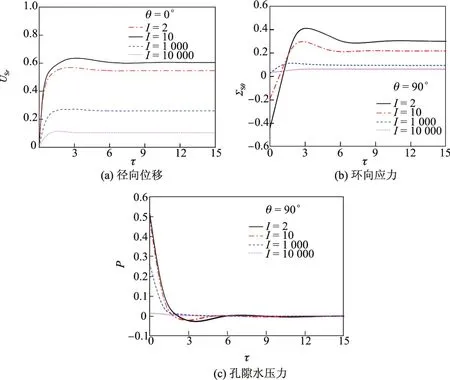
图5　I取不同值时饱和土-衬砌系统的动力响应Fig.5　Dynamic responses of saturated soil-lining system with different I

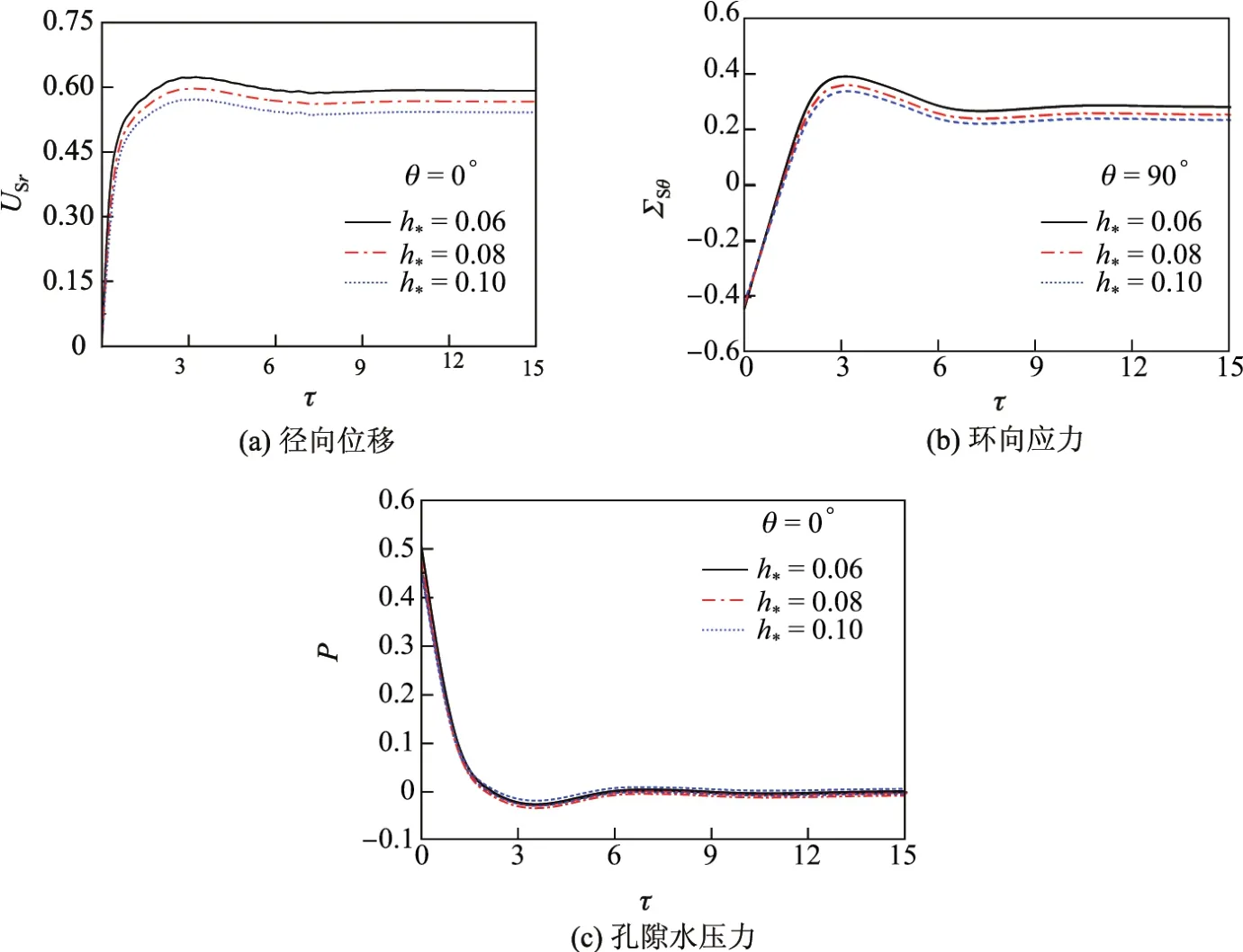
图6　衬砌厚度h∗不同时饱和土-衬砌系统的动力响应Fig.6　Dynamic responses of saturated soil-lining system with different thickness of the lining h∗

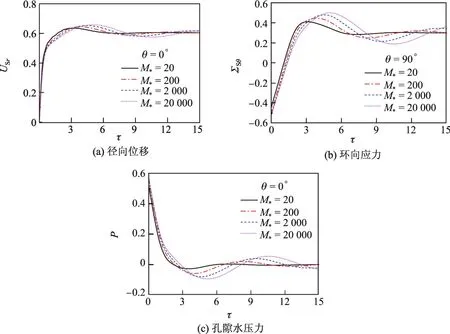
图7　M∗不同时饱和土-衬砌系统的动力响应Fig.7　Dynamic responses of saturated soil-lining system with different M∗

5　结论

本工作基于饱和土的Biot理论和弹性理论,采用Laplace变换及其数值逆变换研究了饱和土-隧道衬砌耦合系统在突加集中荷载作用下的动力响应,得到了Laplace变换域中的解析解,重点分析了土体和衬砌力学和几何参数对饱和土动力响应的影响.研究结果表明：①衬砌可明显降低土体的径向位移和环向应力,而且饱和土-壳体衬砌耦合系统模型的响应小于饱和土-平面应变衬砌耦合系统模型的响应；②突加集中荷载作用下土体的动力响应具有明显的波传播特征,且离隧道较远处的土体动力响应远小于隧道附近土体的动力响应；③衬砌刚度和厚度对土体位移和应力响应影响显著,但对孔隙水压力影响较小,适当增加衬砌刚度和厚度可以有效减小土体的动力响应；④孔隙水可压缩性对土体位移的幅值影响不大,但对应力幅值的影响较为显著,且随着孔隙水压溶性的减小,土体位移、应力和孔隙水压力振动幅度和周期增加.

[1]BIOT M A.Theory of propagation of elastic waves in a fluid-saturated porous solid.Ⅰ.Lowfrequency range[J].Journal of Acoustical Society of American,1956,28(2)：168-178.

[2]BIOT M A.Mechanics of deformation and acoustic propagation in porous media[J].Journal of Applied Physics,1962,33(4)：1482-1498.

[3]BOwEN R M.Compressible porous media models by use of the theory of mixtures[J].International Journal of Engineering Science,1982,20(6)：697-735.

[4]DEBOER R.Theory of porous media：highlights in historical development and current state[M]. Berlin：Springer-Verlag,2000.

[5]XIE K H,LIU G B,SHI Z Y.Dynamic response of partially sealed circular tunnel in viscoelastic saturated soil[J].Soil Dynamic and Earthquake Engineering,2004,24(12)：1003-1011.

[6]刘干斌,谢康和,施祖元.黏弹性饱和多孔介质中圆柱孔洞的频域响应[J].力学学报,2004,36(5)：557-563.

[7]LIU G B,XIE K H,LIU X H.Dynamic response of a partially sealed tunnel in porous rock under inner water pressure[J].Tunnelling and Underground Space Technology,2010,25(4)：407-414.

[8]杨骁,闻敏杰.饱和分数导数型粘弹性土-深埋圆形隧洞衬砌系统的动力特性[J].工程力学,2012, 29(12)：248-255.

[9]杨骁,闻敏杰.深埋圆形隧洞饱和土-衬砌简谐振动的解析解[J].上海大学学报(自然科学版),2012, 18(5)：525-530.

[10]高华喜,闻敏杰.内水压作用下粘弹性饱和土-隧洞衬砌相互作用[J].工程力学,2013,30(3)：289-296.

[11]SENjUNTIcHAI T,RAjApAKSE R K N D.Transient response of a circular cavity in a poroelastic medium[J].International Journal for Numerical and Analytical Method in Geomechanics,1993, 17(6)：357-383.

[12]杨峻,宫全美,吴世明,等.饱和土体中圆柱形孔洞的动力分析[J].上海力学,1996,17(1)：37-45.

[13]ZAKOUT U,AKKAS N.Transient response of a cylindrical cavity with and without a bonded shell in an infinite elastic medium[J].International Journal of Engineering Science,1997,35(12)：1203-1220.

[14]丁伯阳,宋新初,袁金华.饱和土隧道内集中荷载作用下振动位移反应的Green函数解答[J].工程力学,2009,26(6)：153-157.

[15]刘干斌,谢康和,施祖元.粘弹性土体中深埋圆形隧道的应力和位移分析[J].工程力学,2004,21(5)：132-138.

[16]LU J F,JENG D S,LEE T L.Dynamic response of a piecewise circular tunnel embedded in a poroelastic medium[J].Soil Dynamics and Earthquake Engineering,2007,27(9)：875-891.

[17]GAO M,WANG Y,GAO G Y,et al.An analytical solution for the transient response of a cylindrical lined cavity in a poroelastic medium[J].Soil Dynamics and Earthquake Engineering, 2013,46(3)：30-40.

[18]蔡袁强,陈成振,孙宏磊.爆炸荷载作用下饱和土中隧道的瞬态动力响应[J].岩土工程学报,2011, 33(3)：361-367.

[19]刘干斌,谢康和,施祖元.黏弹性饱和土体中圆形隧洞动力相互作用[J].浙江大学学报(工学版), 2005,39(10)：1576-1581.

[20]CRUMp K S.Numerical inversion of Laplace transforms using a Fourier series approximation[J]. Journal of the ACM,1976,23(1)：89-96.

[21]HONIG G,HIRDES U.A method for the numerical inversion of Laplace transforms[J].Journal of Computational and Applied Mathematics,1984,10(1)：113-132.

本文彩色版可登陆本刊网站查询：http://www.journal.shu.edu.cn

Non-axisymmetrical dynamic response of saturated soil and lining system with deeply embedded circular tunnel under step concentrated load

LU Jianjun,YANG Xiao
(Department of Civil Engineering,Shanghai University,Shanghai 200072,China)

Considering the interaction between soil and lining in a deeply embedded circular tunnel,the non-axisymmetrical dynamic response of a saturated soil-lining coupled system under step concentrated load was investigated.Based on the Biot’s theory and elasticity,using the Laplace transform and Fourier series,analytical expressions of displacements,stresses and pore water pressure of the saturated soil-lining system subject to step concentrated load were obtained in the Laplace transform domain under the boundary conditions of the lining and the continuity conditions on the interface between the saturated soil and lining.Numerical solutions of the dynamic responses of the saturated soil and lining system were obtained with a Crump method of the inverse Laplace transform.The influences of mechanical and geometric parameters of the soil and lining on the dynamic response of the system were analyzed.It was shown that dynamic response of the soil in adistance from the tunnel center more than 5 times of the radius was much less than that of the soil in the vicinity of tunnel.Influences of stiffness and thickness on displacements and stresses of the soil were significant,while the influences on pore water pressure were trivial. Furthermore,compressibility of pore water had stronger influence on the amplitude of the stress than that of the displacement of the soil.

saturated soil；elastic lining；concentrated load；dynamic response；Laplace transform

O 327；TU 435

A

1007-2861(2016)05-0665-15

10.3969/j.issn.1007-2861.2015.01.003

2015-02-11

国家自然科学基金资助项目(10872124)

杨骁(1965—),男,教授,博士生导师,博士,研究方向为非线性固体力学、多孔介质理论等. E-mail:xyang@shu.edu.cn