与Gamma函数有关的对数完全单调函数及其应用

孙梅

（西北大学数学学院，陕西西安710127）

与Gamma函数有关的对数完全单调函数及其应用

孙梅

（西北大学数学学院，陕西西安710127）

为了完善函数Gα，β（x）（其中参数α∈R，β≥0）及函数1/Gα，β（x）在区间（0，∞）上的对数完全单调性和相关不等式，利用Taylor展开式、Gamma函数、Psi函数的级数表达式和积分表达式研究了函数Gα，β（x）和函数1/Gα，β（x）数的对数完全单调性，将函数Gα，β（x）和函数1/Gα，β（x）对数完全单调的充分条件扩大；利用对数完全单调性得到新的不等式，并通过对特殊情形的研究，得到一个形式简单对称的双边不等式，该不等式对阶乘数之乘积与的商做出估计.

Gamma函数；对数完全单调函数；充分条件；不等式

1 引言

欧拉Gamma函数自诞生以来，作为一类特殊函数，已经被很多数学家如Gauss、Legendre、Weierstrass、Joseph Liouville关注和研究.到目前为止，Gamma函数、Psi函数、Polygamma函数［1］理论已经日趋成熟，在应用方面也达到一个新高度.它在概率论、统计学、不等式等数学分支都有着非常广泛的应用，与Gamma函数有关的完全单调函数在很大程度上推动了不等式理论的发展.以下介绍完全单调性和对数完全单调性的概念.

函数f被称作是区间I上的完全单调函数，如果f在区间I上的各阶导数都存在，且满足对任意的x∈I且n≥0，有

如果此不等式严格大于零，则称函数f在区间I上是严格完全单调函数的［2，3］.

2 主要结论及其证明

［1］Abramowitz M，Stegun I A.Handbook of Mathematical Functions with Formulas，Graphs and Mathematical Tables，National Bureau of Standards［M］.Washington：U.S.Government Printing Office，1964.

［2］Mitrinovic D S，Pecaric J E，Fink A M.Classical and New Inequalities in Analysis［M］.London：Kluwer Academic Publishers，1993.

［3］Atanassov R D，Tsoukrovski U V.Some properties of a class of logarithmically completely Monotonic functions［J］.C.R.Acad.Bulgare Sci.，1988，41（2）：21-23.

［4］Qi F，Guo B N.Complete monotonicities of functions involving the gamma and digamma functions［J］. Rgmia Res.Rep.，2004，7（1）：63-72.

［5］Widder D V.The Laplace Transform［M］.Princeton：Princeton University Press，1941/1946.

［6］Guo S，Qi F.Srivastava H M.Supplements to a class of logarithmically completely monotonic functions associated with the gamma function［J］.Applied Mathematics and Computation，2008，197（2）：768-774.

［7］Guo S，Srivastava H M.A class of logarithmically completely monotonic functions［J］.Applied Mathematics Letters，2008，21（11）：1134-1141.

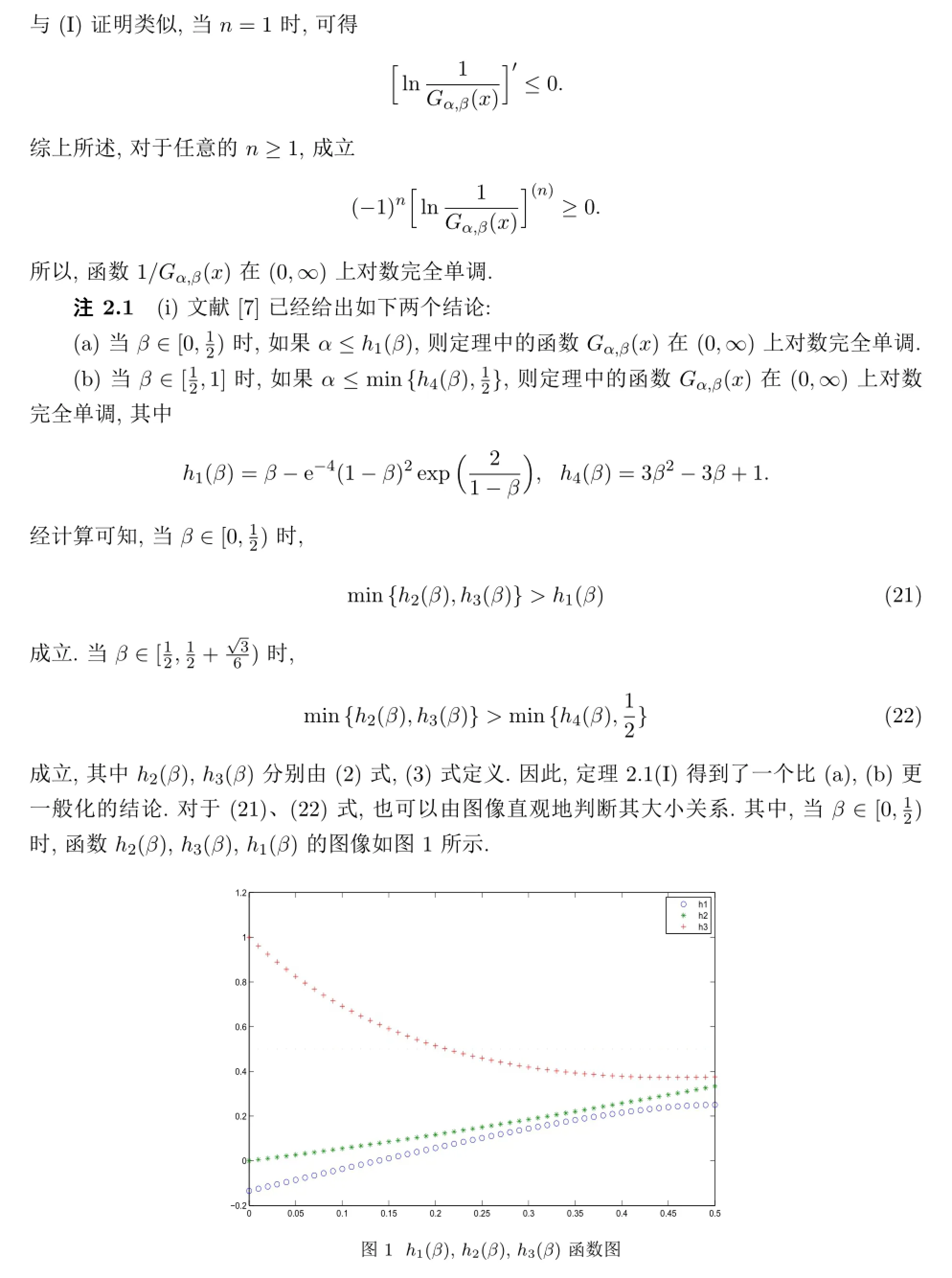
［8］Gradshteyn I S，Ryzhik（eds.）I M.Tables of Integrals，Series，and Products［M］.NewYork and London：Academic Press，2000.

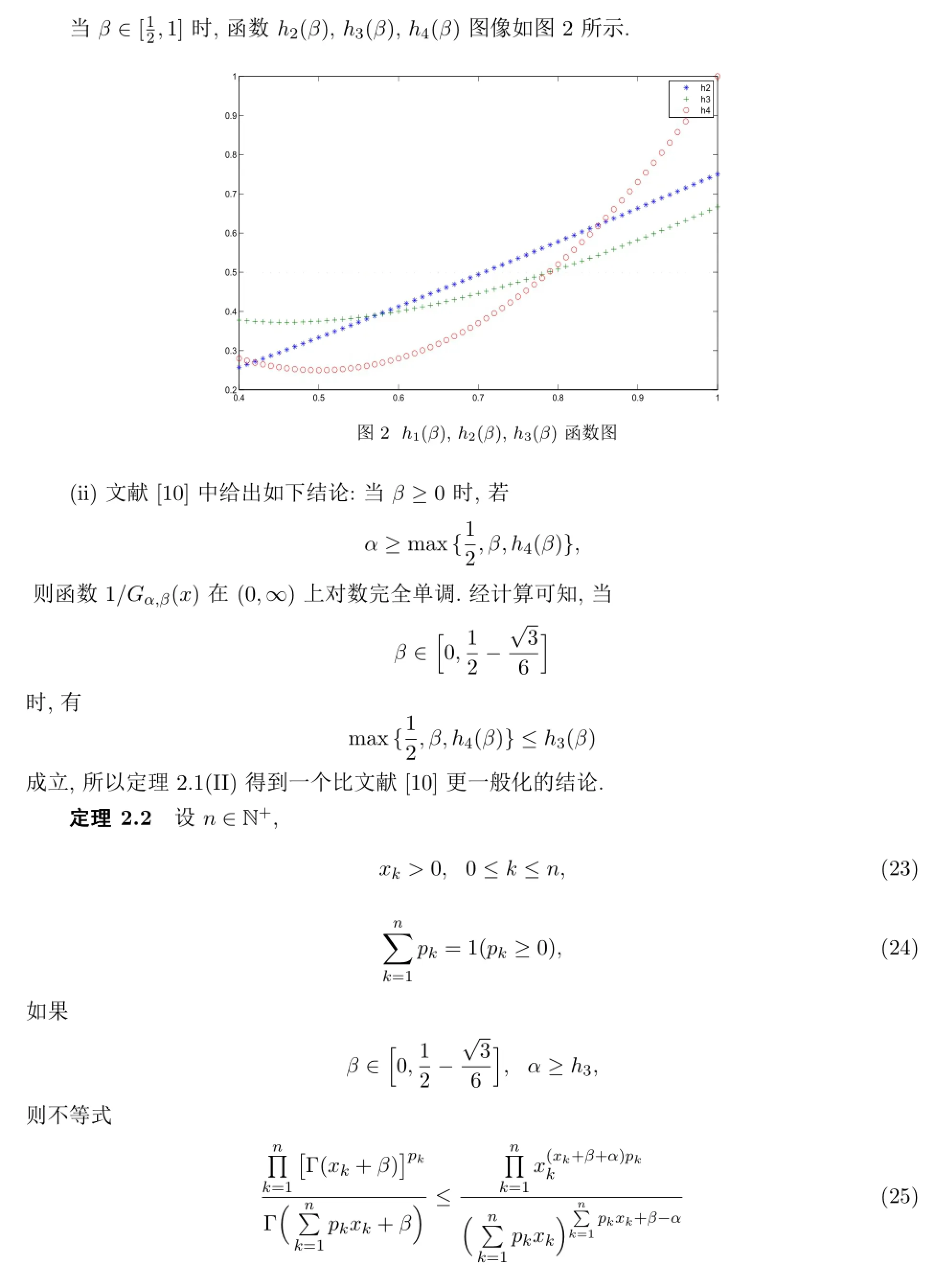
［9］Erdélyi A，Magnus W，Oberhettinger F，et al.Higher Transcendental Functions［M］.NewYork，Toronto and London：McGraw-Hill Book Company，1953.

［10］Guo S.Logarithmically completely monotonic functions and applications［J］.Applied Mathematics and Computation，2013，221（9）：169-176.

［11］Guo S，Qi F，Srivastava H M.A class of logarithmically completely monotonic functions related to the gamma function with applications［J］.Integral Transforms and Special Functions，2012，23（8）：557-566.

The logarithmically completely momotonic functions related to the Gamma function with application

Sun Mei
（School of Mathematics，Northwest University，Xi′an710127，China）

In order to improve the logarithmically completely monotonicity and related inequalities of the function Gα，β（x）（where α∈R，β≥0 are parameter）and 1/Gα，β（x）which are defined in（0，∞）.Using Taylor series expansion，the series expansion and integral expression of Gamma function and Psi function，this paper researches the logarithmically completely monotonicity of function Gα，β（x）and 1/Gα，β（x）and expands the sufficient condition.By the logarithmically completely monotonicities，a new inequality is established.Based on the research of the special circumstances，a symmetrical and concise two-side inequality，which estimates the division of factorial andis established.

Gamma function，logarithmically completely momotonic function，sufficient condition，inequality

O174.6

A

1008-5513（2016）02-0212-09

10.3969/j.issn.1008-5513.2016.02.013

2015-12-10.

陕西省自然科学基金（2010JM1017）.

孙梅（1989-），硕士生，研究方向：特殊函数论.

2010 MSC:33B15