爪极电机电磁噪声特征研究与分析

邢正坤,胡 龙

(1.河北工业大学,天津 300130;2.吉林大学,长春 132000)



爪极电机电磁噪声特征研究与分析

邢正坤1,胡 龙2

(1.河北工业大学,天津 300130;2.吉林大学,长春 132000)

电机噪声与振动是衡量电机性能的重要指标，能够影响电机的使用寿命，因此研究电磁噪声特征具有较大意义。首先，利用Maxwell 3D建立有限元分析模型，计算径向电磁力。将时域数据导入MATLAB进行频谱分析，获取电磁力波相关频域特性数据。然后，应用有限元法分析定子模态以及谐响应分析，得出电机的振动位移响应。最后将振动位移数据导入LMS Virtual.Lab声学边界元模块中计算电磁噪声频率响应。本文方法可用于电机设计阶段对电机的电磁噪声特性进行估算,进而优化电机的设计。

电磁噪声;径向电磁力;模态分析;谐响应分析;声学边界元

0 引 言

分析电机产生的振动和噪声是衡量一台电机工艺的主要手段[1]。电机振动不仅影响电机的使用寿命，而且是电机产生电磁噪声的主要因素。同时，由一系列不同频率和强度的声波无规律叠加组合成的噪声能够直接影响人的身体健康，当人处于高噪声环境或不间歇地处于噪声中会导致人的生理功能损坏，例如听力衰减[2]。

相比国外，国内对电机的振动噪声分析相对较少。文献[3]提出一种使用有限元法分析感应电机电磁力波的基本方法。文献[4]采用了有限元法计算了异步电机的径向电磁力,并探究了电磁力与电机固有频率的关系以及电机的振动特性。文献[5]应用有限元法研究了开关磁阻电机电磁力波的时域特性和频域特性。文献[6]对车用永磁电机的电磁噪声进行了研究，并对电机定子铁心的固有频率和振动特性进行了分析和研究，避免电机发生电磁共振。文献[7]使用声学边界元法计算分析了电机的声场并进行试验分析。文献[8]研究了鼠笼电机的声学边界元模型并进行声辐射计算，而且通过对比实验数据验证了其准确性。文献[9]对爪极发电机的电磁及振动特性和噪声进行了分析研究。文献[10]使用有限元法对永磁电动机的电磁振动特性和噪声进行了分析研究。

本文将一台爪极永磁发电机作为研究对象，主要研究了电机电磁力波的计算、定子结构模态分析与振动噪声计算。本论文的工作内容如下：①建立电机的电磁场有限元分析模型。利用Maxwell对电机进行气隙电磁场仿真与计算，得出电磁力波空间-时域数据；②利用MATLAB处理Maxwell仿真得出来的电磁场数据，得出电磁力波频谱、相位图。将电机定子3D模型导入Workbench模态分析模块进行固有模态分析；③利用Workbench谐响应分析模块，将电磁力加载到定子铁心各个齿面，得出电机振动位移响应;④利用LMS Virtual.Lab声学边界元分析模块，将有限元模型转化为声学模型，然后计算电机电磁噪声。

1 爪极发电机的电磁力波计算

本文分析爪极电机的相关物理结构、电磁参数如表1所示。图1为爪极电机三维模型。

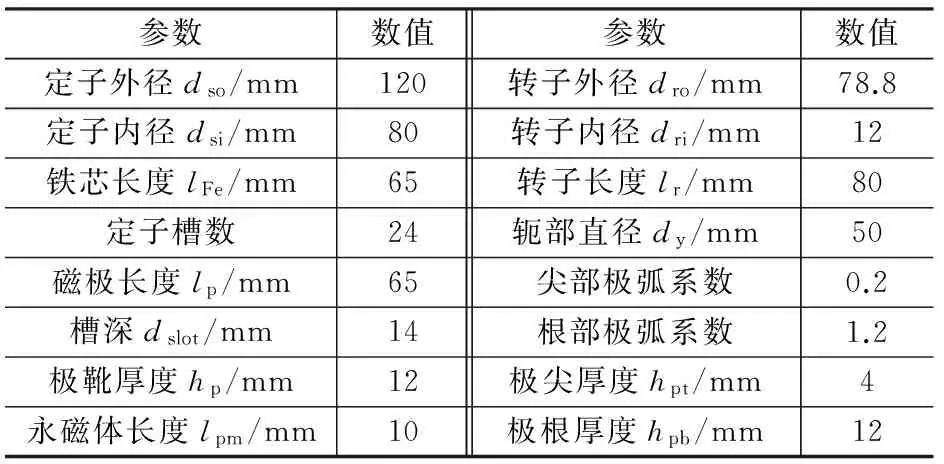
表1 爪极发电机基本参数

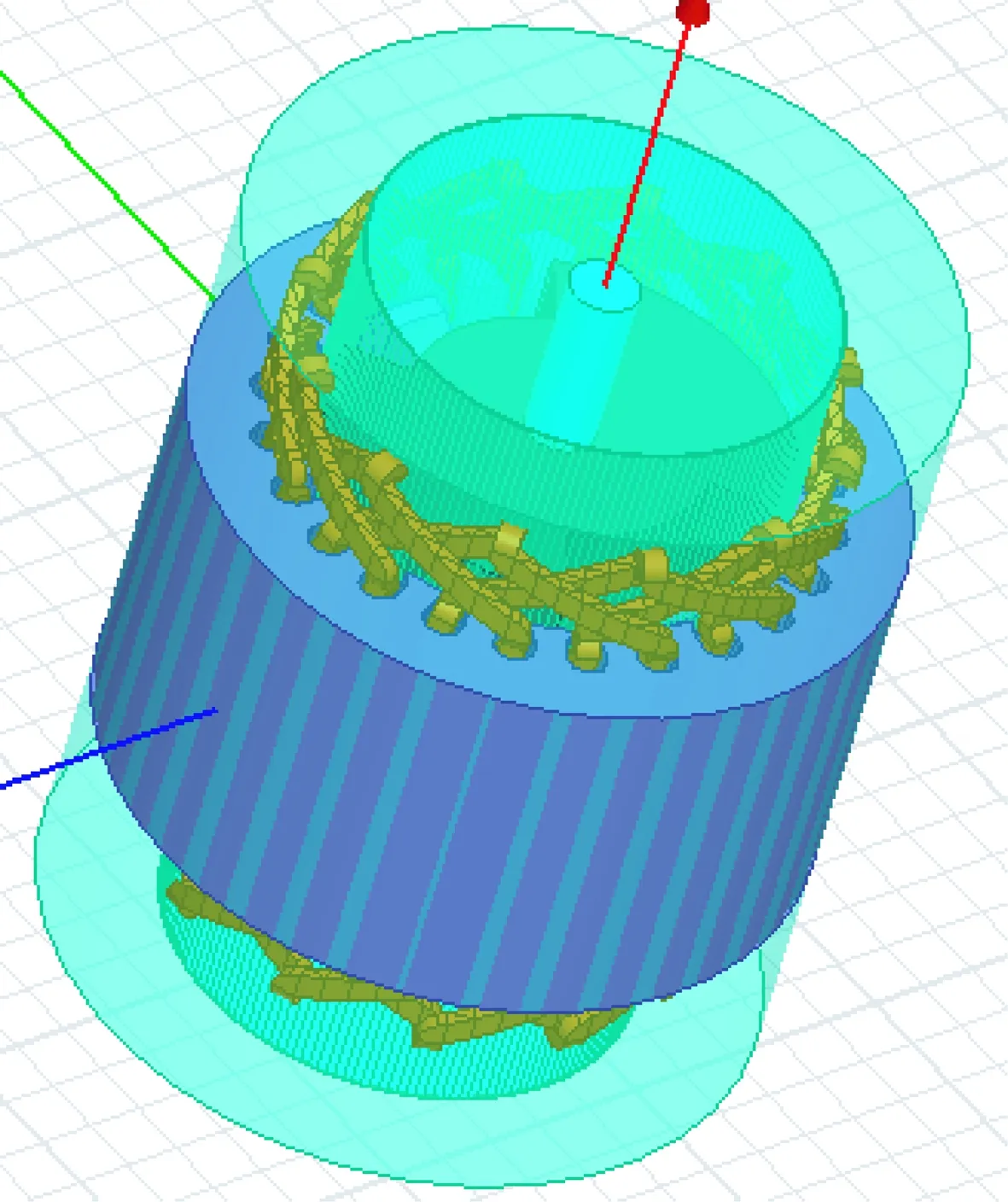
图1 爪极电机三维模型

爪极电机气隙磁场沿圆周具有径向对称性，为了降低模型计算量、缩短仿真运行时间，故而将模型简化为一对极进行计算。图2为模型简化后的定子网格划分。

图2 定子网格划分

为了保证模型的完整性，除了需要建立电机3D模型，还需要对电机设计外部连接电路。本文对外电路作了改进，采用Maxwell Circuit Editor设计了带有等效CDI点火线圈的外电路，具体电路如图3、图4所示。

其中照明电路部分参数，由运行RMxprt得到；点火线圈部分器件参数如图4所示。如此将外电路

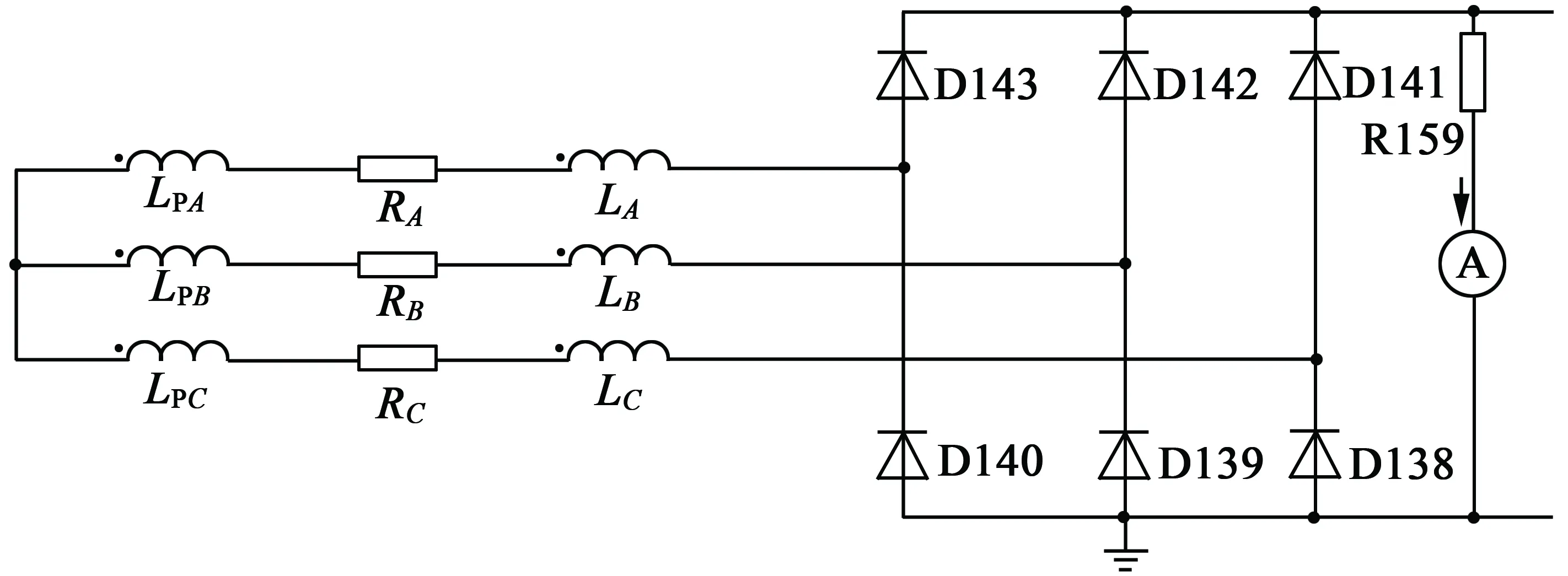
图3 外电路照明电路部分

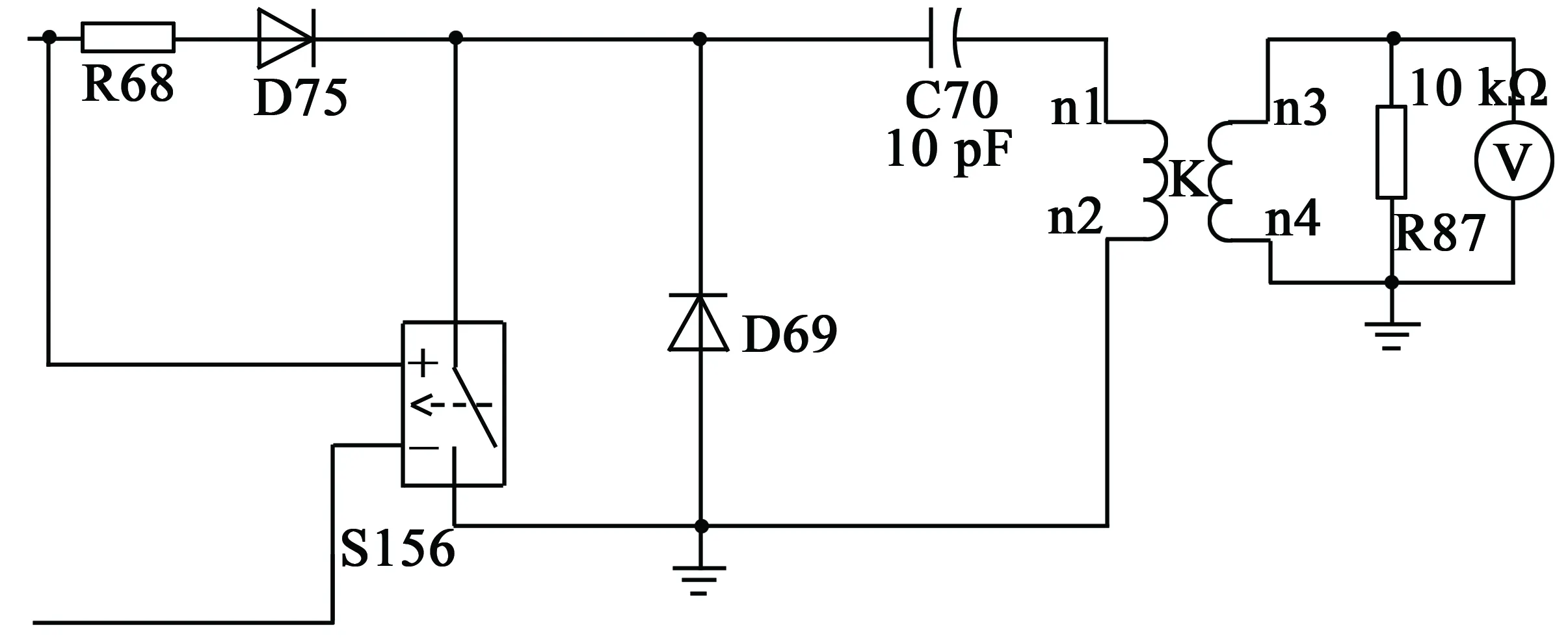
图4 外电路点火线圈部分

与三维模型相联系便得到完整的有限元模型，便可进行一步计算。

在电机定子与气隙两种材料接触面上产生的不均匀分布力,基于麦克斯韦应力张量方程，作用在爪极电机定子齿内表面上单位面积径向电磁力为:

(1)

式中：μ0为真空磁导率;Fn为径向电磁力;Bt为切向磁密;Br为径向磁密。

经过后处理得到气隙径向磁通磁密空间分布如图5所示，径向电磁力气隙的空间分布如图6所示。

图5 径向气隙磁通密度空间分布图

图6 径向气隙电磁力(单位面积)空间分布图

电磁力又是时间分布的，径向电磁力气隙的时间分布如图7所示。

图7 径向气隙电磁力(单位面积)时间分布图

径向电磁力主要作用于电机定子齿面而导致定子振动从而产生电磁振动噪声，本文在每个定子齿面上下部分分别绘制一个正方形，并求出每个齿面正方形单位面积上受到的径向电磁力，并将其等效于每个定子齿面上下部分受到的平均力，图8为定子齿面离散图[9]。

图8 定子齿面离散图

每个齿面受到的平均电磁力为Fxy,Fx2y，其中x表示X轴正方向第几个定子齿，y=1表示定子上部分、y=2表示定子下部分，x2表示X轴负方向第几个定子齿。在场计算器中输入每个定子齿面的上下部分的平均径向电磁力公式：

(2)

利用该公式对每个齿面上的正方形进行求解，则可得到Fxy,Fx2y。图9为F11的平均力波变化曲线，经计算幅值较大的电磁力波为低阶波，这里我们只取第二阶做分析，其他类似。F11二阶电磁力(单位面积)的幅值为102Pa相位为242.4°，其余平均电磁力在此不加叙述。

图9 F11电磁力(单位面积)

选择不同极槽配合作为研究对象，对比对电磁力波的影响，在原有2对极、24定子槽的基础上建立了2对极、12定子槽的爪极电机。径向电磁力如图10所示，对比图 6可知在减少定子槽数后径向电磁力峰值更大、同时具有脉冲性质，这意味着改变后的电机定子齿某一空间会承受巨大的压力，使得对电机结构的要求更高。

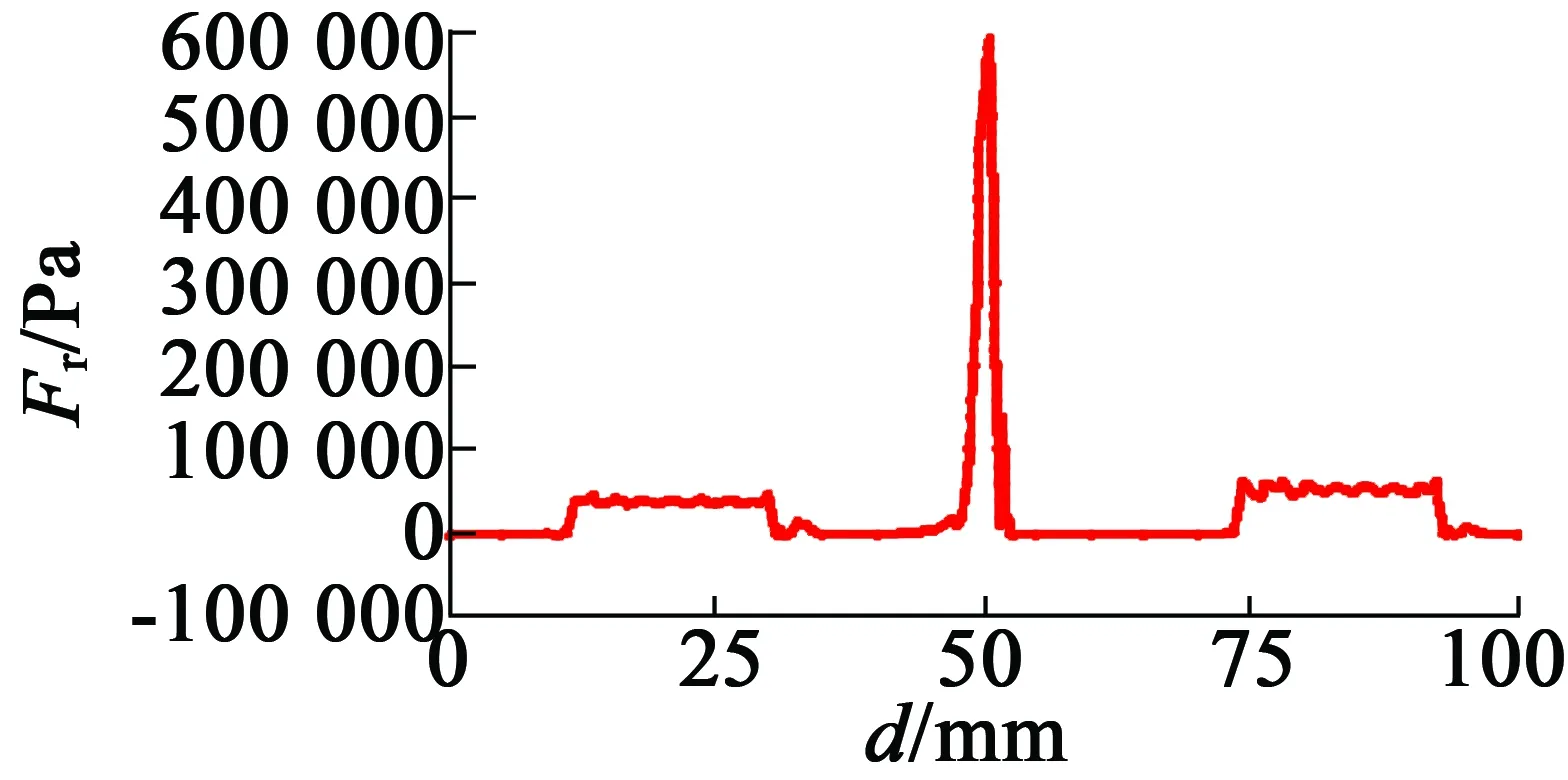
图10 径向电磁力(单位面积)空间分布图

2 爪极发电机定子固有频率模态分析

模态分析是一种研究系统振动特性的近代方法，结构系统的每一模态都具有其固定的振动模型、振动频率与阻尼比。一般物理结构的模态参数可以由数值计算或者实体试验来获得，如果采用有限元法获得模态参数则为数值模态分析，试验模态分析则是用一定的分析方法把实验获得的输入、输出数据创建联系。

通用的运动方程如式(3)[11]。

(3)

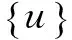
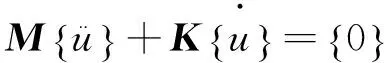
(4)

(5)

2.1 定子的模态分析

本文采用有限元法对模型进行了模态分析，其模型如图11所示。

图11 爪极电机定子铁心

因定子铁心是由硅钢片叠压而成，不能直接用硅钢片密度设置定子铁心密度，还要考虑叠片对材料密度的影响，因此定子铁心密度应设为叠压系数与硅钢片材料密度的乘积。定子铁心材料属性取值如表2所示。

表2 定子铁心材料属性表

图12为定子铁心前6阶振型云图，表3为前6阶振型对应的频率。

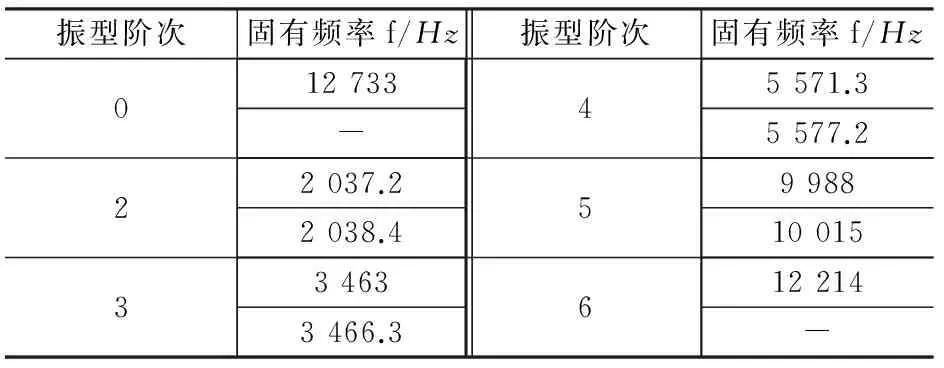
表3 定子铁心振型频率表

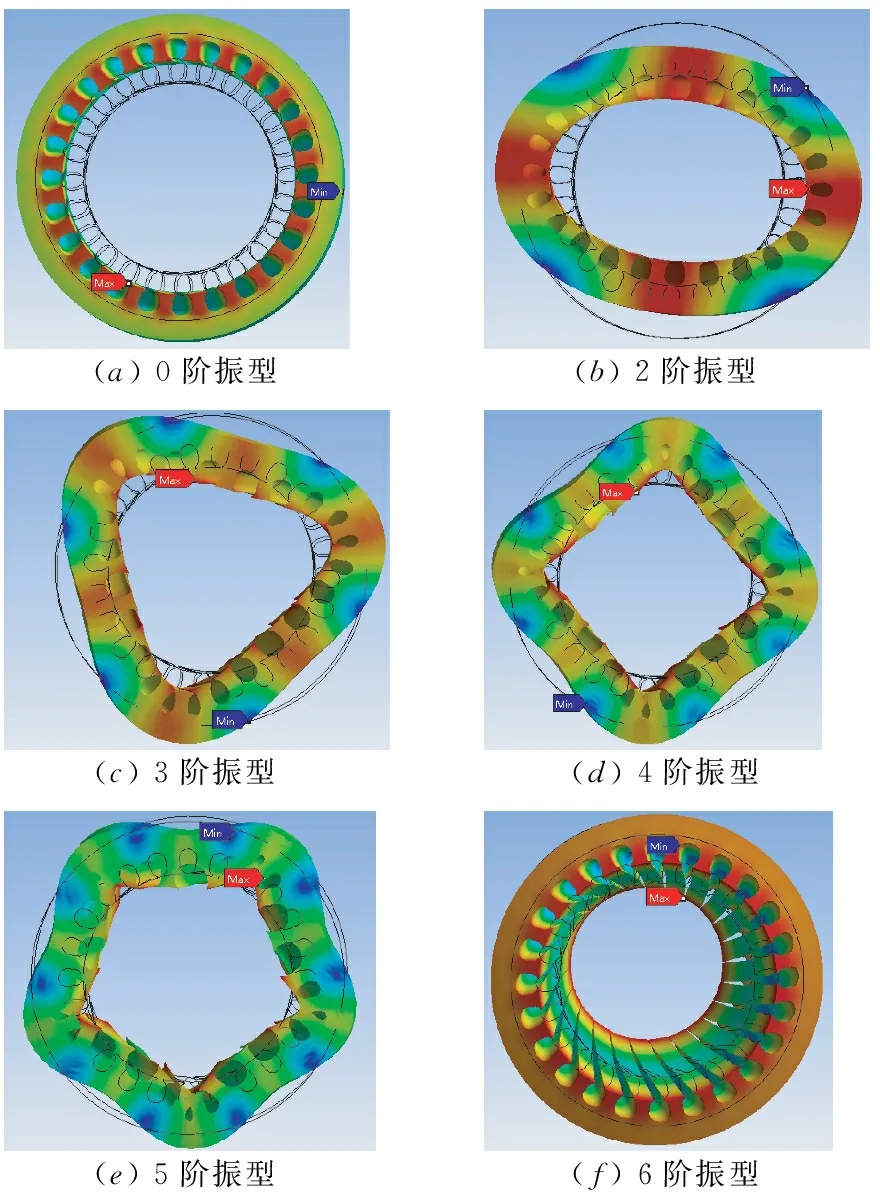
(a)0阶振型(b)2阶振型(c)3阶振型(d)4阶振型(e)5阶振型(f)6阶振型

图12 定子铁心前6阶振型云图

3 爪极发电机振动分析与噪声计算

3.1 电磁振动分析

本文应用模态叠加法求解定子的振动响应。因为在Maxwell中处理得到的是定子齿面上单位面积上受到的电磁力波，所以施加负荷为压强。利用将MATLAB中对各个齿面压强的频谱分析得到的幅值、相位数据加载到定子齿面，便完成了负荷施加，所有定子齿面施加负荷后的效果如图13所示。

图13 谐响应负荷加载

对模型分析后，求解位移、加速度谐响应结果。图14、图15分别为电机谐响应位移随频率变化图和加速度变化图。从图14可以看出，在2 500Hz到2 750Hz之间位移幅值达到峰值，从而可以预测此阶段电磁力波频率与定子结构固有频率发生了共振，这是因为与模态分析定子的固有频率2600Hz处具有振动振型相近。在2 600Hz左右位移数据最大，从而可以预测2 600Hz时的各个齿面上的电磁力波普遍幅值较大，此时电磁噪声最大。

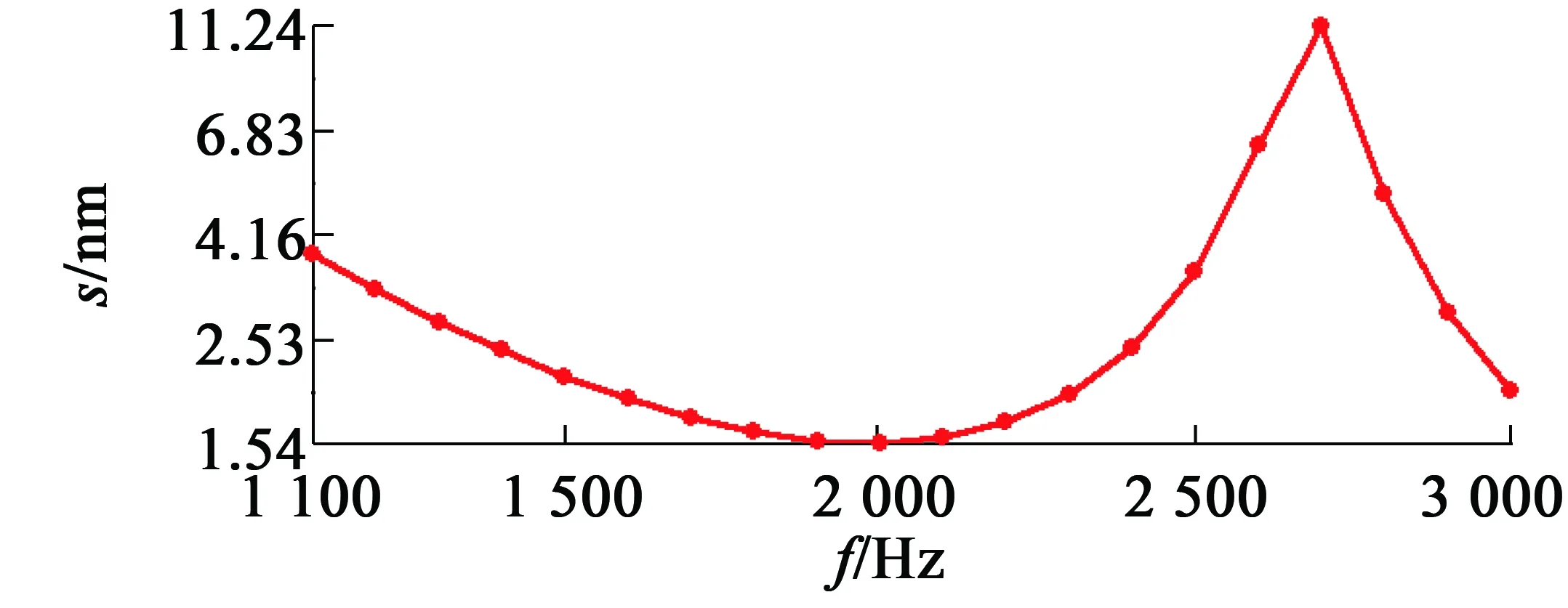
图14 谐响应位移变化曲线

图15 谐响应加速度变化曲线

3.2 电磁噪声分析

本节利用LMSVirtual.Lab仿真电机的电磁噪声特性，首先把Workbench谐响应分析有限元网格在FiniteElementModeler中转换为LMSVirtual.Lab中电机定子结构模型，其次将结构有限元网格提取出电机的声学表面网格，最后将提取的表面网格进一步粗化得到最后的声学边界元网格[9]。图16为粗化前后的电机网格模型。

因此，面对纷繁复杂、喧哗混乱的现状，人们应增强“寻获安静”的自觉。即使外部环境一时难于安静，也要努力营造宁静的小环境，像大学就应筑上一个“静”的围城，而决不可火上加油，增添杂乱。就个人来说，要不为世俗的欲望所惑，努力保持内心的明净与宁静。有名家说：“缺少了寂寞就不可能有真正的幸福。”这里的所谓“寂寞”，就是能保持自己内心的宁静，不为各种浮华的喧闹所迷惑与裹挟。

图16 粗化前后的电机网格

将谐响应分析得到的振动位移数据作为声学分析的边界条件，进行声场响应的计算，由于电机的声学边界元网格和结构网格的单位尺寸、单元密度与节点坐标都不一致，故而需要对导入的振动位移数据进行数据转移，建立起振动数据与有限元网格的对应关系。之后，需要添加一个声学网格，并且由于实际上在半消音室中测量电机噪声时在地面上有光滑的地板反射声音，故而在仿真时需要在电机下方添加一个全放射平面，如图17所示。再对一些基本的声学分析项进行定义便可以计算电机声场响应(设置边界条件等)，并且通过在场点网格上设置一系列场点。通过场点计算后便可以观察这些场点的声压随频率的变化曲线图。

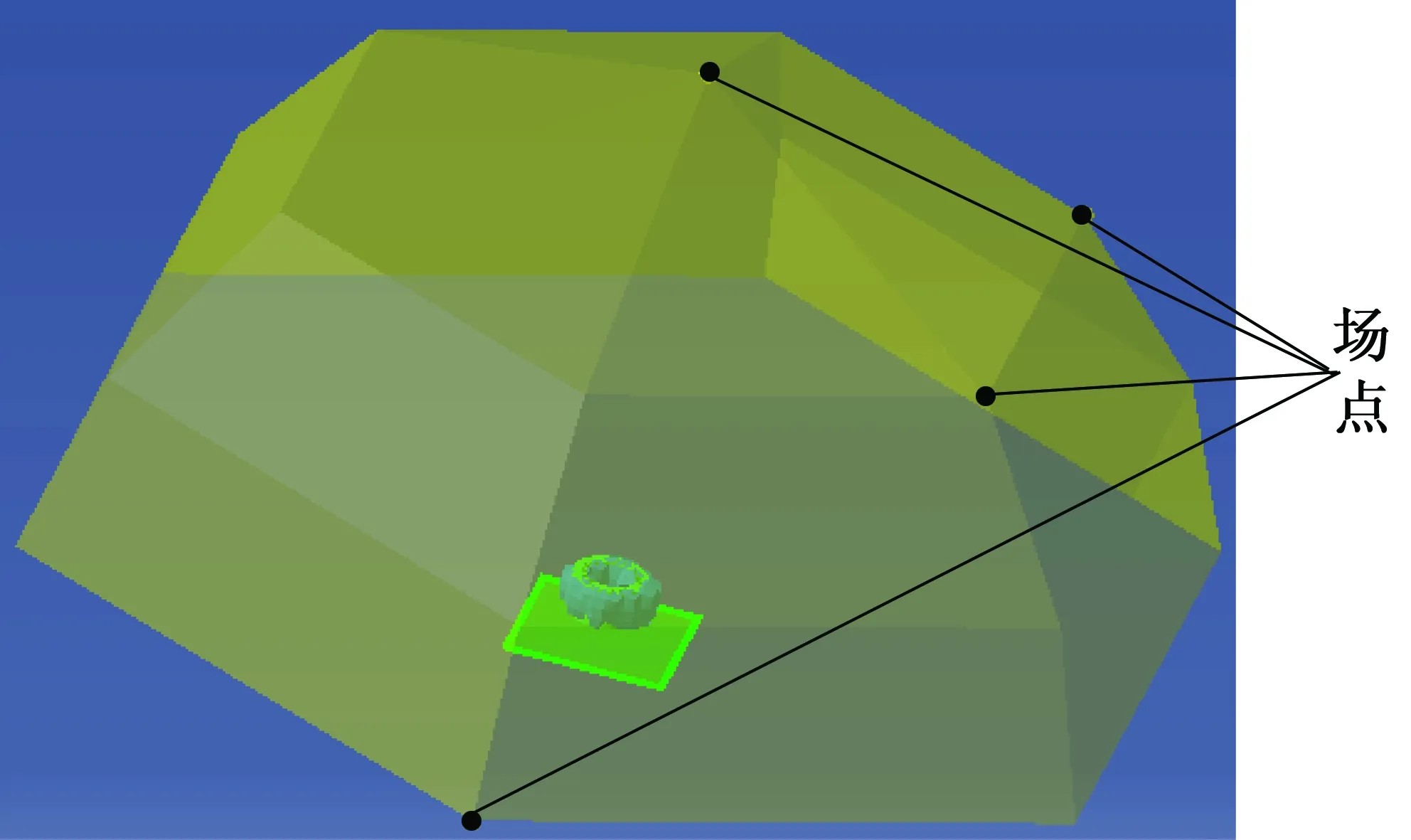
图17 发电机电磁噪声仿真模型

通过仿真计算，图18为场点网格上4个场点的变化曲线。从图18可以看出发电机产生的电磁噪声声压级在2 600Hz共振频率附近达到峰值，而一旦越过此峰值声压级成单调衰减，也就是说电机产生的电磁噪声为低频声波，且减小电磁噪声可从以下部分入手：

(1)由于各场点的声压级不同，因此可以将易受声波干扰的物体定向安装在特定的位置，使得其受到的声压辐射最小。

(2)在发电机升速的过程中能产生使电机发生共振的电磁力的转速时,以最短的时间越过此转速。

(3)添加适当的阻尼器件，使得声压级快速衰减。

图18 场点声压级变化曲线

改变定子槽数的电机采用同样的处理后得到同频率段范围内的电磁噪声声强变化如图19所示。

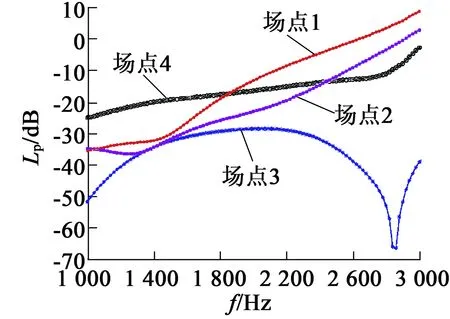
图19 不同槽数场点声压级变化曲线

从图19可得改变极槽配对后电机电磁噪声声压级明显降低，从而有效降低低频范围内的电机噪声。此外，由于改变极槽配对后定子结构的固有频率显著提升，而高阶电磁力波的频率增长速度又明显慢于固有频率的增长，因此可以说适当的改变极槽配对能够有效地改变发电机产生的电磁噪声。

4 结 语

(1)软件建立了完整的三维电磁场分析模型，得到爪极发电机的气隙磁场及径向电磁力波，求得定子齿面上下部分的平均电磁力的幅值、相位和阶次。

(2)对定子固有模态进行了计算。基于模态叠加将径向电磁力加载到相应的定子齿面上做谐响应分析，研究了发电机的振动变形情况。2 600 Hz左右位移数据最大，可以预测2 600 Hz时的各个齿面上的电磁力波普遍幅值较大，此时电磁噪声最大。2 600 Hz和定子固有频率相近时噪声最大。

(3)对电机电磁噪声原理理解基础上，通过对外电路增加点火线圈改变电磁力特性，以及适当地改变极槽配对，能够有效地改变发电机产生的电磁噪声。

(4)对电磁噪声进行了声场辐射分析。可以在电机设计阶段预估出电磁噪声性能,进而优化电机设计。

[1] 陈永校,诸自强,应善成.电机噪声的分析与控制[M].杭州:浙江大学出版社,1987.

[2] 舒波夫.电机的噪声和振动[M].北京:机械工业出版社,1980.

[3] ISHIBASHI F,NODA S,MOCHIZUKI M.Numerical simulation of electromagnetic vibration of small induction motors[J].IEE Proceedings:Electric Power Applications,1998,145(6):528-534.

[4] MORI D,ISHIKAWA T.Force and vibration analysis of induction motors[J].IEEE Transactions on Magnetics,2005,41(5):1948-1951.

[5] ANWAR M N,HUSAIN I.Radial force calculation and acoustic noise prediction in switched reluctance machines[J].IEEE Transactions on Industry Applications,2000,36(6):1589-1597.

[6] 杨萍,代颖,黄苏融,等.基于有限元法的车用永磁同步电机电磁噪声的评估[J].电机与控制应用,2012,39(9):33-37.

[7] 尚修敏.车用交流发电机电磁噪声仿真分析[D].成都:西南交通大学,2013.

[8] 王荀,邱阿瑞.鼠笼异步电动机电磁噪声的仿真分析[J].微电机,2011，44(7):15-19 .

[9] 马龙.某型车用发电机电磁噪声的仿真分析[D].锦州:辽宁工业大学,2014.

[10] 何鹄环.永磁有刷直流电动机电磁振动与噪声的分析[D].上海：上海交通大学,2012.

[11] 王天煜,王凤翔.大型异步电机结构振动特性的研究[J].机械强度，2009，31(1)：140-143.

Study and Analysis of Electromagnetic Noise Characteristics of Claw Pole Motor

XINGZheng-kun1,HULong2

(1.Hebei University of Technology,Tianjin 300130,China;2.Jilin University,Changchun 132000,China)

Motor noise and vibration as the important indicators of a motor performance, can affect the using time limit of the motor, so making the study characteristics of the electromagnetic noise is quite significant. First of all,using the Maxwell 3D finite element analysis model was established, and calculating the radial electromagnetic force, the spectrum analysis transforms the data into MATLAB to obtain the electromagnetic wave frequency domain characteristics of relevant data.Then, the finite element method was used to analyze the stator modal and harmonic response analysis, the vibration displacement response of the motor were obtained. Finally the vibration displacement data import LMS Virtual. Lab acoustic boundary element in the module calculating electromagnetic noise frequency response.The method can be used in the design of motor phase estimation of electromagnetic noise characteristics of the motor, and then optimize the design of the motor.

electromagnetic noise; radial electromagnetic force; modal analysis; harmonic response analysis; acoustics boundary element

2015-06-23

河北省高等学校科学研究技术研究重点项目(ZD2016045)

TM35

A

1004-7018(2016)07-0017-04

邢正坤( 1988-) ，男，硕士研究生，研究方向为电机振动噪声、电力拖动。