基于改进粒子群算法的BLDCM分数阶速度控制器的研究
2016-12-21金鹏,李晶
金 鹏,李 晶
(辽宁工程职业学院 ,铁岭 112008)
基于改进粒子群算法的BLDCM分数阶速度控制器的研究
金 鹏,李 晶
(辽宁工程职业学院 ,铁岭 112008)
分数阶PIλDμ控制器具有5个控制参数,相比于传统PID控制器具有更高的控制精度及灵活度。将分数阶PIλDμ控制器应用于BLDCM调速系统可有效提高其性能指标。但由于增加了控制参数λ和μ,参数整定难度也相应提高。提出一种通过改进的粒子群算法对分数阶PIλDμ控制器参数寻优的方法,并引入自适应权重策略和混沌局部搜索策略来克服普通粒子群算法容易陷入局部最小解及收敛速度慢的不足。仿真和系统实际运行效果都证明该方法的可行性。
BLDCM;分数阶PIλDμ;参数整定;粒子群算法
0 引 言
由于PID具有编程简单、使用方便、实用性强等优点,所以多年来PID控制器一直是主要的过程控制器;但PID控制也具有反应速度不快、超调较大、控制精度不高、控制灵活度不强、需要精确控制模型等缺点。由于无刷直流电动机(以下简称BLDCM)是一个非线性、多变量、时变的系统,难以建立精确模型,所以普通PID控制效果差强人意[1]。模糊算法及一些人工智能算法虽然可以对PID参数自整定,做出近乎完美的仿真曲线,但在实际的电机过程控制中,3个最优的PID参数往往不能使电机获得最优的动态性能。分数阶PIλDμ引入了积分阶次λ和微分阶次μ,并且λ和μ可以是大于0的任意实数,使得控制灵活度大大提高,但同时也增加了参数整定难度。文献[2-3]提出利用模糊算法来自整定分数阶PIλDμ的参数,由于目前没有成熟的λ和μ的经验规则,所以文献中只对Kp,Ki,Kd自适应调节,λ和μ则手动精调。
由于分数阶PIλDμ的5个参数是相互关联的,本文提出通过粒子群算法(PSO)来对分数阶PIλDμ控制器的5个参数同时自适应寻优。针对PSO存在容易陷入局部最小解,收敛速度慢等不足,利用自适应权重和混沌局部搜索两种策略使算法跳出局部最小解、加速算法收敛。最后通过MATLAB仿真和实验测试来验证算法的可行性。
1 FOPID控制器及其整数阶近似
Podlubony在分数阶微积分基础上提出了分数阶PIλDμ(fractional-order PID,FOPID),FOPID的微分方程[4]:
(1)
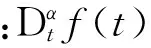
根据分数阶微积分的Laplace变换:
(2)
得FOPID的传递函数:
(3)
当λ=1,μ=1时,式(3)变成:
(4)
因此,可以说PID控制器是FOPID控制器的特例。由于λ和μ可以取大于0的任意实数,因此FOPID控制器具有无限维特性,比传统的PID控制器具有更高的灵活度。
但正是由于FOPID具有无限维特性,因此难以应用于实际的过程控制中,目前广泛采用的方法是利用Oustaloup滤波算法[5]在有限频域段(wb,wh)内,通过频域拟合的方法对微积分算子sα近似成整数阶传递函数的形式,Oustaloup滤波算法如式(5)。
(5)
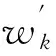
上式中,α为微分阶次;N为滤波器阶次。但随着阶次N的增高,Oustaloup滤波算法在高频区域的近似效果并不好[6-7],设FOPID控制器传递函数:
滤波器阶次为4,频段(10-4,104),Gc1(s)的Oustaloup滤波算法频率特性如图1所示。
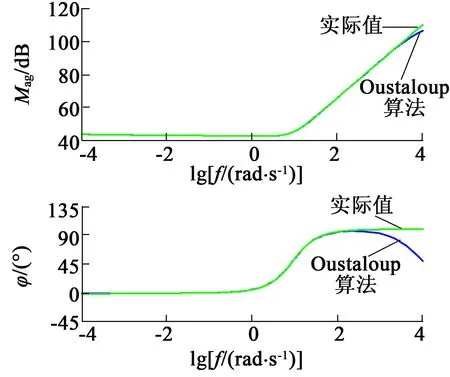
图1 Oustaloup频率特性
文献[8]提出一种改进的Oustaloup滤波算法,公式如下:
(6)
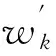
相同的滤波器阶次、频率范围下,Gc1(s)的改进Oustaloup滤波算法频率特性如图2,可见,改进Oustaloup滤波算法在高频区域的近似效果很好。由于篇幅有限,这里没有列出近似后的整数阶Gc1(s)传递函数。

图2 改进的Oustaloup频率特性
2 ACPSO-FOPID控制器设计
FOPID控制器共有5个参数Kp,Ki,Kd,λ,μ需要调节,本文采用改进的粒子群算法对5个参数同时进行寻优。针对标准粒子群算法(PSO)对复杂问题寻优求解时容易出现早熟、精度较低、迭代后期粒子多样性迅速衰减、收敛速度变慢等问题,提出一种自适应混沌粒子群算法(ACPSO),其基本思想是将参数自适应整定策略和基于改进的Tent映射的混沌局部搜索策略融入到PSO算法中,进而形成ACPSO-FOPID控制器。
2.1 惯性权重自适应调整策略
标准PSO算法可以描述为:在n维求解空间,第i个粒子根据粒子个体极值Pi(pi,1,pi,2,…,pi,n)与种群全局极值Pg=(pg,1,pg,2,…,pg,n)动态调节自身的位置Xi=(xi,1,xi,2,…,xi,n)和速度Vi=(vi,1,vi,2,…,vi,n)。求解前需初始化种群中各粒子的位置及速度,当第t次迭代时,粒子按式(7)与式(8)更新下代的速度和位置:
(7)
(8)
式中:w为惯性权重,代表寻优过程粒子自身速度的惯性;c1,c2为学习因子,其中c1代表粒子自身经验的学习能力,c2代表粒子对于群体经验的学习能力;rand是(0,1)之间的随机数;pbest是个体最优值经历的最好位置;gbest是种群经历的历史最优位置。
惯性权重w关系到粒子群算法的寻优速度。较大的惯性权重w寻优速度较快,有利于全局快速搜索;较小的惯性权重w寻优速度较慢,有利于局部精细搜索、加快收敛。本文采用的自适应惯性权重如下式:
(9)

2.2 混沌搜索
鉴于混沌变量在一定范围内具有随机性、遍历性和规律性的特点,将混沌算法和粒子群算法相结合,通过将寻优搜索过程对应为混沌轨迹的遍历过程,可以使寻优过程具有避免粒子陷入局部极小解的能力。不同的混沌映射算子对混沌寻优过程有很大的影响,文献[9]论证了Tent映射具有更好的遍历均匀性和更快的迭代速度,Tent映射可以表示成如下形式:
(10)
式中:k为混沌迭代次数,k=0,1,…,Nmax。当经过多次迭代后,Tent 映射趋会向于{0,0.25,0.5,0.75}的不动点或出现4的小周期{0.2,0.4,0.6,0.8},导致Tent 映射随机、遍历性能下降,当出现这两种状况时,对Tent 映射进行改进,按式(11)重新赋值。
(11)
基于Tent 映射的混沌搜索步骤如下:
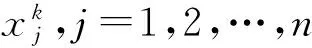
(12)
式中:xmax,j和xmin,j分别为j维变量的搜索上下界限。
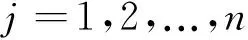
(13)
2.3 基于ACPSO算法的参数寻优
利用改进的自适应混沌粒子群算法(ACPSO)对FOPID的5个参数进行寻优的过程就是将参数Kp,Ki,Kd,λ,μ看作是粒子群中的5个粒子,在搜索空间中搜寻这5个粒子的最优位置。
ACPSO-FOPID控制器设计的主要步骤如下:
(1) 粒子群中各类参数初始化:种群规模N,维数n,搜索空间上下限Ud和Ld,学习因子c1和c2,算法最大迭代次数Tmax等参数。
(2) 应用改进Tent混沌映射算法初始化粒子的位置和速度,产生FOPID需整定的5个参数(Kp,Ki,Kd,λ,μ)的位置序列。
(3) 调用系统模型,根据ITAE指标计算各粒子的个体适应度fi,并保存个体最优位置Pi及群体最优位置Pg。
(4) 按照式(7)和式(8)对粒子速度和位置进行更新。按式(9)对惯性权重自适应更新,并计算更新后每个粒子最优位置Pi和全局最优位置Pg。
(5) 根据下式计算群体的适应度方差σ2:
(14)
式中:N为种群规模,f为归一化因子,其表达式:
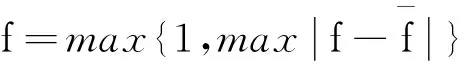
(15)
若σ2小于阈值即认定当前粒子群陷入局部极小解,则转步骤(6),否则转步骤(7)。
(6) 对个体适应度较好的20%的粒子执行混沌局部搜索。
(7) 算法达到最大迭代次数,寻优结束,返回全局最优值。
3 仿真及实验
为验证ACPSO-FOPID控制器的可行性,本文分别在仿真环境和实验平台对算法进行了测试。
3.1 建模仿真
在MATLAB/Simulink环境下,根据BLDCM的控制模型建立BLDCM双闭环控制系统仿真模型,如图3所示。其中转速控制器的ACPSO算法采用m语言编写。
对ACPSO-FOPID算法仿真5次,取最优结果作为控制器的参数Kp,Ki,Kd,λ,μ。电机参数设置如下:额定电压UN=24 V;额定转矩TN=0.23 N·m;额定转速nN=3 000 r/min;定子相绕组电阻R=0.6Ω;定子相绕组有效电感为L-M=1.45mH;转
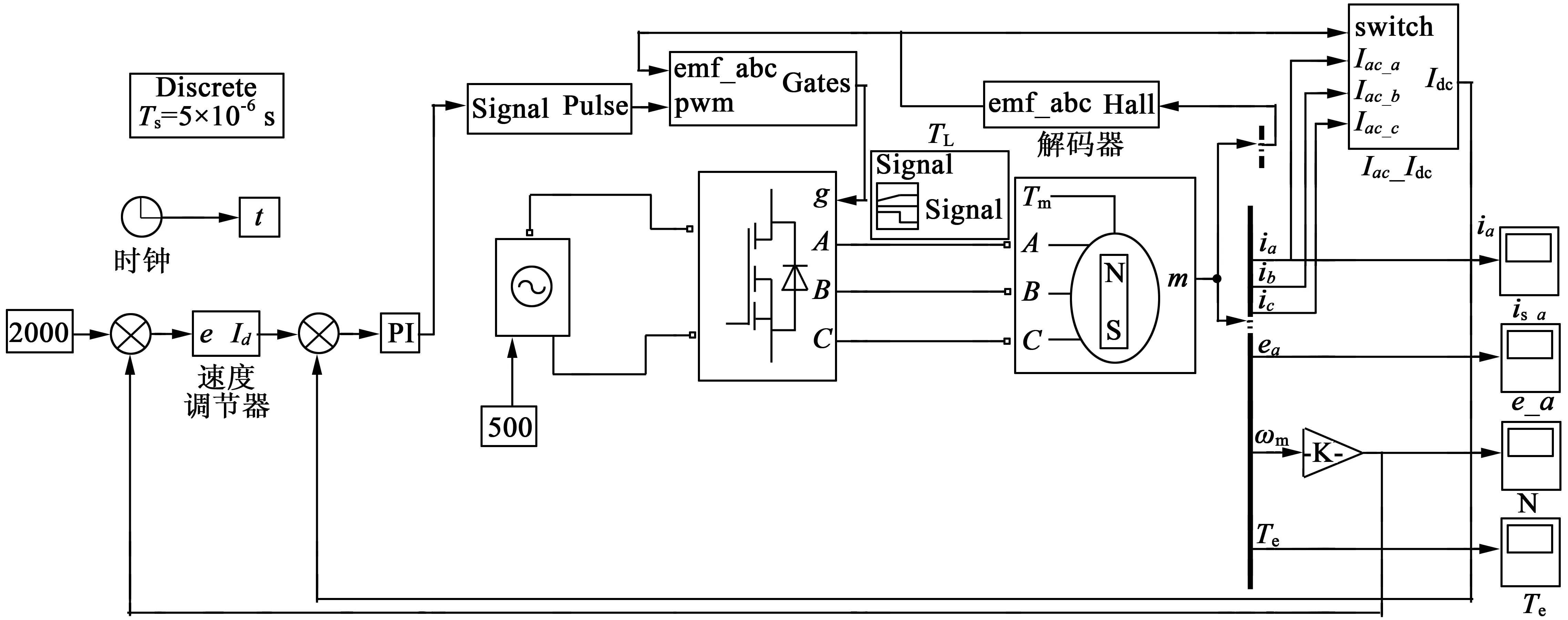
图3 BLDCM双闭环控制系统仿真模型
动惯量为J=0.001 05 kg·m2;极对数n=5。粒子种群参数设置如下:种群规模N=100,维数n=5,最大迭代次数Tmax=100,学习因子c1=2,c2=2,搜索空间上限Ud=[40 40 40 2 2]、下限Ld=[0 0 0 0 0]。通过5次仿真得到控制器最优参数:Kp=35.26,Ki=0.025,Kd=2.63,λ=0.56,μ=0.72。
图4为PID、PSO-FOPID、ACPSO-FOPID 3种算法下的转速相应曲线,图5为PSO、ACPSO两种算法的适应度收敛曲线,表1为3种算法时域指标。
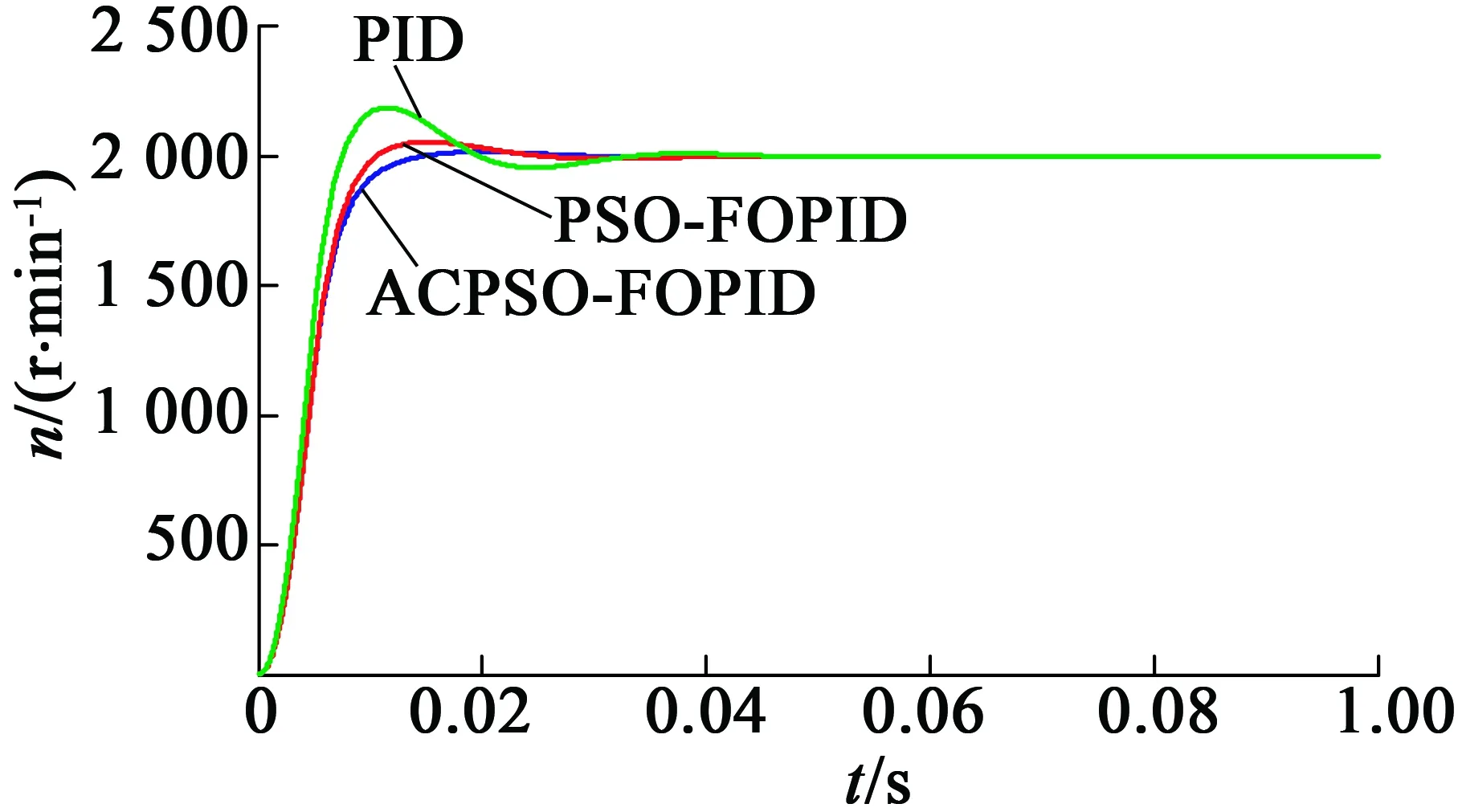
图4 3种算法转速相应曲线对比
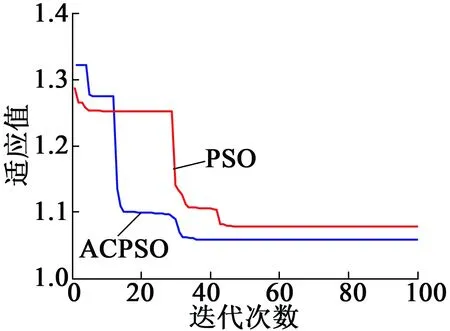
图5 ACPSO算法与PSO算法适应度收敛曲线
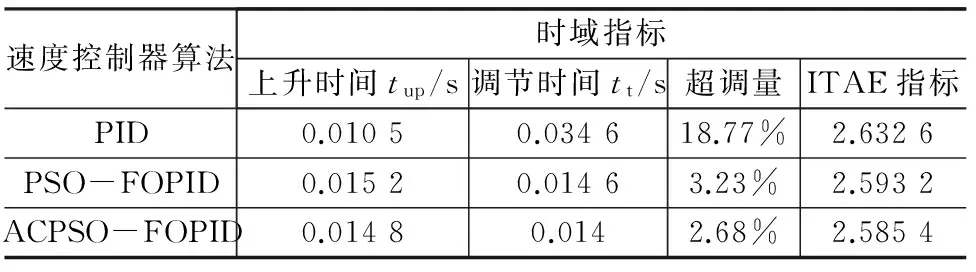
表1 3种算法时域指标
通过上面的图、表可以看出,ACPSO算法能有效避免早熟现象产生,其收敛速更快。ACPSO-FOPID相比其它2种算法具有更快的反应速度、更小的超调量、更高的控制精度等动态性能。
3.2 实验测试
最后,在BLDCM测试平台进行样机测试,实验平台采用北京君合泰科技的虚拟仪器测控实验箱,其内置的NI PCI-6221数据采集卡具有2路16位模拟输出通道 (833 kS/s),测试对象为智创92BL型BLDCM。测试时对电机加载转矩0.2 N·m,分别将PSO算法和ACPSO算法寻优得到的最优参数输入FOPID控制器中,并与普通PID控制器一起做转速对比实验。在LabVIEW虚拟示波器中分别显示了给定转速200 r/min时的转速响应曲线,如图6~图8所示。
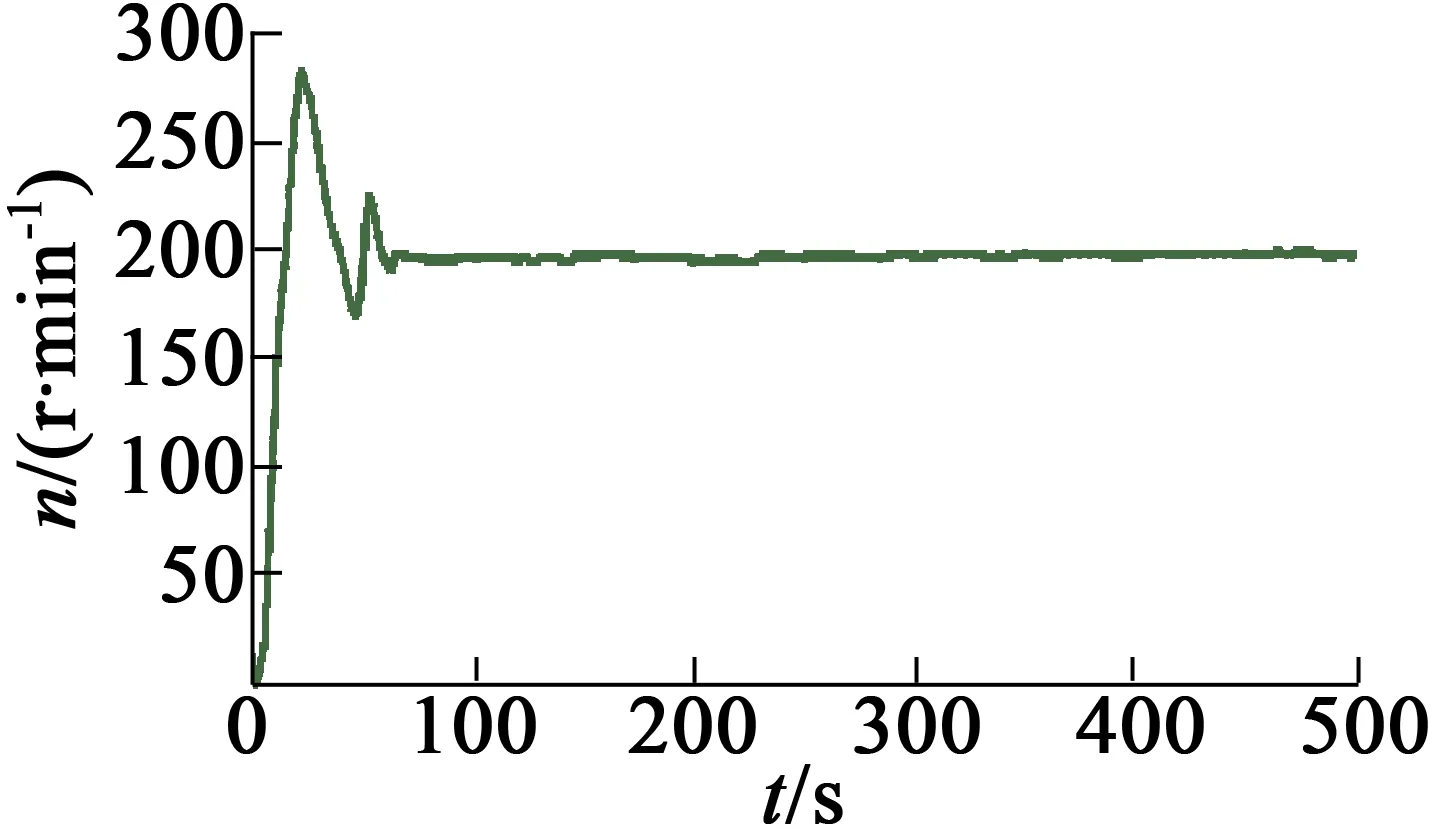
图6 PID算法转速响应曲线
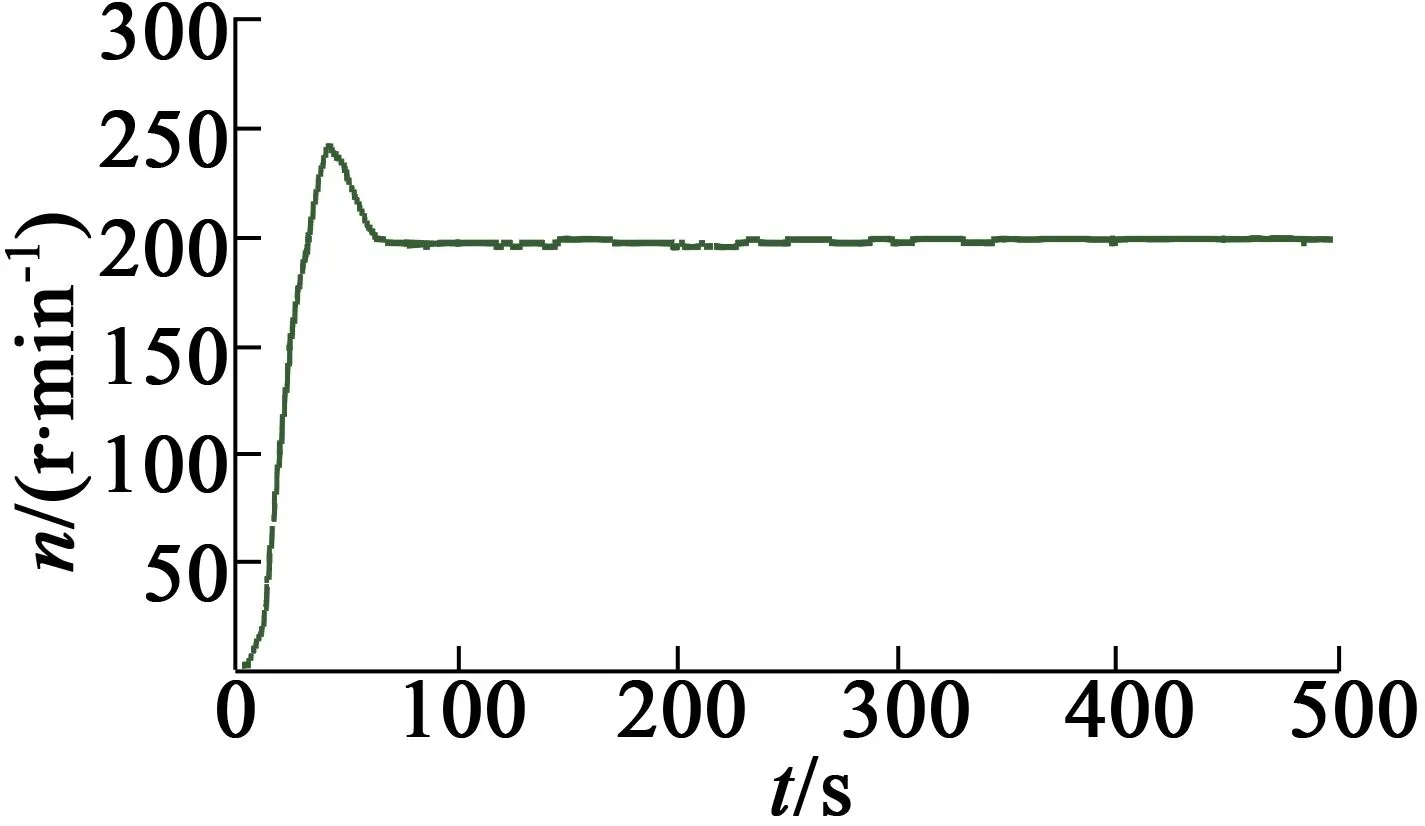
图7 CPSO-FOPID算法转速响应曲线
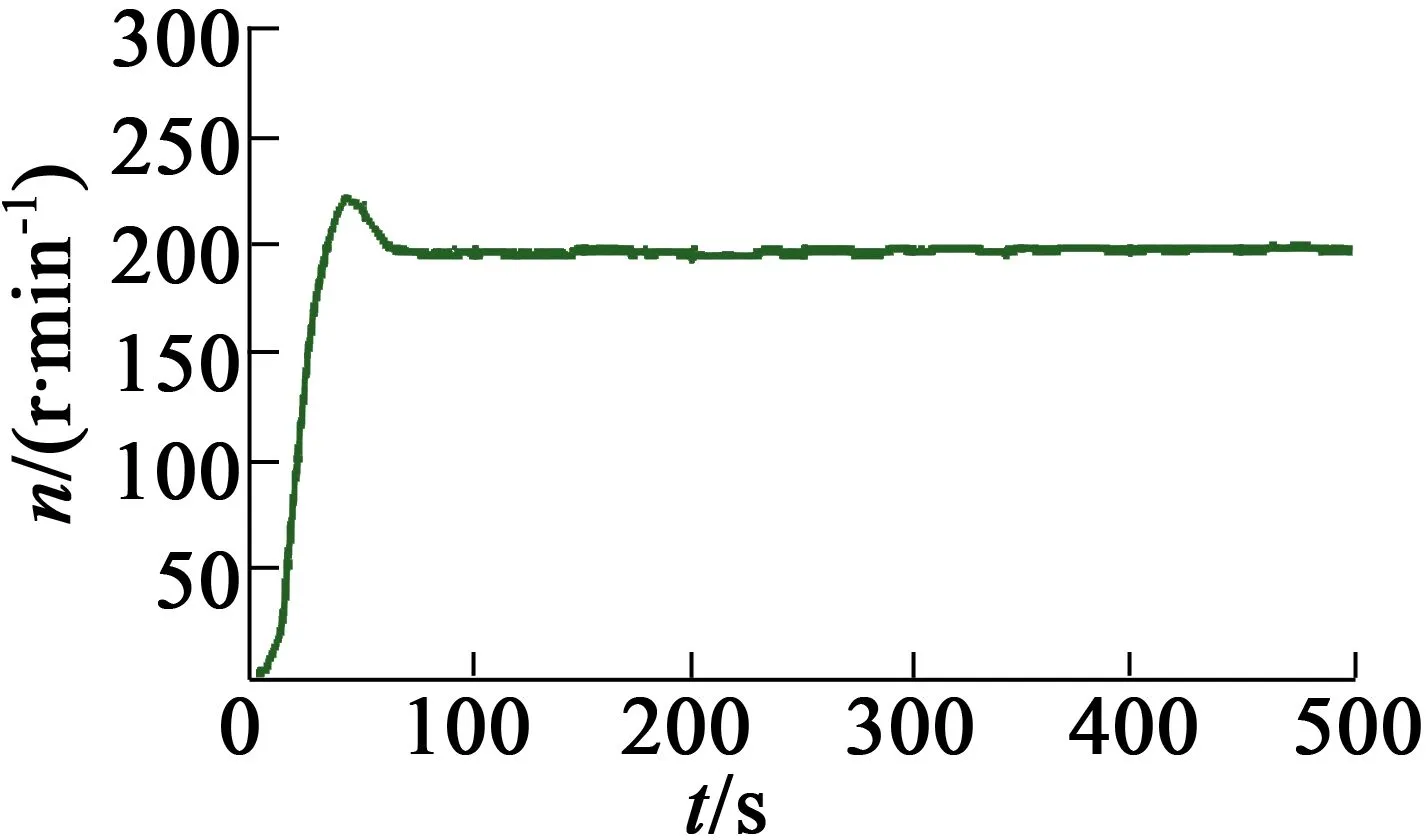
图8 ACPSO-FOPID算法转速响应曲线
图6~图8表明,虽然在外界条件的影响下电机转速有一些波动,并且出现了不同的超调量,但是电机转速曲线和仿真转速曲线的波动性基本一致,证明了仿真结果的正确性,也再次证明ACPSO-FOPID算法性能的优越性。
4 结 语
针对BLDCM的FOPID速度控制器参数难以整定的问题,提出将改进的PSO算法与FOPID相结合,实现5个参数的自适应寻优。由于传统PSO算法存在容易陷入局部最小解、收敛速度慢等缺点,本文通过自适应惯性权重和改进Tent混沌算法局部搜寻两种策略以使算法跳出局部最小解,快速收敛。仿真和样机实验都证明了ACPSO-FOPID算法具有更好的性能指标。这种通过改进的智能算法对新型PID控制器参数寻优的方法具有较强的发展空间及推广价值。
[1] 夏长亮.无刷直流电机控制系统[M].北京:科学出版社,2009.
[2] 文欢,沈怀荣.模糊分数阶控制器在无人机飞行控制中的应用仿真[J].系统仿真技术及其应用,2007,9(7):1333-133.
[3] 梁涛年,陈建军,王媛,等.分数阶系统模糊自适应分数阶PIλDμ控制器[J].北京工业大学学报,2013,39(7):1040-1045.
[4]PODLUBNYI.Fractional-ordersystemsandcontrollers[J].IEEETransactionsonAutomaticControl,1999,44(1):208-214.
[5] 薛定宇,赵春娜,潘峰,等.基于框图的分数阶非线性系统仿真方法及应用[J].系统仿真学报,2006,18(9):2405-2408.
[6]MONJECA,CALDERONAJ,VINAGREBM,etal.Onfractionalcontrollers:sometuningrulesforrobustnesstoplantuncertainties[J].NonlinearDynamics,2004,38(1):369-381.
[7]MONJECA,VINAGREBM,FELIUV,etal.Tuningandauto-tuningoffractionalordercontrollersforindustryapplications[J].ControlEngineeringPractice,2008,16(4):798-812.
[8]BARICM,PETROVICI,PERICN.Neuralnetwork-basedslidingmodecontrolofelectronicthrottle[J].EngineeringApplicationsofArtificialIntelligence,2005,18(8):951-961.
[9] 单梁,强浩.基于Tent映射的混沌优化算法[J].控制与决策,2005,20(2):179-182.
Research on Fractional Order Speed Controller of BLDCM Based on Improved Particle Swarm Optimization Algorithm
JINPeng,LIJing
(Liaoning Engineering Vocational College,Tieling 112008,China)
Fractional order PIλDμcontroller with 5 control parameters, compared with the traditional PID controller, has higher control precision and flexibility. The fractional PIλDμcontroller used in BLDCM control system can improve the performance effectively. However, due to the increase of control parameters, the difficulty of parameter tuning was also improved higher. A method of optimizing the fractional order PIλDμcontroller parameters based on the improved particle swarm optimization algorithm was proposed, and the strategies of adaptive weight and chaotic local search can overcome the problem that the particle swarm algorithm is easy to fall into the minimum local solution and its slow convergence. The feasibility of this method was proved by the simulation and the system's practical operation.
brushless DC motor (BLDCM); fractional order PIλDμ; parameter tuning; particle swarm optimization
2016-01-10
辽宁省教育厅科学研究一般项目(L2012497)
TM33
A
1004-7018(2016)07-0059-04
金鹏(1982-),男,讲师,研究方向为智能控制器。
