换热器的理论强化传热评价准则研究

王斯民,王萌萌,顾昕,简冠平,文键

(1.西安交通大学化学工程与技术学院,710049,西安;2.西安交通大学能源与动力工程学院,710049,西安)



王斯民1,王萌萌1,顾昕1,简冠平1,文键2

(1.西安交通大学化学工程与技术学院,710049,西安;2.西安交通大学能源与动力工程学院,710049,西安)

对于现有的理论只考虑了换热器换热量或传热温差的影响,而没有考虑压降和泵功的问题,分析和推导得出两种新的评价指标ET/EP2/3和ET/EP,并命名为EPEC(entransy performance evaluation criterion)指标,分别表征了单位压降和单位泵功下的换热量,这对换热器传热强化性能评价工作具有重要的参考价值。同时,对18°和27°平面螺旋折流板换热器和折面螺旋折流板换热器的实验结果分别进行了基于热力学第一定律、热力学第二定律以及新的理论评价指标的分析,研究表明:ET/EP2/3和ET/EP与单位压降和单位泵功下的换热量随有效度的变化趋势基本一致,验证了新评价指标的有效性和可靠性。不同评价指标均从不同方面反映了换热器的性能,同时也说明了不同评价指标之间的差异和针对不同换热器不同工况统一标准的必要性。

螺旋折流板换热器;理论;评价准则;可靠性

管壳式螺旋折流板换热器已在我国工业应用冷换设备中占有重要地位,主要有压降小、无滞留死区、不易结垢等优点[1],因此对于螺旋折流板换热器的传热性能强化研究具有重要意义。但是,在实际应用中如何对换热器的传热性能及阻力因素进行综合的评价还是很困难的,且由于换热器种类和型号繁多,至今没有一种评价标准是具有普遍适用性的。

综合评价一台换热器性能包括很多方面,例如换热器的热工性能(传热和阻力)、经济性、运行安全性等,这里只考虑热工性能。常用的换热器热工性能评价指标主要有热力学第一定律的评价方法和热力学第二定律的评价方法[2],基于热力学第一定律的评价方法主要有:换热系数h/h0和阻力因子j/j0的评价方法,随后又以归一化的努赛尔数Nu为标准来进行评价,这些主要针对换热过程的某一量纲进行比较,简单而且直观,但是研究发现,随着换热性能的改善,阻力消耗往往也相应增大,考虑阻力的影响,有学者提出了单位压降下的换热系数K/Δp以及单位阻力因子下的努赛尔数Nu/j等[3]。但是,随着研究的深入,发现有些传热强化技术不能满足单位压降下的换热提高,而在单位泵功情况下可以得到改善,于是从相同消耗功率下传热的大小出发推导出Nu/j1/3作为评价准则[4]。这种综合评价标准目前应用较多。但是,以上指标只考虑了热量传递的数量而没有考虑热量传递的质量。

基于热力学第二定律的评价指标则考虑了热量传递的质量,表征了传热过程的不可逆性,因此也具有重要的意义。Bejan在此基础上提出了以熵产来评价换热器的传热性能[5],换热器的熵产包括由传热和流动过程引起的熵产,但是流动过程比传热过程引起的熵产小很多。也有很多学者采用分析法对换热器进行分析[6],结果也表明了换热器传递的质量。值得注意的是,过增元从热电比拟的角度提出了的概念[7],代表了热量传递的势能,近年来得到广泛应用,但是的极值理论只是考虑了传热过程中的热量或者传热温差,而忽略了压降和泵功的消耗,因此还需要进一步完善。

本文综合了热力学第一定律和热力学第二定律的评价方法,在等压降和等泵功的前提下对关于耗散的换热器评价标准进行了分析,提出了两个新的评价指标,即EPEC(entransy performance evaluation criterion)指标,并对18°和27°平面螺旋折流板换热器和改进的折面螺旋折流板换热器的实验数据分别进行热力学第一定律、热力学第二定律以及新的理论指标评价,从而验证新指标的可靠性。

过增元等基于热电比拟的方法对比发现,在热力学系统中缺乏与电能对应的物理量,从而针对这一点,定义了的概念,用以表征热量的势能[8]

(1)

∫q(x)(Th(x)-Tc(x))dx=T′dq

(2)

式中:C表示热容流量;下标h和c分别表示热流体和冷流体,i和o分别表示进口和出口;q(x)为x处的热流量;Th(x)表示x处的热流体温度;Tc(x)为x处的冷流体温度;T′为换热器壳侧流体温度的平均值。假设换热过程中流体的物性为定值且壳侧温度变化不大,此时传热耗散即和换热量成正比关系,则

Q=nET(n为常数)

(3)

(4)

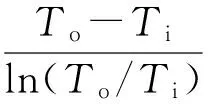
(5)

(6)

式中:m为壳侧流体的质量流量;ρ为流体密度;Δp为壳侧压降。总耗散为二者之和

E=ET+EP

(7)

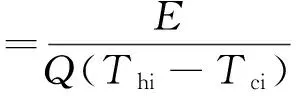
(8)

式中:E*被称为总耗散数;Q为实际换热量。

由文献[12]可知,因流动阻力引起的熵产远远小于传热温差熵产,因此本文忽略流动引起的熵产,仅考虑传热引起的熵产

(9)

一般来说,换热量或换热系数增加的同时,阻力也相应增加,所以为了在相同阻力情况下得到更大的换热量,采用单位压降下的换热量Q/Δp来进行评价,对应于理论时,由上文可知,传热耗散与换热量成正比关系。对于压降

(10)

(11)

(12)

式中:u为壳层最小流通截面的流速;L为换热管的长度;ρs为导热油密度;ν为导热油运动黏度;qv为壳侧热传导油流量;do为换热管外径;Sz为最小流通截面积。

管外横向冲刷管子湍流流动的阻力系数关联式为[13]

f=cRe-0.25

(13)

则阻力系数f与Re-0.25成正比,即f～Re-0.25,所以当介质物性不变且螺旋折流板换热器的结构给定时

Δp=au2Re-0.25=bRe1.75

(14)

即Δp和Re1.75成正比

(15)

EP和Re2.75成正比。

(16)

以上式中a、b、c、c0、d均为常数,且由上文推导可知,Q～ET

(17)

经研究和实践验证,有时单位压降下的换热量并不能很好地表示换热量和阻力之间的关系,而单位泵功下的换热量却得到改善,因此有学者提出采用Q/W来表示消耗相同的泵功时换热量的大小,而在理论上,由上文可知,传热耗散和换热量成正比关系ET～Q,且由上文

(18)

螺旋折流板换热器的泵功为

W=SzuΔp

(19)

对于螺旋折流板换热器

Sz=0.5B(D-Ndo)

(20)

式中:B为螺旋折流板换热器螺距;D为壳体内径;N为换热管排数。

在壳侧内径、换热管外径和螺距不变的情况下,螺旋折流板换热器的最小流通面积即保持不变,则此时换热器的阻力耗散正比于换热器泵耗功率

EP=kW

(21)

(22)

因此,ET/EP表示了单位泵功下的换热量大小。

2 螺旋折流板结构的改进

目前,螺旋折流板常用的板式均为1/4圆的扇形折流板结构,一个螺距由4块折流板前后搭接组成,此时壳侧大部分流体沿着折流板和管束组成的近似螺旋通道流动,但同时也有一部分流体沿着相邻两折流板之间的搭接三角区形成的快速流道流动,形成螺距为4倍管束螺距的另一股螺旋漏流,偏离了理想的螺旋流,影响了螺旋折流板换热器的换热性能。因此,王斯民等提出了折面螺旋折流板的结构[15],由图1中可以看出,折面折流板使相邻两块平面折流板在搭接时所形成的夹角合拢,即漏流三角区被有效封闭,从而改善了传统螺旋折流板换热器在搭接处的漏流,使壳程的流动更加接近于标准的螺旋流,靠近管束中心区域的流体的流速也相应增大,流体与换热管的接触更加充分,故强化了传热。

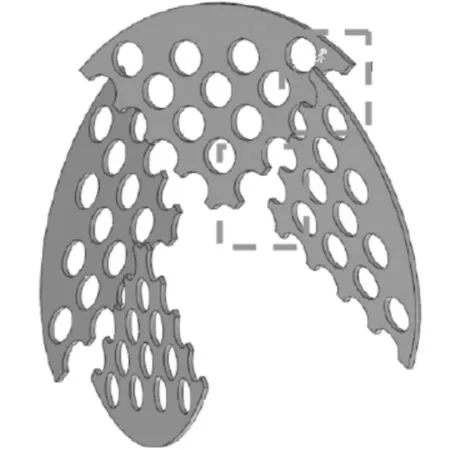
(a)平面螺旋折流板

(b)折面螺旋折流板图1 螺旋折流板结构示意图

3 实验流程与方法

实验主要针对50%搭接度,螺旋角分别为18°、27°的平面螺旋折流板与折面螺旋折流板共4种结构,壳体内径为250 mm、长2 000 mm。在其他结构参数和操作工况不变的条件下,研究不同板型结构下的螺旋折流板换热器的传热和阻力性能。

实验流程布置如图2所示,实验系统主要由壳侧的油路循环和管侧的水路循环以及测试系统组成。冷却水从水箱开始,经换热器加热后送到冷却塔进行冷却,循环用的水贮存于水箱中,通过水泵进入系统循环使用。壳程采用昆仑L-QC310导热油,导热油从膨胀槽开始,通过电加热器加热到所需的温度后经油泵进入换热器。保持管程和壳程流体进口温度和管程流量基本不变,改变壳侧导热油的流量进行分组实验。

实验数据采集系统采用多通道数据采集仪,实时监控测量数据及变化。实验中采集的数据包括管程水和壳程导热油的进出口温度、流量以及进出口的压差。管侧水的体积流量使用LWGY系列涡轮流量计测量,壳侧导热油流量采用耐高温的DLWGY系列涡轮流量计测量,误差均为0.5%。温度采用热电阻进行测量,误差小于0.2%。进出口的压差则采用压差变送器测量,误差为0.5%。以上数据的测量均在每组工况改变一段时间以后,即流动较为稳定以后测得[16]。

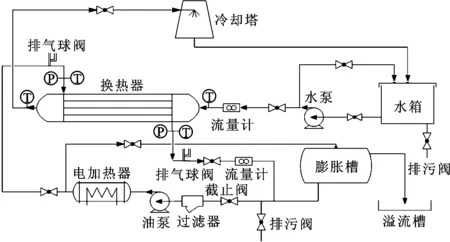
图2 换热器性能实验流程图

4 螺旋折流板换热器的实验结果分析

4.1 基于热力学第一定律的性能评价

图3为不同板型结构下螺旋折流板换热器的总换热系数K随壳侧流量的变化曲线。从图中可以看出,不同结构下总换热系数均随着壳侧流量的增大而增大,且在流量相同时,折面螺旋折流板换热器的总换热系数大于平面螺旋折流板换热器。螺旋折流板板型相同时,18°螺旋角的螺旋折流板换热器换热系数均大于27°螺旋角的。这是由于折面螺旋折流板有效封堵了搭接三角区的快速流道,使流体向壳体中心聚拢,流体与换热管表面进行了更充分的接触和换热。在板型结构相同、但螺旋角更小时,相同壳体长度下的螺距更小,螺旋周期数增加即螺旋折流板的数目增多,且相同的壳侧流量下,螺旋角更小时壳侧流速更大,因此换热得到强化[17]。

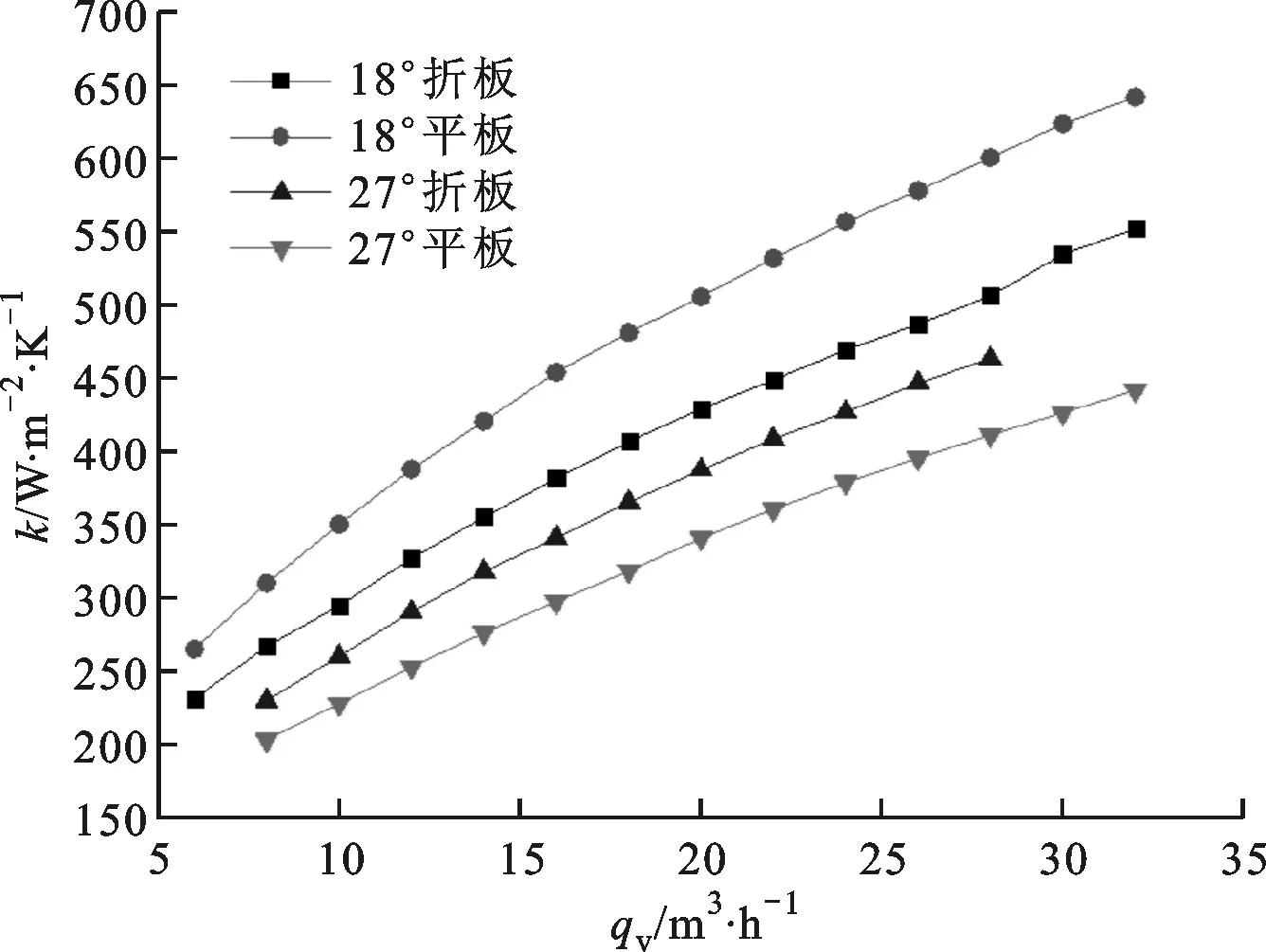
图3 总传热系数随壳侧流量的变化曲线

图4显示了螺旋折流板换热器的总压降随壳侧流量的变化趋势。由图中可知,总压降均随着壳侧流量的增大而增大,且在流量不变的情况下,折面螺旋折流板换热器的压降均大于平面螺旋折流板换热器。板型结构相同时,18°螺旋折流板换热器的压降大于27°螺旋折流板换热器。这是因为折面螺旋折流板使得原先流过4倍螺距的快速通道的流体沿着单倍螺距的螺旋流道流动,流体流经的管子数目增加,同时流体的轴向速度减小,流体流动更接近于横向流,增加了流动的阻力。壳体总长不变时,18°螺旋角的螺旋折流板数目大于27°螺旋角的,因此壳侧流体流经折流板时碰撞次数更多,导致了阻力的增加。

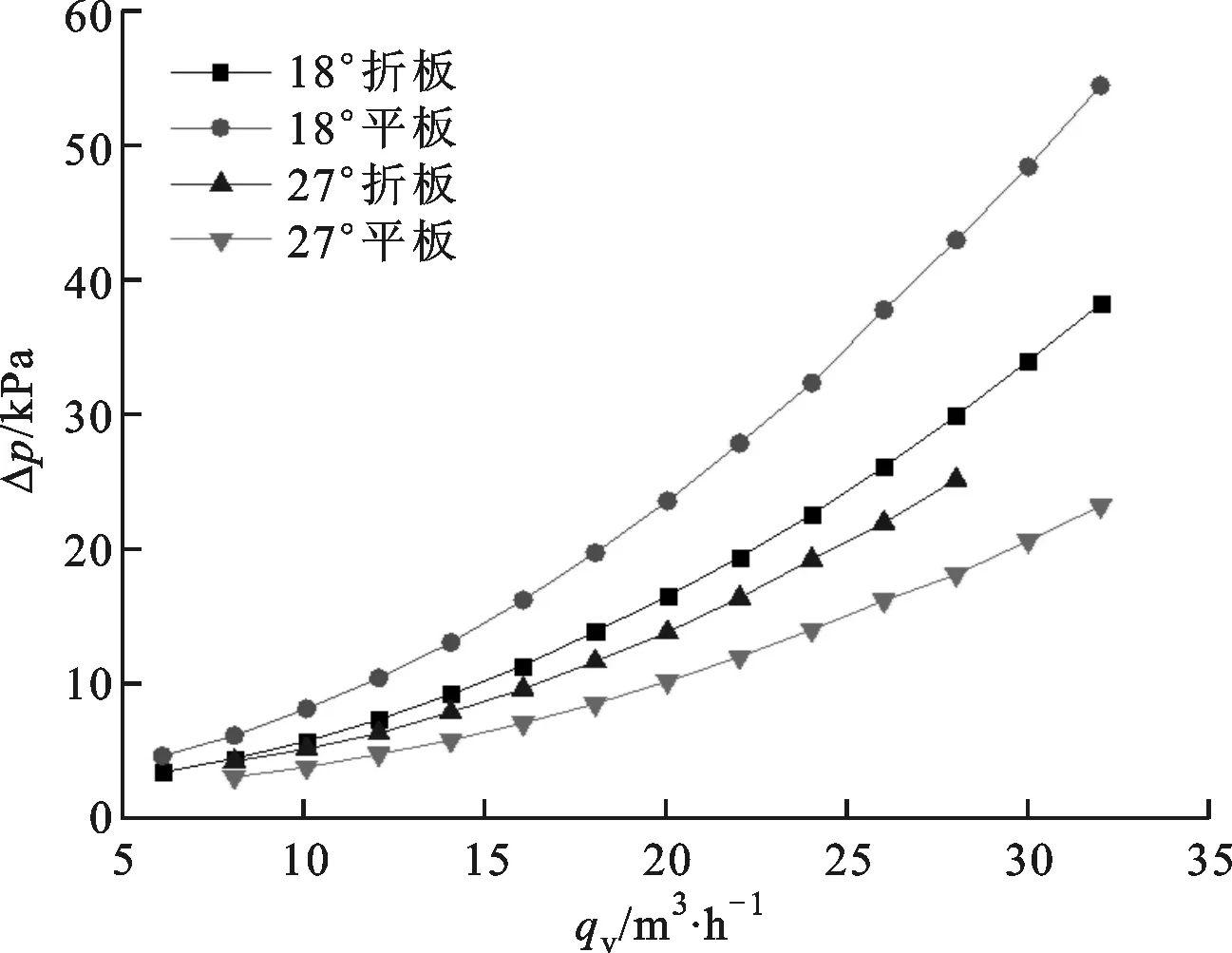
图4 总压降随壳侧流量的变化曲线

图5表明了换热器常用的综合评价指标PEC准则数Nu/f1/3随壳侧导热油流量变化的趋势。从图中可以看出,在流量、螺旋角、搭接度均相同的情况下,折面螺旋折流板换热器的综合性能均优于平面螺旋折流板换热器,说明折面螺旋折流板换热器阻止了三角漏流,有效地提高了换热器的性能。在流量相同的情况下,18°、50%搭接度的折面螺旋折流板换热器的性能最佳,且明显优于27°螺旋角的情况。这是由于在螺旋角较小时,换热器内螺旋周期数较多,流道变窄而流体流过的路径更长,流体在换热器中的湍动也会更加强烈,所以小螺旋角时的综合评价性能更高。

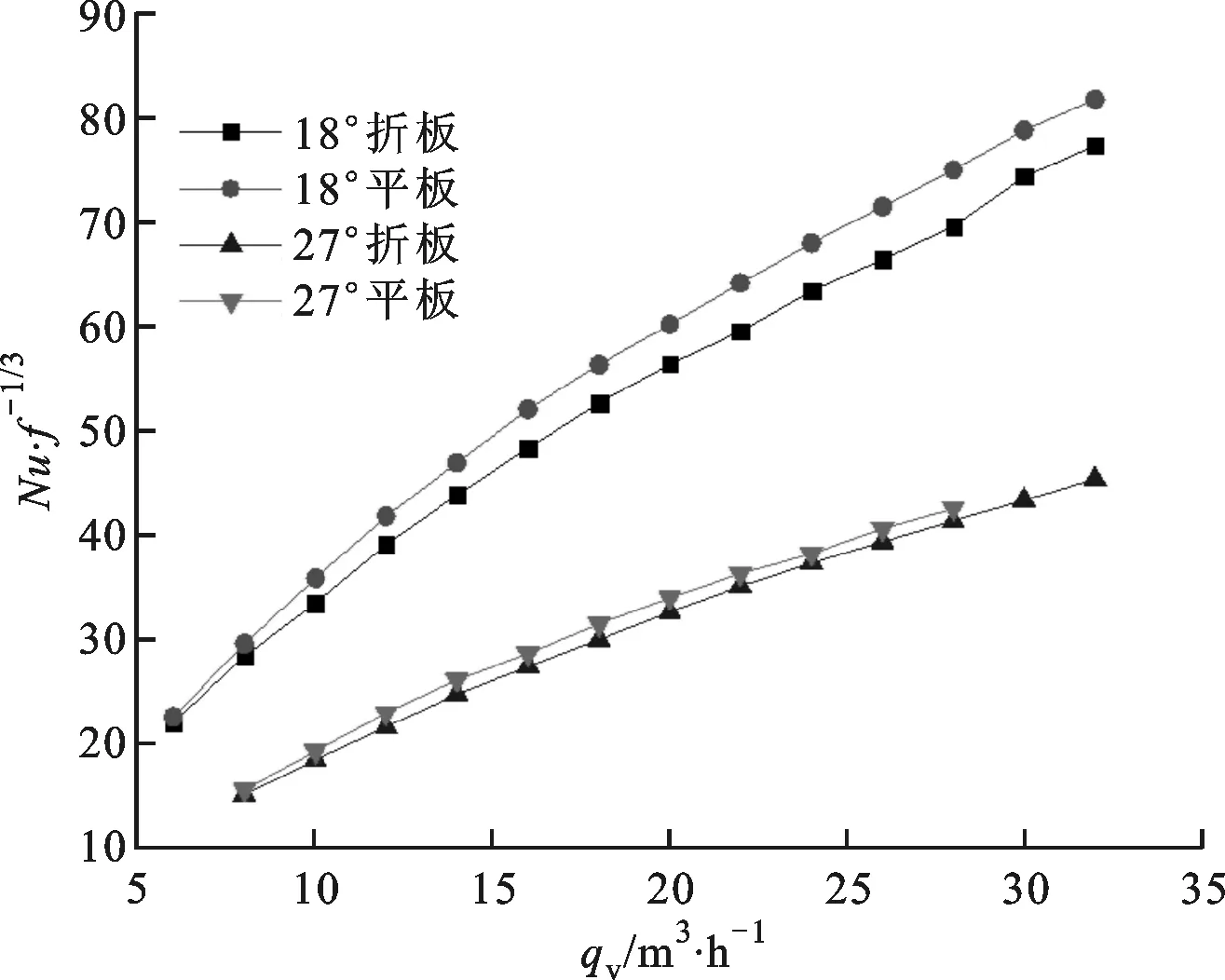
图5 Nu/f1/3随壳侧流量的变化曲线

4.2 基于热力学第二定律的性能评价

本文只考虑了壳侧传热引起的熵产S,由于螺旋折流板实验中壳侧导热油温度降低,因此得到的壳侧熵产为负值。由图6可知,随着有效度的增加,壳侧熵产均随之增大,即有效度越大,换热过程的不可逆性越大。在相同有效度的情况下,18°平面螺旋折流板换热器的熵产最小,即传热过程的不可逆损失最小,性能最优。由图6还可知,当螺旋角相同时,折面螺旋折流板换热器的不可逆损失均小于平面螺旋折流板换热器,表明折板有效地改善了螺旋折流板换热器的壳侧流动,增强了换热。

图6 壳侧熵产随有效度的变化曲线

图7 总耗散数随有效度的变化曲线

图8 单位压降下的换热量随有效度的变化曲线

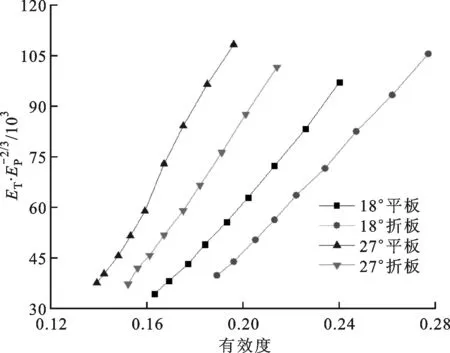
图随有效度的变化曲线

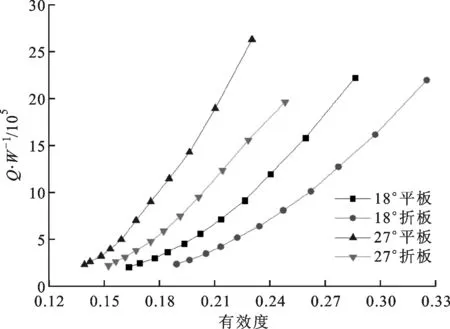
图10 单位泵功下的换热量随有效度的变化曲线

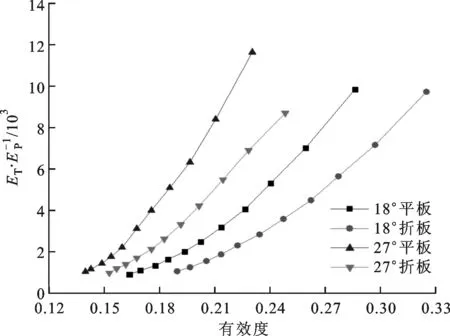
图11 ET/EP随有效度的变化曲线

图10和图11给出了单位泵功下的换热量Q/W、ET/EP与有效度之间的关系,由图中可知,单位泵功下的换热量和ET/EP随有效度的变化趋势基本一致,验证了ET/EP的物理意义的正确性。从图中还可知,随着有效度的增加,单位泵功下的换热量和ET/EP均随之增大,即随着流量的增大,泵功增加的比例大于换热量增加的比例,则单位泵功下的换热量和ET/EP相应减小,在有效度相同的条件下,27°平面螺旋折流板换热器在单位泵功下的换热量最大,且在螺旋角相同时,平面螺旋折流板换热器单位泵功下的换热量均大于折面螺旋折流板换热器,这说明折面螺旋折流板换热器在改善壳侧流动换热的同时也引起了更大的泵耗功。

综合以上基于热力学第一定律和热力学第二定律的评价指标分析,对于单个的换热系数和压降等的分析均只考虑了一方面的影响因素。换热器换热性能增加的同时往往伴随着压降或泵功的消耗,因此综合考虑各种因素更为合理,但同时考虑到换热量、压降、泵功之间增量的数量级之间的差异,且有时压降和泵功在工业允许范围内侧重于追求换热性能的提高等因素,故不同情况下仍需考虑合适的评价标准。每一种评价指标可能都从不同角度反映了换热器的性能,但是针对不同的换热器类型如何采取统一的评价指标还需要进一步完善。本文的EPEC准则是对理论评价标准的完善,综合考虑了换热性能和损耗之间的关系,对于理论的进一步发展具有重要意义。

5 结 论

(1)本文考虑了压降和泵功的因素,首次经过分析和推导得出两种新的基于传热耗散和阻力耗散之间的评价指标和ET/EP,分别表征了单位压降和单位泵功下的换热量的评价指标,这对换热强化的评价工作具有重要意义。

(2)由热力学第一和第二定律评价指标分析可知,18°平面螺旋折流板换热器的综合性能最优,且在螺旋角相同的情况下,折面螺旋折流板换热器的性能优于平面螺旋折流板换热器,证明折面螺旋折流板换热器有效地阻挡了壳侧三角漏流区,使壳侧流场更加接近于螺旋流,增强了换热。

(4)不同的评价指标分析结果均有不同的侧重,说明了不同评价指标之间的差异和针对不同换热器不同工况统一标准的必要性,应用过程中要结合实际需要进行选择。

[1] 文键, 杨辉著, 杜冬冬. 螺旋折流板换热器换热强化的数值研究 [J]. 西安交通大学学报, 2014, 48(9): 43-48. WEN Jian, YANG Huizhu, DU Dongdong. The numerical studies on the heat transfer reinforcement of the helical baffle heat exchanger [J]. Journal of Xi’an Jiaotong University, 2014, 48(9): 43-48.

[2] 何雅玲, 陶文铨, 王煜, 等. 换热设备综合评价指标的研究进展 [C]∥中国工程热物理学会学术会议论文. 北京: 中国工程热物理学会, 2011: 113599.

[3] 过增元, 程新广, 夏再忠. 最小热量传递势容耗散原理在导热优化中的应用 [J]. 科学通报, 2003, 48: 21-25. GUO Zengyuan, CHENG Xinguang, XIA Zaizhong. The application of the principle of minimum heat transfer potential capacity dissipation in the optimization of thermal conductivity [J]. Chinese Science Bulletin, 2003, 48: 21-25.

[4] 韩光泽, 过增元. 导热能力损耗的机理及数学表述 [J]. 中国电机工程学报, 2007, 27(17): 98-102. HAN Guangze, GUO Zengyuan. Thermal capacity loss mechanism and mathematical expression [J]. Proceedings of the CSEE, 2007, 27(17): 98-102.

[5] BEJAN A. Entropy generation through heat and fluid flow [M]. New York, USA: Wiley, 1982.

[7] 过增元. 热学中的新物理量 [J]. 工程热物理学报, 2008, 29(1): 112-114. GUO Zengyuan. The new thermal physical quantities [J]. Journal of Engineering Thermal Physics, 2008, 29(1): 112-114.

[8] GUO Jiangfeng, XU Mingtian, CHENG Lin. Principle of equipartition of entransy dissipation for heat exchanger design [J]. Science China Technological Sciences, 2010, 53: 1309-1314.

[9] 过增元, 李志信, 周森泉, 等. 换热器中的温差场均匀性原则 [J]. 中国科学: E辑 技术科学, 1996, 26: 25-31. GUO Zengyuan, LI Jiaoxin, ZHOU Senquan, et al. The principle of uniformity of the temperature difference of heat exchanger [J]. China’s Scientific: E Science and Technology, 1996, 26: 25-31.

[10]GUO J F, CHENG L, XU M T. Entransy dissipation number and its application to heat exchanger performance evaluation [J]. Chinese Sci Bull, 2009, 54(15): 2708-2713.

[11]郭春生, 程林, 杜文静. 换热器新评价标准:耗散均匀性系数 [J]. 哈尔滨工业大学学报, 2012, 44(3): 144-148. GUO Chunsheng, CHENG Lin, DU Wenjing. New heat exchanger evaluation standard: entransy dissipative uniformity coefficient [J]. Journal of Harbin Institute of Technology University, 2012, 44(3): 144-148.

[12]杨辉著, 文键, 王斯民. 螺旋折流板换热器的熵产分析 [J]. 化学工程, 2014, 42(11): 45-50. YANG Huizhu, WEN Jian, WANG Simin. Entropy analysis of the helical baffle heat exchanger [J]. Chemical Engineering, 2014, 42(11): 45-50.

[13]SANO Y, USUI H. Evaluation of heat transfer promoters by the fluid dissipation energy [J]. Heat Transfer-Japanese Research, 1982, 11(1): 91-96.

[14]徐国想, 邓先和, 许兴友, 等. 换热器传热强化性能评价方法分析 [J]. 淮海工学院学报, 2005, 14(2): 42-44. XU Guoxiang, DENG Xianhe, XU Xingyou, et al. The analysis of evaluation method on heat exchanger heat transfer enhanced performance [J]. Journal of Huaihai Institute of Technology, 2005, 14(2): 42-44.

[15]王斯民, 文键. 无短路区新型螺旋折流板换热器换热性能的实验研究 [J]. 西安交通大学学报, 2012, 46(9): 12-15. WANG Simin, WEN Jian. Experiment on heat transfer performance of helical baffled heat exchanger without short circuit flow [J]. Journal of Xi’an Jiaotong

University, 2012, 46(9): 12-15.

[16]王斯民, 明玉生, 陈亢, 等. 螺旋折流板换热器三角区漏流阻塞的实验研究 [J]. 化工学报, 2014, 65(9): 3389-3394. WANG Simin, MING Yusheng, CHEN Kang, et al. The experimental research on the triangle leakage flow jam of the helical baffle heat exchanger [J]. Chemical Engineering, 2014, 65(9): 3389-3394.

[17]曹春暖. 高效螺旋折面板换热器数值模拟研究 [D]. 西安: 西安交通大学, 2013.

[18]ANDRESEN B, GORDON J M. Optimal paths for minimizing entropy generation in a common class of finite time heating and cooling processes [J]. International Journal of Heat and Fluid Flow, 1992, 13: 294-299.

(编辑 荆树蓉)

Research on the Heat Transfer Enhancement Evaluation Criterion of Heat Exchanger Based on Entransy Theory

WANG Simin1,WANG Mengmeng1,GU Xin1,JIAN Guanping1,WEN Jian2

(1. School of Chemical Engineering and Technology, Xi’an Jiaotong University, Xi’an 710049, China;2. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

In consideration of the fact that present entransy theory only paid attention to the influence of heat exchange amount or heat transfer temperature difference, without taking into account the pressure drop and pump power, we analyzed and derived two entransy evaluation criteria EPEC (entransy performance evaluation criterion) related to heat transfer entransy dissipation and resistance entransy dissipation, which represent the heat transfer capacities under unit pressure drop and pump power, respectively. These two evaluation criteria have important reference value to the performance evaluation of enhanced heat transfer. In addition, this paper also analyzed the experimental results of the 18° and 27° plane helical baffle heat exchanger and folding helical baffle heat exchanger based on the first and second laws of thermodynamics and the new entransy evaluation indicators. The results show that the changing tendencies ofET/EP2/3andET/EPwith the effective degree are in good agreement with that of the heat transfer under unit pressure drop and pump power, verifying the validity and reliability of the new evaluation indicators. Different evaluation indicators reflect the performance of heat exchanger in different ways, which also illustrate the difference between different evaluation criteria and the necessity to unify the evaluation criteria for different heat exchangers under various working conditions.

helical baffle heat exchanger; entransy theory; evaluation criterion; reliability

2015-04-22。 作者简介:王斯民(1977—),男,副教授。 基金项目:国家自然科学基金资助项目(51106119,81100707);教育部高等学校博士学科点专项科研基金资助项目(20110201120052);中央高校基本科研业务费专项基金资助项目。

时间:2015-10-13

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151013.1133.006.html

10.7652/xjtuxb201601001

TK464

A

0253-987X(2016)01-0001-07