互联网远程实时控制系统短时间窗口往返时延测量、分析与建模

于赫,秦贵和,2,孙铭会,2,李滨,吴星辰

(1.吉林大学计算机科学与技术学院, 130022, 长春;2.吉林大学符号计算与知识工程教育部重点实验室, 130022, 长春)



互联网远程实时控制系统短时间窗口往返时延测量、分析与建模

于赫1,秦贵和1,2,孙铭会1,2,李滨1,吴星辰1

(1.吉林大学计算机科学与技术学院, 130022, 长春;2.吉林大学符号计算与知识工程教育部重点实验室, 130022, 长春)

为了得到准确地描述互联网远程实时控制系统时延的分布模型,对短时间窗口往返时延(round-trip time, RTT)进行了测量、统计和分析,提出了一种短时窗RTT时延混合威布尔(Weibull)模型。该混合模型满足网络控制系统的实时性需求,具备对短期非平稳的短时间窗口RTT时延样本随机聚类特性的描述能力,并利用期望最大化(expectation-maximization, EM)算法估计模型的混合分量密度及混合分量模型参数。实验结果表明:使用二重混合威布尔模型建模短时窗RTT时延样本能够很好地反映时延的随机聚类特性,K-S检验显示该模型对样本匹配效果评价可接受,该模型为互联网远程控制系统的优化控制提供了一种更准确的参考模型。

RTT时延;网络控制系统;混合威布尔模型;期望最大化算法

以互联网为基础设施和实现工具,将互联网与传统产业相结合是新一代信息技术与创新的发展方向。近年来,网络接入的速度和移动终端的计算性能都成几何级数增长,通过互联网进行的远程实时控制应用焕发出新的活力。然而,Internet的复杂性远超经典NCS使用的现场总线、工业以太网等网络系统,当控制系统以互联网为基础设施时,网络时延对控制系统设计、优化的影响是不可忽视的。

往返时延(round-trip time, RTT)是描述网络性能的一项关键指标,有效的RTT时延分析可实现互联网实时系统的优化控制。目前互联网时延相关研究成果多集中于对网络性能的提升,Ciucu等基于网络演算理论对端到端时延界限进行分析,使用统计服务曲线确定时延界限,从而得到更好的网络资源利用率[1-2];通过大量网络测量数据,时延空间模型针对大规模网络在网络坐标系统的基础上建立时延空间模型,寻找互联网时延空间的等距同构空间,例如云计算等服务请求寻求更小的服务时延,从而提高服务质量[3-5];在宏观现实网络拓扑、长时间跨度和大量测量数据的基础上,对互联网时延的特性等相关问题进行探讨[6-8]。通过互联网进行的远程实时控制系统的控制数据传输具有单一数据包数据量小、控制数据包发送频率高等特点,与大规模网络测量分析相比,互联网实时控制系统更关注短时间窗口内的高频数据包RTT时延的特性。

本文针对基于互联网的远程控制系统应用场景,编写专用测试工具,采集短时间高频RTT时延样本。在此基础上,通过统计分析方法对时延样本的特性进行剖析,提出使用混合模型建模互联网实时控制系统RTT时延,最后对进一步的研究工作进行了探讨。

1 时延样本采集

1.1 时延样本采集工具

目前网络测量广泛使用的数据样本提供组织及公司有CAIDA、RIPE Atlas、PingER、AMS-IX等,这些组织及公司提供或开源分享的网络测量样本绝大多数为研究网络性能、框架和大规模网络分析使用,样本数据中很难找到符合基于互联网的实时系统的时延样本。网络化实时系统的控制数据包携带的数据域长度短、发送周期快,因此本文针对网络化实时系统的时延测量需求进行了优化,自主开发了网络时延测量样本采集工具。

时延样本采集工具系统平台为Windows 7,测试端程序在Microsoft Visual 2010环境下由C++语言开发实现,通过WinPcap开源库,越过操作系统直接调用网络硬件接口,对测试报文进行封装、发送和收集,这与实际的网络化控制系统不依赖特定操作系统的工作模式相近。

测试工具使用ICMP协议中Echo/Reply报文类型实现对远程目的节点的RTT时延探测,用户设置远程目的节点IP、采集数量、数据包发送间隔和携带的数据长度后,生成原始数据报文,调用网卡一发送至网络;同时启用网卡二对本地网络中的报文进行捕获,自定义过滤除源地址为探测目标IP,目的地址为本机的ICMP Reply响应报文,对接收的报文进行处理,计算响应时间,返回给采集工具客户端显示并写入文件存储,程序流程如图1所示。

图1 RTT时延采集工具流程图

本文自主设计的采集工具根据需求发送不同长度测量数据包,发送间隔可达到毫秒级,网络RTT时延获取精度在微秒级,符合进行下一步统计分析的需求。

1.2 采集时延样本

使用自主设计的时延采集工具,进行时延样本采集。每次样本采集持续时间为15 min,发送周期为250 ms,携带数据域为48个字节,默认的超时时间是1 500 ms,每次可获得一个包含3 600个RTT时延的样本。由于本文专注于短时间窗口RTT时延的研究分析,因此没有进行长时间连续性的RTT时延采集。

图2a是IP为182.254.8.146的A线路在09:30时采集的时延样本截取,图上显示线路A在晨间时段的时延较小,仅在正负10 ms区间内变化。图2b为截取的线路A中第160～240个RTT时延样本的独立显示,参考250 ms的采集周期,不难发现在约20 s左右的时间内线路A的RTT时延出现了一次短暂的小幅度跃升,这种短时的变化很难在大规模长时间的网络测试统计分析中被注意到,而这种变化在网络化实时控制系统中往往是不可忽视的。

(a)A线路时延样本

(b)A线路第160至240个时延样本图2 RTT时延样本

2 时延统计分析

2.1 数据预处理

在数据分析中,异常点对分析结果的影响不可预知,因此在进行RTT时延统计分析之前首先要剔除采集样本中的异常点。实际网络中,丢包现象是无法避免的,使用ICMP协议并不会保证数据包可达,测试工具中的默认超时时间为1 500 ms,一旦超时将会返回Time out。在预处理中本文直接将这些点作为异常点删除。

2.2 短期平稳性分析

如果一个随机过程能够满足平稳条件,对其特性分析将会极大简化。因此,分析的第一步是检验数据是否符合平稳条件。

如果一个随机过程满足下列条件:①随机过程的期望E[xt]为常数,即mx(t)=mx;②自相关函数Rx(t1,t2)=Rx(τ),τ=t1-t2,即自相关函数值依赖于时间差,而与绝对时间t无关,可称该随机过程是广义平稳随机过程。

判断一个随机过程是否平稳的方法有参数检验和非参数检验方法两大类。对于参数检验,往往需要一定的模型假设,对于RTT时延这类完全数据驱动的过程,在进行平稳性检验时考虑使用非参数检验。

样本自相关函数(ACF)为

rτ=cτ/c0

(1)

,

τ=0,1,…,K

(2)

(3)

式中:c0是样本{xK}的方差。

图3给出采集RTT时延某一样本序列的自相关函数,图3a、图3b分别使用完整的样本序列计算得到。图3a阶数为100,图3b阶数为250,图中平行线之间为95%的置信区间。通常情况下,一个随机过程如果是平稳的,则样本的ACF有截尾或拖尾特征,拖尾呈复指数衰减或呈振荡式衰减。对于同一个整体样本,图3a在阶数为100时,ACF衰减缓慢。图3b阶数为250时,呈现线性下降趋势,这表明该过程不满足均值平稳过程。图3c、图3d分别是从两个完整样本中抽取连续60个采集时延数据的ACF,图3e、图3f分别为从上面两个完整样本中抽取200个连续时延数据的ACF。图3c、图3d、图3e中,在K>3时,ACF均落入95%的置信区间内,且逐渐趋于0,可认为该过程具有平稳性,而在图3f中,同一组数据取不同阶数时,在K=28时其ACF落入置信区间之外。

(a) 完整样本, (b) 完整样本, (c) 60个样本点,阶数为100 阶数为250 阶数为20

(d) 60个样本点, (e) 200个样本点, (f) 200个样本点,阶数为20 阶数为20 阶数为30图3 短时间窗口RTT时延自相关性

由此可见,通过ACF进行短期平稳性分析高度依赖于经验,由此,本文不支持短时窗RTT时延具有平稳性的假设。

2.3 游程检验

鉴于短时窗RTT时延不具备平稳性,本文考虑对RTT时延样本的随机性进行初步分析,以期望对模型选择提供参考。游程检验是一种非参数统计分析方法,一般对离散型随机变量随机性进行检验。二元序列中,“+”和“-”交替出现,由“+”或“-”连续构成的串为一个游程,序列中游程的个数用R表示。如果一个序列的R较大,证明“+”、“-”交替特征明显,R较小说明“+”、“-”分布相对集中,这两种情况都不符合随机性要求。可以借助R来设定假设检验的拒绝域。R的分布特征和拒绝域证明不是本文重点,可参考文献[9]。

设X=(x1,x2,…,xT)是一段长度为T的RTT时延采集样本,其中T=mn。针对样本X游程检验的步骤如下。

步骤1 样本X分为m个长度为n的时延子样本Yj,其中j=1,2,…,m。

步骤2 对每个子样本Yj求均值,zj=mean(Yj),

其中j=1,2,…,m。

步骤3 对序列Z=(z1,z2,…,zm),计算中值

mean(Z)。

步骤4 对序列Z=(z1,z2,…,zm),规定

(4)

(5)

对序列Z=(z1,z2,…,zm)进行游程检验。假设

(6)

设定显著性水平α=0.05。h=1返回,表示拒绝零假设,即认为序列的出现不是随机的,相反则接受零假设,认为序列的出现是随机的。

图4为一组m=15、n=30时延样本箱图,图上可以直观反映样本“+”和“-”交替情形。

对采样的RTT时延进行抽取,并选择不同的m、n取值进行检验,结果见表1。检验的结果显示短时间窗口的RTT时延的出现并不随机,游程数少且P值较小,具有明显的聚类倾向,因此本文选择使用混合模型建模短时间窗口的RTT时延。

3 混合模型

3.1 威布尔分布

两参数威布尔分布的概率密度函数可表示为

f(x;α,β)=p(x|α,β)=

(β/α)(x/α)β-1exp[-(x/α)β],x≥0

(7)

式中:α,β>0,α为尺度参数,β称为形状参数。

图4 RTT时延样本箱图(m=15,n=30)

如图5所示,分别固定α和β,易见参数α控制模型的定位,而β对尾部行为影响较大。当β=1时,威布尔分布变形为指数分布,指数分布可以看作威布尔分布的一种特殊形式,指数分布已被广泛用于表示独立随机事件发生的时间间隔分布,如网络服务到达曲线等;并且威布尔分布可以方便地近似表示其他典型概率分布,具有良好的适用性。因此本文选择使用混合威布尔模型来表征短时RTT时延特性。

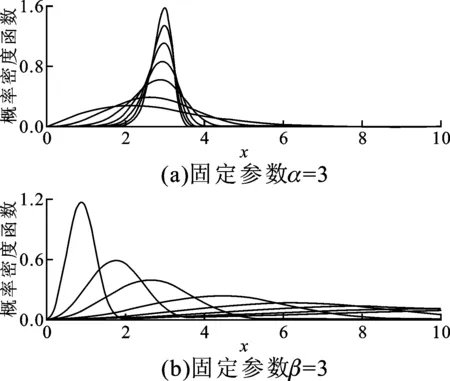
图5 两参数Weibull分布密度函数

3.2 混合威布尔模型

定义有限威布尔混合模型是指具有如下形式的概率分布模型[10-12]

(8)

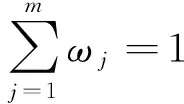
设X=(x1,x2,…,xn)为一组n个RTT时延数据的观测样本,可由m重混合威布尔分布得出。定义隐变量Z,p(zi=j|xi,Θ)表示观测样本xi属于第j个子部的概率,其中i=1,…,n,j=1,…,m。

完全数据的对数似然函数为

(9)

对于含有隐变量Z的概率模型参数的极大似然估计,可使用EM算法估计混合模型参数。

3.3 混合模型参数估计

EM算法的迭代由E步(求期望)和M步(极大化)两步组成。

E步Q(Θ,Θ(k))=E[logp(X,Z|Θ)|X,Θ(k)]

(1)E步 记Θ(k)为第k次迭代参数Θ的估计值,在第k+1次迭代的E步,计算

(10)

式中:p(zi=j|xi,Θ(k))是在给定观测数据X和参数估计Θ(k)下隐变量Z的条件概率分布,由贝叶斯公式和全概率公式不难得到

(11)

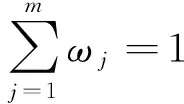
(12)

式(12)对ωj求偏导等于0,得到

(13)

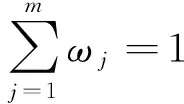
(14)

(15)

(16)

同理可得

(17)

重复以上计算,不断更新式(14)、式(16)、式(17)直到对数似然函数值不再有明显变化为止。

3.4 混合模型验证

考虑到嵌入式实时系统终端的计算能力,选择使用二重混合威布尔模型。图6为一组短时间窗口RTT时延使用二重混合威布尔分布模型匹配结果,可见直方图与密度分布曲线的拟合效果较好,Q-Q图显示基本落在直线及附近,直观上可认为二重混合威布尔分布模型可以很好地表征短时间窗口的RTT时延。

除此之外,仍然需要更有效的证据表明其匹配结果,普遍的做法是使用统计假设检验方法,如χ2检验验证模型的有效性,但是由于短时间窗口RTT时延样本数和最大频数都不能达到χ2检验的基本要求,因此,在验证模型有效性时,本文使用Kolmogorov-Smirnov检验法(K-S检验)。

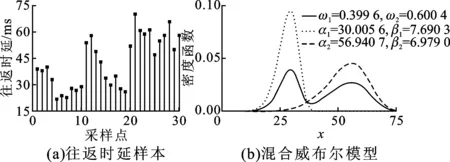
图6 二重混合威布尔分布模型匹配RTT时延

K-S检验是一种非参、高鲁棒性的检验方法,不依赖于均值的位置并且对理论分布函数形式不敏感。K-S检验统计量定义为随机样本的经验分布函数和理论分布函数间的最大偏差Dn,假设

(18)

(19)

(20)

式中:K=sup|B(t)|,其中B(t)为布朗桥过程;Fn(x)为样本经验分布函数;F(x)为理论模型分布函数。K-S检验统计量在n趋于无穷时收敛到max(B(F(t)),即可近似认为当H0为真时,K-S检验统计量依分布收敛于Kolmogorov分布。

表2为某一样本不同短时间窗口RTT时延样本使用二重混合威布尔模型匹配的参数及K-S检验结果。该样本测试周期为250 ms,样本长度为1 500。表2前4项K-S检验结果显示二重混合威布尔模型可以用来表征短时间窗口RTT时延。在表中最后一行对完整样本也使用了二重混合威布尔模型匹配,结果显示二重模型并不能很好地表征长时间RTT时延分布特性。在长时间、粗粒度RTT时延分布特性问题上,有研究者使用五重混合模型得到了较好的匹配结果[13]。

4 结 语

本文结合基于互联网的控制系统需求,采集了网络化实时控制场景RTT时延样本,对采集样本的短时间窗口统计特性进行分析,并使用混合威布尔模型表征短时间窗口RTT时延特性,计算结果验证了所提出混合威布尔模型的有效性。虽然混合威布尔模型能够很好地表征短时间窗口RTT时延特性,但不同区间窗口RTT时延参数的转移规律及其与整体RTT时延混合模型参数的关系等问题仍不明朗,未来研究工作将围绕窗口间RTT时延参数转移规律及预测模型的选择展开。

表2 混合威布尔模型参数及K-S检验结果

[1] CIUCU F, BURCHARD A, LIEBEHERR J. A network service curve approach for the stochastic analysis of networks [C]∥Proceedings of the 2005 ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems. New York, USA: ACM, 2005: 279-290.

[2] 韩悦, 刘增基, 姚明旿. 基于指数上鞅的统计端到端时延分析 [J]. 计算机学报, 2012, 35(10): 2016-2022. HAN Yue, LIU Zengji, YAO Mingwu. Exponential supermartingale for the stochastic analysis of end-to-end delay [J]. Chinese Journal of Computers, 2012, 35(10): 2016-2022.

[3] NG T E, ZHANG H. Predicting internet network distance with coordinates-based approaches [C]∥Proceedings of the Twenty-First Annual Joint Conference of the IEEE Computer and Communications Societies. Piscataway, NJ, USA: IEEE, 2002: 170-179.

[4] ZHANG B, NG T S E, NANDI A, et al. Measurement based analysis, modeling, and synthesis of the internet delay space [C]∥Proceedings of the 6th ACM SIGCOMM Conference on Internet Measurement. New York, USA: ACM, 2006: 85-98.

[5] PADMANABHAN V N, SUBRAMANIAN L. An investigation of geographic mapping techniques for internet hosts [C]∥Proceedings of the ACM SIGCOMM Computer Communication Review. New York, USA: ACM, 2001: 173-185.

[6] 林川, 赵海, 毕远国, 等. 互联网网络时延特征研究 [J]. 通信学报, 2015(3): 167-178. LIN Chuan, ZHAO Hai, BI Yuanguo, et al. Research on network delay of Internet [J]. Journal on Communications, 2015(3): 167-178.

[7] 李超, 赵海, 张昕, 等. Internet中支配延迟的特征行为研究 [J]. 电子学报, 2008, 36(6): 1063-1067. LI Chao, ZHAO Hai, ZHANG Xin, et al. Research on the characteristic behavior of internet dominant delay [J]. Acta Electronica Sinica, 2008, 36(6): 1063-1067.

[8] MARKOPOULOU A, TOBAGI F, KARAM M. Loss and delay measurements of internet backbones [J]. Computer Communications, 2006, 29(10): 1590-1604.

[9] GEARY R. Relative efficiency of count of sign changes for assessing residual autoregression in least squares regression [J]. Biometrika, 1970, 57(1): 123-127.

[10]REDNER R A, WALKER H F. Mixture densities, maximum likelihood and the EM algorithm [J]. SIAM Review, 1984, 26(2): 195-239.

[11]ZHANG L, GOVE J H, LIU C, et al. A finite mixture of two Weibull distributions for modeling the diameter distributions of rotated-sigmoid, uneven-aged stands [J]. Canadian Journal of Forest Research, 2001, 31(9): 1654-1659.

[12]JIANG R, MURTHY D. Mixture of Weibull distributions-parametric characterization of failure rate function [J]. Applied Stochastic Models and Data Analysis, 1998, 14(1): 47-65.

[13]HERNANDEZ J A, PHILLIPS I W. Weibull mixture model to characterise end-to-end Internet delay at coarse time-scales [J]. Proceedings of Communications, 2006, 153(2): 295-304.

[本刊相关文献链接]

翟永惠,吴江,王鼎.采用时延估计的外辐射源雷达杂波抑制算法.2015,49(12):47-52.[doi:10.7652/xjtuxb201512008]

王文博,汪斌强,王志明,等.针对控制平面连通效能优化的控制器布置方法.2015,49(12):77-82.[doi:10.7652/xjtuxb 201512013]

巴斌,郑娜娥,朱世磊,等.利用蒙特卡罗的最大似然时延估计算法.2015,49(8):24-30.[doi:10.7652/xjtuxb201508005]

王丽霞,曲桦,赵季红,等.软件定义网络中应用二值粒子群优化的控制器部署策略.2015,49(6):67-71.[doi:10.7652/xjtuxb201506011]

吴杰,冯祖仁,刘恒,等.水下目标多元声传感阵列网络定位方法.2015,49(4):40-45.[doi:10.7652/xjtuxb201504007]

李季碧,邓科,任智,等.机会网络中高效低时延多摆渡节点路由算法.2015,49(4):91-97.[doi:10.7652/xjtuxb201504 015]

王云龙,吴瑛.联合时延与多普勒频率的直接定位改进算法.2015,49(4):123-129.[doi:10.7652/xjtuxb201504020]

李季碧,李宾,任智,等.自适应动态功率控制的机会网络节能高效路由算法.2014,48(12):49-56.[doi:10.7652/xjtuxb 201412008]

陈倩倩,张磊,徐刚,等.利用多通道联合稀疏重建的干涉逆合成孔径雷达三维成像算法.2014,48(12):100-106.[doi:10.7652/xjtuxb201412016]

李建东,郑杰,刘勤,等.异构协作网络中采用令牌漏桶的多接入业务分配算法.2014,48(8):7-11.[doi:10.7652/xjtuxb 201408002]

刘胜,荆奇.时滞TCP网络滑模预测主动队列管理算法.2014,48(8):42-46.[doi:10.7652/xjtuxb201408008]

李建东,姜建,刘鑫一.采用时延限制和资源预测的异构无线网络选择策略.2014,48(2):74-79.[doi:10.7652/xjtuxb 201402013]

徐剑,倪宏,邓浩江,等.改进的时延约束Steiner树算法.2013,47(8):38-43.[doi:10.7652/xjtuxb201308007]

邵必林,边根庆,张维琪,等.采用k-均值聚类算法的资源搜索模型研究.2012,46(10):55-59.[doi:10.7652/xjtuxb2012 10010]

高昂,李增智,赵季中.用于无线自组织网络的属性加密算法.2012,46(8):33-36.[doi:10.7652/xjtuxb201208006]

任向隆,安建峰,高德远,等.低功耗片上网络映射的遗传及蚂蚁融合算法.2012,46(8):65-70.[doi:10.7652/xjtuxb 201208012]

梁庆伟,姚道远,巩思亮.一种保障时延能量高效的无线传感器网络路由协议.2012,46(6):48-52.[doi:10.7652/xjtuxb 201206009]

(编辑 武红江)

Measuring, Analyzing and Modeling of RTT Delay for Internet-Based Networked Control Systems

YU He1,QIN Guihe1,2,SUN Minghui1,2,LI Bin1,WU Xingchen1

(1. College of Computer Science and Technology, Jilin University, Changchun 130022, China; 2. Key Laboratory of Symbolic Computation and Knowledge Engineering for the Ministry of Education, Changchun 130022, China)

A mixture Weibull model for short window RTT delay is proposed to obtain an accurate model to describe the delay distribution of real-time Internet remote control systems by measuring and analyzing short window round-trip delay(RTT). The model meets real-time requirements of network control systems, has the ability to describe the randomized clustering feature for non-stationary short window RTT delay, and uses the expectation-maximization(EM) algorithm to estimate component densities and parameters of the model. Experimental results confirm the efficiency and precision of 2-mixture Weibull model for the short window RTT delay, and a K-S test shows an acceptable result that the model matches the sample. It is concluded that the model provides a more accurate reference model for optimal control of Internet real-time remote control systems.

round-trip time delay; internet-based NCSs; mixture Weibull distribution; expectation maximization algorithm

2015-10-09。

于赫(1982—),女,博士生;孙铭会(通信作者),男,讲师。 基金项目:吉林省重点科技攻关资助项目(20150204034GX);国家自然科学基金青年科学基金资助项目(61300145);中国博士后科学基金面上资助项目(2014M561294);吉林省科技发展计划资助项目(201303050191GX)。

时间:2015-12-09

10.7652/xjtuxb201602005

TP393

A

0253-987X(2016)02-0026-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151209.1635.006.html