几类分形曲面的构造及其性质

栗 兴 琴

(南京财经大学 应用数学学院,江苏南京 210023)



几类分形曲面的构造及其性质

栗 兴 琴

(南京财经大学 应用数学学院,江苏南京 210023)

分形曲面是R3中的一个分形集.通常，它的构造与分形函数密切相关.本文主要研究几类分形曲面的构造方法及其性质，并给出一些数值例子，说明分形曲面与原始曲面间的关系.

迭代函数系；分形插值函数；分形曲面；性质

分形曲面在计算机图形学、材料学、地震学等许多实际领域有广泛的应用.很多学者已经研究了通过迭代函数系统(IFS)或递归迭代函数系统(RIFS)来构造分形曲面，这些分形曲面都是某个IFS或RIFS的吸引子.谢和平等人[1-2]提出了一种在矩形域构造分形插值曲面的数学模型.Massopust[3]给出了三角区域上分形插值曲面的构造方法，为了保证得到的分形曲面的连续性，附加了边界上插值节点共面的条件.Malysz[4]构造了一种IFS，并证明其存在唯一的吸引子，且这个吸引子是经过某个数据点集的连续二元函数的图像.对矩形域上任意插值节点的情形，Feng等人[5]在IFS中引入了函数纵向尺度因子，保证了分形插值曲面的连续性.文献[6-7]中，作者讨论了隐变量二元分形插值曲面的构造问题.文献[8]研究了利用递归分形函数和Lipschitz函数来构造分形曲面，并计算了它的盒维数. Wang等人[9]基于实数的康托级数表示，构造了一类粗糙曲面，同时，给出曲面分形维数的计算公式.文献[10]在矩形域上使用具有变量自由参数的IFS，构造了一类新的分形插值曲面，并研究了这类曲面的若干性质.文献[11]给出了在矩形网格上构造分形插值曲面的一般方法，并研究了对插值点和纵向尺度因子没有任何要求的双线性分形插值曲面.

本文研究基于几类已知的FIF来构造的分形曲面的剖分，讨论这几类分形曲面的若干性质.给出几个数值例子，展示分形曲面与原始曲面之间的关系.

1 分形插值函数

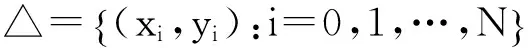
(1.1)

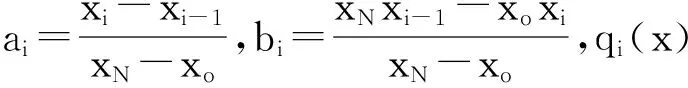
根据Barnsley定理[12],上述IFS{K;Wi,i=1,2,…,N}有唯一一个吸引子G，且G是定义在I上的某个连续函数g的图像，满足g(xi)=yi,i=0,1，…，N.该函数g称为FIF，它是唯一一个满足下列不动点方程的函数：

它的图像G经过给定的数据集△.通常，g是处处连续而处处不可微的,一般具有非整数的维数.

设f∈C(I)，在式(1.1)中，考虑

qi(x)=f∘Li(x)-αib(x),

(1.2)

其中b:I→R是连续映射，且满足了

b(xo)=f(xo),b(xN)=f(xN),b≠f.

这里插值数据是

{(xi,f(xi)):i=0,1,…,N}.

由Barnsley定理可知，存在一个FIFfα满足:

fα(xi)=f(xi)，i=0,1,…,N,

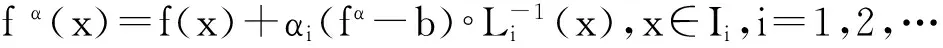
N·fα称为与f对应的α-FIF.特别地，当

b=Lf，

(1.3)

其中L:C(I)→C(I)是线性有界算子，并满足

(Lf)(xo)=f(xo)，(Lf)(xN)=f(xN),L≠Id(单位算子)

称此时的FIFfα是与L和△有关的FIF.

命题1.1[13]对任意的f∈C(I),设

|α|∞=max{|αn|:n=1,2,…,N}，

fα是由IFS(1.1)-(1.3)确定的FIF，则有

由于具有常数纵向尺度因子的IFS在迭代过程中，使得各个分割子区间上具有相同的纵向压缩比，这样产生的FIF通常具备较明显的自相似特征，因而在拟合某些自相似性较弱的不规则数据和非光滑曲线的过程中缺乏一定的灵活性.因此，若将(1.1)中的常数尺度因子αi均变成函数尺度因子αi(x)，相应得到的FIF更具有灵活性.此时，命题1.1中的

|α|∞=max{|αn(x)|,x∈I,n=1,2,…,N}.

命题1.2[14]对任意f∈C(I)，且f(x)≥0，∀x∈I.令

mi=min{f(x):x∈Ii}，M*=max{b(x):x∈I}.

若αi∈C(I),i=1,2,…,N,满足

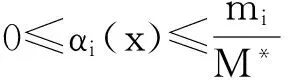
则相应的FIFfα∈C(I)且fα(x)≥0,∀x∈I.

命题1.3[14]设f∈C(I),考虑式(1.1)中的αi∈C(I)，i=1,2,…,N,

qi(x)=f(Li(x))-αi(x)b(x)，b(xo)=f(xo),b(xN)=f(xN),

若αi(x)≥0,b(x)≥f(x),∀x∈I成立，则有

fα(x)≤f(x),∀x∈I.

命题1.4[15]给定p∈N和数据集

{ynk:n=0,1,…,N;k=0,1,…,p},

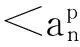
g(k)(xn)=ynk,n=0,1,…,N;k=0,1,…,p,……

此时(1.1)式中的qn(x)(n=1,2,…,N)是阶数最高为2p+1的多项式.

命题1.4中给出的FIF被称为是Hermite分形插值函数(HFIF).

命题1.5[15]设(fα)(k),(fβ)(k)分别是fα和fβ的k阶导数(0≤k≤p),则有

其中

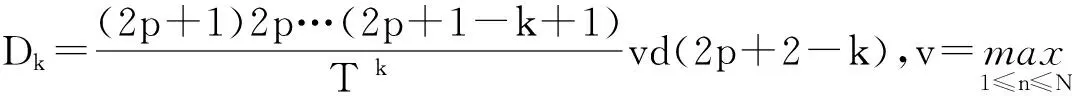
Pn为关联矩阵的逆矩阵，

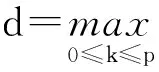
2 分形曲面的构造及性质

设gα,hα:I→R是两个分形函数，λ,μ:I×I→R是两个二元Lipschitz函数，定义二元函数

F：I×I→R，F(x,y)=λ(x,y)gα(x)+μ(x,y)hα(y)

(2.1)

由文献[8]可知，式(2.1)确定的函数是一个二元分形函数，即F(x,y)的图像是一个分形曲面.记

G(x,y)=λ(x,y)g(x)+μ(x,y)h(y),

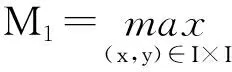
定理2.1 设函数g,h∈C(I),则有

证明 由命题1.1可得，对任意的(x,y)∈I×I，

|F(x,y)-G(x,y)| =|λ(x,y)gα(x)+μ(x,y)hα(y)-λ(x,y)g(x)-μ(x,y)h(y)|

≤|λ(x,y)gα(x)-λ(x,y)g(x)|+|μ(x,y)hα(y)-μ(x,y)h(y)|

=|λ(x,y)|·|gα(x)-g(x)|+|μ(x,y)|·|hα(y)-h(y)|

注2.1 若式(2.1)中的两个分形函数分别取为gα(x),hβ(y),它们分别是对应于纵向尺度因子α，β的FIF，则有

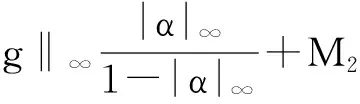
定理2.2 对任意g,h∈C(I),且g(x),h(x)≥0,∀x∈I.令

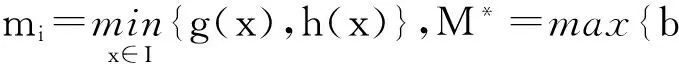
若αi∈C(I),i=1,2,…,N,满足

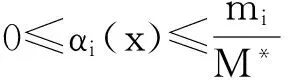
λ(x,y),μ(x,y)≥0,(x,y)∈I×I,

则由式(2.1)确定的分形曲面F(x,y)≥0.

证明 由命题1.2可得，分别与g(x),h(y)对应的FIFgα(x),hα(y)≥0,x∈,y∈I,又因为λ(x,y),μ(x,y)≥0，所以有

F(x,y)=λ(x,y)gα(x)+μ(x,y)hα(y)≥0.

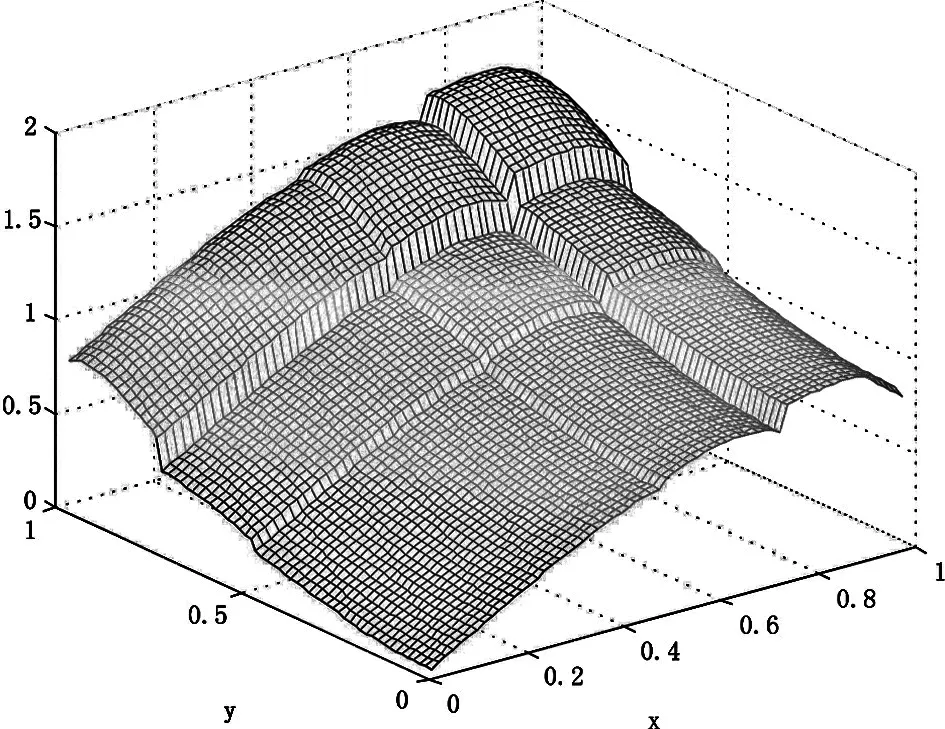
图1

定理2.3 设gα,hα分别是对应于函数g,h∈C(I)且由IFS(1.1)-(1.3)生成的带有函数尺度因子αi=αi(x)的α-FIF.若

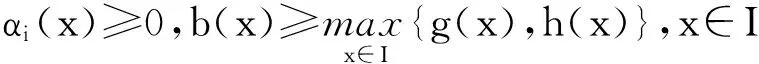
则有

F(x,y)≤G(x,y),(x,y)∈I×I.

证明 由命题1.3可得

gα(x)≤g(x),hα(y)≤h(y),x∈I,y∈I,

所以

F(x,y)=λ(x,y)gα(x)+μ(x,y)hα(y)≤λ(x,y)g(x)+μ(x,y)h(y)=G(x,y),(x,y)∈I×I.

注2.2 若令定理2.3中的

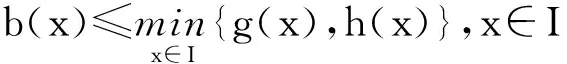
则同理可得

F(x,y)≥G(x,y),(x,y)∈I×I.

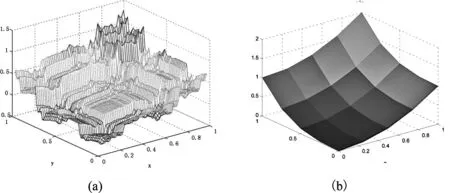
图2

定义2.1 若式(2.1)中的gα,hα分别是由命题1.4确定的HFIF，则称相应的F(x,y),(x,y)∈I×I为Hermite分形曲面.

定理2.4 若λ，μ∈Cp(I×I)，则由定义(2.2)给出的Hermite分形曲面F(x,y)∈Cp(I×I).

证明 由命题1.4可知gα,hα∈Cp(I),因为

F(x,y)=λ(x,y)gα(x)+μ(x,y)hα(y),

所以对∀(x,y)∈(I×I),

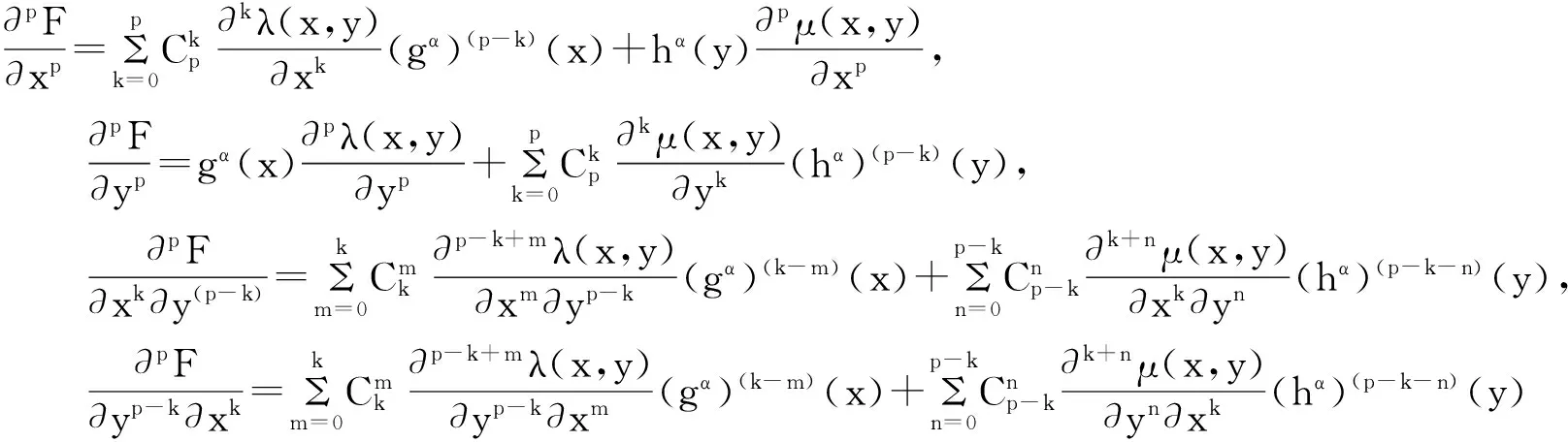
又因为λ，μ∈Cp(I×I)，所以λ，μ的各阶偏导数连续且有下式成立：

故

且F(x,y)的各阶偏导数连续，从而有

F(x,y)∈Cp(I×I)

定理2.5 设gα,hα和gβ,hβ分别是对应于比例因子α和β的HFIF，令

F1(x,y)=λ(x,y)gα(x)+μ(x,y)hα(y),

F2(x,y)=λ(x,y)gβ(x)+μ(x,y)hβ(y)

则

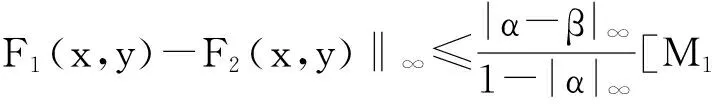
其中D0=(2p+2)vd.

证明 由命题1.5可得，∀(x,y)∈(I×I)，

|F1(x,y)-F2(x,y)| =|λ(x,y)gα(x)+μ(x,y)hα(y)-λ(x,y)gβ(x)-μ(x,y)hβ(y)|

≤|λ(x,y)gα(x)-λ(x,y)gβ(x)|+|μ(x,y)hα(y)-μ(x,y)hβ(y)|

≤|λ(x,y)|·‖gα(x)-gβ(x)‖∞+|μ(x,y)|·‖hα(y)-hβ(y)‖∞

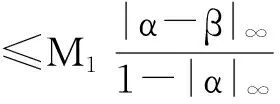
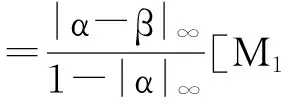
所以，

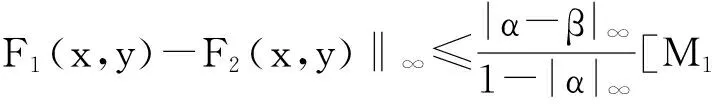
3 结论

本文研究了几类分形曲面的构造问题.给出了基于α-分形曲线和Hermite分形曲线的分形曲面的构造方法，并讨论了它们的一些性质.给出了几个例子说明了分形曲面与其相应的原始函数之间的关系. 本文的研究对粗糙曲面的数值拟合与逼近等实际应用领域有一定的参考价值.

[1]Xie H, Sun H. The study on bivariate fractal interpolation functions and creation of fractal interpolated surfaces[J].Fractals,1997,5(4):625-634.

[2]Xie H, Sun H, Ju Y, Feng Z. Study on generation of rock fracture surfaces by using fractal interpolation[J].Internat. J. Solids Structures, 2001,38(32):5765-5787.

[3]Massopust P R. Fractal surfaces[J].J Math Anal Appl,1990(151):275-290.

[4]Malysz R. The Minkowski dimension of the bivariate fractal interpolation surfaces[J].Chaos,Solitons&Fractals,2006,27(5):1147-1156.

[5]Feng Z,Feng Y,Yuan Z.Fractal interpolation surfaces with function vertical scaling factors[J].Appl Math Letters, 2012,25(1):1896-1900.

[6]Chand A K B,Kapoor G P.Hidden variable bivariate fractal interpolation surface[J].Fractals,2003,11(3):277-288.

[7]Kapoor G P, Prasad S A. Smoothness of coalescence hidden-variable fractal interpolation surface[J].Int J Bifurcation Chaos: APP. Sci. Eng,2009,19(7):2321-2333.

[8]Chol-hui Yun, Hyong-chol O, Hui-chol Choi.Construction of fractal surfaces by recurrent fractal interpolation curves[J].Chaos,Solitons&Fractals,2014,66(1):136-143.

[9]Wang H Y,Xu Z B.A class of rough surfaces and their fractal dimensions[J].J Math Anal Appl, 2001,259(2):537-553.

[10]王宏勇，杨守志.具有变量自由参数的分形插值曲面的构造与性质[J].数学学报，2014,57(2)：223-234.

[11]Ruan H J,Xu Q.Fractal interpolation surfaces on rectangular grids[J].Bull Aust Math Soc, 2015，91(3)：435-446.

[12]Barnsley M F.Fractal functions and interpolation[J].Constr Approx,1986,2(1):303-329.

[13]Viswanathan P,Chand A K B.Fractal rational functions and their approximation properties[J].J ApproxTheory,2014,185(11):31-50.

[14]Viswanathan P, Navascuès M A,Chand A K B. Associate fractal functions inLp-spaces and in one-sided uniform approximation[J]. J Math Anal Appl, 2016(433):862-876.

[15]Navascués M A, Sebastián M V. Generalization of Hermite functions by fractal interpolation[J].J ApproxTheory,2004,131(1):19-29.

Constructions and Properties of Several Kinds of Fractal Surfaces

LI Xing-qin

(School of Applied Mathematics, Nanjing University of Finance & Economics, Nanjing 210023, China)

A fractal surface is a fractal set in R3. Generally, the constructions of fractal surfaces are closely related to the fractal functions. The methods of constructions and properties of several kinds of fractal surfaces are investigated in the present paper. Furthermore, several numerical examples are given, which illustrate the relationships between the fractal surfaces and their original functions.

iterated function system; fractal interpolation function; fractal surfaces; properties

2016-09-15

栗兴琴(1990-)，女，山东临沂人，南京财经大学应用数学学院硕士研究生.

O174.4

A

1672-2590(2016)06-0052-06