利用混合模型方法建立海南省橡胶树立木材积方程

陈振雄，贺东北，贺 鹏

（国家林业局中南林业调查规划设计院，湖南 长沙 410014）

利用混合模型方法建立海南省橡胶树立木材积方程

陈振雄，贺东北，贺 鹏

（国家林业局中南林业调查规划设计院，湖南 长沙 410014）

橡胶树立木材积是全国林业常用数表体系的重要组成部分，目前由于多方面原因，我国无省级尺度以上的橡胶树立木材积表。海南省是我国橡胶树的主要种植区域，编制橡胶树立木材积表，将填补海南乃至全国基础林业数表的空白。编制二元立木材积表通常采用以胸径（D）、树高（H）为变量的山本材积式方程，未考虑区域分布、经营状况及品系等因素影响。由于橡胶树在经营中普遍采取了截干分枝措施，不同区域范围的立地条件、经营状况也不尽相同，加之橡胶树品系较多，均会给橡胶树材积带来一定程度的差异。为综合考虑这些因素的影响，以山本材积式方程为基础，分析了橡胶树分枝数、区域、品系对立木材积方程的影响，利用混合模型方法建立考虑上述因素为随机效应的立木材积混合模型。研究结果表明：橡胶树品系对立木材积的影响不显著，而分枝数、区域对立木材积的影响显著；建立考虑分枝数、区域及分枝数与区域交互作用为随机效应的混合模型明显优于山本材积式模型，其拟合优度、预估精度更高，适应性更强。

材积；非线性混合模型；山本材积方程；橡胶树；海南省

森林是陆地生态系统的主体[1-2]，是经济社会可持续发展十分重要的物质基础，是保障国土生态安全、改善生态环境、维持人类与生物圈生态平衡的重要保障，在应对全球气候变化中具有不可替代的作用。衡量森林资源数量多少的主要指标之一就是森林蓄积，而立木材积表是计量森林蓄积必不可少的“度量衡”。橡胶树作为重要的工业原料和战略物资[3]，其种植区域主要分布在我国的海南、云南、广东和广西4省（区），以海南省种植面积最大。由于受多方面因素影响，我国及相关省（区）均未建立或颁布橡胶树立木材积表。海南省橡胶树也一直沿用广东省1978年建立的天然阔叶树立木材积表，由于橡胶材积计算结果与实际存在较大偏差，给林业生产经营管理带来了诸多困难。因此，建立与海南省当地林分结构和林木生长过程相适应的橡胶树立木材积方程是十分迫切必要的，编制橡胶树立木材积表，将填补海南省乃至全国基础林业数表的空白。

编制立木材积方法较多，其中以二元山本材积式模型应用最为常见，能较好体现干形随胸径(D)和树高(H)变化的规律，在生产实践中普遍认为适用性好、精度较高的模型[4]。有学者以山本材积式为基础，还进一步对提高模型拟合效果与适用性进行了探索研究，骆期邦、曾伟生等[5]在山本材积式的基础上，构建了可变参数山本模型；党永峰[6]、张连金等[7]运用山本材积式采用分段拟合的方法建立材积模型；除独立建立材积方程外，曾伟生[8]、陈振雄等[9]综合考虑材积与生物量、重量的相容性建立联立方程组，采用度量误差模型方法建立相容性材积模型；赵浩彦等[4]以山本材积式为基础，综合考虑林分密度、年龄等因子对材积的影响，建立了多元混合效应材积模型。上述改进模型与常规山本材积式相比，拟合效果更好，模型精度更高。

海南省橡胶树在生产经营中，普遍将树干在离地面约2 m高处密节芽下方采取了截干措施，以促进植株萌生疏朗的分枝，采取截干措施后的林木主干生长状况与分枝数量与未采取截干措施的林木存在差异，一定程度上对相同胸高条件下的立木材积造成影响。按《中国国家地理》[10]的分类，海南岛地理气候分为湿润、干旱、半干旱半湿润等区域，不同区域呈现明显不同气候特征，加之橡胶树经营品系繁多，不同区域、品系的橡胶树生长状况也存在差异。因此，为分析上述因素对海南省橡胶树立木材积的影响，本研究利用非线性混合模型方法建立考虑上述因素为随机效应的立木材积模型，以期为建立更具适应性的通用性立木材积方程提供新方法。

1 数据与采集

1.1 样本组织

数据来自2014年海南省橡胶树常用数表研建项目，共采集橡胶树样木217株，胸径按径级采样分别为6 cm、10 cm、16 cm、22 cm、28 cm、≥32 cm 6个取样点，每个取样点样木株数控制在35株左右。在每个径级点取样时，根据各径阶树高的实际变化幅度按低、中、高（以高径比控制）选取样木，并记录每株样木分枝数量。样木覆盖海南省东部湿润区、中部山区和西部干旱区 6县（市），其中琼中（56株）、儋州（23株）、白沙（32株）、保亭（30株）、琼海（46株）和澄迈（30株）。样木按品系分，有PRIM600（100株）、PR107（83株）、IAN873（34株）。样木具体情况详见表1。

表1 海南省橡胶树样木情况表Table 1 General situations of standing volume trees sample of rubber tree in Hainan province

1.2 数据采集

样木数据采集基本方法是，先将选定的样木进行伐前胸径（D）、地径、10 cm和1.5 m高度处直径测量，伐倒后量测树干高度（H）、树干相对高0.05H，0.1H，0.2H，0.3H，0.4H，0.5H，0.6H，0.7H，0.8H，0.9H处带皮直径。当橡胶树采取了截干措施，优先以分叉直径较大、最高（最长）的分叉枝条作为样木的主干，当枝条大小无明显差异时，选择与底部树干垂直延长平面最接近的枝条作为主干。其它分枝如果基部直径≥10 cm且枝条高度≥2 m的，将其作为一株完整林木按照上述要求进行数据采集。橡胶树干直径因割胶破坏的，取上、下等距离处保存完好的树干直径的平均值或直接采用树干去皮直径加树皮厚度作为相应树干直径。

1.3 材积求算

树干材积采用区分求积法[9]计算，公式如下：

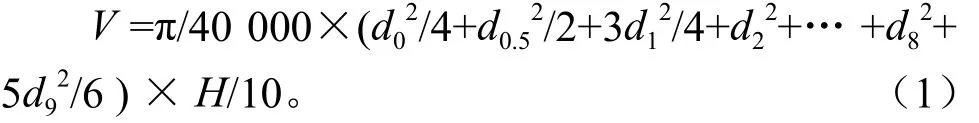
式（1）中：di（i＝ 0，0.5，1，2，…，9）分别表示0，0.5/10，1/10，2/10，…，9/10（H）处的带皮直径（cm）；H为树高（m）；π取 3.141 59。样木存在分枝时，样木总材积为主干材积与分枝材积之和。

2 建模方法

2.1 山本材积式

以胸径（D）和树高（H）为自变量，采用山本材积式建立海南省橡胶树二元材积模型，模型结构为[5,9,11]：

式（2）中：V为材积（m3），D为胸径（cm），H为树高（m），ai为模型参数。

2.2 非线性混合模型

混合模型是同时包含固定效应变量和随机效应变量的模型[12]。将海南省橡胶树林木胸径（D）、树高（H）等直接测量因子解释的材积变动称为固定效应变量，分枝数、区域、品系及其交互影响等非测量因子（Z）解释的材积变动称为随机效应变量。建立同时包含固定效应变量和随机效应变量的橡胶树二元立木材积方程混合模型的基本结构[13]为：

式（3）中：V为材积（m3），ai为固定效应参数，ui为随机效应参数，zi为反映橡胶树分枝数、区域及品系的随机效应变量。其中，随机效应参数ui的数学期望相互独立，且值为0，即E(ui)=0，cov(ui，uj)=0(i≠j)，随机效应参数ui是否与0在统计学上存有显著差异，可通过随机效应的显著性检验得出。如果随机效应参数与0在统计学上无显著性差异，说明该随机效应变量对橡胶树的立木材积影响没有显著差异，可在建立的模型中舍去该随机效应变量。

为分析橡胶树分枝数、区域、品系及其交互作用的随机影响，将分枝数分为3个类型，无分枝、一个分枝、两个及以上分枝，类型代码分别为0、1、2；区域分布涉及白沙、保亭、澄迈、儋州、琼海和琼中6个县（市），类型代码分别为1、2、3、4、5、6；品系为 PRIM600、PR107、IAN873，类型代码分别为1、2、3。

2.3 模型评价

为分析建立的模型优劣，采用如下模型检验评价指标[9，14]进行评价：相关系数(R2)、平均预估精度（P）、估计值的标准误差(SEE)、平均预估误差(MPE)、平均百分标准误差（MPSE）、总相对偏差（TRB）和平均系统偏差（MSB）。计算公式如下：

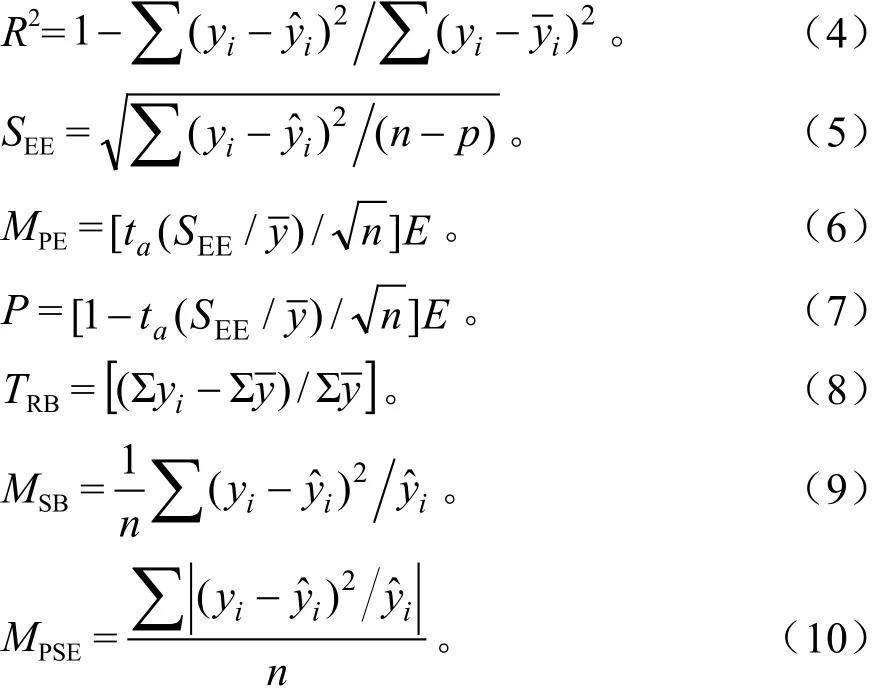
式（4）～（10）中：n为样本单元数，p为参数个数，ta为置信水平α时的t值，yi和分别为样本的实测值和预估值，为样本平均值。

R2、SEE是回归模型评价的常用指标，P、MPE可视为总体水平上平均估计值的精度指标，MPSE可视为估计单木水平估计值的精度指标，TRB、MSB是反映方程总体拟合效果的重要指标，在二元材积模型中一般要求控制在±3%范围以内，趋近于0时说明拟合效果最好。

3 结果与分析

3.1 分枝数、区域及品系的随机效应分析

将橡胶分枝数为随机效应变量的模型称为混合模型1，将区域为随机效应变量的模型称为混合模型2，将品系为随机效应变量的模型称为混合模型3，3个混合模型固定参数a0、a1、a2对应的随机效应参数分别为u0、u1和u2。表2为3个混合模型的拟合结果。

从表2中可以看出，以品系为随机效应变量的混合模型，对应的u0、u1和u23个随机参数，其随机效应均不显著，与0在统计上无显著性差异；以分枝数、区域为随机效应变量的混合模型，u1、u22个随机参数的随机效应不显著，与0在统计上无显著性差异，但分枝数、区域作为随机效应变量对固定参数a0的随机参数u0随机效应显著，其中分枝数达极显著水平（0.01水平），区域达显著水平（0.05水平）。对固定参数a0的随机效应，从分枝数情况来看，无分枝数的为负，有分枝数的为正，说明相同胸高条件下，有分枝的橡胶树林木立木材积一般要大于无分枝的林木材积；从区域分布来看，相同胸高条件下，橡胶树立木材积从大到小依次为琼中、澄迈、保亭、儋州、琼海、白沙县。

表2 橡胶树分枝数、区域及品系分别作为随机效应变量的混合模型拟合结果†Table 2 Fitting results of nonlinear mixed effect models by using rubber tree branches, regional and strains as random effects variables

3.2 考虑分枝数、区域为随机效应的混合模型拟合结果

根据上面的分析，随机效应变量分枝数、区域对山本材积式固定参数a0的随机效应显著。因此，建立综合考虑分枝数、区域以及分枝数与区域的交互影响作为固定参数a0的随机效应的混合模型。固定参数a0的随机效应构造为：u1+u2+u1·u2，其中u1、u2分别代表分枝数、区域的随机主效应，u1·u2代表分枝数与区域的交互作用效应。建立的混合模型（模型5）与常规山本材积式（模型4）拟合结果见表3、表4，其中表4为分枝数与区域的交互影响随机参数值。

从表3可以看出，以分枝数、区域及分枝数与区域的交互作用为随机效应变量的混合模型，其随机参数在统计上均达极显著水平（0.01水平），与0存在显著差异。建立的混合模型拟合效果较好，调整R方为0.972，高于常规山本材积式的0.963，SEE为0.052，低于常规山本材积式的0.059。

表3 以分枝数、区域作为随机效应变量的混合模型拟合结果Table 3 Fitting results of nonlinear mixed effect models by using rubber tree branches and regional as random effects variables

表4 分枝与区域交互效应参数估计值†Table 4 The interaction random effects parameters estimates of nonlinear mixed effect models by using rubber tree branches, and regional variables

3.3 混合模型与山本材积式拟合结果比较

为进一步比较建立的混合模型与常规山本材积式模型的拟合效果，采用了TRB、MSB、MPSE、P分径阶、分区域进行了检验，得到的结果分别见表5、表6。绘制了混合模型、山本材积式模型得到的材积残差散点分布图（图1）。

从比较结果中可以看出，总体上来看，混合模型的TRB、MSB、MPSE明显低于山本材积式模型，总体预估精度P比山本材积式高0.32%，TRB的绝对值低0.07%，混合模型预估值更趋近于实际值。混合模型各径阶、各区域预估精度均明显高于山本材积式，各径阶最大提高1.64%，各区域最大提高2.51%。混合模型各径阶、区域的TRB在3.8%以内，而山本材积式的TRB最大达7.02%。比较结果说明混合模型比山本材积模型的拟合优度和精度更高，模型具有更好的适应性。

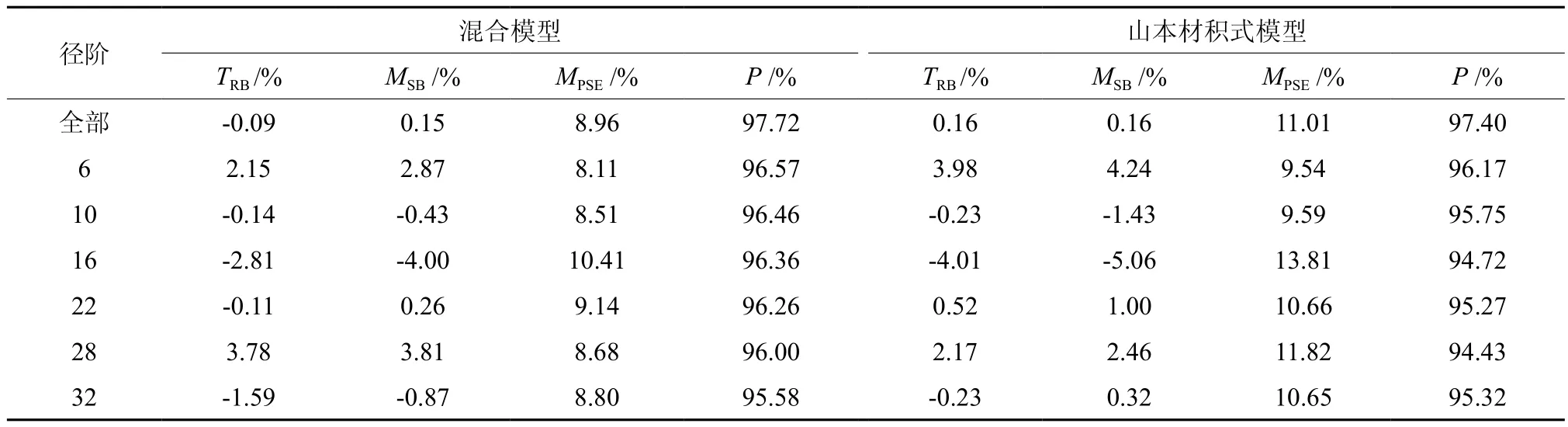
表5 混合模型与山本材积式模型分径阶检验结果一览Table 5 Comparison of test results between nonlinear mixed effect model and Yamamoto standard volume equations by diameter classes

表6 混合模型与山本材积式模型分区域检验结果一览Table 6 Comparison of test results between nonlinear mixed effect model and Yamamoto standard volume equations by region

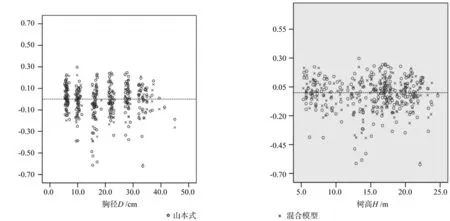
图1 橡胶树材积相对残差随胸径（D）树高（H）分布Fig.1 Rubber tree volume relative residuals errors with DBH (D) height (H) distribution

4 结论与讨论

以海南省橡胶树种为例，通过利用非线性混合模型方法，分析了橡胶树截干分枝数、区域分布、品系对立木材积的影响，研究建立了以分枝数与区域为随机效应的橡胶树立木材积混合模型，并将建立的混合模型与常规二元山本材积式进行了对比分析，研究结果表明：

（1）不同橡胶树品系对二元立木材积的随机效应不显著，而分枝数、区域对二元立木材积固定参数a0随机效应显著，而对固定参数a1、a2的随机效应不显著。

（2）建立综合考虑分枝数、区域及分枝数与区域相互影响为随机效应的混合模型，得到海南省橡胶树立木材积方程预估精度（P）、复相关系数（R2）均高于常规山本式材积式模型，分径阶、区域检验得到的结果均明显优于常规山本材积式模型。

（3）采用混合模型方法建立材积模型，不仅考虑了林木属性因子（胸径、树高）对材积的作用，还考虑了经营措施（截干分枝）、地理条件对材积的作用，模型更能适应不同情况下的立木材积估算，为提高林木材积估算精度及建立不同尺度范围的通用性立木材积模型提供了有效途径。

总之，利用混合模型方法建立的材积模型，与常规二元山本材积式相比，拟合效果更好，精度更高，在不同区域范围更具适应性。本研究建立的橡胶树立木材积方程，其总体预估精度均在97%以上，各径阶总相对偏差基本控制在3%以内，建立的材积模型完全可应用于橡胶树立木材积的估计。

[1]陈振雄,熊智平,曾伟生,等.基于大样地双重抽样方法的广东省森林资源监测研究[J],中南林业调查规划,2014,33(3):28-33.

[2]曾伟生.二元立木材积方程的检验与更新方法探讨[J],中南林业调查规划,2010,29(3):1-5.

[3]李国华,田耀华,倪书邦,等.橡胶树生理生态学研究进展[J]生态环境学报,生态环境学报,2009,18(3):1146-1154.

[4]赵浩彦,张洁,张民侠,等.南京地区马尾松多元混合效应材积模型研建[J]. 中南林业科技大学学报,2015,35(12):40-45.

[5]骆期邦,曾伟生,贺东北.林业数表模型理论、方法与实践[M].长沙:湖南科学技术出版社,2001.

[6]党永峰,王雪军,曾伟生.用分段建模方法建立东北落叶松立木材积和生物量方程[J],林业科学研究,2012, 25(5): 558-563.

[7]张连金,曾伟生,唐守正.用带截距的非线性方程和分段建模方法对立木生物量估计的比较［J］.林业科学研究,2011,24(4): 453 -457.

[8]曾伟生,姚顺彬,肖前辉.中国湿地松立木生物量方程的研建[J].中南林业科技大学学报,2015,35(1):8-13.

[9]陈振雄,贺东北,丁长春.利用度量误差模型方法建立海南省桉树、木麻黄、马占相思重量与材积相容性模型[J].中南林业调查规划, 2013, 32(4):4-11.

[10]单之蔷.中国国家地理:海南专辑[M],北京:《中国国家地理》杂志社,2013.

[11]曾伟生.立木生物量建模方法[M].北京:中国林业出版社,2011.

[12]曾伟生,唐守正.利用混合模型方法建立全国和区域相容性立木生物量方程[J].中南林业调查规划, 2010, 29(4):1-6.

[13]曾伟生.我国杉木通用性立木生物量模型研究[J].中南林业调查规划, 2013, 32(4):4-11.

[14]陈振雄,贺东北,肖前辉.海南省桉树、木麻黄、马占相思削度方程研建[J].中南林业调查规划, 2012,31(3):11-14.

Using mixed-effects modeling method to establish standing volume equations for rubber tree in Hainan province

CHEN Zhen-xiong, HE Dong-bei, HE Peng
(Central South Forest Inventory and Planning Institute of State Forestry Administration, Changsha 410014, Hunan, China)

The standing rubber tree volume is an important part of the national standing forestry volume table system. Due to multiple aspects, the provincial scale above standing rubber tree volume hasn’t been established yet. Hainan province is the major rubber tree planting area in china, to establish the standing rubber tree volume would fi ll the gap of basic standing forestry volumes in Hainan, even in the whole country. The principle method to establish the standing volume is Yamamoto volume equation with tree diameter（D）and height（H）as variables，without considering the in fl uence of regional distribution, site conditions, the strains of rubber tree and other aspects. Due to the fact that rubber trees are generally taken cut stem measures, the diverse of site conditions and management status in different regions, and the variety strains of rubber tree, which will bring a certain degree of difference to standing rubber tree volume.Taken these factors into consideration, this paper analyzed these factors’ in fl uence upon the standing rubber tree volume in Hainan province based on Yamamoto volume equation, to establish nonlinear mixed effects models for standing volume by using factors above as random effects variables. The results showed that: the strains of rubber tree does not have a signi fi cant impact on the parameters of Yamamoto volume equation, but the branch numbers and the planting region have a signi fi cantly affection; the nonlinear mixed effects standing volume model has better fi tting results, higher accuracy, and better adequacy than the Yamamoto standard volume model.

standing volume；nonlinear mixed-effects model; Yamamoto standard volume equations; rubber tree; Hainan province

S794.1

A

1673-923X(2016)12-0031-06

10.14067/j.cnki.1673-923x.2016.12.006

http: //qks.csuft.edu.cn

2016-01-15

省林业厅重点项目“海南省加勒比松橡胶树常用数表研建”（HNHJ2014-11-007）

陈振雄，高级工程师，硕士研究生；E-mail：9120512@qq.com

陈振雄，贺东北，贺 鹏. 利用混合模型方法建立海南省橡胶树立木材积方程[J].中南林业科技大学学报，2016, 36(12):31-36.

[本文编校：文凤鸣]