基于k-NN算法的叶面积指数遥感反演

孙 华，罗朝沁 ，林 辉 ，严恩萍 ，罗喜华 ，罗孝云

(1.中南林业科技大学 林业遥感信息工程研究中心，湖南 长沙 410004；2.攸县黄丰桥国有林场，湖南 攸县 412300)

基于k-NN算法的叶面积指数遥感反演

孙 华1，罗朝沁1，林 辉1，严恩萍1，罗喜华2，罗孝云2

(1.中南林业科技大学 林业遥感信息工程研究中心，湖南 长沙 410004；2.攸县黄丰桥国有林场，湖南 攸县 412300)

叶面积指数（Leaf Area Index，LAI）作为植被冠层结构的重要描述参数之一，能体现植被光合、蒸腾和呼吸作用的能力。借助GPS和LAI-2200冠层分析仪在攸县黄丰桥林场开展LAI测量。利用ENVI软件对GeoEye-1 数据进行了辐射定标，大气校正和正射校正。通过研究LAI与GeoEye-1影像波段及其衍生指数的相关性，筛选出2组估算LAI的指数因子（6个指数因子和10个指数因子）。应用k-NN进行叶面积指数反演，同时将反演结果与多元线性回归模型结果进行比较。结果表明：利用2组指数因子进行多元线性回归模型反演LAI中，6个指数因子的模型决定系数R2为0.386，10个指数因子的模型决定系数R2为0.498。从回归模拟的角度分析，10个指数因子得到的模拟结果要优于6个指数因子的模拟结果。利用2组指数因子通过设置4个不同的k值（k=3，5，7，10）得到8个k-NN反演结果中，以10个指数因子得到的k-NN反演结果较好，其中在k=3时效果最好，其决定系数R2为0.733，精度为85.4%。建模精度分析表明选用10个指数因子进行LAI的反演优于选用6个指数因子，其中k-NN方法的反演结果优于多元线性回归模型，说明利用k-NN方法进行LAI的反演是可行的。

林业遥感；叶面积指数；k-NN；GeoEye-1；黄丰桥林场

叶面积指数（leaf area index，LAI）是指单位地表面积上单面绿叶面积的总和[1-3]，是描述植被冠层结构的一个重要参数，近年来越来越受到重视。小范围内的叶面积指数测定一般采用实测方法[4]进行，尽管实测方法能够提供比较精确的LAI，但是只能获取样地（点）上的数据，很难得到大范围叶面积指数的空间分布，应用范围受到了限制。遥感技术可以提供不同空间尺度的遥感影像数据，为大范围内叶面积指数反演提供了强有力的数据支持，通过建立统计模型[2-4]或冠层物理模型[4-8]进行叶面积指数估算，得到不同分辨率的各类LAI数据产品。

叶面积指数冠层物理模型方法主要包括几何光学模型[4-9]，辐射传输模型[10-11]，神经网络[12]，贝叶斯网络[13]，遗传算法[14]，查找表法[15]以及几何光学模型与辐射传输模型的综合[2]等。几何光学模型，辐射传输模型以及二者的综合模型具有较强的物理基础和普适性，需要较多的地面辅助参数[16]。神经网络一种高效的机器学习方法，模型的反演速度很快，但是需要大量的样本进行训练才能得到较可靠的反演结果[12]。神经网络和查找表法是近年来发展起来的通用方法，能很好的将反射率与需要反演的生物物理参数有效的联系起来，但需要建立大型模拟数据库。此外，遗传算法与贝叶斯网络在叶面积指数反演具有一定的潜力，但在区域范围内的应用中还有待检验。统计模型法主要是通过分析遥感影像各波段反射率，植被指数及其衍生指数与叶面积指数的关系，建立统计模型，这类方法比较简单直接[17-18]。但是统计模型法所建立的回归模型往往带有经验性，换一个研究区或应用一个新的数据源，模型参数需要重新调整，模型的普适性和推广性不强。此外，回归模型分析的基础是假设遥感数据或者植被指数与需要反演的物理参数（如叶面积指数）存在线性关系，其次，回归模型假设用于建模的自变量之间是不相关的，但是实际情况并非如此，遥感影像不同的波段之间具有一定的相关性，因此非参数方法如k-NN可能是除回归分析方法之外一种较好的选择。以GeoEye-1影像为数据源，采用k-NN方法开展攸县黄丰桥林场叶面积指数反演，并对不同条件下所得反演结果进行比较，旨在分析非参数估计的特点，为区域范围内的叶面积指数高效反演提供一种方法参考。

图1 研究区位置Fig. 1 Location of study area

1 研究区概况

黄丰桥国有林场呈带状，横跨株洲市攸县东西部，以中低山貌为主，介于 113°04′～ 113°43′E，27°06′～ 27°04′N 之间（图 1）。主要成土母岩为板页岩，土壤以板页岩发育而成的山地黄壤为主。东北部与江西的莲花、萍乡交界，东南与茶陵县接壤，西北部与株洲、醴陵毗邻。全场地貌以中低山为主，境内最高海拔1 270 m，最低海拔115 m，坡度介于20 °～35 °之间。林场地处中亚热带季风湿润气候区，年均气温17.8 ℃；平均无霜期为292 d。现有林地总面积10 122.6 hm2，主要以杉木为主，森林覆盖率为86.24%[18]，此次研究的范围主要包括广黄，柏市和长岭3个分场，面积约150 km2。

2 材料与方法

2.1 数据处理

2.1.1 遥感数据处理

研究所用的遥感影像数据为GeoEye-1，包括4个多光谱波段和1个全色波段，数据获取时间为2013年3月12日。全色波段空间分辨率为0.41 m，多光谱波段包括红、绿、蓝、近红外等4个波段，空间分辨率为1.65 m。GeoEye-1数据处理主要包括辐射定标，大气校正和正射校正。为了得到与地面实测样地一致的坐标，采用天宝 Trimble GEO XH 3000高精度GPS，进行野外差分定位，共采集42个控制点坐标信息，用于GeoEye-1数据的正射校正，正射校正后的影像点位误差在2 m以内。

2.1.2 样地设计与叶面积指数测量

GeoEye-1空间分辨率高，为了使此次调查的数据满足多种分辨率遥感影像开展叶面积指数反演，且相互之间可以验证。对研究区进行系统嵌套抽样，抽样间隔为3 km×3 km，样地设计大小为1 km×1 km，在1 km×1 km样地对角线上设置7个30 m×30 m小样地（图2）。2号，3号小样地中心点位置与1号样地之间水平与垂直方向的距离相距62.5 m；4号，5号小样地中心点位置与1号样地之间水平与垂直方向的距离相距187.5 m；6号，7号小样地中心点位置与1号样地之间水平与垂直方向的距离相距375 m。在每个30 m×30 m小样地内，按6 m的水平间隔设置5个1 m×1 m的小样方。2013年7月15日至8月1日，利用LI-COR公司生产的LAI-2200仪器在每个1 m×1 m的小样方内4个不同的位置测量4次所得的均值作为小样方的叶面积指数值，共获得210个有效叶面积指数测量结果。

图2 样地大小与形状Fig. 2 Plot size and shape

2.2 遥感因子获取

研究在参考已有研究的基础上，结合GeoEye-1数据特点，选用各波段的反射率，归一化植被指数（NDVI），红绿指数（RGVI），比值植被指数（SR）及衍生比值指数，SAVI（L取0.1，0.25，0.35，0.5），一共计算24个变量。

2.3 叶面积指数反演方法

通过计算210个LAI样地的均值和标准差，得到样本的残差分布，剔除了12个离群的样本数据。叶面积指数反演采用线性回归和k-NN2种方法进行。首先，在GIS软件中提取198个样地对应的24个指数值，分析24个建模因子与叶面积指数的相关性，在95%置信区间范围内，利用方差扩大因子（VIF）对建模因子进行共线性诊断，删除VIF值在10以上的变量。对筛选出来的因子，选取3/4的样本量建立叶面积指数回归模型，剩余样本进行精度检验。回归分析采用两种形式，一种是对VIF筛选出来的所有变量建立模型，另一种就是对筛选出来的变量开展逐步回归分析。两种形式所采用的变量都用于k-NN算法模拟。

k-NN方法是一种非参数估计方法，在森林蓄积量、生物量以及胸高断面积等方面开展了较为深入的研究。k-NN方法有两个重要的假设前提。首先，假设遥感影像每个像元的光谱响应值仅与森林分布状况相关，与像元所在的地理位置无关；其次，假设地面样地分布在一个大范围内，并且可视为用于估计其他区域的地面真实数据[4]。有关k-NN方法的定义与推导见文献[19]，文献[20]和文献[21]。

2.4 精度评价

模型或模拟的结果需要进行误差评价，论文选用留置样本法和交叉验证法（Cross-Validation）对叶面积指数模拟结果进行评价。选定决定系数（R2），估测均值，相对平均误差，相对均方根误差，残差标准差等指标对回归分析进行评价。除此之外，采用交叉验证方法进行k-NN模拟的精度验证，即利用k-NN方法每次估计时从地面调查样地样本中剔除一个样地，用k-NN方法产生该样地的估计值，将该样地的估计值与它的地面调查实测值进行比较并计算一个误差。然后，将该样地放回，抽取另一个不同的地面调查样地，再用k-NN产生该样地的估计值，并将该样地的估计值与它的实测值进行比较计算一个误差。重复以上过程直至所有的地面调查样地被估计，并计算这些样地实测值与估计值之间的平方根均方误差。

3 结果与分析

3.1 遥感影像与叶面积指数的相关性分析

对提取的24个变量与叶面积指数进行了相关性分析，在95%可靠性下，利用方差扩大因子（VIF）对建模因子进行共线性诊断，删除VIF值在10以上的变量。NDVI，SR43等10个变量的相关系数在统计上是显著的（表1）。由表1可知，在显著性高的变量中，以NDVI的相关系数最大为0.592，SR43与LAI的相关系数次之，在显著性高的变量中NIR的相关系数最小仅为0.225。

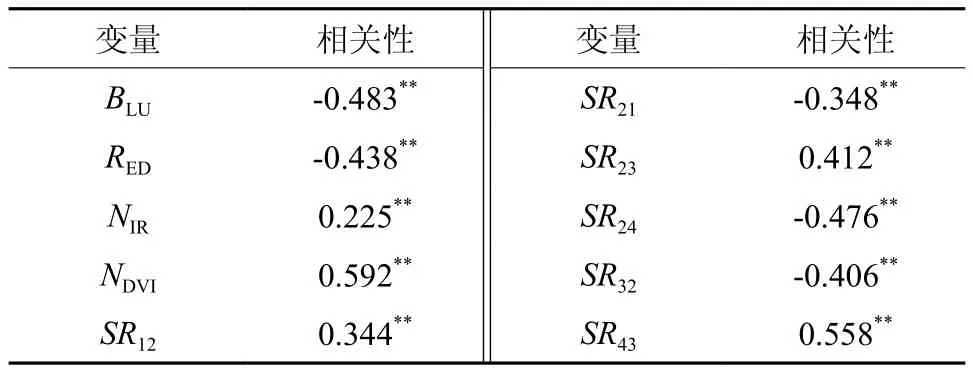
表1 叶面积指数相关性统计Table 1 Correlation of Landsat 8 derived spectral variables with LAI

3.2 回归分析

对筛选出来的因子，选取3/4的样本量建立叶面积指数回归模型，剩余样本进行精度检验。回归分析采用两种形式，一种是对VIF筛选出来的10个变量建立叶面积指数反演模型，另一种就是对筛选出来的变量开展逐步回归分析，最终保留的变量有6个，分别为BLU，RED，NDVI，SR21，SR23，SR24。选取3/4的样本量建立叶面积指数回归模型（式1，式2），剩余样本进行精度检验，分别计算模拟结果与估测结果的相关性，相对平均误差，相对均方根误差，分析估测均值与实测均值的差异，具体结果见表2。从表2可知，10变量的回归模型所得模拟结果与检验数据的相关性高于6个变量的逐步回归分析结果。相对平均误差，相对均方根误差，分析估测均值结果亦是如此。从回归模拟的角度分析，10个变量得到的模拟结果要优于6个变量的模拟结果。

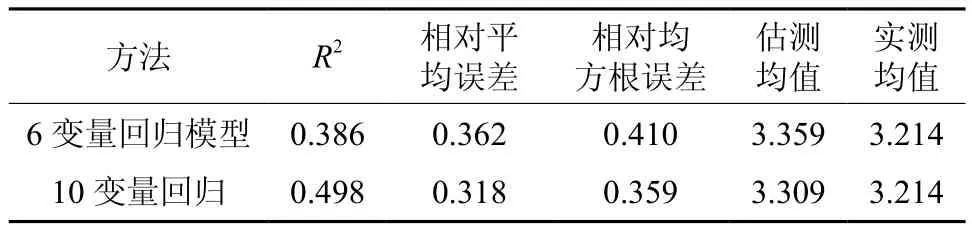
表2 回归分析模拟叶面积指数估计误差Table 2 Error estimation of leaf area index using multiple linear regression model

利用检验数据对模拟结果进行验证，发现预测结果与检验数据存在较好的线性关系，10个变量回归模型的拟合结果要优于6个变量的模型。从模拟结果的残差分布来看，所有数据的残差都在置信带内 [-2 σˆ， 2 σˆ]，残差的随机性分布较好（图3）。利用上述2种回归模型对图像进行模拟，有植被覆盖的地方叶面积指数值得到了较好的模拟结果，从图5（a，b）多元线性回归模拟结果来看，在没有采集样地数据的地方出现了过低估计的现象，估计值结果小于0，与实际状况存在差异。

3.3 k-NN模拟结果分析

回归分析所得的叶面积指数反演结果在植被覆盖区域获得了较好的模拟效果，但是在非植被区出现了过低的估计现象，这与实际情况不相符。为了更好的开展黄丰桥林场的叶面积指数反演工作，研究利用上述回归分析2种模型所采用的变量开展k-NN模拟。为了更准确的体现k-NN算法的模拟效果，将外业采集到的所有有效样地都用于叶面积指数模拟，利用交叉验证法（Cross-Validation）对不同k值大小的叶面积指数模拟结果进行评价，其中k的取值为3、5、7、10，计算相应的结果如表3所示。

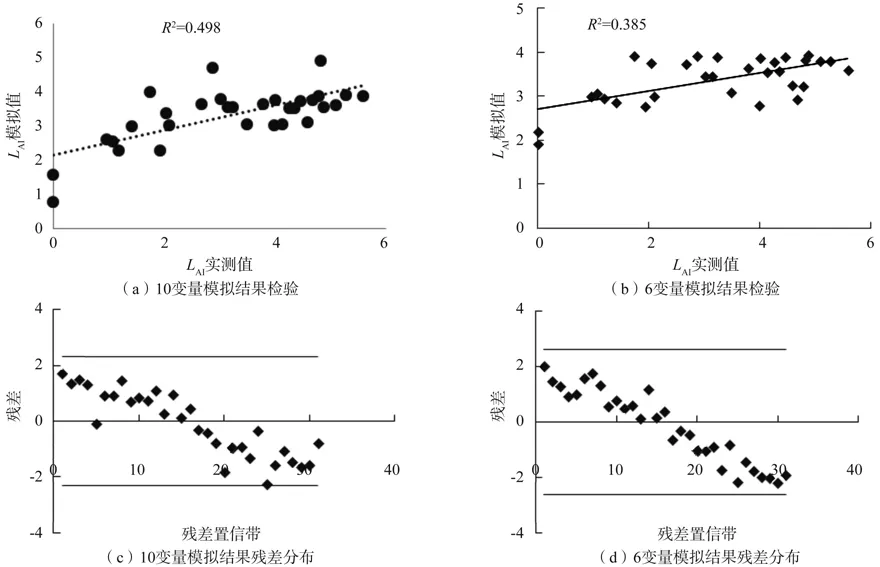
图3 LAI模拟结果与实测值比较Fig.3 Observed values and predicted values of LAI

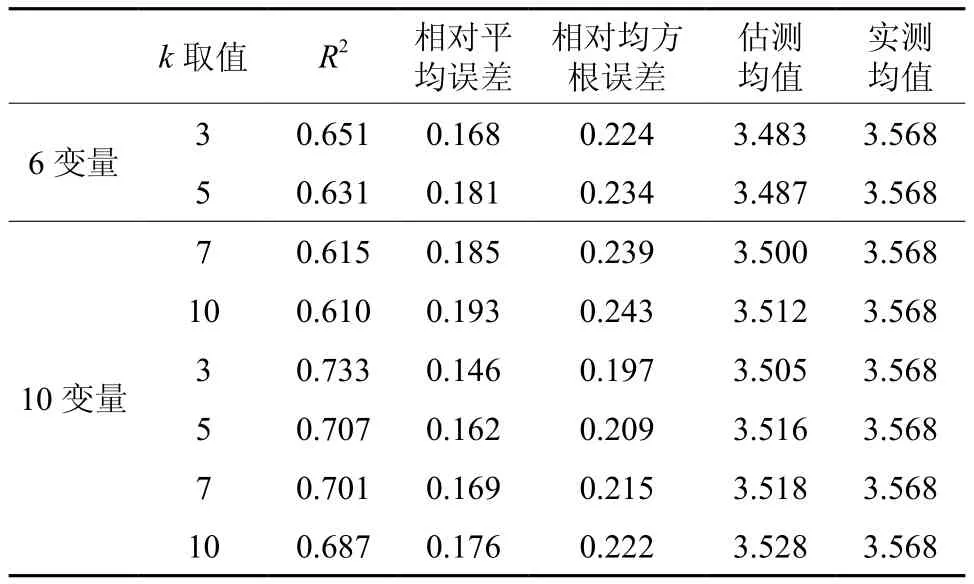
表3 k-NN的叶面积指数估计误差Table 3 Error estimation of leaf area index k-NN

由表3可得：（1）应用6个变量的k-NN方法估测黄丰桥林场的叶面积指数，相对平均误差小于20%，要优于6个变量的回归分析模型，从不同k值大小模拟的结果来看，k为3时，相对平均误差、相对均方根误差是最小的，也是最优的估计结果。（2）应用10个变量的k-NN模拟结果，与6个变量的k-NN模拟结果类似，k值变大，估计结果与实测结果的相关性减少，当k为10时最小，绝对系数为0.687，从统计的角度分析，k为10的模拟结果依然可靠；（3）应用10个变量的k-NN模拟结果在k值相同时，其模拟结果与实测数据的相对平均误差、相对均方根误差均小于应用6个变量的k-NN模拟结果。相关系数的分析结果也是如此，说明采用k-NN进行叶面积指数模拟时，参与模拟的变量越多，模拟结果与真实值越接近。（4）从模拟效果来看，k为3时，应用6个变量和10个变量的模拟结果均是各自模拟结果中效果最好的。

模拟结果的交叉验证主要是检验模拟结果与实测值是否存在较好的线性关系，分析各验证样地的残差是否落在置信带内 [-2 σˆ，2 σˆ]。从图4可知，当k值为3时，6个变量和10个变量的k-NN模拟结果与实测值均存在良好的线性关系，决定系数（R2）分别为0.651，0.733。从残差的分布图来看，模拟结果的残差随机性分布大部分落在置信带区间内，但是10个变量的残差随机性分布更为合理。从图5（c，d）可知，整个研究区叶面积指数反演效果较好，没有出现过低估计的现象，从模拟效果来看k-NN模拟优于回归分析。

图4 k-NN模拟LAI结果与实测值比较（k=3）Fig.4 Observed values and predicted values of LAI using k-NN

图5 黄丰桥林场叶面积指数反演结果Fig.5 Inversion Results of LAI in Huangfengqiao forest farm

4 结论与讨论

论文以GeoEye-1影像为数据源，采用多元线性回归和k-NN方法，结合地面调查数据，开展攸县黄丰桥林场叶面积指数反演。首先分析影像各波段反射率，植被指数及衍生变量与叶面积指数的相关性，筛选出相关性较高的因子，采用方差扩大因子法进一步开展建模因子的共线性诊断，对最终保留的变量，运用多元线性回归和k-NN方法开展叶面积指数模拟，对模拟结果进行精度验证与残差分析，得出以下几点结论。

（1）建模因子的相关性排序分析。波段反射率是地表各地类辐射能量差异的体现，也是运用植被指数开展叶面积指数的物理基础。本次研究参与分析的24个因子中，10个因子在95%的可靠性统计水平上与叶面积指数显著性相关，相关性最大的为NDVI，相关系数为0.592，说明NDVI与叶面积指数具有较强的相关性，其次为SR43为0.558，其余的依次为BLU，SR24，RED，相关系数分别为-0.483，-0.476和-0.438，在显著性高的变量中NIR的相关系数最小仅为0.225。

（2）建立了植被指数与叶面积指数的多元线性模型。利用10个相关性较高的因子，分2种情况建立叶面积指数多元线性模型，一是将10个变量全部用来建立模型，二是采用逐步回归的方式建立叶面积指数模型，逐步回归模型最终只采用了6个因子，分别为BLU，RED，NDVI，SR21，SR23，SR24。2种模型的检验结果表明，检验数据与模拟数据存在较好的线性关系，决定系数（R2）分别为0.498，0.386，从残差分布情况来看，10个变量的多元线性回归结果优于6个变量的模拟结果。但是从整个研究区反演的结果来看，多元线性回归模拟结果在植被区的叶面积指数反演取得了较好的反演效果，但是对非植被区出现了过低估计的现象，在有些区域出现了负值，这与实际情况存在出入。从另一个侧面来讲，多元线性回归对参与模拟的样地取得了较好的反演效果，但是对没有开展样地调查的区域可能存在过低或过高估计。

（3）运用k-NN算法得到了较好的叶面积指数模拟效果。将多元回归模型所采用的6个变量与10个变量，分别进行k-NN模拟，k值大小选择，3，5，7，10四种情况，从模拟结果看，k值越大，模拟结果的相对平均误差、相对均方根误差也随之增加，最大误差基本控制在20%左右，较多元回归分析31.8%的相对平均误差有了很大的改进。从研究区k值大小的模拟结果来看，k为3时，10个变量和6个变量模拟效果最好，模拟结果与实测数据的相关性分别为0.733，0.651。模拟结果残差的分布随机性较好，但是从整个研究区模拟效果比较，10个变量的k-NN模拟结果优于6个变量的模拟效果。本研究结论认为，利用k-NN算法开展黄丰桥林场的叶面积指数反演是可行的，可模拟结果的精度考虑，需要尽可能选择多一些变量，有利于提高模拟的精度。

（4）此次研究涉及的样地采用系统抽样的方式得到，样地类型并没有完全覆盖研究区的所有地类类型，从多元线性回归和k-NN模拟结果来看，模拟结果的误差主要在非森林区域，因此，采用分层抽样方式开展叶面积指数反演是下一步工作的方向。

[1]Thimonier A, Sedivy I, Schleppi P. Estimating leaf area index in different types of mature forest stands in Switzerland: a comparison of methods [J]. European Journal of Forest Research,2010, 129(4): 543-562.

[2]向洪波,郭志华,赵占轻,等. 不同空间尺度森林叶面积指数的估算方法[J].林业科学,2009,45(6):139-144.

[3]范闻捷,盖颖颖,徐希孺,等. 遥感反演离散植被有效叶面积指数的空间尺度效应[J].中国科学:地球科学, 2013,43(2):280-286.

[4]梁顺林,李小文,王锦地,等.定量遥感理念与算法[M].北京:科学出版社,2013.

[5]蔡博峰,绍 霞.基于PROSPECT+SAIL模型的遥感叶面积指数反演[J].国土资源遥感,2007, 19(2):39-43.

[6]Jacquemoud S. Inversion of the PROSPECT+SAIL Canopy Re fl ectance Model from AVIRIS Equivalent Spectra: Theoretical Study[J]. Remote Sensing of Environment. 1993, 44(2-3):281-292.

[7]刘照言,马灵玲,唐伶俐.基于SAIL模型的多角度多光谱遥感叶面积指数反演[J].干旱区地理,2010,33(1):93-98.

[8]陈艳华,张万昌,雍 斌.基于分类知识利用神经网络反演叶面积指数[J].生态学报,2007,27(7):2785-2793.

[9]杨贵军,黄文江,王纪华,等. 多源多角度遥感数据反演森林叶面积指数方法[J]. 植物学报,201045(5):566-578.

[10]徐希孺.遥感物理[M].北京:北京大学出版社,2005.

[11]黄 玫,季劲钧. 中国区域植被叶面积指数时空分布——机理模型模拟与遥感反演比较[J]. 生态学报,2010,30(11):3057-3064.

[12]Xiao Z, Liang S, Wang J,et al.Use of general regression neural network for generating the GLASS leaf area index product from time-series MODIS surface re fl ectance[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 52(1):209-223.

[13]Qu Y, Zhang Y, Wang J. A dynamic Bayesian network data fusion algorithm for estimating leaf area index using time-series data from in situ measurement to remote sensing observations [J].International Journal of Remote Sensing,2012,33(4):1106-1125.

[14]Fang H, Liang S, Kuusk A. Retrieving leaf area index using a genetic algorithm with a canopy radiative transfer model[J].Remote sensing of environment,2003,85(3):257-270.

[15]Fang H, Liang S. A hybrid inversion method for mapping leaf area index from MODIS data: Experiments and application to broadleaf canopies [J]. Remote sensing of environment,2005,94(3):405-424.

[16]Song C. Optical remote sensing of forest leaf area index and biomass[J]. Progress in Physical Geography, 2013,37(1):98-113.

[17]李开丽,蒋建军,茅荣正,等. 植被叶面积指数遥感监测模型[J]. 生态学报,2005,25(06):1491-1496.

[18]孙 华,鞠洪波, 张怀清,等. 三种回归分析方法在Hyperion影像LAI反演中的比较[J].生态学报,2012,32(24):7781-7790.

[19]Halme M, Tomppo E.. Improving the accuracy of multisource forest inventory estimates by reducing plot location error -a multicriteria approach[J].Remote Sensing of Environment, 2001,78(3):321-327.

[20]Tomppo E, Halme M. Using coarse scale forest variables as ancillary information and weighting of variables in k-NN estimation: a genetic algorithm approach [J].Remote Sensing of Environment,2004, 92(1):1-20.

[21]谭一凡,郄广平,王敏姿,等.深圳市建成区森林碳分布估测方法比较研究[J].中南林业科技大学学报,2014,34(11):140-149.

Study on remote sensing estimation of leaf area index based on k-NN algorithm

SUN Hua1, LUO Chao-qin1, LIN Hui1, YAN En-ping1, LUO Xi-hua2, LUO Xiao-yun2
(1.Research Center of Forestry Remote Sensing & Information Engineering Central South University & Technology, Changsha 410004,Hunan, China; 2 Huangfengqiao Forestry Farm of Youxian, Youxian 412300, Hunan, China)

As one of the most important description parameters for forest canopy structure, LAI (Leaf Area Index) has the ability to re fl ect the photosynthesis, transpiration and breathing for vegetation. Accurately mapping LAI often conducted by combining sample plots and remotely sensed images. The objective of this study was to employ k-Nearest Neighbor (k-NN) algorithm to estimate the LAI in Huangfengqiao forest Farm of You County, Hunan province of China using GeoEye-1 images and ground sample plots. In this study, ground measurement of LAI was conducted with the assistant of GPS and LAI-2200 canopy analyzer. The GeoEye-1 images were processed with the correction of radiation, atmospheric and orthographic. Moreover, through the correlation analysis of LAI and GeoEye-1 factors, 2 groups (6 variables and 10 variables respectively) of variables were selected for the estimation of LAI. Finally,k-NN algorithm method was used to simulation LAI, and compared with the multiple linear regression. Results show that multiple linear regression model of 10 independent variables was better than 6 variables.TheR2coef fi cient of the two models were 0.498 and 0.386.With the difference of k value (k=3, 5, 7, 10) and variable numbers (6 and 10), 8 combinations and estimations for LAI were generated.The estimation derived from the combination ofk=3 and 10 variables had greatest accuracy, with theR2of 0.733 and estimation accuracy of 85.4%. This implied that the algorithm of k-NN provided greater potential than multiple linear regression model to map LAI with the combination of sample plots and GeoEye-1 images.

forestry remote sensing; leaf area index; k-NN; GeoEye-1; Huangfengqiao forest farm

S757

A

1673-923X(2016)12-0011-07

10.14067/j.cnki.1673-923x.2016.12.003

http: //qks.csuft.edu.cn

2015-04-20

国家“十二五”863项目：“数字化森林资源监测关键技术研究”（2012AA102001）；中国博士后科学基金项目：林分环境条件下的林木冠幅提取及冠形曲线参数化（2014M562147）

孙 华，副教授，博士；E-mail：sunhuayiwen@126.com

孙 华，罗朝沁，林 辉，等. 基于k-NN算法的叶面积指数遥感反演[J].中南林业科技大学学报，2016,36(12):11-17,36.

[本文编校：文凤鸣]