用于PPP模糊度固定的FCBs产品选站策略研究

陈星宇,李建文,魏绒绒,郭亮亮

(信息工程大学 导航与空天目标工程学院,郑州 450052)



用于PPP模糊度固定的FCBs产品选站策略研究

陈星宇,李建文,魏绒绒,郭亮亮

(信息工程大学 导航与空天目标工程学院,郑州 450052)

随着精密单点定位研究的不断深入和发展,精密单点定位已经由浮点解阶段逐渐发展到整数解阶段,使精密单点定位模糊度固定及相关研究方向成为了当前的研究热点。而FCBs产品又是PPP模糊度固定实现的关键和前提。鉴于当前对FCBs产品生成选站策略研究不充分的情况,本文基于数据完好率、宽巷模糊度残差值和单颗卫星综合数据质量等数据质量评定指标,运用全球格网均匀分布选站方法对计算FCBs产品的跟踪站进行选站。结果表明,运用本文的选站策略进行选站,选取40个站所计算的FCBs产品与选取230个站所计算的FCBs产品精度相当,从而大大缩短了FCBs产品的计算时间。

精密单点定位模糊度固定;FCBs产品;选站策略

0 引 言

精密单点定位(PPP)技术是利用全球若干地面跟踪站的GNSS观测数据计算出的精密卫星轨道和卫星钟差,对单台GPS接收机所采集的相位和伪距观测值进行定位解算,获得高精度的待定点的位置坐标的一种定位方法[1-3]。PPP采用绝对定位的模式,具有不受基线长度限制,作业方便自由、数据处理相对简单等优点,它的实现,大大提高利用GNSS技术进行精确定位操作的灵活性,具有广泛的应用价值。尽管PPP有其独特优越性,但也存在缺陷:模糊度的整数特性被破坏和模糊度初始化时间较长。而其中主要原因是由于PPP模糊度受到非整周偏差(FCBs)的影响,原有模糊度的整数特性被破坏,使得PPP用户无法得到像相对定位技术一样的模糊度固定解[4-6]。其中,FCBs指的是由卫星段和接收机段硬件延迟非校准相位延迟(UPDs)的非整周部分[7]。可以通过服务端跟踪站网估计FCBs值,当用户端进行PPP解算时将FCBs值作为已知量对模糊度进行改正,从而使得PPP获得模糊度固定解。而对于PPP模糊度固定(PPP-AR)而言,FCBs产品是其成功的关键。因此,有必要对用于PPP-AR所需的FCBs产品的计算过程及选站策略进行研究,生成FCBs产品,为国际GNSS监测评估系统(iGMAS)产品用户提供更完善的服务,填补国内iGMAS分析中心FCBs产品生成的空缺。

本文基于数据完好率、宽巷模糊度残差值和单颗卫星综合数据质量等数据质量评定指标,运用全球格网均匀分布选站方法对计算FCBs产品的跟踪站进行选站,同时通过实验分析论证了选站策略的有效性,大大缩短了FCBs产品生成所需的计算时间,提高了FCBs产品的计算效率。

1 星间单差FCBs的计算方法

PPP利用消电离层组合模型消除电离层一阶改正项[8-9]。消电离层组合模型为

(1)

消电离层组合的整周模糊度固定解实际是被拆分成窄巷模糊度解和宽巷模糊度解来求解:

(2)

(3)

(4)

其中〈·〉表示对于所有历元求加权平均值,计算中以卫星对观测弧段为时间跨度。这里定权方式采用依赖高度角方式[5, 14]。

(5)

为了避免接收机FCBs的影响,采用星间单差求解宽巷FCBs.在卫星和之间求差得:

(6)

(7)

方差:

(8)

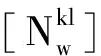
由于宽巷模糊度波长为0.86m,宽巷模糊度较易固定,对宽巷模糊度进行历元间平滑后,就近取整固定宽巷模糊度。当求得宽巷FCBs后,对宽巷模糊度进行固定,当某一观测弧段宽巷模糊度固定成功率低于80%,则在进一步估计宽巷FCBs时不参与计算。

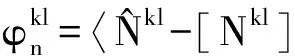
(9)

方差:

(10)

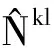
2 FCBs产品的选站策略

2.1 用于计算FCBs的跟踪站数据质量评定指标

2.1.1 数据完好率

因为数据完整率与数据有效率都反映是在计算FCBs过程中,有效历元数与总历元数的比值,对FCBs计算造成的影响相同(造成历元缺失),因此在这里将数据完整率和数据有效率整合,定义为数据完好率。数据完好率是指在规定的观测时段内,数据采样间隔固定的条件下,有效历元数与理论观测历元数的比值,是反映数据完整率和数据有效率综合影响的参数。

2.1.2 宽巷模糊度残差

星间单差宽巷模糊度由式(3)计算可得:

(11)

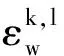
2.1.3 单颗卫星综合数据质量

单颗卫星的数据质量主要包括信噪比、周跳比和多路径效应。

1) 信噪比(SNR)

SNR是指接收的载波信号强度与噪声强度的比值(dBHz)。SNR主要受天线增益参数、接收机中相关器的状态、多路径效应三个方面的影响。

2) 周跳比

周跳比是指在所有观测历元中观测数据数量与周跳数据数量之比。

3) 多路径效应

多路径效应指由于多个路径的信号传播所引起的干涉时延效应[15]。载波相位观测中L1的多路径误差的最大值为4.8cm,对L2载波的多路径误差为6.1cm.而实际上可能有多个反射信号同时进入接收机天线,那么多路径误差将更为复杂。跟踪站选站对站址要求比较高,而且多路径效应主要是影响伪距测量,对载波测量影响较小。

在实际中,综合评价过程就是通过数学模型将多个评价指标“合成”为一个整体性的综合评价指标,本文利用TOPSIS(theTechniqueforOrderPreferencebySimilaritytoIdealSolution)综合评价模型对IGS/iGMAS跟踪站观测数据进行综合评估,流程如图1所示。

通过对测站的观测数据的质量分析,得到对应测站的伪距多径、信噪比和周跳比等指标值,通过对上述指标的筛选以及对指标的正向化和无量纲

化,采用熵值法确定权重系数,利用TOPSIS确定最终的综合评价模型从而得到最终的评价结果[16]。

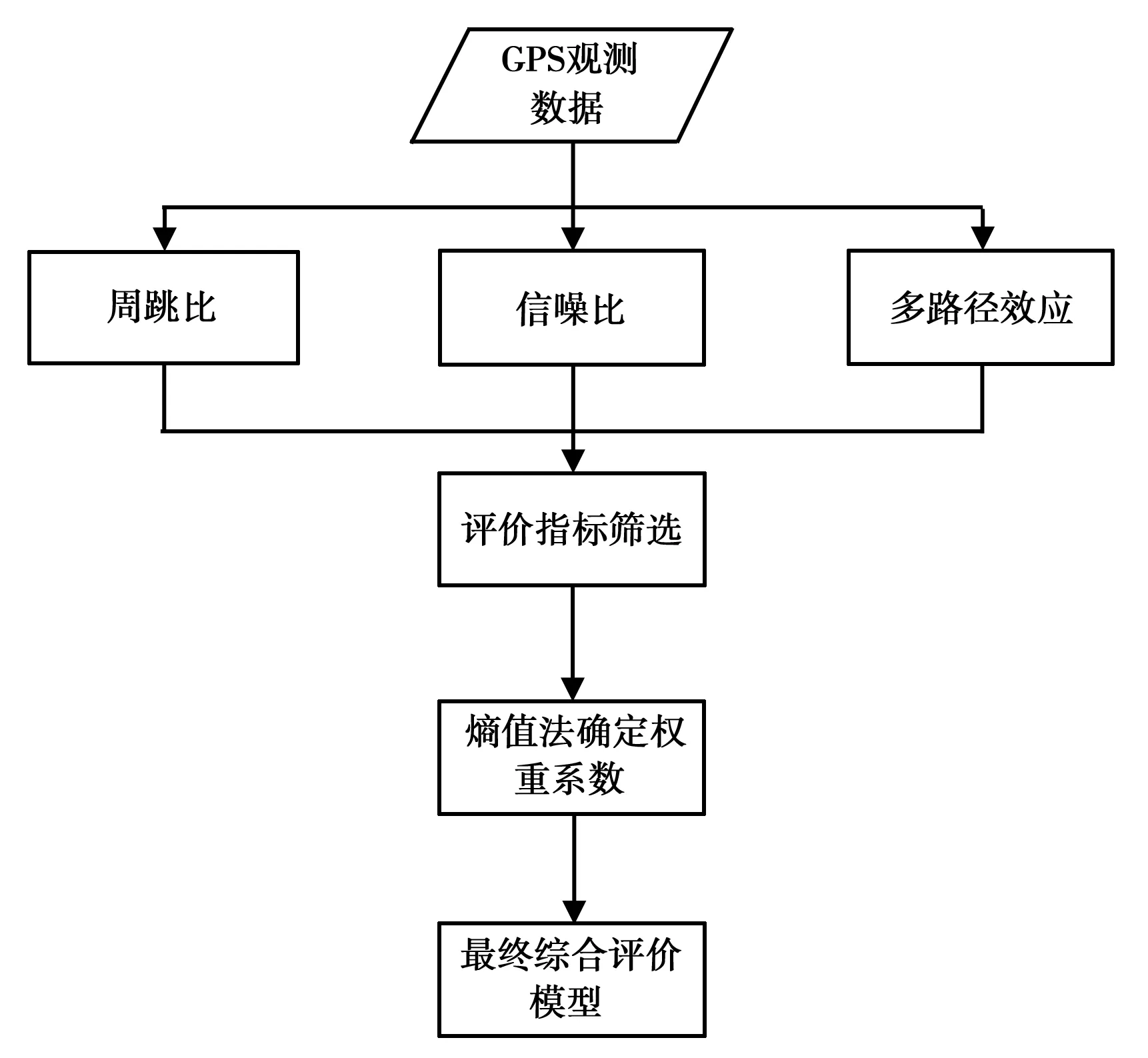
图1 TOPSIS综合评价流程图

2.2 FCBs产品选站策略

以往国内外学者对FCBs产品的生成以及PPP-AR理论方法已经做了比较详细的论述,在文献中提到用于计算全球FCBs产品的跟踪站的数量一般为160个站[5, 17]。葛茂荣在文章中提到过剔除伪距观测质量差的站以及宽巷模糊度固定成功率等指标作为选站的依据,但并没有给出详细的选站策略[5]。本节依据上面介绍的评定参数,对全球所有IGS/iGMAS跟踪的数据进行数据质量分析,利用统计分析的结果选出合适的站的数量。本节所提出的测站选取策略,兼顾数据质量和测站地理分布,并能根据最大使用测站数合理划分经纬度格网,自动选取最优的测站集合。当选定测站数后,全球格网经纬度按进行划分[18],整个测站选取流程如图2所示。

选站步骤如下:

首先,按照前面小节中给定的阈值分别计算宽巷模糊度残差列表、数据完好率列表、和TOPSIS列表,并将三种指标按权比计算得到数据质量综合统计值列表;

其次,按照预先设计的站的数量划分格网,获得格网分区测站列表;

最后,将格网分区测站列表和数据质量综合统计列表综合,按格网逐一选取数据质量好的站,生成最终的测站选站列表。

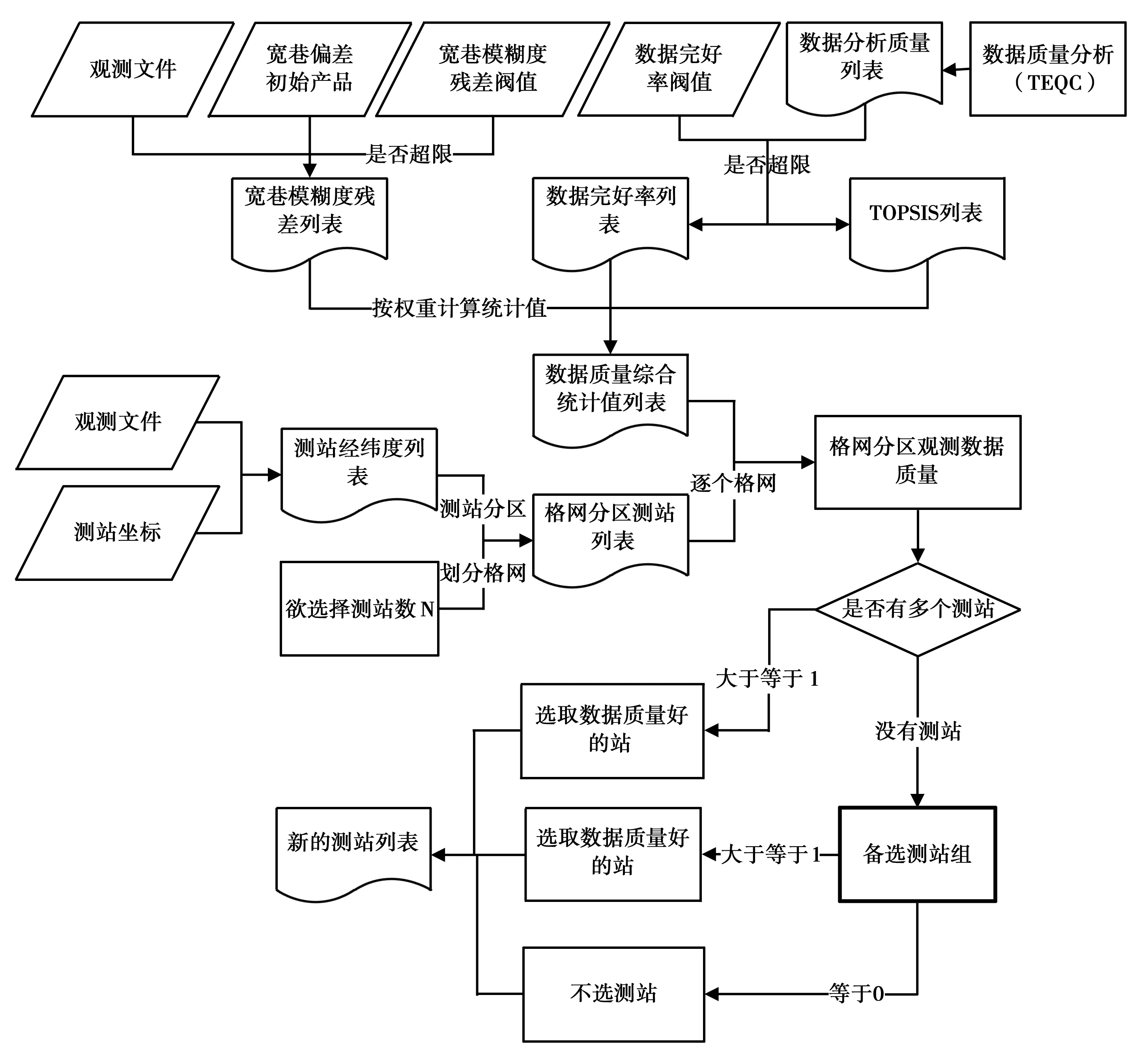
图2 选站策略处理流程

3 FCBs产品选站策略实例分析

为验证测站选取策略的有效性,采用IGS全球观测网和iGMAS跟踪站数据,时间2015年第100天,并设计了4种不同方案:分别选取40、80、230个全球均匀分布的测站进行FCBs产品生产实验。测站全球格网分布情况如图3所示。其中,▲表示方案1的40个测站分布情况,▼表示方案2在方案1基础上增加测站分布情况,○表示方案3在方案2基础上增加的测站分布情况。其中,230个站为数据质量合格的站。40个站和80个站分别按全球格网40和80的数量选出的综合指标好的站。同时给出了312个站的FCBs计算结果。312个站为本论文中IGS/iGMAS为第100天的观测站的总集。

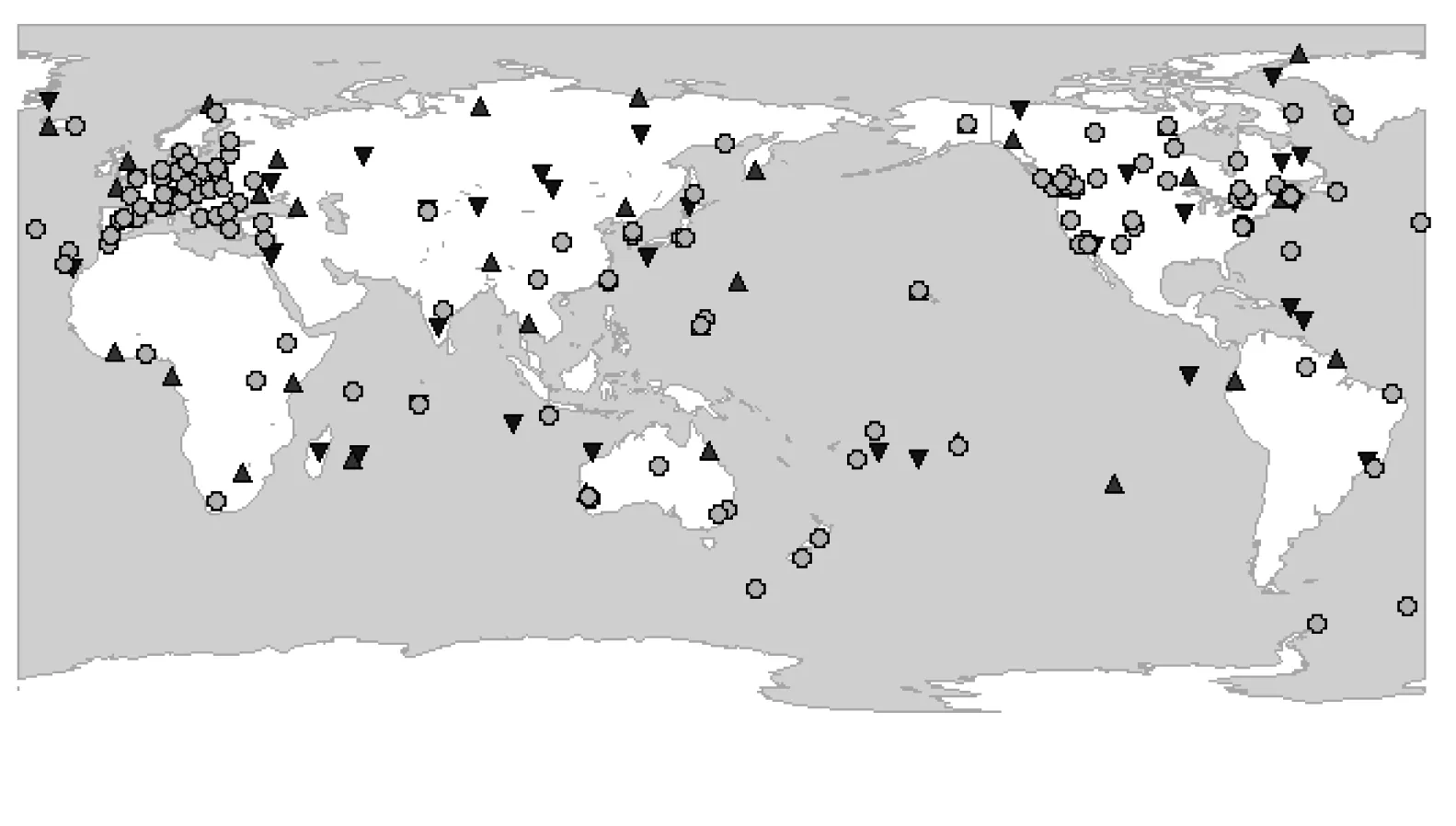
图3 40、80、230个测站全球格网分布情况

从图中可以看出,方案1的全球40个站的选站均匀分布在全球,密度相对较为稀疏。而方案2的80个站的选站策略与方案1相比,在其基础上增加了全球站的分布密度。而方案3的230个所有数据质量合格的站在图中可以看出,部分区域站的密度较大。实际中,IGS跟踪站大部分分布在欧洲和北美洲,而其他地区站的密度相对较为稀疏。通过格网选站可以发现,剔除的站大部分为密度较大的地方的站。具体FCBs产品的计算结果如图4所示。

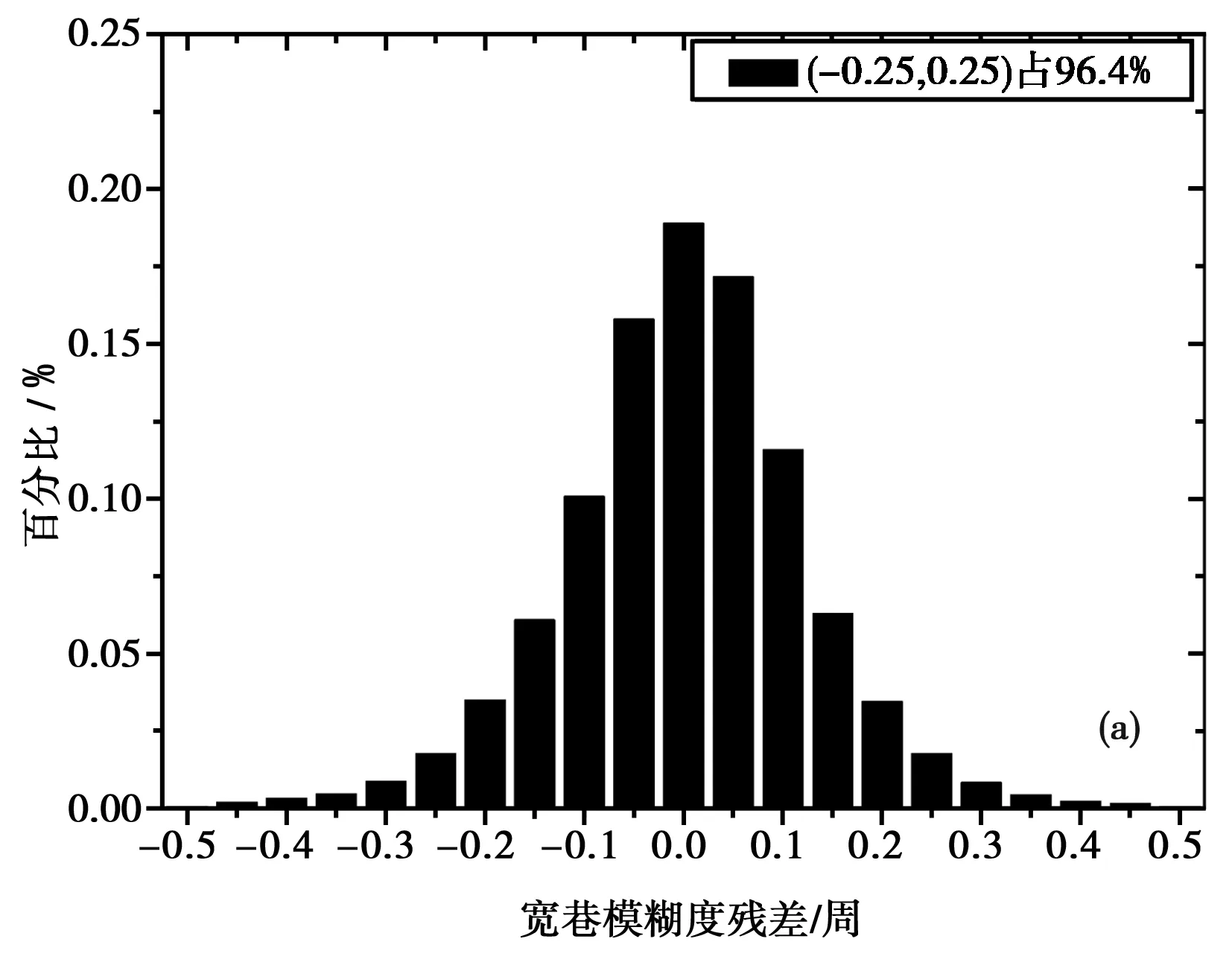
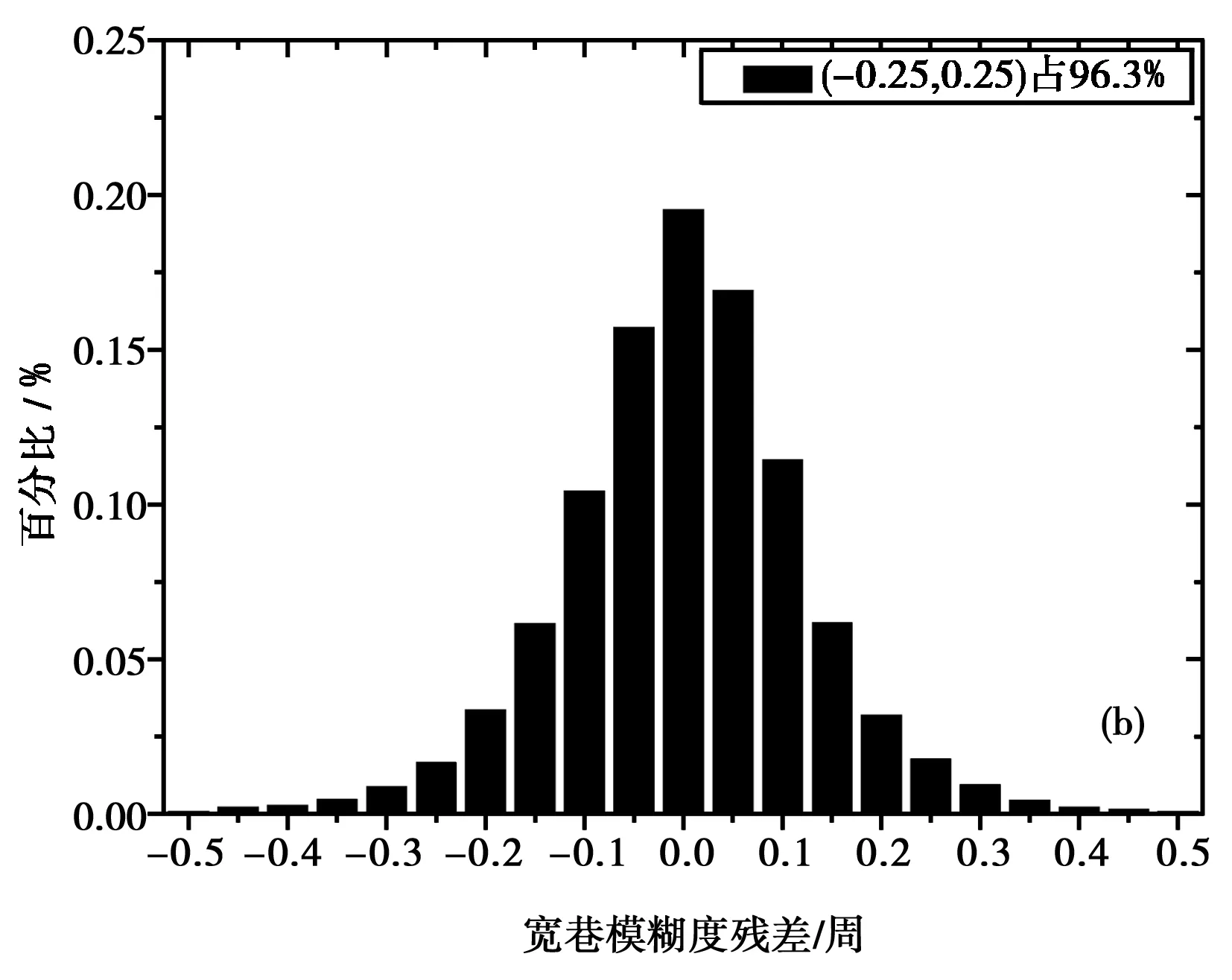
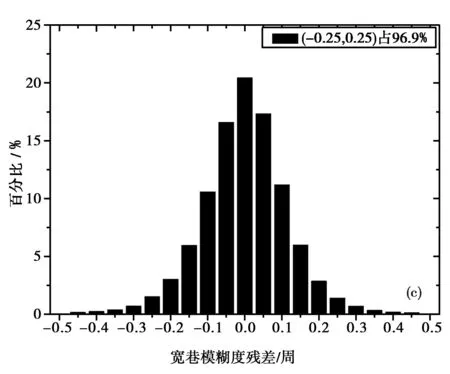
图4 选站数量不同宽巷模糊度残差的频率分布 (a) 40; (b) 80; (c) 230; (d) 312

通过图4(a)～图4(d)可以发现,4种方案宽巷模糊度残差分别96.4%、96.3%、96.9%和94.0%,选站方案数量分别为40、80、230和312个观测站。其中图标题中为了简化,40代表40个站,其他类似。通过图4(a)～图4(c)和图4(d)的比较可知通过设定的选站策略剔除的数据质量较差的站的数据,致使宽巷模糊度残差分布范围有了一定的提高。同时可以发现,图4(a)～图4(d)残差分布情况相似,由于4种方案宽巷模糊度FCBs产品计算结果所采用的算法基本一致。通过对结果进行分析可知,宽巷模糊度FCBs产品,受站数量多少影响较小,40个站、80个站、230个站、312个站数据结果基本一致。因此可知,应用合适的选站策略,宽巷模糊度FCBs产品40个站就可以达到230个站的精度,而对于卫星对宽巷FCBs的完整度如表1所示。

表1 卫星对宽巷FCBs数据完整度

从表中可以发现,尽管40个站的宽巷FCBs产品精度和其他方案的精度相当,但是在一定程度上损坏了卫星对宽巷FCBs的完整度。导致某些卫星对宽巷FCBs值得不到有效的观测,但通过对观测站排查发现,这样的情况一般发生在观测站较少的海上,因此采用40个站进行宽巷FCBs的解算基本可以保障用户的使用。

前面对宽巷模糊度进行了解算和分析,接下来运用各种方案的宽巷FCBs产品进行窄巷FCBs的解算,同宽巷FCBs一样,对窄巷FCBs进行残差统计,统计值如图5所示。

图5(a)～图5(d)分别给出了窄巷模糊度残差值。以上数据是对参与产品计算的站的数据进行窄巷模糊度残差计算。通过上图5(a)～图5(d)可以发现,4种方案窄巷模糊度残差分别87.1%、87.6%、89.1%和81.6%,选站方案数量分别为40、80、230和312个观测站。其中图标题中为了简化,40代表40个站,其他类似。通过图5(a)～ 图5(c)和图5(d)的比较可知通过设定的选站策略剔除的数据质量较差的站的数据,致使窄巷模糊度残差分布范围有了一定的提高。同时可以发现,图5(a)～图5(d)残差分布情况相似,由于4种方案窄巷模糊度FCBs产品计算结果所采用的算法基本一致,数据有共同数据站部分。通过对结果进行分析可知,宽巷模糊度FCBs产品,受站数量多少影响较小,40个站、80个站、230个站、312个站数据结果基本一致。因此可知,窄巷模糊度FCBs产品40个站就可以达到230个站的精度。

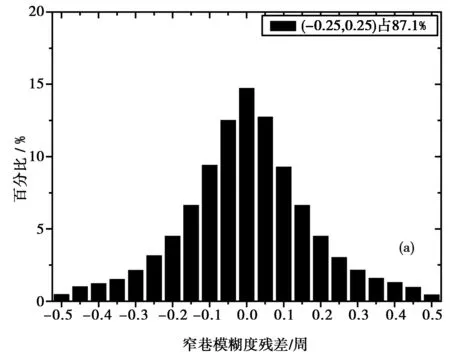
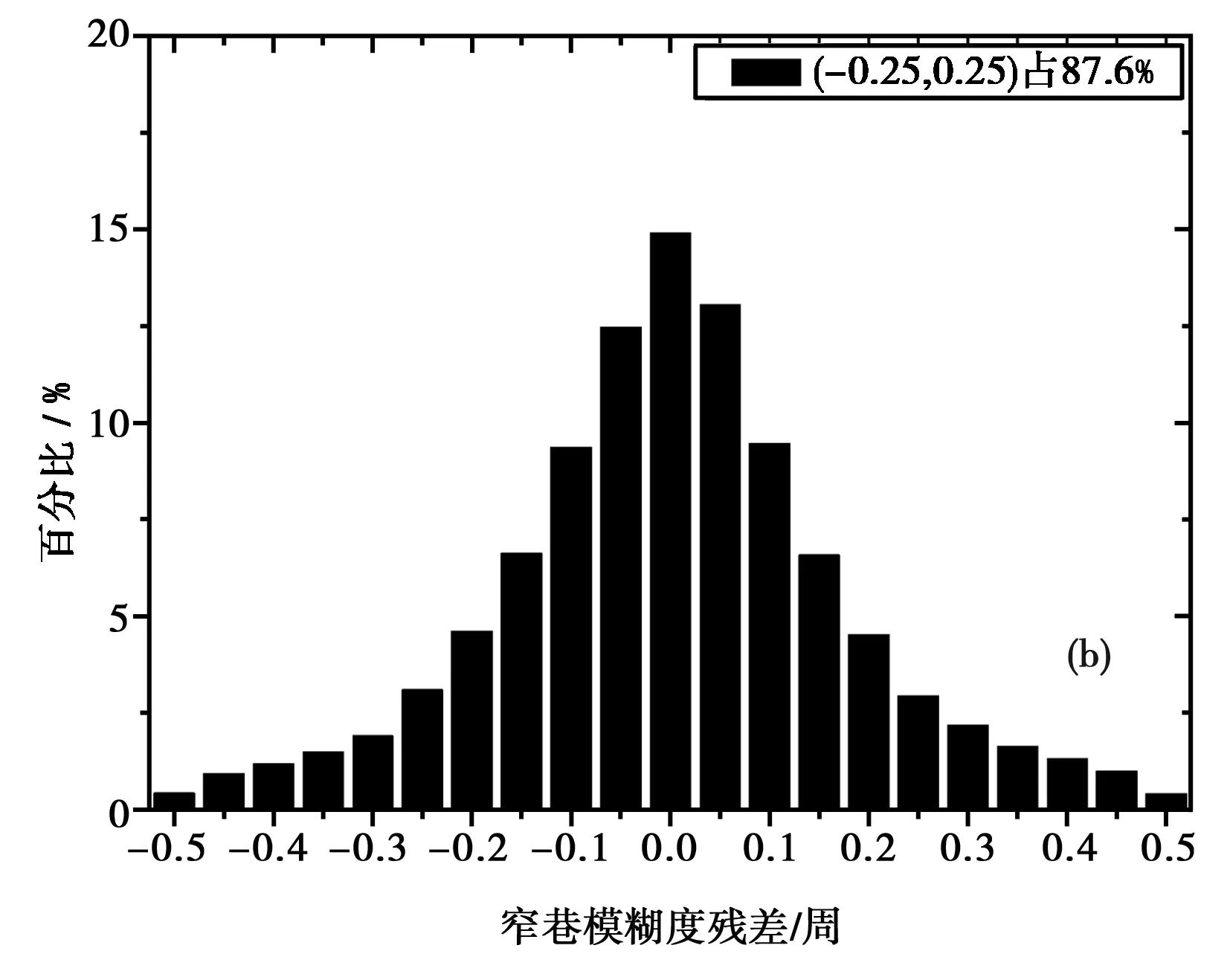
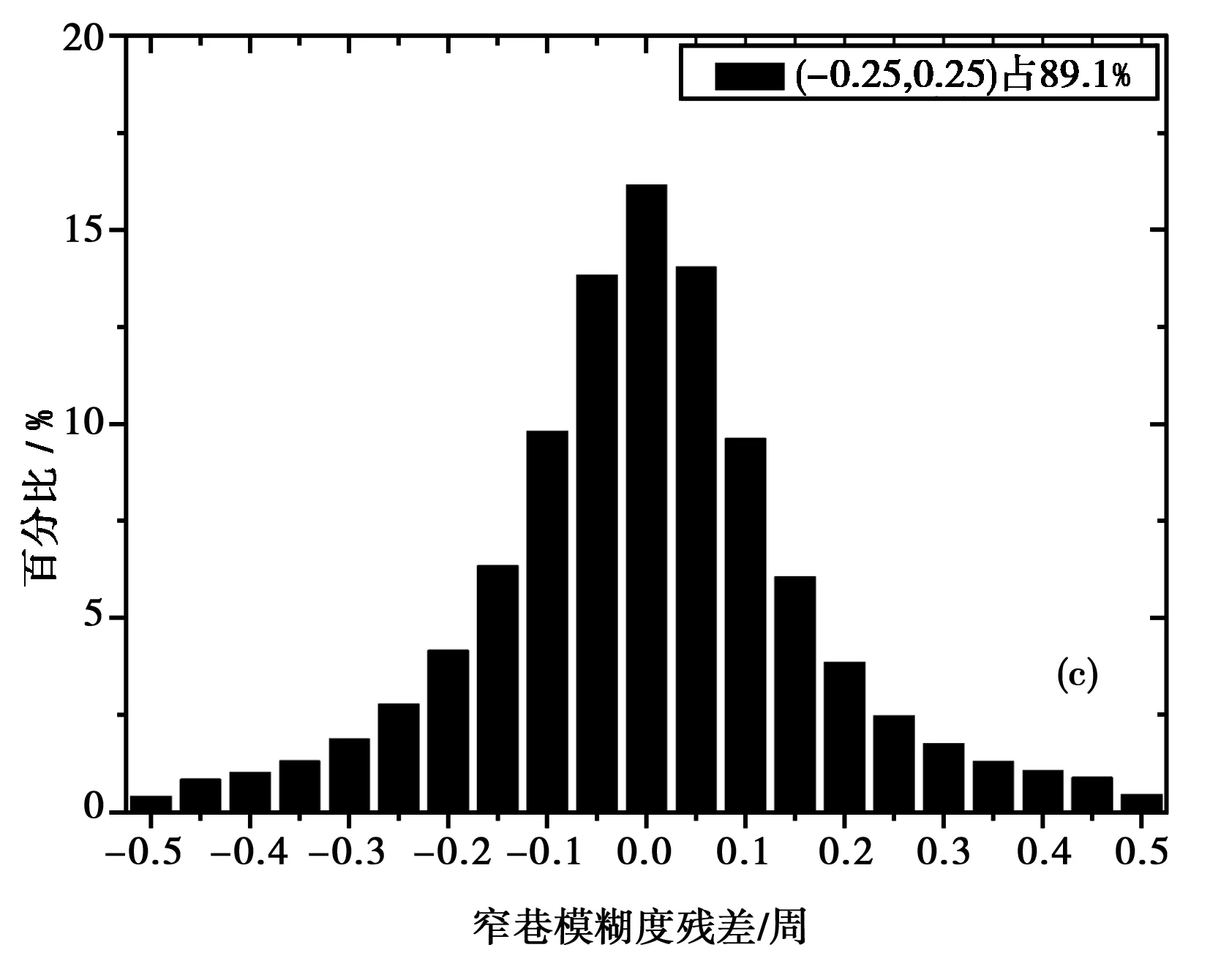
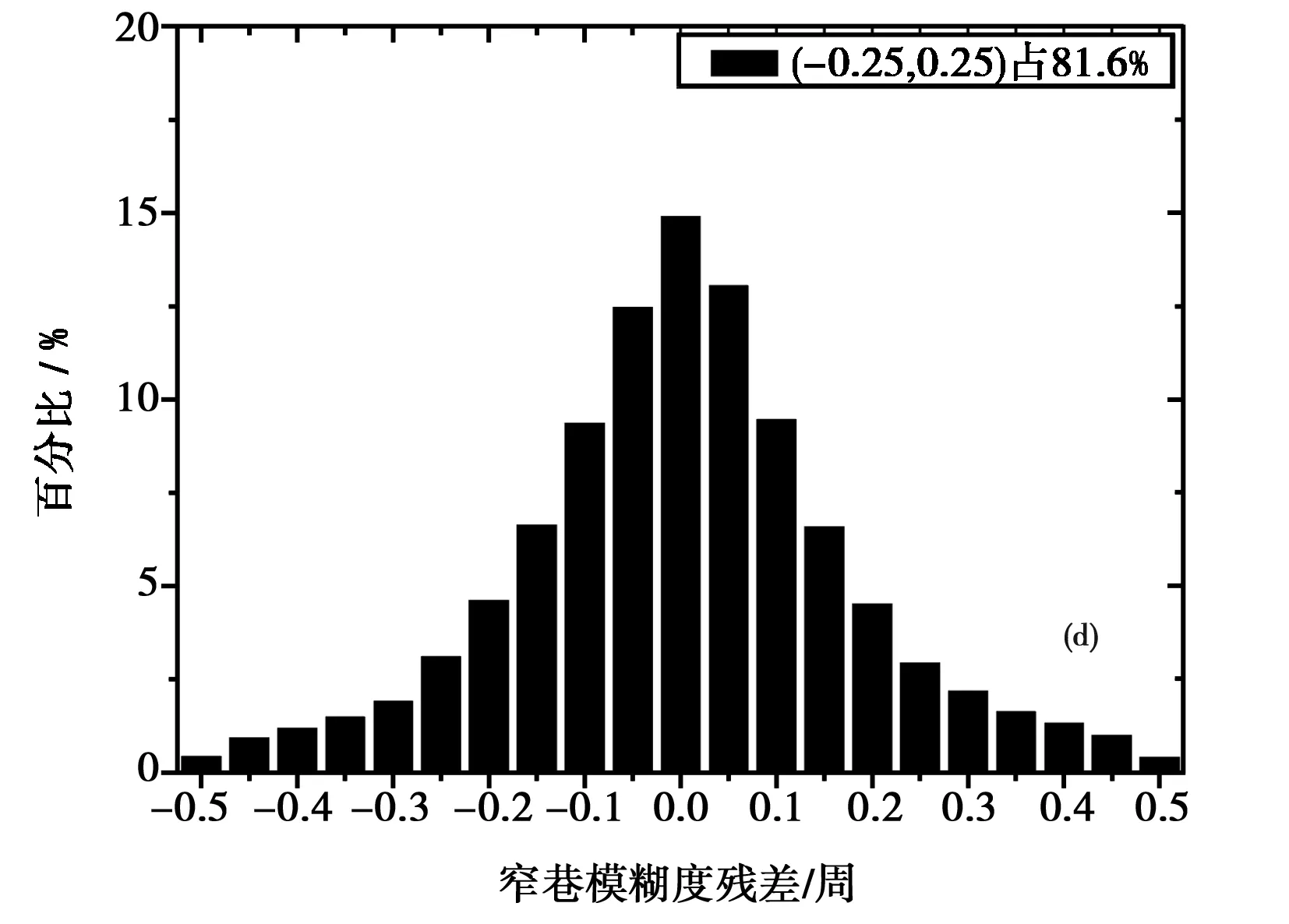
图5 选站数量不同宽巷模糊度残差的频率分布 (a) 40; (b) 80; (c) 230; (d) 312

当跟踪站较少时,会降低卫星对观测有效数据数,导致某些卫星对历元计算得到的窄巷FCBs不可靠。具体如图6,图7所示。

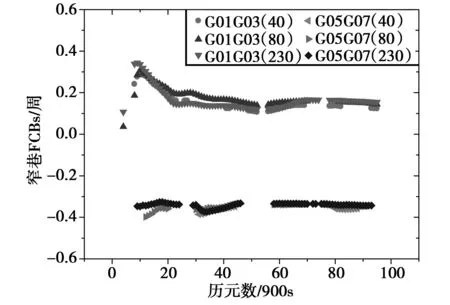
图6 部分卫星窄巷FCBs产品(至少5个跟踪站观测)

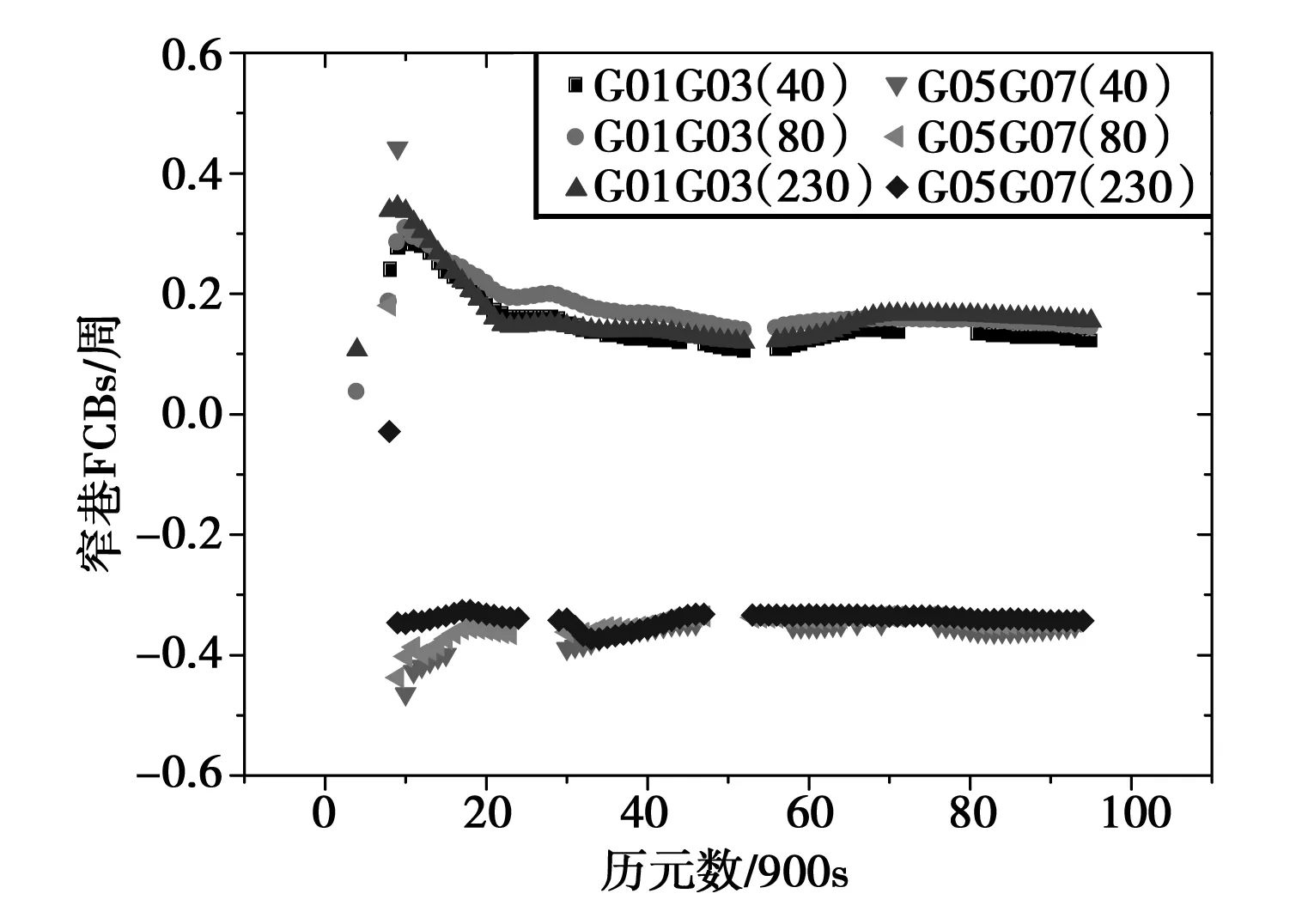
图7 部分卫星窄巷FCBs产品(至少3个跟踪站观测)

图6分别示出了卫星对G01G03和G05G07的窄巷FCBs的值,其中图6示出了至少5个跟踪站观测到该卫星对求得的历元窄巷FCBs值,图7给出了至少3个跟踪站观测到该卫星对求得的历元窄巷FCBs值。从上面两幅图中可知,三种方案窄巷FCBs的值符合程度较好,与方案3(230)的产品差值RMS统计值为0.05,表明,当跟踪站达到一定数量,就能保证FCBs产品的精度,增加站的数量对FCBs产品的质量提高较少。由于图中对方案1(40)、方案2(80)缺失历元个数被遮挡,不易观察,于是下面给出窄巷FCBs产品历元数百分比,以方案3(230)窄巷FCBs的总历元数为总集,产品窄巷FCBs历元数百分比为相应方案窄巷FCBs产品历元数与历元总个数的比值。对所有卫星对的窄巷FCBs进行统计。具体如表2所示。

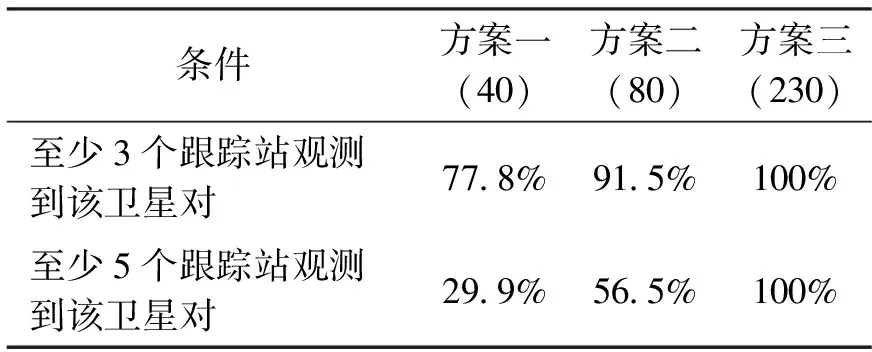
表2 所有卫星窄巷FCBs历元数百分比统计值

通过表2可以看出,随着站数量的减少,有效历元窄巷FCBs值逐渐减少,这将严重影响用户的使用,当方案1采用至少5个跟踪站观测到卫星对时,有效窄巷FCBs历元数仅为总历元数的29.9%,而方案2也只有56.5%,对于全球用户来说,大多数历元很可能没有相应的FCBs产品从而导致模糊度无法固定。当采用至少3个跟踪站观测卫星对时,与至少5个跟踪站观测到该卫星对相比,有较大改观,但从整体角度,仍不能选取40站全球跟踪站数量进行FCBs产品计算。因此上述方案仍需进一步改进。鉴于卫星对之间的相关性,于是对所有卫星对进行遍历,利用其它相关卫星对信息,增加该卫星对观测数据,从而解得该卫星对该历元下的窄巷FCBs产品。

如图7和表3所示,经过改进后,方案1(40)由原来的29.9%(5)、77.8%(3)提高到了90%(改进),括号中的数字分别代表不同策略。方案2(40)由原来的56.5%(5)、91.5%提高到99.6%。而数据的质量与前面为改进之前相比,变化不大,稳定性依然很好,表明改进方法有效,能够弥补由跟踪站少所带来的问题。而对于方案三(230)的窄巷FCBs历元更完整,分别提高22.2%(5)和5.3%(3)。

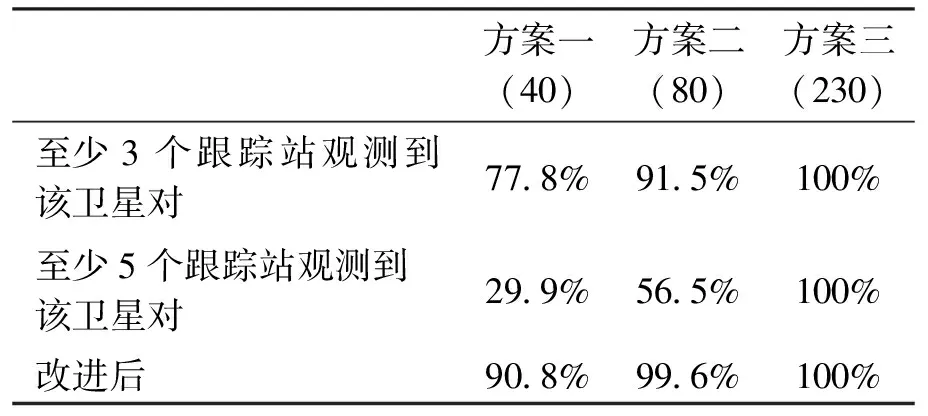
表3 改进前后所有卫星窄巷FCBs历元数百分比统计值

通过上述实验表明通过利用本文提出的选站策略选取40个站进行FCBs产品的计算可以达到选取230个站进行FCBs产品计算所获得的产品精度。在进行FCBs产品计算时,计算所需时间主要为计算窄巷FCBs时需要对所有参考站进行PPP浮点解解算,而选取40个站所需时间与PPP浮点解解算时间相比所需时间相对较短,仅相当4个站PPP浮点解解算时间,因此用上文提到的选站策略将显著减少计算FCBs产品所需的时间。

4 结束语

本文通过对用于PPP模糊度固定所用的FCBs产品的选战策略进行研究,提出了一套用于FCBs产品生成所需的选站策略。运用选站策略进行选站,结果表明通过提出的选站策略进行选站,选择有效的40个站所计算的FCBs产品的精度能够达到原有230个站所达到的计算的FCBs产品精度,证明了选站策略的有效性。

致谢:感谢信息工程大学iGMAS分析中心给予的帮助和支持。

[1] ZUMBERGE J F, HEFLIN M B, JEFFERSON D D,etal. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research: Solid Earth (1978—2012), 1997;102(B3):5005-5017.

[2] KOUBA J, HÉROUX P. Precise point positioning using IGS orbit and clock products[J]. GPS Solutions, 2001;5(2):12-28.

[3] 李征航,张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009.

[4] COLLINS P. Isolating and estimating undifferenced GPS integer ambiguities[C]//In Proceedings of ION National Technical Meeting, 2008:720-732.

[5] GE M, GENDT G, ROTHACHER M,etal. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008,82(7):389-399.

[6] LAURICHESSE D, MERCIER F, BERTHIAS J P,etal. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination[J]. Navigation, 2009，56(2):135-149.

[7] TEUNISSEN P J G. Success probability of integer GPS ambiguity rounding and bootstrapping[J]. Journal of Geodesy, 1998,72(10):606-612.

[8] DACH R, HUGENTOBLER U, FRIDEZ P,etal. Bernese GPS software version 5.2[D]. Astronomical Institute, University of Bern, 2015.

[9] HOFMANN-WELLENHOF B, LICHTENEGGER H, COLLINS J. Global positioning system: theory and practice[M]. Springer Science & Business Media, 2001.

[10]BLEWITT G. Carrier phase ambiguity resolution for the Global Positioning System applied to geodetic baselines up to 2000 km[J]. Journal of Geophysical Research, 1989,94(B8):10187-10203.

[11]GABOR M J, NEREM R S. GPS carrier phase ambiguity resolution using satellite-satellite single differences[C]//In Proceedings of the 12th international technical meeting of the satellite division of the institute of navigation,1999:1569-1578.

[12]DACH R, HUGENTOBLER U, FRIDEZ P,etal. Bernese GPS software version 5.0[D]. Astronomical Institute, University of Bern, 2007.

[13]DILSSNER F, SEEBER G, WÜBBENA G,etal, Impact of near-field effects on the GNSS position solution[C]//Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2008), 2001.

[14]GENDT G, DICK G, REIGBER C H,etal. Demonstration of NRT GPS water vapor monitoring for numerical weather prediction in Germany[J]. Journal Meteo Societ Jap, 2003,82(1B):360-370.

[15]李征航,黄劲松. GPS 测量与数据处理[M].武汉: 武汉大学出版社, 2010.

[16]魏勇. 基于TOPSIS的GNSS数据质量评估方法研究[R]. 2016.

[17]LI P, ZHANG X, REN X,etal. Generating GPS satellite fractional cycle bias for ambiguity-fixed precise point positioning[J]. GPS Solutions, 2015:1-12.

[18]党金涛. iGMAS精密定轨自动批处理策略及方法研究[D]. 郑州: 解放军信息工程大学, 2015.

Research on Station Selection Strategy of FCBs Products Used in PPP Ambiguitu Resolution

CHEN Xingyu,LI Jianwen,WEI Rongrong,GUO Liangliang

(SchoolofNavigationandAerospaceEngineering，InformationEngineeringUnivercity,Zhengzhou450052,China)

With the development of Precise Point Positioning (PPP), PPP has been gradually developed by the float resolution stage to ambiguity resolution stage. PPP Ambiguity Resolution (PPP-AR) has become the research focus. Moreover, FCBs product is the precondition of the PPP-AR. However, research on station selection strategy of FCBs products is not sufficient, based on the data quality assessment parameter of data integrity rate, wide-lane ambiguity residuals and integrated data quality of single satellite, this paper put forward a method, which used global grid method to select the tracking station. The results show that the accuracy of FCB product which used 40 station is equal to the accuracy of FCBs product which used 230 station and greatly reduce the time which are used in calculating the FCBs products.

PPP-AR; FCBs product; station selection strategy

10.13442/j.gnss.1008-9268.2016.05.002

2016-04-21

P228.4

A

1008-9268(2016)05-0005-08

陈星宇 (1989-),男,河北唐山人,硕士,现从事精密单点定位和完好性等方向研究。

李建文 (1971-),男,浙江富阳人,教授,现从事卫星导航系统工程与应用研究。

魏绒绒 (1991-),女,陕西咸阳人,硕士生,现从事卫星接收机相关研究工作。

郭亮亮 (1991-),男,山西吕梁人,硕士生,现从事卫星导航系统软件研制相关工作。

联系人： 陈星宇 E-mail: chenxingyu0201@163.com