长治市旅游线路的优化模型

郭伟，常金勇

（1.长治学院数学系，山西长治046011；2.中国科学院信息工程研究所，北京，100093）

长治市旅游线路的优化模型

郭伟1，常金勇2

（1.长治学院数学系，山西长治046011；2.中国科学院信息工程研究所，北京，100093）

为了研究如何选择最短旅游路径，在山西省长治市周边11个县中，各选取了1个具有代表性的旅游景点。通过分析，运用旅行售货商（TSP）模型，建立长治市旅游线路的优化模型，并借助LINGO工具编写程序，求出了一条最短路径。

旅游线路；优化模型；LINGO

1　引言

某位旅游爱好者打算在暑假期间到长治市各个县城的一些著名景点旅游。在山西省长治市周边的11个县中，各选取了1个具有代表性的旅游景点。他计划把长治市各个县城的最著名的景点旅游一遍，最后回到出发地，请问该游客应该选择怎样的旅游路线[1]，才能使他的总行程最短？

2　模型简介

求总行程最短可以利用旅行售货商（TSP）模型[2]来解决。我们首先查找景点位置，并计算任意两景点距离，最后建立模型并求解。

3　模型建立

3.1模型假设

1、在总行程最短的方案中我们不考虑堵车等情况；

2、绘制路线图时，把各景点的路线看做一个赋权的平面图[3]。

3、i：第i个景点，i=1，2，…，11

j：第j个景点，j=1，2，…，11

dij：第i个景点与第j个景点之间的距离

3.2模型的建立与求解

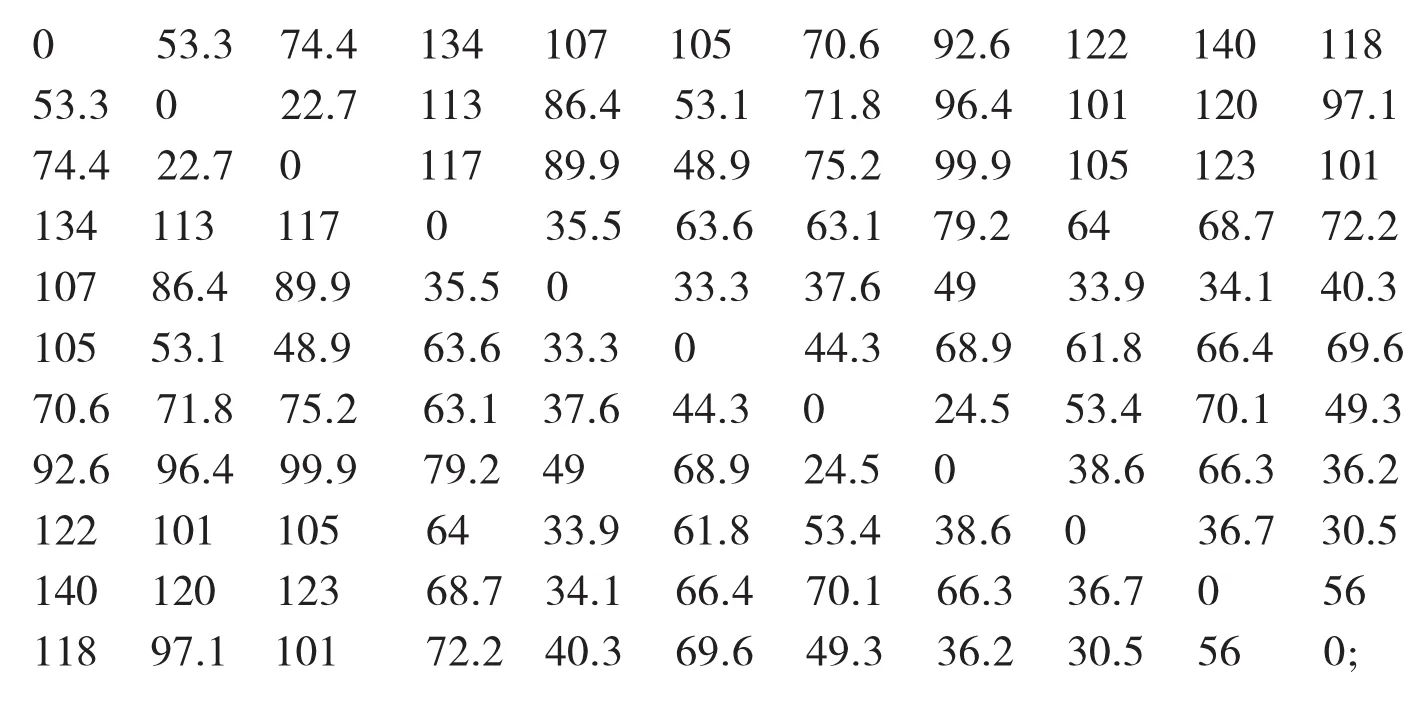
通过Google电子地图查出长治市旅游地图如图1所示﹙其中地图比例尺为1:1180000﹚。

不妨把长治市的旅游地图中各个县的著名景点进行处理，把地图上的每一条线路用线段表示，用顶点表示地图上的岔路口，即多条线段的交点，这样就形成了一个由点和线段组成的图。我们可以在每条线段上标上数字，表示两旅游景点之间的实际距离。在山西省长治市周边的各个县城所有景点中选择一个最具有代表性的著名景点，如表1所示。

表1　各个县城所选的著名旅游景点

记沁源县灵空山编号为1，其它景点依次编号为2、3、…、11，最后回到出发地，再重复时的编号为12。通过Google电子地图，查到各个景点的地理坐标（经度和纬度）如表2所示。

表2　各个著名旅游景点所在的地理位置

下面必须求出任意两个景点之间的实际距离。虽然地球不是一个标准的球体，但南北与东西长度相差不大，可以假设地球为一个球体，球体半径R=6371229公里。根据球面定理计算出东西方向的距离差为：

则可以计算出各个旅游景点之间的距离。

以点0表示出发点,称为原点，点1，2，…，n表示n个该游客需访问的景点。dij表示景点i到景点j的距离；xij=1表示该游客需要从景点i到景点j，因为该游客一定离开某一个景点去另一个景点，所以i≠j；xij=0表示不需要从景点i到景点j；ui表示旅游景点的顺序数。

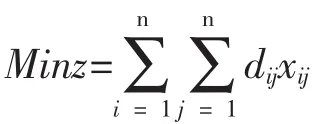
其中辅助条件ui（i=1，2，…，n）可以是连续变化的，显然这些变量在最优解中是普通的整数值。以总行程最短为原则，利用整数规划模型可求得各景点的旅行优先顺序。编写LINGO程序如下：

4　结果

只选取xij=1的结果，求得最优解为456.6公里，该游客的旅游路线如图2所示。

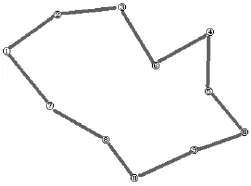
图2　旅游线路

显然这是一个循环圈，无论从哪个景点开始，顺序或逆序长治市旅游线路的总行程长度都是456.6公里。

［1］姜启源,谢金星,叶俊.数学模型［M］.北京:高等教育出版社,2003.80-90.

［2］甘应爱,田丰,李维铮.运筹学［M］.北京:清华大学出版社,2005.126-130.

［3］于东凯,刘玉树.基于平面图的最短路径算法的研究［J］.北京理工大学学报,2001，21（1）:31-34.

［4］谢金星,薛毅.优化模型与LINDO/LINGO软件［N］.北京:清华大学出版社,2005.124-186.

（责任编辑赵巨涛）

O224

A

1673-2014（2016）05-0026-03

山西省高校科技开发项目（2013158）；长治学院教学研究项目（JY201602）。

2016—07—13

郭伟（1982—），男，山西长治人，讲师，硕士，主要从事基础数学教学与研究。