关于实幂等矩阵性质的一些探讨
2016-12-20韩凯凯
韩凯凯
(长治学院数学系,山西长治046011)
关于实幂等矩阵性质的一些探讨
韩凯凯
(长治学院数学系,山西长治046011)
实矩阵从几何角度理解,可以看作欧氏空间到欧氏空间的线性变换。文章主要利用实矩阵的几何意义,给出了实幂等矩阵一些性质的不同证明,并给出了实对称幂等矩阵的一种刻画。
实幂等矩阵;特征值;特征子空间
1 引言
从几何角度理解,实矩阵可看作欧氏空间到欧氏空间的线性变换。文章主要利用实矩阵的几何意义,区别于[2]中的证明方法,给出了实幂等矩阵性质的不同证明。并给出了实对称幂等矩阵的一种刻画。
为了方便,文章在实数域R中讨论,记Mn(R)为实数域R上的全体n阶矩阵组成的集合,记:
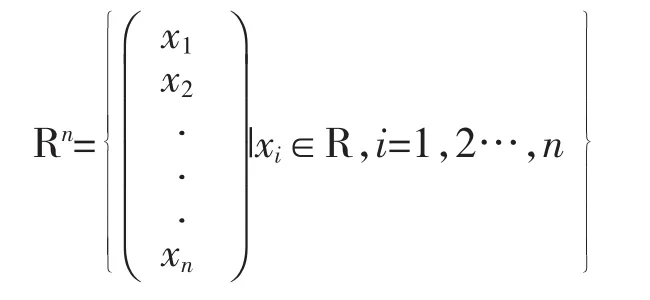
2 预备知识
定义1设A∈Mn(R),若A=A2,则称A为实幂等矩阵。若A=A'=A2,则称A为实对称幂等矩阵。
引理1设A=(α1,α2,…αn)∈Mn(R),αi是A的第i列组成的列向量(i=1,2,…,n),则:
(1)Ran(A)=L(α1,α2,…αn);(Ran(A)表示A的值域);
(2)rank(A)=dimRan(A);
(4)Ran(A)的一组基的原象与Ker(A)的一组基构成Rn的一组基,并且rank(A)+dimKer(A)=n。
证明参看[1]。
引理2【1】对于任意一个n级实对称矩阵A,都存在一个n级正交矩阵T,使T'AT=T-1AT成对角形。
证明参看[1]。
引理3【2】设A∈Mn(R),则A为幂等矩阵(实对称幂等矩阵)当且仅当En-A为幂等矩阵(实对称幂等矩阵)。
证明由定义直接可得。
3 主要定理
定理1【2】设A为n级实幂等矩阵,则:
(1)A可对角化,并且A的特征值皆为0或1;
(2)A的特征值1的重数=rank(A),A的特征值0的重数=n-rank(A);
(3)A的属于1的特征子空间为L(α1,α2,…αn),其中A=(α1,α2,…αn);A的属于0的特征子空间为Ker(A);
(4)rank(A)=tr(A);
(5)rank(A)+rank(En-A)=n;反之,若满足rank(A)+rank(En-A)=n,则A为实幂等矩阵。
证明:
(1)设A=(α1,α2,…αn),因为A2=A,故Aαi=αi(i=1,2,…,n)。设rank(A)=r,不妨设α1,α2,…αr线性无关,设βr+1,…,βn为Ker(A)的一组基。由引理1(4)知,α1,α2,…αr,βr+1,…,βn为Rn的一组基,且A在该组基下的矩阵为对角矩阵,对角线元素只有0和1,故A可对角化,并且A的特征值皆为0或1。
(2)因为A可对角化,且对角线元素只有0和1,故1的重数=rank(A),0的重数=n-rank(A)。
(3)因为αi(i=1,2,…n)均属于A的特征子空间V1,故L(α1,α2,…αn)哿V1。由(2)知,dimL(α1,α2,…αn)=dimV1,于是V1=L(α1,α2,…αn)。显然,A的属于0的特征子空间为Ker(A)。
(4)由(1)知,A可对角化,且对角线元素均为0和1,于是rank(A)=tr(A)。
(5)若A为n级实幂等矩阵,rank(A)=rank(En-A)=tr(En-A)=tr(A+En-A)=tr(En)=n。
若A满足rank(A)=rank(En-A)=n,由引理1知,rank(A)+dimKer(A)=n,故rank(En-A)=dimKer(A)=Ker(A)。下证:Ran(En-A)=Ker(A)。坌ξ∈Ker(A),因为Aξ=0,故(En-A)ξ=ξ-Aξ=ξ,于是ξ∈Ran(En-A),Ker(A)哿Ran(En-A)。
因为dimRan(En-A)=rank(En-A)=dimKer(A),于是Ran(En-A)=Ker(A)。
因为Ran(En-A)=Ker(A),坌x∈Rn,(En-A)x∈Ker(A),于是A(En-A)x=0,Ax=A2x,故A2=A。
推论1设A为n级实幂等矩阵,则:
(1)En-A的特征值皆为0或1,且1的重数=n-rank(A),0的重数=rank(A);
(2)En-A的属于1的特征子空间为Ker(A);En-A的属于0的特征子空间为Ran(A)=L(α1,α2,…αn),其中A=(α1,α2,…αn)。
证明:(1)A为n级实幂等矩阵,由引理3知,En-A为实幂等矩阵。由定理1知,En-A的特征值皆为0或1,1的重数为rank(En-A)=tr(En-A)=tr(En)-tr(A)=n-rank(A)。于是0的重数为rank(A)。
(2)显然可证:En-A的属于1的特征子空间即为A的属于0的特征子空间。En-A的属于0的特征子空间即为A的属于1的特征子空间。
推论2设A为n级实对称幂等矩阵,则:
(1)存在正交矩阵T使得T-1AT=diag{1,1…,1,0,…0};
(2)A的属于1的特征子空间L(α1,α2,…αn)与A的属于0的特征子空间Ker(A)互为正交补,于是Rn=L(α1,α2,…αn)⊕Ker(A)。(⊕正交和符号);
(3)A是半正定矩阵。
证明:
(1)由引理2和定理1可证;
(2)由于A=A',由引理1可证;
(3)由(1)知,存在正交矩阵T使得T'AT= T-1AT=diag{1,1…,1,0,…0}。故A是半正定矩阵。
下面给出实对称幂等矩阵的一种刻画。
定理2【2】设X是数域R上n×k矩阵,rank(X)=k,令B=X(X'X)-1X',则:
(1)B是n级实对称幂等矩阵;
(2)rank(B)=k;
(3)B有特征值1(重数为k)和0(重数为n-k);
(4)B的属于特征值1的特征子空间为l1Xe1+…lkXek=L(Xe1,…,Xek),ej表示第j个分量为1、其余分量为0的单位列向量,lj∈R(j=1,2,…,n)。B的属于特征值0的特征子空间为L(Xe1,…,Xek)⊥。
证明:(1)
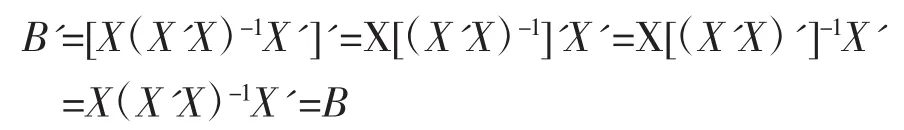
B2=X(X'X)-1X'X(X'X)-1X'=X(X'X)-1X'=B,故B是实对称幂等矩阵。
(2)rank(B)=Tr(B)=Tr(X(X'X)-1X')=Tr(X'X(X'X)-1)=Tr(Ek)=k。
(3)由定理1可证。
(4)
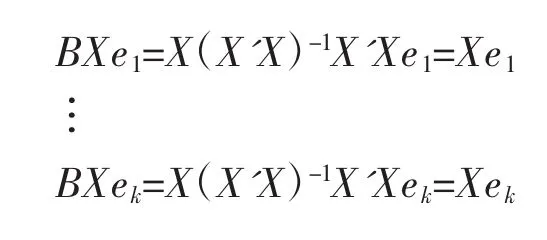
因为rank(X)=k,则Xe1,…,Xek线性无关,故Xe1,…,Xek是B的属于特征值1的特征向量。因为B可对角化,B的属于特征值1的特征子空间的维数等于特征值1的重数=k,故B的属于特征值1的特征子空间为L(Xe1,…,Xek)⊥。
由推论2(2)知,B的属于特征值0的特征子空间为L(Xe1,…,Xek)⊥。
定理3设B是n级实对称幂等矩阵,rank(B)=k,B的属于特征值1的特征子空间为L(β1,β2,…βk),记X=(β1,β2,…βk),则B=X(X'X)-1X'。
证明:令C=X(X'X)-1X',由定理2知,C是n级实对称幂等矩阵,rank(C)=k,C的属于特征值1的特征子空间为L(β1,β2,…βk),C的属于特征值0的特征子空间为L(β1,…βk)⊥。由推论2知,B的属于特征值0的特征子空间为L(β1,…βk)⊥。于是坌ξ∈Rn,设ξ=ξ1+ξ2(ξ1∈L(β1,…βk)⊥,ξ2∈L(β1,…βk)⊥)(正交和),Bξ=B(ξ1+ξ2)=ξ1=C(ξ1+ξ2)=Cξ,于是B=C。
[1]丘维声.高等代数.[M]北京:高等教育出版社,1996.
[2]邱森,朱林生.高等代数探究性课题精编[M].武汉:武汉大学出版社,2012,100-109.
(责任编辑赵巨涛)
Research on Some Properties of Real Idempotent Matrices
Han Kai-kai
(Maths Department of Changzhi University,Changzhi Shanxi 046011)
From the view of geometry,real matrices may be seen as linear transformations on Euclidean spaces.According to the geometric meaning,we give different proofs for some properties of real idempotent matrices,and give a description of the real symmetrical idempotent matrices.
real idempotent matrices;eigenvalue;eigen-subspace
O151.2
A
1673-2014(2016)05-0001-03
2016—06—21
韩凯凯(1986—),男,河北邢台人,硕士,助教,主要从事泛函分析研究。
