基于响应面法的磁力齿轮参数优化设计

周晓刚，辛灿祥

(1.苏州健雄职业技术学院，苏州 215400；2.上海电力学院，上海 200090)



基于响应面法的磁力齿轮参数优化设计

周晓刚1，辛灿祥2

(1.苏州健雄职业技术学院，苏州 215400；2.上海电力学院，上海 200090)

为优化磁力齿轮的设计参数，建立磁力齿轮的有限元计算模型，分别探究各个设计参数对磁力齿轮输出转矩的影响；采用DOE实验设计方法，对各个设计参数对磁力齿轮转矩的重要性进行量化；利用响应面法得到设计参数与最大输出转矩的数学模型，并预测出最优的设计参数组合。对二维有限元模型的计算，验证了预测结果的正确性。

磁力齿轮；实验设计；响应面法；最优参数组合

0 引 言

随着稀土永磁材料性能的提升，磁力齿轮开始引起学者们的关注。基于磁场调制原理的磁力齿轮因具有高转矩密度脱颖而出。它规避了传统机械齿轮的拓扑结构，在传统磁力齿轮的基础上引入调磁铁块，使磁力齿轮的永磁体得到充分利用，继而提高了磁力齿轮的最大转矩和转矩密度。现有磁力齿轮的转矩密度可与机械齿轮相媲美，同时避免了机械齿轮接触摩擦、噪音大、振动剧烈和维护困难等缺点，使得磁力齿轮的工业应用具备了广泛的现实基础[1-6]。

磁力齿轮的拓扑结构在学者的研究中不断扩展，关于磁力齿轮设计参数的选择及其影响的研究则相对较少。目前关于磁力齿轮优化的研究对象主要包括调磁铁块厚度、内外气隙的大小、内外转子轭部的厚度和永磁体的厚度等变量。文献关注的对象是单一变量变化对齿轮最大静态转矩大小的影响，忽略了多个变量之间的相互影响，导致所得到的关于磁力齿轮结构参数的设计和优化方面的结论并不准确和全面[7-11]。

本文针对磁力齿轮结构参数多、参数选择难度大等问题，建立磁力齿轮有限元计算模型，在分别研究单个设计参数对最大转矩影响的基础上，结合实验设计方法和响应面全局优化算法，对磁力齿轮的结构参数进行综合优化。

1 设计参数与最大输出转矩

最大转矩的大小是衡量磁力齿轮性能最重要的指标。磁力齿轮设计参数的选择对最大转矩的大小有着重要的影响。文献[1]中分析发现，在传动比为特定小数时，磁力齿轮的转矩脉动可限制在5%以内。因此，本文选择传动比为3∶22的磁力齿轮为研究对象，后续关于设计参数的选择均建立在此基础之上。

1.1 永磁体厚度

图1 输出转矩与永磁体厚度的关系

1.2 调磁铁块的高度和宽度

定义调磁块宽度比w=s1/s2，其中s1表示调磁块外径对应的圆弧长度，s2表示空隙部分外圆弧长度，且s=s1+s2。定义调磁铁块高度比R=h/s，其中，h表示调磁铁块的径向高度。调整调磁铁块高度和宽度，对气隙磁密做谐波分析，发现高度和宽度的变化均会导致气隙磁密的变化，对应次调制谐波的磁密幅值存在差异，进而影响最大转矩的幅值。在调磁铁块宽度取一定值时，最大输出转矩随调磁铁块厚度的变化如图2所示。显然，在调磁铁块高度取某值时，对应的输出转矩出现极大值。图3展示了宽度的变化对外气隙磁密的影响。图3中22次谐波幅值的大小直接决定了输出转矩的大小。由图2和图3可知，调磁铁块的高度和宽度对磁力齿轮的输出转矩有很大影响。

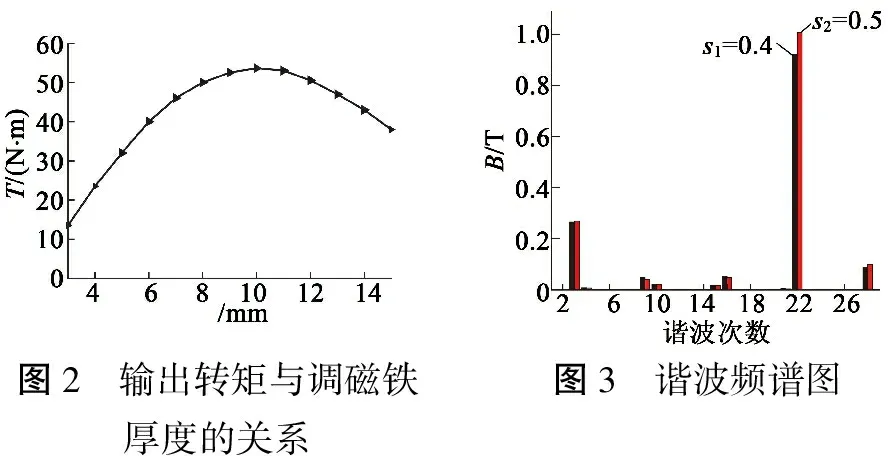
图2 输出转矩与调磁铁厚度的关系图3 谐波频谱图

1.3 内外气隙长度

内外气隙的大小影响磁力线在内气隙、调磁块和外气隙中的路径，进而影响调磁块的调磁性能。所以，内外气隙大小的取舍也是优化中需要考虑的问题。如图4所示，输入转矩和输出转矩与内气隙的大小呈负相关。内气隙长度越大，内外转子永磁体之间的耦合程度降低，相互作用力也减弱。

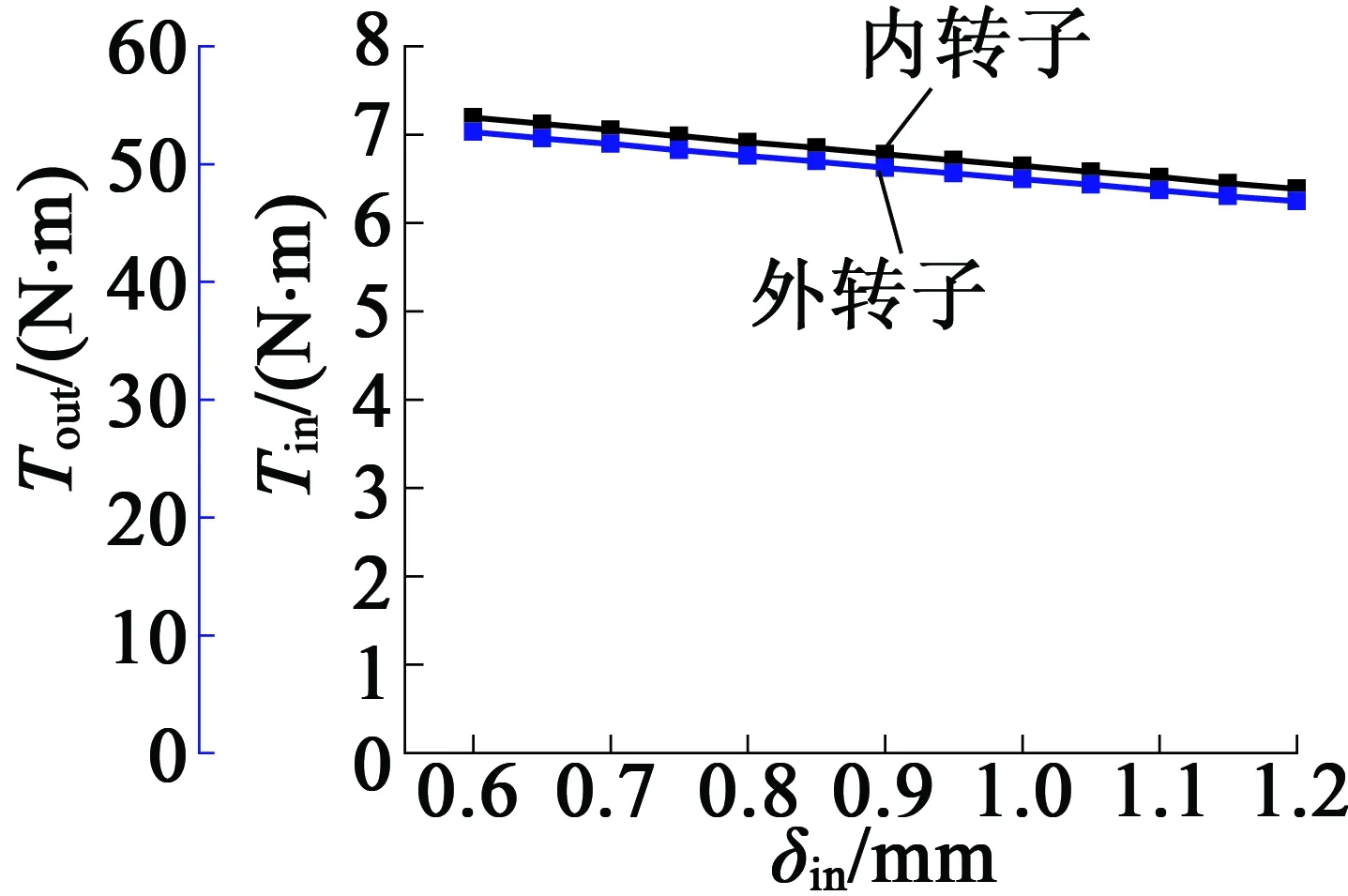
图4 转矩与内气隙长度的关系

2 实验设计与综合优化

2.1 响应面法

响应面是指响应变量η与一组输入变量(ζ1,ζ2,ζ3,…，ζk)之间的函数关系式：η=f=(ζ1,ζ2,ζ3,…，ζk)。响应面法(以下简称RSM)通过大量的测量数据建立一个数学模型，然后通过数学模型得到最优条件和最佳目标响应。其数学模型可表示：

(1)

式中：a是通过拟合大量实验数据得到的常系数，X表示相关的独立变量，Y表示目标响应。

在磁力齿轮的优化问题中，选取磁力齿轮的输出转矩T为目标响应，约束变量分别为内转子永磁体厚度X1、内气隙长度X2、调磁铁块高度X3和宽度X4、外气隙长度X5和外转子永磁体厚度X6。

2.2 综合优化

本文建立磁力齿轮有限元模型的约束条件如表1所示。将正交表应用于实验设计得到46组实验数据，所得数据依据响应面法拟合得到表2；其中，R2表示实验结果与实际结果的相关性，且R2≤1；AdjR2是R2的校正系数，AdjR2≤1。R2越接近于1，说明设计实验所得结果越接近真实值。AdjR2的值越接近于1，说明所讨论的设计参数具有统计学意义，所得数学模型能很好地揭示响应与设计参数的之间的关系。显然表2的结果表明本文所得数学模型与真实模型的拟合度很好。

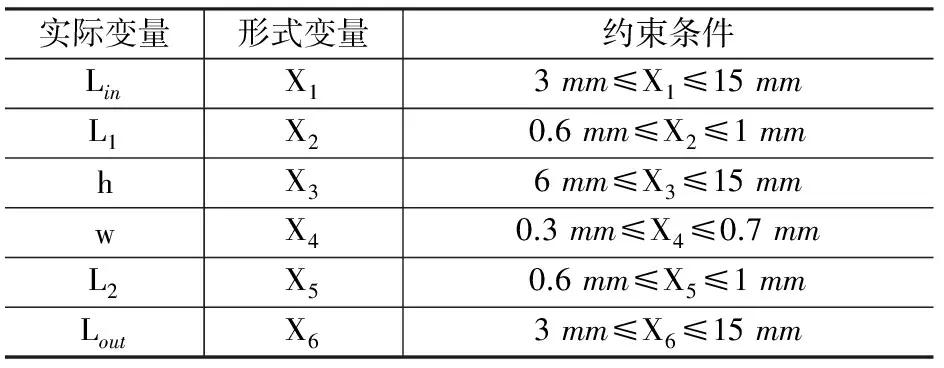
表1 设计参数的约束条件

表2 实验设计结果

目标响应最大输出转矩与变量之间的数学关系可表示：

T=64.73+20.89X1-0.37X2+2.76X3+8.80X4-1.04X5+6.69X6-0.03X1X2+

1.91X1X3+2.04X1X4-0.37X1X5-

3.03X1X6-0.17X2X3+0.23X2X4+0.02X2X5+0.01X2X6-0.15X3X4-0.07X3X5+0.97X3X6+0.22X4X5+

(2)

通过该数学模型，可以得到最优参数组合如表3所示。经计算发现，优化后的设计参数可以在很大程度上提高磁力齿轮的最大输出转矩，其增幅高达32%。且优化后的磁力齿轮体积更小，其转矩密度增幅更大。

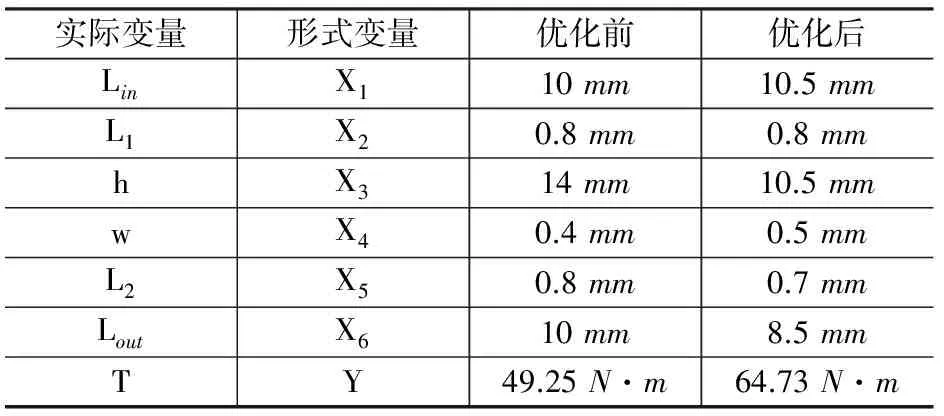
表3 优化前后结果对比

3 结 语

本文首先基于有限元方法对永磁体厚度，调磁铁块的高度、宽度和内外气隙的大小等设计参数进行分析和计算；在此基础上，基于实验设计方法，对多个设计参数进行组合优化，得到如下结论：

(1)要获得更大输出转矩，内转子永磁体的厚度要比外转子永磁体厚度大；

(2)随对调磁铁块高度的变化，最大输出转矩会出现极大值；

(3)调磁铁块宽度的变化，会影响漏磁的变化，进而使得特定次气隙磁密的幅值存在差异，进而造成输出转矩的不同；

(4)实验设计方法可以很好的应用于磁力齿轮设计参数的组合优化，并为多变量的参数优化提供了一种新的方法。

[1] 杜世勤，章跃进，江建中.新型永磁复合电机研究[J].微特电机，2010，38(4):1-3.

[2] 宁文飞，包广清，李树豹，等.磁场调制式同心齿轮的结构优化和参数分析[J].磁性材料及器件，2013(1):21-23.

[3] 王双全.永磁磁性齿轮的研究现状及发展前景[J].科技创新导报，2012(18):12.

[4] 王虎生， 侯云鹏， 程树康.无接触磁力齿轮传动机构发展综述[J].电工技术学报，2008(2):72-73．

[5] 宁文飞，包广清，王金荣.磁齿轮拓扑分析及其应用综述[J].机械传动，2012，36(2):91-96.

[6] 杜世勤.磁场调制式磁力齿轮及其有限元计算[J].上海电机学院学报, 2011，14(3): 173-177.

[7] 刘细平，易靓，刁艳美，等.磁齿轮传动永磁同步风力发电机分析[J].微特电机，2013，41 (7): 34-37.

[8] 包广清，刘新华，毛开富.基于磁场调制式磁齿轮传动的永磁同步风力发电系统[J].农业机械学报，2011，42(5):116-120.

[9] 彭科容，邢敬娓，李勇，等. 一种基于磁导调制原理的新型磁力齿轮的原理与试验研究[J].微特电机, 2011，39(1):29-31.

[10] 杜世勤，江建中，章跃进，等.一种磁性齿轮传动装置[J].电工技术学报，2010，25(9):41-46.

[11] 刘新华.新型磁场调制式磁性齿轮的设计研究[D].上海：上海大学，2008.

Optimization Design of Magnetic Gear's Parameters Based on Response Surface Method

ZHOU Xiao-gang1，XIN Can-xiang2

(1.Suzhou Chien-Shiung Institute of Technology,Suzhou 215400, China；2.Shanghai University of Electric Power,Shanghai 200090,China)

In order to optimize the design parameters of the magnetic gear, the finite element model of the magnetic gear was established and the influence of various design parameters on output torque of magnetic gears was explored respectively. This paper quantified the importance of each magnetic gear's design parameter by applying DOE experimental design method. The mathematical model of maximum output torque and design parameters was obtained by the response surface method. This paper also predicted the optimal design parameter combination through the mathematical model. The calculation of two-dimensional finite element model verifies the accuracy of the predicted results.

magnetic gear; experimental design; response surface methods; optimal parameter combination

2016-02-19

TM351

A

1004-7018(2016)10-0041-03

周晓刚(1976-)，男，硕士，副教授，研究方向为机械制造工艺。