进口防旋板对孔型密封非定常气流激振特性的影响

李志刚,李军,2,丰镇平

(1.西安交通大学能源与动力工程学院,710049,西安;2.先进航空发动机协同创新中心,100191,北京)



进口防旋板对孔型密封非定常气流激振特性的影响

李志刚1,李军1,2,丰镇平1

(1.西安交通大学能源与动力工程学院,710049,西安;2.先进航空发动机协同创新中心,100191,北京)

为了展示透平机械密封系统设计中进口防旋板在改善密封转子动力特性和增强转子系统稳定性的止旋方面的性能,采用基于转子多频椭圆轨迹涡动模型和动网格技术的非定常数值方法,研究了进口防旋板对孔型密封非定常气流激振力和转子动力特性系数的影响,计算分析了进口预旋比分别为0和0.6时2种进口防旋板结构的孔型密封转子动力特性系数、非定常气流激振力和流场特性,并与实验结果进行了对比。研究表明:非定常数值方法能够准确预测与频率相关的孔型密封转子动力特性系数;进口预旋可显著减小孔型密封的有效阻尼、增大有效阻尼项的穿越频率,易诱发转子涡动失稳;进口防旋板能够有效减小孔型密封的进口旋流速度、孔型密封的交叉刚度和有效阻尼穿越频率,增大孔型密封的有效刚度和有效阻尼,进而提高转子系统的稳定性。

孔型密封;进口预旋;防旋板;气流激振;转子动力特性

透平机械旋转动密封在控制泄漏流动的同时,还会产生流体激振力,影响转子的稳定性[1]。目前透平机械主要通过采用先进阻尼密封结构(蜂窝密封、孔型密封和袋型密封)、调整动静间隙、安装止旋装置(分流注射器和防旋板)等,来抑制和解决密封气流激振力引起的转子失稳问题[2-3]。安装在密封进口的一系列与密封面成一定角度的导流板,能够阻滞和引导密封进口的周向旋流。

迷宫密封进口周向旋流速度对密封交叉刚度具有决定性的作用,而气流激振力是诱发转子失稳的主要因素。Benckert等通过实验证明了在迷宫密封进口安装防旋板结构能够减小密封交叉刚度[4-5],而Childs等研究表明防旋板对直接刚度和直接阻尼影响很小且实验测量了迷宫密封在无防旋板、直角防旋板和反旋流角防旋板3种情况下的转子动力特性系数[5-6]。Nielson等发现反旋流角防旋板结构并没有比直角结构表现出更优的性能[7]。图1给出了迷宫密封进口直角防旋板和反旋流角防旋板结构[7]。

工程应用中单独采用防旋板结构改善来流条件或采用阻尼密封代替迷宫密封的方法往往达不到完全消除转子失稳的目的。Scharrer报道了采用蜂窝密封代替迷宫密封无法完全消除航天飞机高压氧涡轮泵转子的亚同步涡动,但通过在蜂窝密封上游安装防旋板达到了此目的[8],Zeidan等也是通过采用带进口防旋板的蜂窝密封使多级离心压气机的转子非同步涡动降低到了安全水平[9]。Childs等研究表明,减小密封进口正预旋或增大负预旋能够显著提高孔型密封的有效阻尼,增强转子系统的稳定性[10-11]。

(a)直角防旋板 (b)反旋流角防旋板图1 迷宫密封进口防旋板结构

针对旋转阻尼密封转子动力特性计算,晏鑫等提出了双控制体Bulk Flow模型的方法和基于单频涡动模型的非定常计算流体动力学(CFD)方法[12-13],李志刚等提出了基于多频单向和椭圆涡动模型的非定常CFD方法[14-15]。

本文采用基于多频椭圆轨迹涡动模型和动网格技术的非定常CFD方法,计算了2种进口预旋和防旋板结构下的孔型密封转子动力特性系数、非定常气流激振力和流场,分析了进口预旋和防旋板对孔型密封非定常气流激振特性的影响,以期为阻尼密封防旋板的设计提供理论基础和技术数据。

1 计算模型和数值方法

1.1 计算模型

图2给出了孔型密封的几何结构[10]。表1给出了孔型密封的几何参数和实验工况[10]。本文选取了2种进口预旋比u0(u0=0,0.6)并定义了密封进口的流动方向。u0为密封进口气体周向旋流速度与转子面线速度的比值,即

(1)

式中:Uθ为密封进口周向旋流速度;n为转子转速。式(1)可表征密封进口旋流速度的大小。根据图1所示的2种迷宫密封进口防旋板结构,本文设计了2种孔型密封进口防旋板结构,如图3所示,其由周向等弧度排列的36个导流片组成,且具有与密封相同的径向间隙。

图2 孔型密封实验件几何结构

图4给出了孔型密封和防旋板的三维计算模型和网格。孔型密封、进口防旋板的计算模型和网格均为360°整周全三维结构。采用ANSYS ICEM CFD软件生成多块结构化网格,每个密封孔和防旋板导流片为O型网格,壁面区域采用加密网格,在密封间隙处沿径向布置了20个节点。根据文献[15]网格无关性分析,当网格节点数达到519万时,本文计算可获得网格无关解。因此,计算孔型密封的网格节点数为592万,直角防旋板和反旋流角防旋板结构的网格节点数分别为248万和297万。

表1 孔型密封实验件几何参数和实验工况[10]

(a)直角防旋板

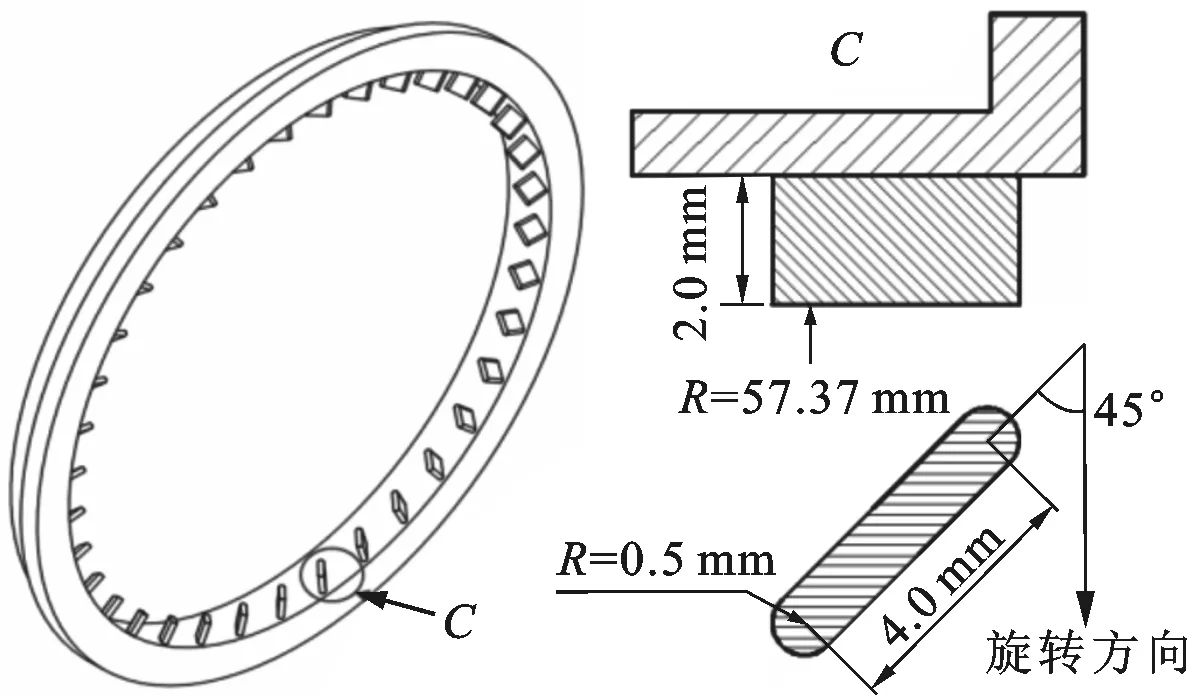
(b)反旋流角防旋板图3 2种进口防旋板几何结构

图4 孔型密封、进口防旋板计算模型和网格

1.2 数值方法

本文采用基于多频椭圆轨迹涡动模型和动网格技术的非定常数值方法、采用ANSYS-CFX数值求解的Unsteady Reynolds-Averaged Navier-Stokes(URANS)方程,计算了孔型密封的非定常流场和流体激振力。图5给出了转子椭圆轨迹涡动模型。表2给出了具体的数值方法和涡动模型参数。多频椭圆轨迹涡动模型中的转子涡动位移的数学表达式如下。

x方向激励

(2)

y方向激励

(3)

式中:a和b分别为椭圆轨迹的长轴和短轴;N为涡动频率数;Ω0=2πf0为涡动基准频率,f0为涡动频率。

(a)x方向激励 (b)y方向激励图5 转子椭圆轨迹涡动模型示意图

表2 数值方法和涡动模型参数

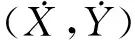
(4)

对于x方向激励和y方向激励,在对2种转子涡动位移下的密封流场进行独立的非定常求解后,通过快速傅里叶变换(FFT)可获得式(4)在频率内的表达式,即

(5)

式中:Hij=Kij+iωCij为密封阻抗系数。通过非定常CFD数值求解和FFT变换可获得频率内的密封流体激振力Fij和转子涡动位移Dij,进而通过式(5)获得密封转子动力特性系数。本文非定常数值方法、多频转子椭圆轨迹涡动模型和转子动力特性系数提取方法的详细介绍和验证可参考文献[14-15]。

2 结果分析与讨论

2.1 转子动力特性系数

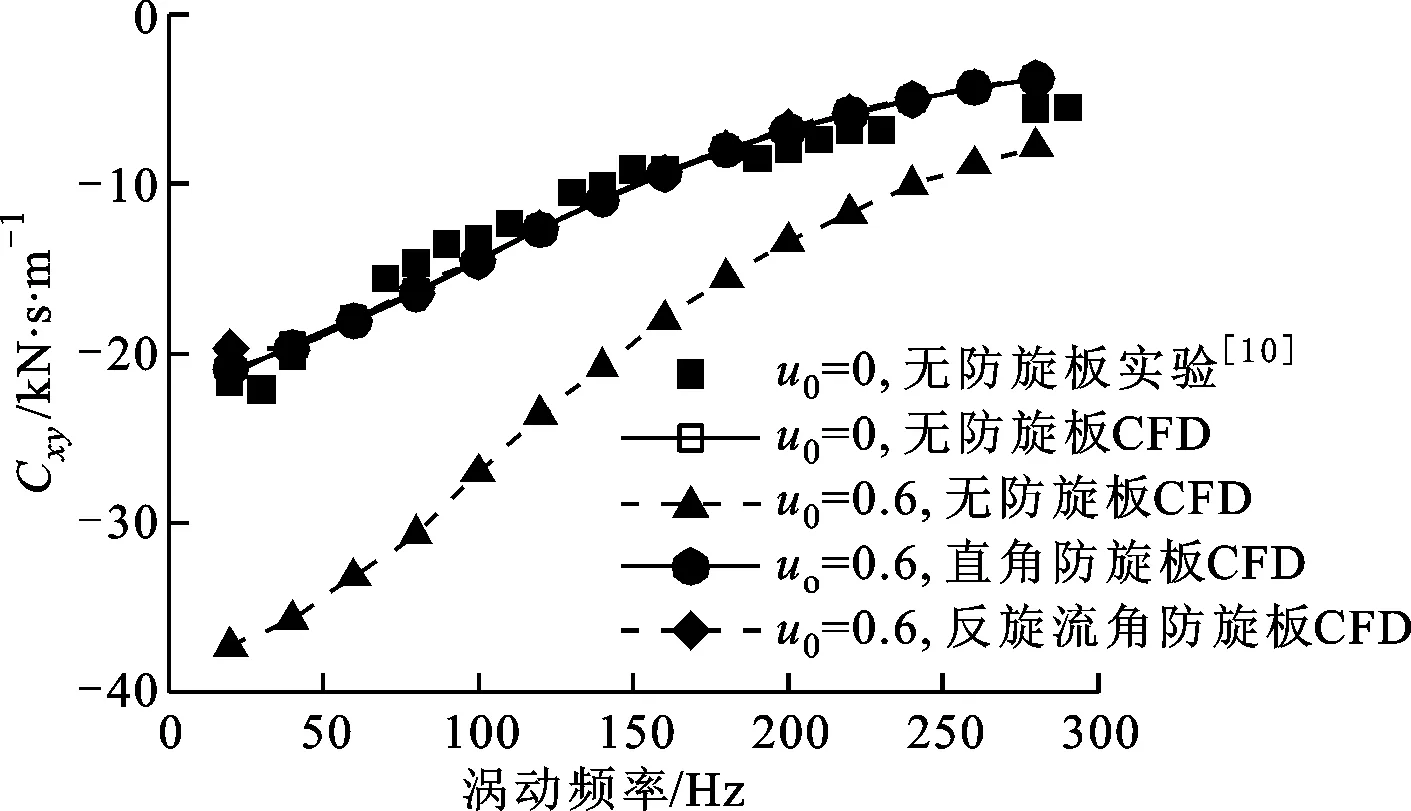
图6给出了在2种进口预旋和防旋板结构下,孔型密封转子动力特性系数随涡动频率的变化。本文引入有效刚度系数Keff和有效阻尼系数Ceff来评价孔型密封的转子动力特性,即

Keff=Kxx+CxyΩ

(6)

Ceff=Cxx+Kxy/Ω

(7)

为验证数值方法的准确性,对进口无预旋(u0=0)、无进口防旋板时孔型密封的转子动力特性系数进行了计算,并与实验结果进行了比较。如图6所示,除直接阻尼和有效阻尼在80～280Hz范围内略微偏小外(偏差小于20%),其余数值结果与实验值吻合良好,表明本文的非定常数值方法能够准确分析孔型密封的转子动力特性系数。

(a)直接刚度

(b)直接阻尼

(c)交叉刚度

(d)交叉阻尼

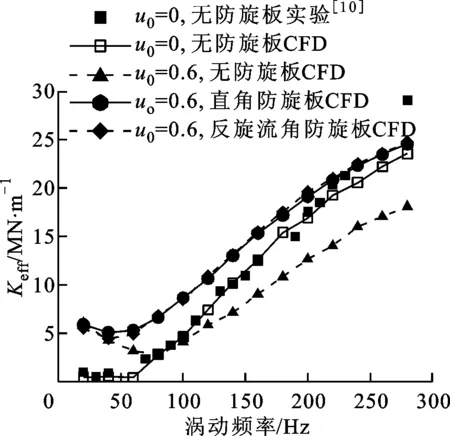
(e)有效刚度

(f)有效阻尼图6 孔型密封转子动力特性系数随涡动频率的变化

如图6所示:进口预旋会使孔型密封的直接刚度和交叉刚度增大,但使直接阻尼和交叉阻尼减小;相比于直接动力系数,进口预旋会显著影响交叉动力系数;在80～280 Hz范围内,进口预旋会使有效刚度减小、有效阻尼显著减小、穿越频率显著增大。可见,进口预旋不但会减小转子系统稳定运行的频率范围(密封有效阻尼为正的频率范围)、引起转子失稳,还会降低转子系统的一阶临界转速。因此,工程中应采取措施来减小密封进口预旋。

图6还显示:进口防旋板对孔型密封的直接刚度和直接阻尼影响较小,但使交叉刚度显著减小、交叉阻尼显著增大;进口防旋板使孔型密封的有效刚度和有效阻尼均显著增大,有效阻尼项的穿越频率显著减小;2种进口防旋板结构下的孔型密封具有几乎相同的转子动力特性系数。因此,采用进口防旋板能够有效抑制转子系统的振动,消除密封进口预旋引起的转子失稳问题,其中直角防旋板和反旋流角防旋板对孔型密封转子动力特性具有同等的改善效果。

2.2 非定常气流激振力和流场

图7给出了进口预旋比u0=0.6时不同进口防旋板下孔型密封作用于转子面上的非定常气流激振力的变化。如图7所示,进口防旋板能有效减小孔型密封的非定常气流激振力。

(a)x方向气流激振力

(b)y方向气流激振力图7 孔型密封内非定常气流激振力(u0=0.6,x方向激励)

进口防旋板之所以能够改变密封的非定常气流激振特性,是因为其改变了密封进口流体的流动参数,特别是进口旋流速度。表3给出了不同进口防旋板下密封处的流动参数。进口防旋板使密封处的旋流速度显著减小,使泄漏量略微增大(小于4.5%),对静压和轴向速度影响很小。

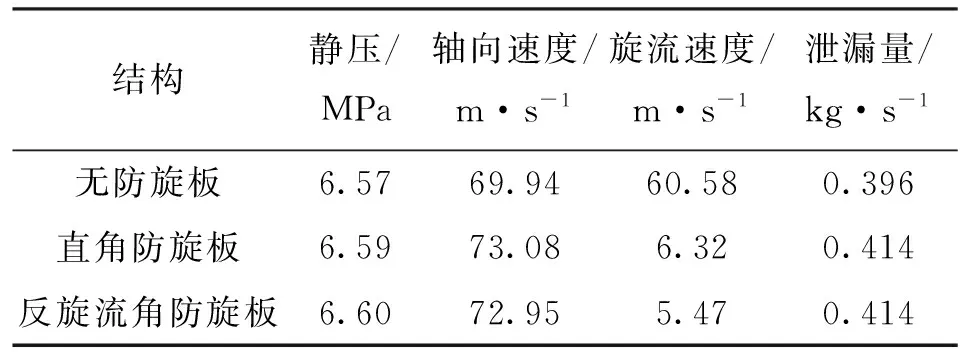
表3 密封处的流动参数(u0=0.6)

图8给出了密封通道内平均旋流速度沿轴向的分布。图9给出了3种防旋板下防旋板通道内的三维流场。相比于无进口防旋板情况,2种防旋板结构均能有效阻断流体的周向流动,减小流体的周向速度。受转子面的黏性剪切作用和孔型静子面的阻滞耗散作用,防旋板的止旋效果仅在密封上游区域有效。2种防旋板结构止旋效果相近,反旋流角防旋板结构并未达到有效控制流体的流动方向、使流动反向旋转的目的。这主要是相邻导流片间的弧度间隔太大、流体未发生有效偏转的缘故。因此,工程中需要对导流板的结构参数(导流片数目、安装角度、轴向长度等)进行优化,使其能够有效控制流体的流动方向。

图8 密封通道内平均旋流速度沿轴向的分布(u0=0.6)

(a)无防旋板 (b)直角防旋板

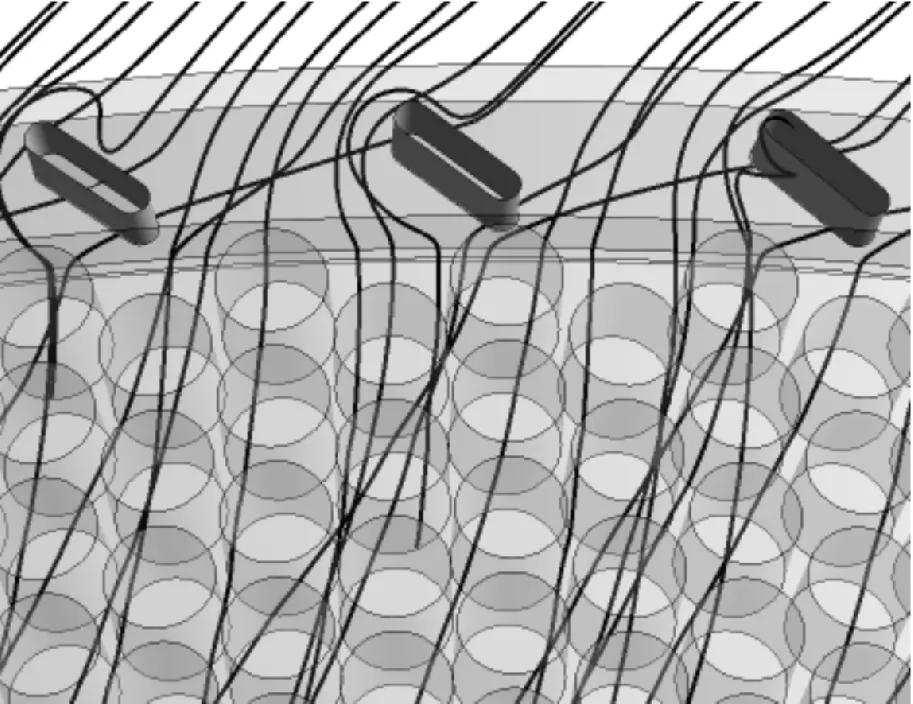
(c)反旋流角防旋板图9 防旋板通道内的三维流场(u0=0.6)

3 结 论

本文采用基于多频椭圆轨迹涡动模型的非定常CFD方法,研究了进口预旋、进口导流板对孔型密封非定常气流激振特性的影响。

进口预旋会使孔型密封交叉动力系数的绝对值显著增大、密封有效刚度和有效阻尼显著减小、有效阻尼项的穿越频率明显增大;进口预旋不但会减小转子系统稳定运行的频率范围、引起转子失稳,同时还会降低转子系统的一阶临界转速。

进口防旋板能够有效阻断密封进口流体的周向流动、减小密封进口旋流速度,进而减小密封交叉刚度、增大有效刚度和有效阻尼、减小有效阻尼项的穿越频率。直角防旋板和反旋流角防旋板对孔型密封转子动力特性具有同等的改善效果,因此在密封进口处安装防旋板是一种提高转子系统阻尼、消除转子涡动失稳的有效措施。

[1] VANCE J M. Machinery vibration and rotordynamics [M]. New York, USA: John Wiley & Sons, 2010: 271-272.

[2] CHILDS D W, VANCE J M. Annular seals as tools to control rotor dynamic response of future gas turbine engines, AIAA 94-2804 [R]. Reston, VA, USA: AIAA, 1994.

[3] LI J, CHOUDHURY P D, KUSHNER F. Evaluation of centrifugal compressor stability margin and investigation of antiswirl mechanism [C]∥Proceeding of the 32nd Turbomachinery Symposium. Texas, USA: Texas A&M University, 2003: 49-57.

[4] BENCKERT H, WACHTER J. Flow induced spring coefficients of labyrinth seals for application in rotordynamics [C]∥Proceedings of a Workshop on Rotordynamic Instability Problems in High-Performance Turbomachinery. Texas, USA: Texas A&M University, 1980: 189-212.

[5] CHILDS D W, RAMSEY C. Seal rotordynamic coefficient test results for a model SSME ATD-HPFTP turbine interstage seal with and without a swirl brake [J]. ASME Journal of Tribology, 1991, 113(1): 198-203.

[6] CHILDS D W, MCLEAN J E, ZHANG M, et al. Rotordynamic performance of a negative-swirl brake for a tooth-on-stator labyrinth seal, GT2014-25577 [R]. New York, USA: ASME, 2014.

[7] NIELSON K K, CHILDS D W, MYLLERUP C M. Experimental and theoretical comparison of two swirl brake designs [J]. ASME Journal of Turbomachinery, 2001, 123(2): 353-358.

[8] SCHARRER J. Test results for leakage and rotordynamic coefficients;comparisons to labyrinth and smooth configurations [J]. ASME Journal of Triboloby, 1989, 111(2): 300-301.

[9] ZEIDAN F Y, PEREZ R X, STEPHENSON E M. The use of honeycomb seals in stabilizing two centrifugal compressors [C]∥Proceedings of 22nd Turbomachinery Symposium, Turbomachinery Laboratory. Texas, USA: Texas A&M University, 1993: 3-15.

[10]CHILDS D W, WADE J. Rotordynamic-coefficient and leakage characteristics for hole-pattern-stator annular gas seals-measurements versus predictions [J]. ASME Journal of Tribology, 2004, 126(2): 326-333.

[11]BROWN P, CHILDS D. Measurement versus predictions of rotordynamic coefficients of a hole-pattern gas seal with negative preswirl [J]. ASME Journal of Engineering for Gas Turbines and Power, 2012, 134(12): 122503.

[12]晏鑫, 李军, 丰镇平. BULK FLOW方法分析孔型密封转子动力特性的有效性 [J]. 西安交通大学学报, 2009, 43(1): 24-28. YAN Xin, LI Jun, FENG Zhenping. Validation of two-control-volume BULK FLOW method for rotordynamic characteristics of hole-pattern seals [J]. Journal of Xi’an Jiaotong University, 2009, 43(1): 24-28.

[13]YAN X, LI J, FENG Z. Investigations on the rotordynamic characteristics of a hole-pattern seal using transient CFD and periodic circular orbit model [J]. ASME Journal of Vibration and Acoustics, 2011, 133(4): 041007.

[14]李志刚, 李军, 丰镇平. 袋型阻尼密封转子动力特性的多频单向涡动预测模型 [J]. 西安交通大学学报, 2012, 46(5): 13-18. LI Zhigang, LI Jun, FENG Zhenping. Multiple frequencies one-dimensional prediction model of rotordynamic characteristics for pocket damper seals [J]. Journal of Xi’an Jiaotong University, 2012, 46(5): 13-18.

[15]LI Zhigang, LI Jun, YAN Xin. Multiple frequencies elliptical whirling orbit model and transient RANS solution approach to rotordynamic coefficients of annual gas seals prediction [J]. ASME Journal of Vibration and Acoustics, 2013, 135(3): 031005.

(编辑 苗凌)

Effect of Swirl Brakes on Unsteady Flow Excitation Characteristics of Hole-Pattern Seal

LI Zhigang1,LI Jun1,2,FENG Zhenping1

(1. School of Energy & Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. Collaborative Innovation Center of Advanced Aero-Engine, Beijing 100191, China)

To reveal the anti-swirl performance of the swirl brake on improving the seal rotordynamic performance and enhancing rotor stability in turbomachinery, the effects of swirl brakes on the transient flow excitation characteristics and rotordynamic coefficients of a hole-pattern seal are numerically investigated. With computational fluid dynamics (CFD) method based on the multi-frequency elliptical orbit rotor whirling model and mesh deformation technique, the rotordynamic coefficients, transient fluid response forces and flow pattern of the hole-pattern seal are solved and analyzed for two types of swirl brakes at inlet preswirl ratios of 0 and 0.6. The predicted rotordynamic coefficients are compared with the experiment data. The numerical results show that the present transient numerical method enables to accurately predict the frequency-dependent rotordynamic coefficients of hole-pattern seal. Inlet preswirl significantly decreases effective damping in the hole-pattern seal and increases in the crossover frequency of the effective damping term, which usually induces rotor instability vibration. The swirl brake is very useful to eliminate rotor instability vibration because it can obviously reduce the cross-coupling stiffness and the crossover frequency, and increase the hole-pattern seal effective stiffness and effective damping by reducing the inlet preswirl velocity.

hole-pattern seal; inlet preswirl; swirl brake; flow excitation; rotor dynamic

2015-03-30。 作者简介:李志刚(1986—),男,讲师。 基金项目:国家自然科学基金资助项目(51406144);博士后科学基金资助项目(2014M550490)。

时间:2015-10-23

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151023.1106.012.html

10.7652/xjtuxb201601003

TK474

A

0253-987X(2016)01-0016-06