一种新的类别型数据聚类算法

赖芨宇，陈克明

(1.福建农林大学 交通与土木工程学院，福州 350002；2.东华大学 管理学院，上海 200051)

一种新的类别型数据聚类算法

赖芨宇1，陈克明2

(1.福建农林大学 交通与土木工程学院，福州 350002；2.东华大学 管理学院，上海 200051)

文章基于类别数据集合引入质量和特征向量的概念；确定了计算类别型数据的相似度；给出聚类结果清晰度及其变化率的定义；提出一种对质量和特征向量有效聚类类别型数据的算法。

类别型数据；聚类；质量；特征向量；清晰度

0 引言

数据挖掘中聚类算法的应用很广泛。在商务上，聚类能帮助市场分析人员从客户基本库中发现不同的客户群，并且用不同的购买模式来刻画不同的消费群体的特征。在生物学上，聚类能用于帮助推导植物和动物的种类、基因和蛋白质的分类，获得对种群中固定结构的认识。聚类在地球观测数据中相似地区的确定，根据房屋的类型、价值和位置对一个城市中房屋的分类发挥作用。聚类也能用来对web上的文档进行分类，以发现有用的信息。聚类分析能作为一种独立的工具来获得数据分布的情况，观察每个簇的特点，并对某些特定的节点进一步分析。此外，聚类还可以作为其他方法的预处理步骤。聚类的目标是使同一类对象的相似度尽可能地小；不同类对象之间的相似度尽可能地大。目前聚类的方法有很多种。与数值型数据相比，类别型数据的聚类研究成果相对较少，其有效性也值得进一步探讨。

对于类别型数据，本文提出一种基于质量和特征向量的聚类算法。首先，初始集合被划分为含有相同数据对象的初始类，后续工作基于这些初始类展开。其次，借助于万有引力定律的理念，将质量和特征向量概念引入到这些类中，使用层次聚类算法对其聚类，并采用清晰度概念确定合理聚类个数，最后实验数据验证算法的有效性。

1 特征向量和距离

本文提出质量和特征向量概念，进一步地定义了类别型数据之间距离。

1.1 特征向量

假设D={X1， X2， …， Xn}是含有n个类别型数据，带有p个属性(A1，A2，…，Ap)的集合。这里,Ai是第i个属性的取值集合{ai1，ai2，…，aiqi}，其中，i=1,2,…,p。

设该集合没有任何的先验信息，且各个属性的权重都是一样的，每个属性取值之间是均等的。类别型数据的属性取值表示如下：

（责任编辑/易永生）

进一步地，构造一个q维向量，q=q1+q2+…+qp，如下：N=(n11，n12，…，n1q1，n21，n22，…，n2q2，…，np1，np2，…，npqp)这里，nimi是集合D中属性aimi出现的次数之和，其中i=1,2,...,p;m=1,2,...,qi。

分割集合D为M个初始的非空集合(D1，D2，…，DM)，称为单元。每个单元含有的元素的取值是相同的，单元Dk含有nk个元素(k =1，2，…，M )，且n1+n2+…+nM=n。这里单元可以看作集合D的初始聚类结果，下面的聚类分析就是从这些单元开始的。

假设单元 Dk中元素取值为a1k1，a2k2，…，apkp，这里kl∈{1 ，2,...,ql},l=1，2,...,p。这样可以构造对应予单元Dk的一个向量，表示如下：

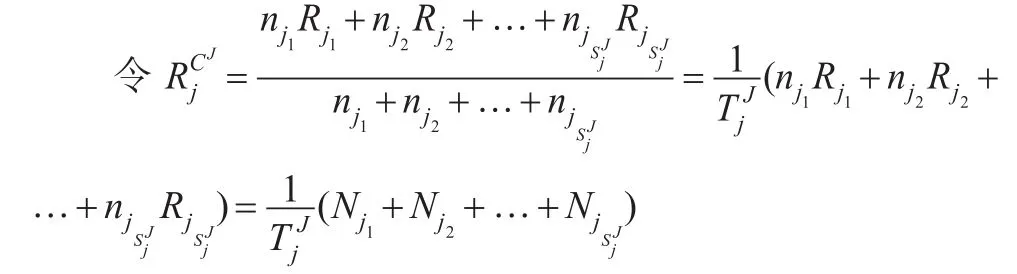
1.2 类别型数据之间的距离

利用单元的特征向量和质量的定义，以万有引力法则，定义两个单元之间的距离为：

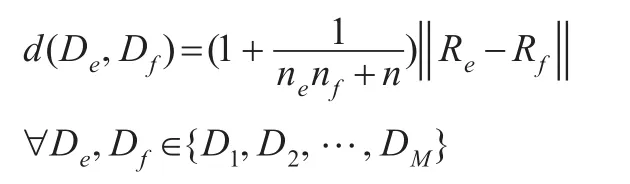
同样地，两个子类间的距离定义为：

为了避免“黑洞现象”（如果一个子类的质量与其他子类的质量相差较大时，那么在随后的聚类过程中，质量较小的类会被质量较大的类一个一个地吞噬掉，以上类似于宇宙中的“黑洞现象”），引入参数和到距离公式中。这两个参数主要用来降低质量对单元或子类间距离的影响，数值实验表明这两个参数的引入是非常有效的。

2 确定聚类个数

一般地，聚类个数越多，类内元素越相似，聚类结果越清楚。因此，本文提出一个计算聚类清晰度的算法。清晰度是衡量特定聚类的整体特征的量。如果把原始集合看作一个聚类结果，则其清晰度最低；如果把每个元素看作一个子类，则清晰度最高。

定义聚类结果(C1J,C2J,…,CJJ)(1≤J≤M))的清晰度计算如下：

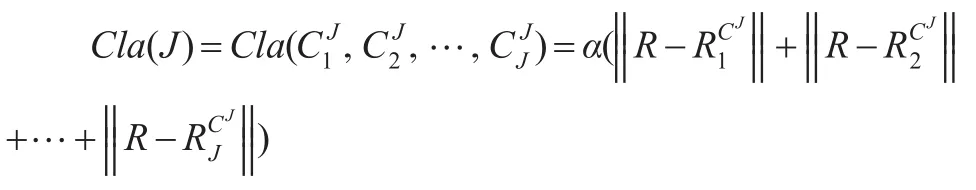
再采用凝聚式的层次聚类算法，聚类个数单调地由M变为1时，那么聚类结果的清晰度就单调地由1变为0。

比较Cla(3)和Cla(4)：

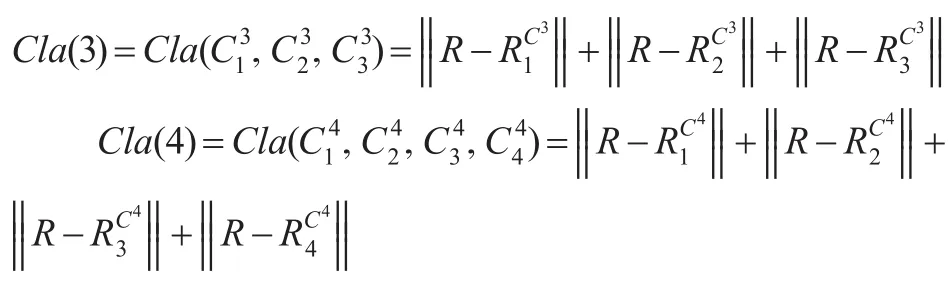
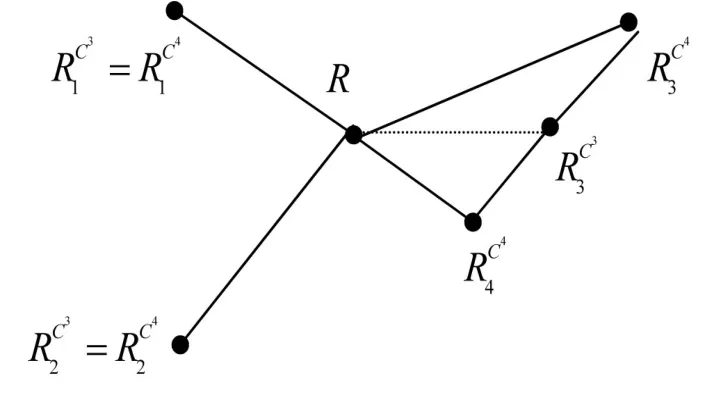
图1 Cla(4)到Cla(3)的清晰度

聚类清晰度(Cla(J))显示了当数据集合被划分为J个子类时聚类结果的整体特征。随着聚类个数的增加，清晰度也在增加。为了得到合理的子类个数，可以计算聚类结果清晰度的变化率，定义如下：

数列Δ2，Δ3，…，ΔM-1出现最小值时，相邻聚类个数的聚类结果的清晰度变化相对最小。根据清晰度变化率的定义，如果Δi(2≤i≤M-1)是最小值，那么数字i就是合理的聚类个数。在实践中，数列的第一个极小值所对应的聚类个数通常确定为合理聚类个数。

3 实验

本文选取三个数据集合进行验证。它们分别是投票数据集合、乳癌数据集合和动物园数据集合，均来自于机器学习资料库。

3.1 投票数据集合

投票数据集合是美国国会的一次投票数据，包含435个样本，每个样本有16个属性，且每个属性取值集合均为{Y,N,U}。投票数据集合分为两组，一组是民主党议员，另一组是共和党议员，详细内容请见http://www.sgi.com/ tech/mlc/db/vote.all。

根据特征向量的定义，该集合的单元或子类的特征向量是48（16*3）维的。利用1.2节对类别型数据之间距离定义，本文采用凝聚式层次聚类算法得到一组数列，如表1所示。

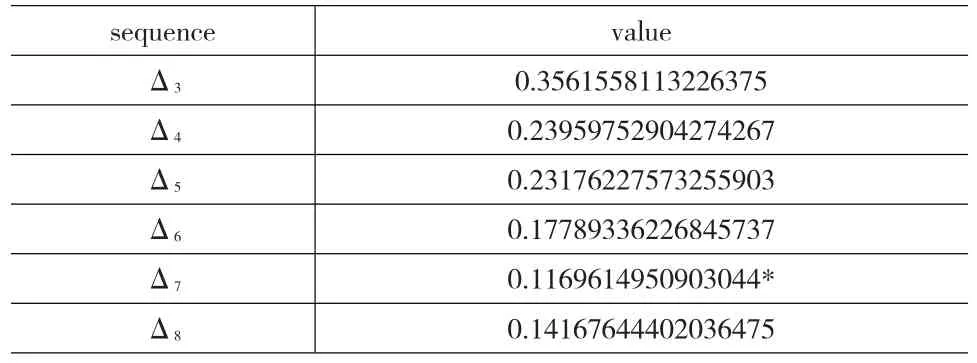
表1 投票数列集合的数列变化率

由于Δ7是数列(Δ3,Δ4,…,Δ8)的极小值（实际上，Δ7也是第一个局部极小值），那么合理的聚类个数定为7。

当聚类个数为7时，获得聚类结果如表2所示。

表2 投票数据集合的聚类结果

表2是投票数据集合的聚类结果。聚类结果由2个非常大的子类和5个很小的子类组成。5个很小的子类仅包含8个数据元素，它们依次是68,168,253;30;154;257,262; 289。在聚类过程中，本文把435个数据对象按照原始顺序标记为0～434。也就是说，68号元素也就是原始数据集合的第69个元素。分析表明这8个元素与其他元素相差很大。也就是说，这8个元素可以看作该集合的离群点元素。

在cluster-1中有205个数据元素，其中158个是共和党人，47个是民主党人。cluster-1的部分元素属于共和党人，也就是说，77.1%(158/205)的元素被正确地聚类到共和党一组中。

在cluster-2中有222个数据元素，其中215个是民主党人，仅有7个是共和党人。也就是说，高达96.8%(215/ 222)的元素被正确地聚类到民主党一组中。

3.2 乳癌数据集合

乳癌数据集合取自http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/，共包含699个样本。样本数据含有9个属性，每个属性的取值集合均是{1,2,…,10}。每个样本要么是属于良性组，要么是属于恶性组。另外，由于这699个元素中有16个元素含有缺失值，因此本实验的数据对象是不包含缺失值的685个元素。

类似地，可以得到该集合不同聚类结果清晰度变化率的数列Δ3,Δ4,…,Δ11，见表3所示。

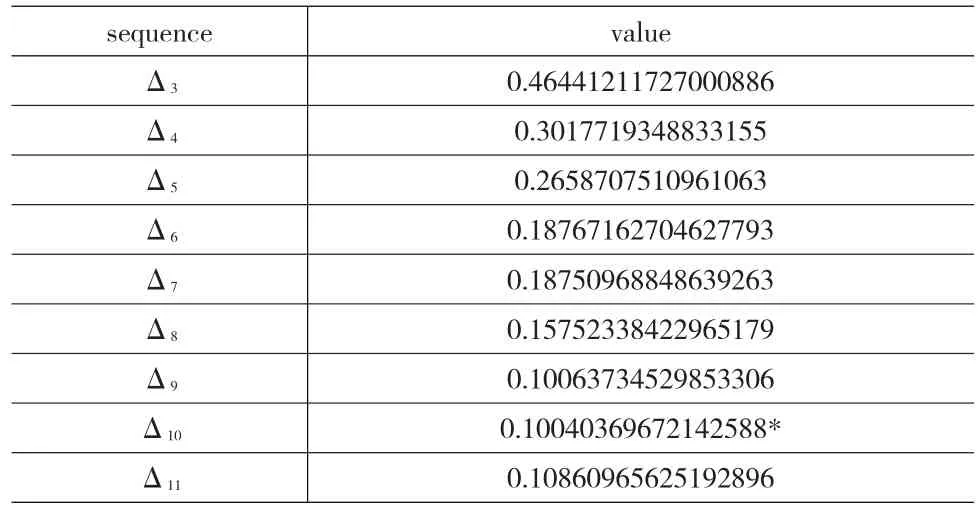
表3 乳癌数据集合聚类结果

由于Δ10是数列(Δ3,Δ4,…,Δ11)的极小值（实际上，Δ10也是第一个局部极小值），那么合理的聚类个数定为10。当聚类个数为10时，获得聚类结果如表4所示。

聚类结果由2个非常大的子类和8个很小的子类组成。8个很小的子类仅包含13个数据元素，它们依次是4,339,491;66,386;96;139;270;287;335,681,610;620。

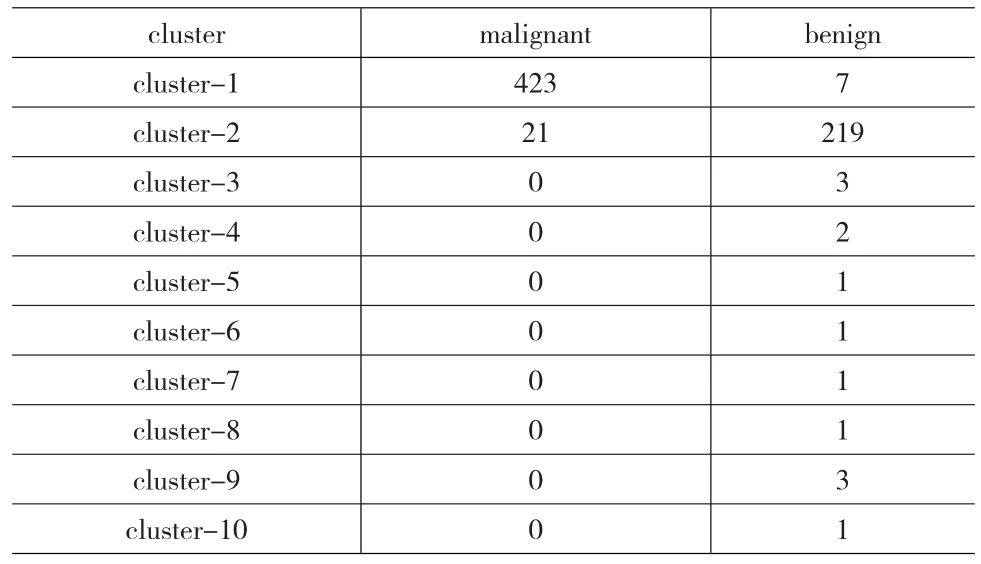
表4 聚类个数为10的乳癌数据集合聚类结果

同样地，以上两个较大的子类（cluster-1、cluster-2）对应良性组和恶性组，其准确率各自高达98.37%和91.25%。

3.3 动物园数据集合

动物园数据集合数据来源http://archive.ics.uci.edu/ml/ machine-learning-databases/zoo/，包含101种动物样本，每个样本有18个属性，属性1是动物名字，属性18是动物的分类编号（1,2,…,7）。属性14是腿的数目，取值集合为{0, 2,4,5,6,8}，本文也是把它视为类别型属性。其余属性是布尔取值集合{0,1}。

对于该数据集合本文获得如下数列(Δ3,Δ4,…,Δ9)，见表5所示。

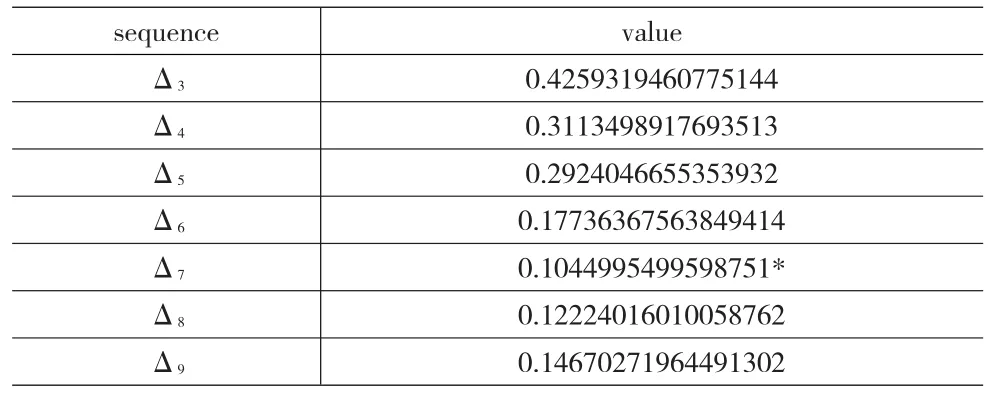
表5 动物园数据集合的数列

Δ7是上面数列的极小值，并且是第一个局部极小值。当聚类个数为7时，获得聚类结果见表6所示。

表6 聚类个数为7动物园数值集合聚类

类似于表2和表4，以上的聚类结果也是不错。例如，cluster-1中的38个数据对象，有37个属于class-1，仅有1个属于class-3。也就是，聚类结果的子类cluster-1中绝大部分元素正确地聚类到class-1中。特别地，聚类结果的子类cluster-3中的20个元素恰好与class-2完全一致。因此，该集合的聚类正确率也是相当高。

4 结论

类别型数据的聚类分析是数据挖掘中一项有意义的工作。基于质量和特征向量的聚类算法是对类别型数据集合聚类分析的一个新的研究方向。本文通过对3个类别型数据集合进行实验，验证本文的算法是有效的。

含有权重的特征向量构造是下一步的工作，对类别型数据间距离公式中参数修正、结合实际问题的合理选择聚类个数，以及聚类算法的有效性评价问题也是值得研究的问题。

[1]Han J,Kamber M.Data Mining:Concepts and Techniques,(2nd Edi⁃tion)[J].Elsevier Inc.2006.

[2]Xu R,Wunsch D I,Survey of Clustering Algorithms[J].IEEE Transac⁃tions on Neural Networks,2005,16(3).

[3]Yang M,Chiang Y,Chen C,et al.A Fuzzy K-partitions Model for Cat⁃egorical Data and Its Comparison to the GoM Model[J].Fuzzy Sets and Systems,2008,(159).

[4]Kim D,Lee K H,Lee D.Fuzzy Clustering of Categorical Data Using Fuzzy Centroids[J].Pattern Recognition Letters,2004,(25).

[5]Parmar D,Wu T,Blackhurst J.An Algorithm for Clustering Categori⁃cal Data Using Rough Set Theory[J].Data&Knowledge Engineering, 2007,(63).

[6]Chen D,Cui D,Wang C,et al.A Rough Set-based Hierarchical Clus⁃tering Algorithm for Categorical Data[J].International Journal of Infor⁃mation Technology,2006,12(3).

[7]Li T,Ma S,Ogihara M.Entropy-based Criterion in Categorical Clus⁃tering[M].Canada:Proceedings of the 21stInternational Conference on Machine Learning Banff,2004.

[8]Boutsinas B,Papastergiou T.On Clustering Tree Structured Data With Categorical Nature[J].Pattern Recognition,2008,(41).

[9]Ahmad A,Dey L.A Method to Compute Distance Between Two Cate⁃gorical Values of Same Attribute in Unsupervised Learning for Cate⁃gorical Data Set[J].Pattern Recognition Letters,2007,(28).

[10]Le S Q,Ho T B.An Association-based Dissimilarity Measure for Categorical Data[J].Pattern Recognition Letters,2005,(26).

[11]Pakhira M K,Bandyopadhyay S,Maulik U.Validity Index for Crisp and Fuzzy Clusters[J].Pattern Recognition,2004,(37).

[12]Chen K,Liu L.“Best K”:Critical Clustering Structures in Categori⁃cal Datasets[J].Knowledge and Information Systems,2009,(20).

（责任编辑/浩 天）

C931

A

1002-6487（2016）23-0069-04

国家社会科学基金资助项目(13GBL150);上海市自然科学基金资助项目(15ZR1401600)；福建省软科学项目（2014R0055）

赖芨宇（1962—），男，福建福州人，博士，教授，研究方向：数据挖掘、项目管理。

陈克明（1979—），男，江西新余人，博士研究生，副教授，研究方向：云计算、知识管理。