农业FDI对农业全要素生产率的异质门槛效应分析

马 巍，王春平，李 旭

（沈阳农业大学 经济管理学院，沈阳 110866）

农业FDI对农业全要素生产率的异质门槛效应分析

马 巍，王春平，李 旭

（沈阳农业大学 经济管理学院，沈阳 110866）

通过我国27省市的面板数据，采用门槛回归模型实证分析，发现开放经济环境下农业外商直接投资对我国农业全要素生产率影响具有非线性特征。实证结果表明：不同地区随着其开放度不同，农业FDI对该地区农业全要素生产率的影响也不相同，具体来说，出口依存度低于6.404%时，农业FDI对农业全要素生产率有负效应，在6.404%和21.715%之间，影响不显著，而高于21.715%时，农业FDI对农业全要素生产率有显著的正效应，农业FDI对农业全要素生产率影响呈现“U”型特征，而对外投资率存在单一门槛，当地区的对外投资率低于0.2955%时，农业FDI对农业全要素生产率有显著的负效应。

农业FDI；农业全要素生产率；对外开放；门槛模型

0 引言

近年来中国经济发展取得举世瞩目的成果，然而相对于快速发展的第二和第三产业，农业的发展明显落后。根据经济增长理论，经济增长的来源主要有两部分，即要素投入增加所带来的产出增长和技术进步所带来的全要素生产率的提高。但是我国正处于加速城市化的发展阶段，劳动力、资本都在迅速向城市转移，依靠要素投入增加以促进农业增长显然是难以实现的，因而农业技术进步带来的全要素生产率的提高才是农业持续发展的核心动力，解决我国农业问题的关键即是提高农业全要素生产率。

本文从对外开放角度，以我国27省市为研究对象，构造门槛回归模型，分析各省市在不同对外开放水平下，农业FDI对其农业全要素生产率的技术溢出效应，以期找出农业FDI在不同地区对农业技术影响存在差异的原因。

1 模型设计和数据来源

1.1 模型设计

1.1.1 门槛模型

为了避免人为划分不同经济发展层次所带来的偏误，本文选择Hansen（1999）提出的面板数据门槛模型，Hansen所给出的基本方程为：

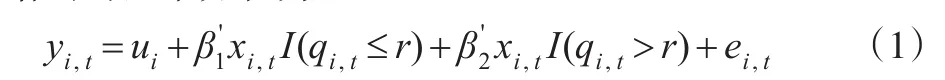
其中i表示地区，t表示年份，yi代表被解释变量，xi，t为机制依赖变量，ui反映个体效应，qi，t为门槛变量，r为要测算的门槛值，I为指标函数，ei，t是满足独立同分布于零均值等方差正态分布的随机扰动项。

为了能够得到估计参数，根据Hansen的做法，首先需要从每个观测值中减去其组内平均值，消除个体效应，得到的取代（1）式的yi，t，进一步将其写成矩阵形式为：，对于给定的r值，可以得到系数的估计值，则回归残差向量为，进而得到残差平方和，而最优门槛值就是使残差平方和最小，即

1.1.2 显著性检验

与传统采用交乘项计算门槛值的方法相比，Hansen (1999)的方法可以更好的对门槛效应是否显著，以及估计出的门槛值与真实值是否相等进行假设检验。

原假设为H0:β1=β2，备选假设为H1:β1¹β2，通过构造F统计量来检验：

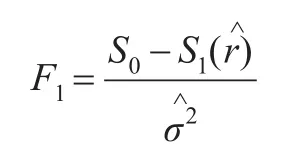
其中，S0为不存在门槛效应条件下，对模型进行回归估计得到的残差平方和。为存在门槛效应回归后的残差平方和由于此F值和经验P值无法从标准分布表中直接获取临界值，Hansen（1999）采用自抽样法进行多次可放回的重复抽样，计算原假设即不存在门槛效应模型出现的概率，得到基于似然率检验的p值和近似统计检验的临界值。如抽样的结果显示可以拒绝原假设，就可以认为模型存在门槛效应。

1.1.3 置信区间

在获得门槛值后再对门槛值与真实值是否相等进行假设检验，得到似然率统计量和参数估计的置信区间。原假设为H0:r=rÙ，相应的似然率统计量为：

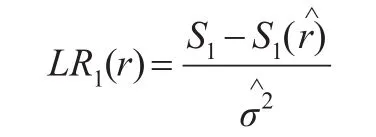
通过蒙特卡洛数据模拟分析，可以发现参数估计的置信区间的范围越小，其准确程度越高，门槛的估计值越接近真实值。对于似然率LR(r)指标，由于其不服从标准卡方分布，可以根据Hansen（2000）构建的门槛值非拒绝域（LR分布函数）来检验，当α在5%的显著性水平下，LR统计量的临界值为7.35。当门槛值所得到的LR统计量比临界值小的时候就可以认为估计得到的门槛值等于真实值。

1.2 回归模型

根据Coe和Helpman（1995）的观点一国的技术进步来源只有两种渠道，一方面是国内的研发，另一方面是从国外获得技术，因而构建出国际技术溢出的基本计量模型为：

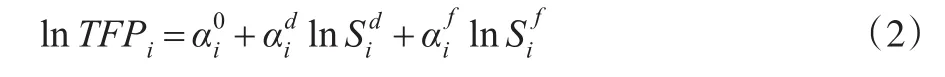
之后V-L（2001）将FDI也引入技术溢出模型中，证明外商直接投资对一国的全要素生产率也有重要影响，魏锴等（2013）也从理论方面论述了引进技术对我国农业发展的重要性。此外一些学者研究发现财政支农的力度会显著影响农业全要素生产率（方福前、张艳丽，2010；郑云，2011），因而将政府对农业的财政支持作为一个控制变量纳入到模型中，这样将（2）式转化为：

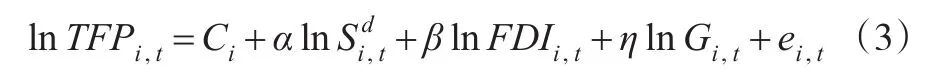
其中TFPi为农业全要素生产率；Sdi代表国内的农业R&D资本存量；FDIi，t为各省市农业外商直接投资存量；Gi，t为财政农林水支出存量，用以表示政府对农业的支持力度；ei，t同上。由此基于Hansen(1999)的基本模型，本文的单一门槛模型设定为：

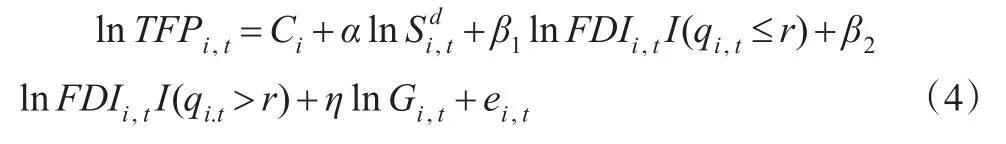
其中qi，t为门槛变量，用以衡量各地区的开放度；r为要测算的门槛值；I为指标函数。

1.3 数据的选取和处理

1.3.1 农业全要生产率的计算

本文被解释变量农业全要素生产率采用DEA的Malmquist生产率指数模型进行测算，对各项指标的选取采用王珏等（2010）的方法，主要包括：

产出指标：农林牧渔业总产值Y（亿元）。

投入指标：农业资本投入，包括各地区农用机械总动力x1（万千瓦）和化肥施用量x2（万吨）；农业劳动力投入用第一产业劳动力就业人数表示x3（万人）；土地投入用农作物总播种面积表示x4（千公顷）。

由于产出变量为农林牧渔业总产值，可能会受到价格因素的影响，因而以2007年为基期对产出指标进行价格调整。本文拟采用GDP平减指数对各省市农林牧渔业总产值进行价格调整，以剔除物价波动对全要素生产率的影响。

1.3.2 门槛变量

选择贸易开放度和投资开放度来衡量各地区的对外开放程度，贸易开放度的门槛变量设定为出口依存度，用各地区实际出口额占地区生产总值的比例来表示，投资开放度用对外投资率表示，用各地区对外直接投资额占地区生产总值的比例来表示。

1.3.3 其他变量的处理

本文数据来源主要来自于《中国统计年鉴》、各省市统计年鉴和《中国对外直接投资统计公报》，由于我国农业外商直接投资发展较晚，同时吉林、海南、四川和西藏的农业外商直接投资缺失，因而采用其余的27个省市2008—2012年的面板数据进行分析。

由于目前各省市（天津、上海、山东、重庆除外）统计数据中只有流量值，没有存量，这里采用黄凌云等（2009）的做法，对各变量的存量运用永续盘存法进行估算，其中FDI存量的经济折旧率，与张军等（2004）相同，采用固定经济折旧率9.6%；对于农业R&D投入的存量和财政农林水支出的折旧率采用C-H（1995）使用的5%计算；采用稳态方法对存量的基期值进行估计。

2 实证分析

2.1 回归模型的选择

由于本文选择的是面板数据，考虑到不同研究地区的个体效益，在回归分析中选择固定效应模型和随机效应模型，并进行hausman检验，以区分个体效应是被解释变量的解释变量还是仅仅是干扰项。检验结果的卡方值为19.29，P值为0.0002，认为个体效应是一个重要的解释变量，所以选择固定效应模型。

2.2 对外开放对农业FDI技术溢出的门槛效应

2.2.1 门槛值的确定和置信区间

根据Hansen（1999）的面板数据门槛回归理论，使模型残差平方和最小的r估计值，即要寻找的门槛值。采用Hansen在门槛回归中使用的“网格搜索法”搜索门槛回归中的候选门槛值r，之后利用Bootstrap法求解Bootstrap P值以确定门槛个数及适用的门槛区间，本文设定重复抽样1000次。

根据检验结果（表1和表2）可以发现，出口依存度对农业全要素生产率的影响存在双门槛效应，而对外投资率虽然在自抽样检验中单一门槛和双门槛模型都通过了假设检验。但是双门槛模型第一门槛的置信区间包含了第二门槛的置信区间，说明实际上对外投资率只存在单一门槛。因而，本文选取双门槛回归模型来分析出口依存度对农业FDI技术溢出影响的门槛效应，在分析对外投资率的影响时则采用单一门槛模型。

表1 门槛变量自抽样检验

表2 各变量门槛值和置信区间

2.2.2 农业FDI对农业全要素生产率影响的估计结果

表3列示了不考虑门槛效应，和分别考虑出口依存度门槛以及对外投资率门槛时的回归分析结果。

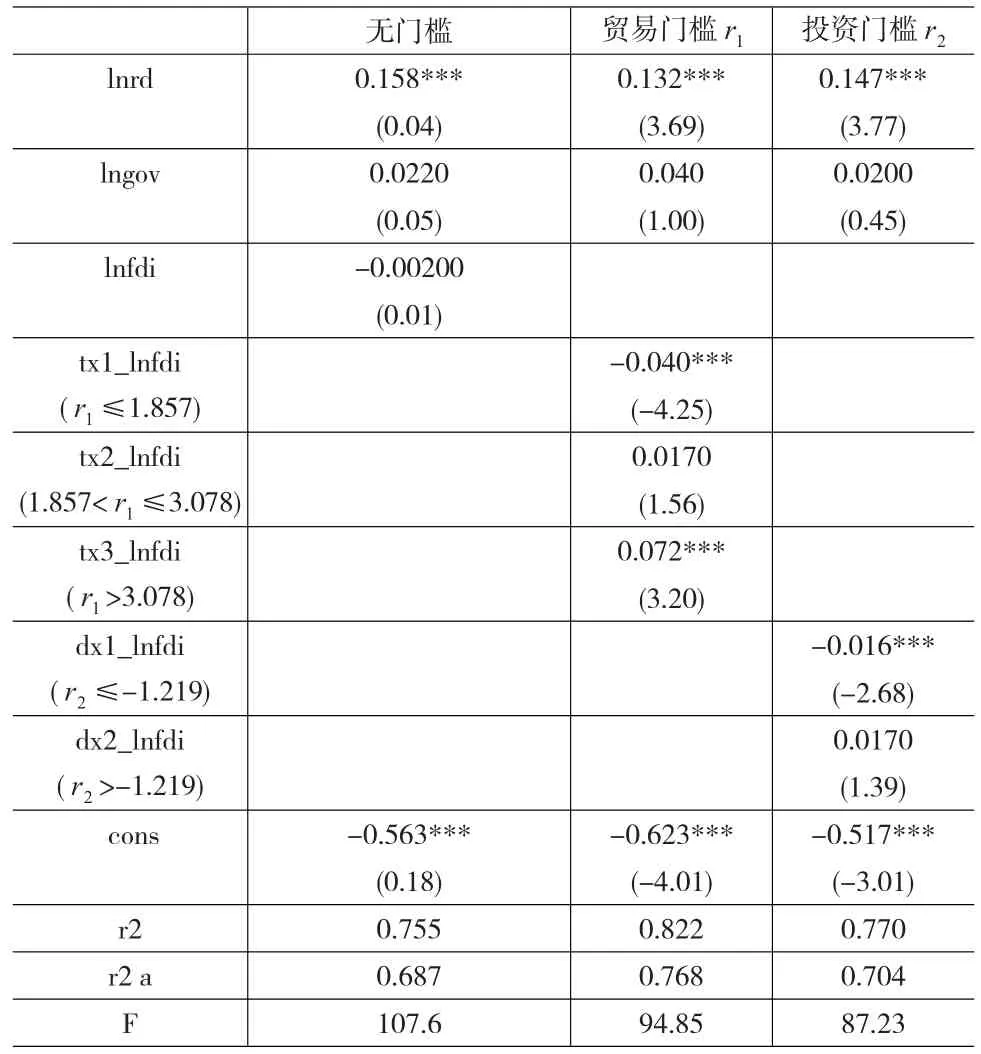
表3 不同开放度下农业FDI的技术溢出效应

从对比中可以发现在不考虑门槛效应时，农业FDI对农业全要素生产率的影响不显著，而无论是否考虑门槛效应，农业全要素生产率提高的主要来源都是科研的投入，政府对农业直接的财政补贴并不能显著的提高农业全要素生产率。而加入了门槛效应分析后，可以发现农业FDI对农业全要素生产率的影响呈现以下特征：

（1）出口依存度的第一和第二门槛值分别为1.857和3.078，模型中门槛变量进行了取对数变换，进行指数变换重新得到对应的出口依存度的实际值为6.404%和21.715%。当地区的出口依存度低于第一门槛值时，农业FDI对农业全要素生产率的影响是负的，系数为-0.04，并且通过1%水平的显著性检验，而当地区的出口依存度水平上升处于第一和第二门槛水平之间时，农业FDI对农业全要素生产率的影响则是不显著的，而对于那些出口依存度指标处于第二门槛值之上的地区，农业FDI对农业全要素生产率的影响呈现一个显著的正向影响，系数为0.072。说明在农业FDI对农业全要素生产率的影响有显著的门槛特征，随着出口依存度指标的上升，其影响总体上呈现出先负后正的“U”型。

（2）对外投资率门槛值为-1.219，进行指数变换得到对外投资率的实际值为0.2955%。对于对外投资率低于门槛值的地区，农业FDI对农业全要素生产率存在显著的负效应，系数为-0.016，而对于处于门槛水平之上的地区，农业FDI对农业全要素生产率的影响系数是正值，但是未能通过显著性检验，只有一个弱的正向相关关系，说明较低的对外投资水平制约了农业全要素生产率的提高，我国对外投资不足。

2.2.3 不同门槛区间的地区分布特征

图1和图2显示了各省市出口依存度和对外投资率的实际水平，以及对应的门槛值。为了更好的显示各地区在考察期的总体水平，选择各地区出口依存度和对外投资率的均值进行对比。

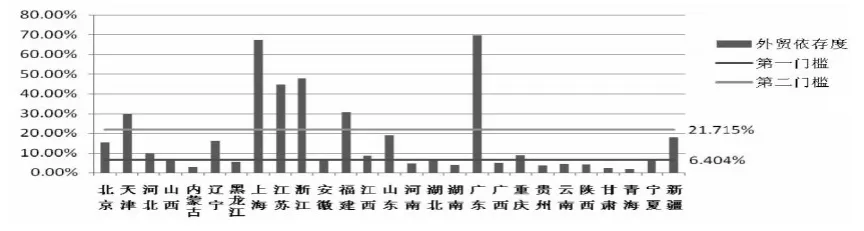
图1 各省市出口依存度均值

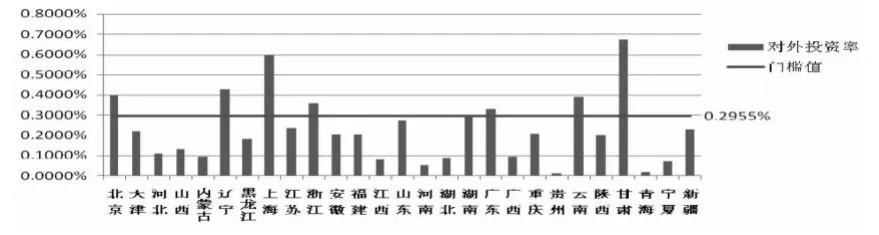
图2 各省市对外投资率均值

具体来看，在出口依存度门槛条件下，东部沿海的天津、上海、江苏、浙江、福建和广东等省市处于第二门槛水平之上，这些地区经济发达，对外开放度高，吸引来的农业FDI对农业全要素生产率有显著的促进作用；而北京、河北、辽宁、安徽、江西、山东、重庆和新疆的出口依存度则处于第一和第二门槛之间，这些地区农业FDI对农业全要素生产率的影响并不显著，这些地区有的属于东部沿海（如北京、河北、辽宁和山东），有的属于中部地区（如安徽、江西），甚至也包括了属于西部地区的重庆和新疆，但是从总体上来看这些地区虽然经济较为发达，但是相对位于第二门槛水平之上的六个省市，还是略差一筹，对外开放不足，无法从农业FDI中获得先进的技术；而对于处于第一门槛水平之下的省市（即山西、内蒙古、黑龙江、河南、湖北、湖南、广西、贵州、云南、陕西、甘肃、青海和宁夏），农业FDI不仅无法促进当地农业全要素生产率的进步，反而对农业技术的发展有一个负效应，抑制了这些省市农业全要素生产率的发展，这些地区对外开放度较低，使经济发展较为闭塞，与外部经济接触较少，农民对外来新技术的接受能力较差，不能很好的从外资中获得全部的技术溢出。而且这样农业外商直接投资更多的集中于农业领域中利润较高、发展较好的部门，对我国本土资本形成一种“挤出效应”，抑制了中西部内陆省份农业全要素生产率的发展。

在对外投资率门槛条件下，各省市多集中于低于门槛水平的区间，仅有北京、辽宁、上海、浙江、广东、云南和甘肃等省份位于门槛水平之上，而且对于位于门槛水平之上的地区农业FDI对农业全要素生产率仅有一个弱的正向相关关系。在研究对象中有74.1%的地区是位于门槛水平之下的，在这些地区农业FDI对农业全要素生产率的发展有负作用，阻碍了农业全要素生产率的进步，而对外投资率均值尚不足1%，也同样说明了我国目前面对投资难以“走出去”的问题。过低的对外投资率，使我国各省市只是单方面的接受外来资本，“有进无出”使技术溢出只存在于单一方向，而无法进行对外直接投资本身也说明了该地区的经济实力和技术水平未达到前沿水平，一味的被动接受外来资本，反而抑制了本土相关农业产业的发展，阻碍农业进步。

3 结论和政策建议

本文从开放视角探讨了农业FDI对农业全要素生产率影响的非线性特征，基于门槛模型分析法实证检验了2008—2012年我国27省市农业FDI对农业全要素生产率的不同作用，得到以下结论：

首先，出口依存度水平存在双重门槛，门槛值分别为6.404%和21.715%，对于出口依存度水平较低的地区，外来的农业外商直接投资抑制了当地农业全要素生产率的发展，而随着出口依存度的不断上升，农业FDI对农业全要素生产率的影响由负效应逐步转为正效应，门槛效应呈现“U”型特征。其次，对外投资率存在单一门槛效应，对于处于门槛水平0.2955%以下的地区，农业外商直接投资对当地的农业全要素生产率的发展存在负效应，农业FDI挤占了本地投资的发展空间，更多的表现为对我国农业全要素生产率发展的一种阻碍。

只有那些对外开放度较高地区，才可以从农业外商直接投资中获得正向的技术溢出，进而提高农业全要素生产率。而对于广大中西部地区的省市，农业外商直接投资虽然可以带来更为先进的技术，但受经济发展水平的限制，对外开放不足，无法从外资中获得技术溢出，同时农业外商直接投资多集中于农业领域中的高收入部分，对本地农业投资形成“挤出效应”，阻碍了本地企业对新型农业技术的研发，因而对于这部分位于门槛水平之下的地区，农业FDI事实上是阻碍了我国农业全要素生产率的提高。

由以上结论本文提出如下政策建议：农业是一国基础产业，农业问题也是我国经济发展中的重要问题，为了加快农业发展，提高农业全要素生产率的关键是依靠自主研发投入。在吸引农业外商直接投资时，对不同的地区应该区别对待。对于东部沿海开放度较高的地区，吸引外资可以从中获得技术溢出，在吸引外资时应将重点放在技术获取型外资上，以加大技术溢出效应。对开放程度较低的地区，政府应该鼓励其进行自主农业技术研发，对该地区的研究机构和研究企业给予财政上的支持，这比对农业进行直接的财政补贴更加有效。同时针对地区开放度不足的问题，政府应该对积极实行“走出去”投资战略的企业给予支持，鼓励出口贸易，使其达到门槛水平之上，以获得农业外商直接投资的技术溢出。

[1]Kohpaiboon A.Foreign Direct Investment and Technology Spillover:A Cross-Industry Analysis of Thai Manufacturing[J].World Develop⁃ment，2006，34(3).

[2]Hansen B E．Sample Splitting and Threshold Estimation[J].Econo⁃metrica，2000，68(3).

[3]罗军，陈建国.研发投入门槛、外商直接投资与中国创新能力——基于门槛效应的检验[J].国际贸易问题，2014，(8).

[4]孟令杰，李新华.FDI对我国农业全要素生产率的影响研究[J].农业经济与管理，2014，(1).

[5]杨向阳，童馨乐.FDI对中国全要素生产率增长影响研究的实证分析[J].统计与决策，2013，(3).

[6]魏锴，杨礼胜，张昭.对我国农业技术引进问题的政策思考——兼论农业技术进步的路径选择[J].农业经济问题，2013，(4).

[7]郑云.中国农业全要素生产率变动、区域差异及其影响因素分析[J].经济经纬，2011，(2).

[8]王珏，宋文飞，韩先锋.中国地区农业全要素生产率及其影响因素的空间计量分析——基于1992—2007年省域空间面板数据[J].中国农村经济，2010，(8).

（责任编辑/浩 天）

F323.3

A

1002-6487（2016）21-0130-04

国家社会科学基金一般项目（14BJY091）

马 巍（1985—），女，辽宁锦州人，博士研究生，讲师，研究方向：农业经济理论与应用。

王春平（1955—），男，辽宁沈阳人，教授，博士生导师，研究方向：农业经济理论政策与国际贸易。

李 旭（1975—），女，辽宁沈阳人，博士，副教授，研究方向：农村发展与农产品贸易。