空间误差分量模型的Bootstrap LM检验

梁凯乔，陈青青

（1.南京大学 广发银行博士后科研工作站，南京 210093；2.广东南方广播影视传媒集团有限公司，广州510012）

空间误差分量模型的Bootstrap LM检验

梁凯乔1，陈青青2

（1.南京大学 广发银行博士后科研工作站，南京 210093；2.广东南方广播影视传媒集团有限公司，广州510012）

空间误差分量模型（Spatial Error Components，SEC）传统的空间相关性LM检验存在严重的水平扭曲和较低的检验功效，导致检验统计量失效。文章将Bootstrap方法应用于SEC模型的空间相关性LM检验，提高检验统计量的有效性。Monte Carlo模拟实验表明，Bootstrap LM检验的水平受误差项分布、空间权重矩阵和样本量影响较小，并且远优于渐近LM检验，具有理想的检验水平；渐近LM检验和Bootstrap LM检验的功效均随着空间相关性的增强，及样本量的增大而增大，但Bootstrap LM检验在各种情形下均具有更高的检验功效，尤其是样本量较小时。简言之，Bootstrap LM检验是SEC模型更为优越的空间相关性检验方法。

空间误差分量模型；Bootstrap抽样；LM检验；Monte Carlo模拟

0 引言

空间经济计量模型已成为经济计量领域的重要分支和研究热点之一[1]，为处理经济运行中的空间交互作用和空间结构差异等问题提供了新的研究视角与分析工具。其基本思想是，将研究对象间由于地理位置邻近、经济条件接近等产生的空间相互关系引入经典的经济计量模型中。根据空间形式的差异，空间经济计量模型主要分为空间滞后模型（Spatial Lag，SLAG）和空间误差自相关模型（Spatial Error Autoregressive，SEAR），分别研究因变量和误差项中的空间相关性产生的影响。其表达式分别如下：

空间滞后模型（SLAG）：

y=Xβ+λWy+ε

空间误差自相关模型（SEAR）：

y=Xβ+ε，ε=ρWε+u

式中，W是空间权重矩阵，通常设定为地理空间权重矩阵，即研究对象为相邻区域，则对应的权重取1，否则取0。一般的，对W进行行标准化，λ和ρ为空间自回归系数。

Anselin（2001）[2]等文献对SLAG和SEAR模型进行了深入的研究，已基本解决经典经济计量模型的空间相关性检验和模型估计等问题。不过，Kelejian&Robinson（1993，1995）[3，4]指出，经典空间误差模型存在着两点不足之处：第一，在理论研究上，经典经济计量模型对空间相关性系数存在严格的限制条件，即 ||λ<1， ||ρ<1，如无法满足该假设，将导致误差项方差的奇异性以及误差过程的不稳定性，影响模型的检验统计量和参数估计方法的可靠性；第二，在实证研究上，经典空间经济计量模型假设模型中仅存在空间溢出效应，例如SEAR模型中，ε=(I-ρW)-1u，即假定对于某地区的所有误差冲击因素，都将由于空间相互作用而传导至邻近地区，未考虑到某些并未产生空间溢出效应的冲击因素，夸大了空间溢出效应。比如，在现实经济运行中，影响某一区域经济运行的因素异常复杂，其中，地理区位、环境污染等因素与邻近地区息息相关，将产生区域间的溢出影响，但本地政策、教育资源等一些因素则主要对本地区的经济产生影响，基本不产生溢出效应。经济计量实证研究中应全面考虑这两种不同的冲击因素。

为弥补经典空间误差模型的缺陷，Kelejian&Robinson（1993，1995）提出了空间误差分量模型（Spatial Error Components，SEC）：

y=Xβ+ε

ε=Wψ+ξ （1）

式（1）中，SEC模型的误差项方差Ω为正定矩阵，在理论上保证了模型误差项方差的非奇异性；此外，SEC模型的总误差项ε分解为两项相互独立的误差项，其中Wψ表示空间溢出的误差冲击（W为空间权重矩阵），ξ表示非空间溢出的区域特定冲击。可见，SEC模型弥补了经典空间经济计量模型的不足之处，是实证研究中更为合适的空间经济计量模型。

空间相关性检验是空间经济计量模型研究的前提。在SEC模型的检验研究方面，Kelejian&Robinson（1992）[5]在允许非线性、非正态等相对宽松的假设条件下，提出KR检验，可用于各种空间误差模型的空间相关性检验，但其用于SEC模型时缺乏有效性；Anselin（2001）提出了LM-SEC检验，但Monte Carlo模拟实验结果表明，即使在误差项正态分布或对数正态分布的条件下，LM-SEC检验仍然存在较大的水平扭曲和较低的检验功效；Carriazo& Coulson（2010）[6]试图修正KR检验，但Monte Carlo模拟实验结果仍证明LM-SEC检验优于修正的KR检验；Yang（2010）[7]修正了Anselin（2001）的LM-SEC检验统计量，提高了误差项非正态时检验的有效性，但是仍未达到理想的有限样本性质，此外，龙志和等（2013）[8]研究了面板数据空间误差分量模型的LM检验，但仅仅研究误差项为正态分布的情形，对于误差项为未知分布或异方差等情形未作深入探讨。简而言之，提高截面数据SEC模型的LM检验的有效性，使之达到较为理想的状态，是目前空间经济计量研究中有待解决的难题之一。

Bootstrap方法（Efron，1979）[9]是解决上述难题的有效途径之一。Bootstrap方法不需要进行误差项的分布假设或增加新的样本信息，只需根据给定的原始样本，进行多次有放回的重复抽样，通过复制观测信息，从而对总体的分布特性进行统计推断。Efron（2003）[10]进一步扩展了Bootstrap方法的使用范围和思想，使之适用于样本分布未知或者样本量较小的情形。龙志和等（2010）[11，12]等将Bootstrap方法应用于空间经济计量模型的Moran’s I检验、LM-Lag检验和LM-Error检验，模拟实验结果均显示，Bootstrap检验能有效的矫正渐近检验的水平扭曲，同时功效接近渐近检验，是有效的检验方法。

本文基于以上研究基础，将Bootstrap方法应用于空间误差分量模型的LM检验，解决渐近LM检验统计量失效的难题。

1 空间误差分量模型空间相关性检验

鉴于经典空间经济计量模型的不足之处，Kelejian& Robinson（1993，1995）提出SEC模型，其表达式如上文式（1）所示。式（1）中，假设：此外，假设误差项ψ和ξ相互独立，即E(ψiξj)= 0。则SEC模型误差项方差为：

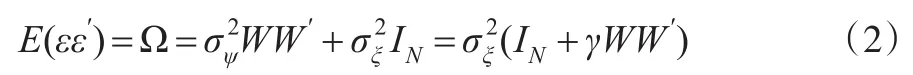
式中，IN为 N维单位矩阵，由式（2）可知，SEC模型的误差项方差Ω为正定矩阵，由此保证了误差项方差的非奇异性，解决了经典空间误差模型的困境。

在误差项正态分布的假定下，SEC模型的对数极大似然函数为：

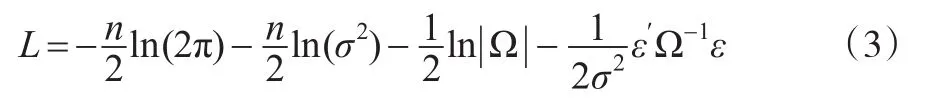
令θ=[σ2，γJ′，由于模型关于θ和β的信息矩阵是呈分块对角的形式，因此，进行空间相关性LM检验仅需计算关于θ的子信息矩阵。

根据Magnus(1978)[12]等研究，令导数向量（Score Vector）为d=¶L/¶θ，信息矩阵为，tr表示矩阵的迹。则：

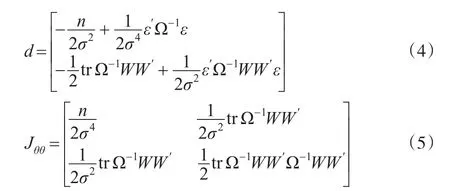
本文研究SEC模型的空间相关性LM检验，零假设H0:γ=0，备择假设H1:γ>0。根据LM检验的基本原理，得到：

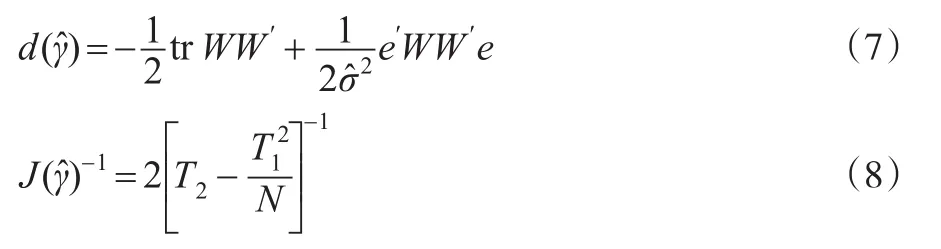
显然的，LMSEC～χ2(1)分布。尽管LM-SEC检验具有良好的大样本性质，但Anselin（2001）、Anselin&Moreno（2003）[13]通过Monte Carlo模拟实验研究表明，即使在误差项正态分布条件下，LM-SEC检验仍具有较大的水平扭曲，且在样本量较小或空间相关性较弱（γ较小）时，其检验功效也较低。

2 空间误差分量模型Bootstrap LM检验

Bootstrap方法是近年来发展较快的一种经济计量统计方法，它不需对研究对象的总体分布作任何假定，仅仅通过对已有样本进行等概率、有放回的随机抽样来产生新的样本，然后由大量的新样本构建总体的经验分布，逼近总体的真实分布，从而判断总体的统计特征。由于其宽松的假设条件以及有效性，Bootstrap方法被广泛应用于经济、金融等领域。本文将Bootstrap抽样方法应用于SEC模型的空间相关性检验，提高LM-SEC检验的有效性。

本文重点研究SEC模型在误差项正态分布、未知分布和存在异方差时，Bootstrap LM检验的有效性。文中采用残差Bootstrap[14]抽样方法来构造新的样本，进一步得到新的检验统计量及其经验分布。具体步骤如下：

②对N维残差e的进行有放回的随机抽样，每个样本被抽到的概率均等，由此得到新的残差e*；

③根据 y*=X+e*，由此得到一个Bootstrap样本(y*，X)；

④对新的样本(y*，X)再次采用OLS估计，得到残差e1，以及根据式（9）计算得到的Bootstrap LM检验统计量L*1；

⑤重复步骤②～④共B次，得到一系列的Bootstrap LM检验统计量

根据上述Bootstrap的执行步骤，得到Bootstrap LM检验的P值：

式中，I(x)是指示函数，若x表示的关系式成立，则I取值1，否则取值0。若Bootstrap LM检验的P值在一定的置信水平下拒绝原假设，则认为模型存在空间相关性，反之，则认为模型为普通的线性回归模型。

3 Monte Carlo模拟实验

本文Monte Carlo模拟实验参数设定如下：

（1）数据生成过程为：yi=α+xiβ+εi，i=1，...N。设定α=0.5，β=5；自变量方面，设定xi=10zi+si，其中zi服从[0，1]区间的均匀分布，si～N(0，1)。

①正态分布：ξ=σξ*rndn(N，1)

式中，rndn(N，1)为随机生成的N´1正态分布向量，σ2ξ为ξ的方差。

②未知分布：ξ=a*rndc(N，1)+(1-a)*rndt(N，1)

式中，rndc(N，1)和rndt(N，1)分别为随机生成的N´1维卡方分布和T分布，a为随机生成的0～1的小数，表示以a的概率选择卡方分布。

③异方差：ξ=σξ*rndn(N，1)×x

式中，符号×表示点乘，即rndn(N，1)和x中的元素一一对应的乘积。

（3）对于空间相关性参数γ的设定中，当设定γ=σ2ψ/σ2ξ=0时，本文考察LM检验的水平，当设定γ=σ2ψ/σ2

ξ=(0.5，1，4，8，16)时，本文考察空间相关性检验的功效。

（4）空间权重矩阵W设为Rook矩阵或Queen矩阵（Rook矩阵为研究对象间存在公共边时取1，否则取0，Queen矩阵为研究对象间存在公共边或公共点时取1，否则取0）。样本量方面，设定N=(25，49，81)。

本文模拟实验采用Gauss10.0软件进行编程，理论水平值设为0.05，模拟实验次数设定为2000次，Bootstrap次数设定为399次。本文重点比较各种设定下，渐近LM检验和Bootstrap LM检验的水平和功效表现，验证Bootstrap LM检验的有效性。一般的，检验水平值越接近理想值0.05（即水平扭曲越小），检验功效越大，表明检验统计量越优越。

3.1 Bootstrap LM检验的水平

设定γ=0，考察误差项为正态分布、未知分布或异方差情形，空间权重矩阵选取Rook和Queen矩阵，样本量选择N=25、49和81等设定下，渐近LM检验和Bootstrap LM检验的水平表现，如表1所示：

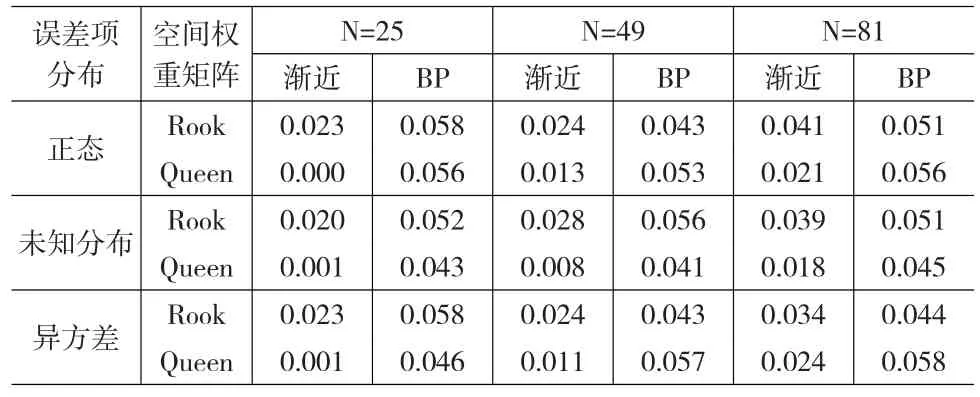
表1 渐近LM检验和Bootstrap LM检验的水平

由表1，从渐近LM检验来看，误差项为正态、未知分布或异方差对渐近LM检验的水平值影响不大，但是均存在较大的水平扭曲。使用Rook矩阵时，渐近LM检验明显具有更小的水平扭曲；而随着样本量的增大，渐近LM检验的水平扭曲逐渐缩小。Bootstrap LM检验方面，其检验水平值受误差项分布状况、空间权重矩阵和样本量大小影响不显著，均接近理论值0.05，并且其水平扭曲远远小于渐近LM检验，是更为有效的检验统计量。

3.2 Bootstrap LM检验的功效

设定γ=(0.5，1，4，8，16)，研究LM检验的功效。首先，考察正态分布下，渐近LM检验和Bootstrap LM检验的功效，如图1所示：

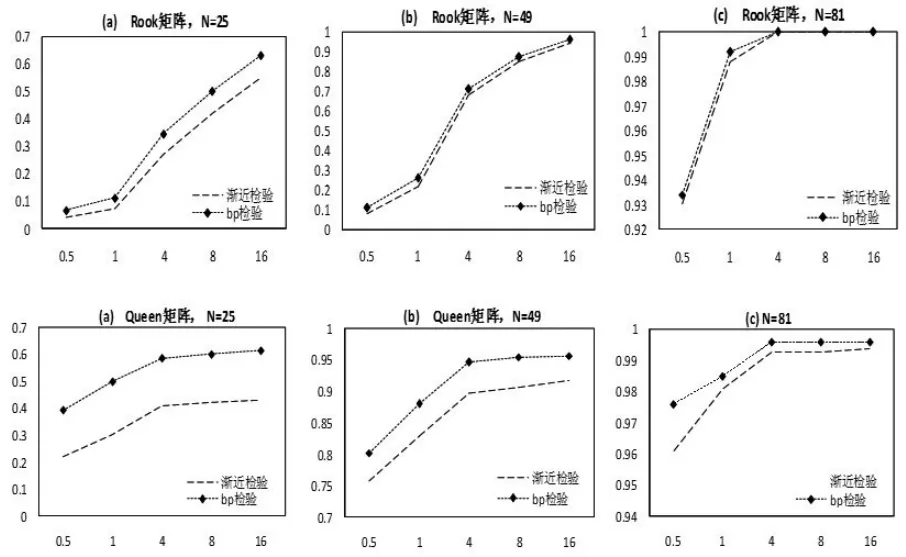
图1 正态分布下渐近LM检验和Bootstrap LM检验的功效

图1中，横坐标表示γ的变动，纵坐标表示功效值（以下皆同）。由图1，在误差项正态分布情形下，渐近LM检验和Bootstrap LM检验的功效均随着空间相关性（γ）的增强而增大，并且随着样本量的增大而增大。当空间相关性不强（γ=0.5）并且样本量较小（N=25）时，二者的检验功效均不理想，仅有0.1～0.4；而空间相关性较强（γ>4）且样本量较大（N=81）时，二者的功效均接近或达到理想值1；当空间权重矩阵使用Queen矩阵时，渐近LM检验和Bootstrap LM检验的功效通常要优于采用Rook矩阵。

此外，Bootstrap LM检验的功效在各种情形下都要优于渐近LM检验，尤其是在样本量较小或者使用Queen矩阵时，Bootstrap LM检验的功效显著大于渐近LM检验。表明在误差项正态分布情形下，Bootstrap LM检验具有更为优越的检验功效表现。

其次，本文以Queen矩阵，N=25和49为例，比较误差项正态分布和未知部分情形下，渐近LM检验和Bootstrap LM检验的功效。如图2所示：

图2 正态分布和未知分布下渐近LM检验和Bootstrap LM检验功效比较

由图2，各检验统计量的功效均随着空间相关性（γ）增强而增大，随着样本量的增大而增大。在误差项未知分布情形下，渐近LM检验和Bootstrap LM检验的功效均小于误差项正态分布时，但随着空间相关性的增强，正态分布和未知分布下的检验功效逐渐接近。两种LM检验统计量中，Bootstrap LM检验的功效要优于渐近LM检验的功效，尤其是样本量较小时（N=25），Bootstrap LM检验对渐近检验的功效有显著的优化。

进一步，本文以Queen矩阵，N=25和N=49为例，比较误差项正态分布和异方差情形下，渐近LM检验和Bootstrap LM检验的功效，如图3所示：

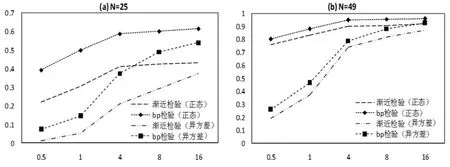
图3 正态分布和异方差下渐近LM检验和Bootstrap LM检验功效比较

由图3，不管是误差项正态分布或是存在异方差，渐近LM检验和Bootstrap LM检验的功效均随着空间相关性增强而增大，随着样本量增大而增大。当误差项存在异方差时，与误差项未知分布的情形类似，渐近LM检验和Bootstrap LM检验的功效均小于误差项正态分布时，但在空间相关性较强时接近。同样的，Bootstrap LM检验的功效要优于渐近LM检验，尤其是样本量较小时（N=25）。

4 结论

空间误差分量模型可弥补常见的空间滞后模型和空间误差模型在理论和实际应用上的不足，是实证研究中更为合理的空间经济计量模型。然而，空间误差分量模型传统的空间相关性LM检验存在较为严重的水平扭曲，以及较低的检验功效，影响其在实证研究中的有效性，本文将Bootstrap方法应用于空间误差分量模型的LM检验，试图弥补传统的渐近LM检验有效性不足的缺陷。Monte Carlo模拟实验结果表明，在检验水平方面，渐近LM检验具有严重的水平扭曲，尤其是使用Queen矩阵时，而Bootstrap LM检验则在各种参数设定下保持理想的检验水平表现；在检验功效方面，渐近LM检验和Bootstrap LM检验的功效均随着空间相关性增强而增大，且随着样本量的增大而增大。不过，不管是误差项正态分布、未知分布，还是存在异方差，Bootstrap LM检验均要优于渐近LM检验，尤其是当样本量较小时。总而言之，空间误差分量模型的Bootstrap LM检验矫正了渐近LM检验的水平扭曲，并且显著提高了检验功效，是更为有效的检验方法。

[1]Anselin L.Spatial Econometrics in RSUE:Retrospect and Prospect [J].Regional Science and Urban Economics，2007，37(4).

[2]Anselin L.Rao’s Score Tests in Spatial Econometrics[J].Journal of Statistical Planning and Inference，2001，97(1).

[3]Kelejian H H，Robinson D P.A Suggested Method of Estimation for Spatial Interdependent Models With Autocorrelated Errors，and an Application to a County Expenditure Model[J].Papers in Region Sci⁃ence，1993，72(3).

[4]Kelejian H H，Robinson D P.Spatial Correlation:A Suggested Alter⁃native to the Autoregressive Model[A].Anselin L，Florax R J.New Di⁃rections in Spatial Econometrics[C].Berlin:Springer，1995.

[5]Kelejian H H.Robinson D P.Spatial Autocorrelation:A New Compu⁃tationally Simple Test With an Application to Per Capita County Po⁃lice Expenditures[J].Regional Science and Urban Economics，1992， 22(3).

[6]Carriazo F，Coulson E.A Note on Testing for Spatial Error Compo⁃nents[J].Regional Science and Urban Economics，2010，40(5).

[7]Yang Z L.A Robust L M Test for Spatial Error Components[J].Region⁃al Science and Urban Economics，2010，40(5).

[8]龙志和，陈青青，林光平.面板数据空间误差分量模型的空间相关性检验[J].系统工程理论与实践，2013，（1）.

[9]Efron B.Bootstrap Methods:Another Look at the Jackknife[J].The Annals of Statistics，1979，7(1).

[10]Eforn B.Second Thoughts on the Bootstrap[J].Statistical Science， 2003，18.

[11]欧变玲，龙志和，林光平.空间滞后模型中Moran’s I统计量的Bootstrap检验[J].系统工程理论与实践，2010，(9).

[12]Magnus J.R.Maximum Likelihood Estimation of the GLS Model With Unknown Parameters in the Disturbance Covariance Matrix[J]. Journal Of Econometrics，1978，7(3).

[13]Anselin L，Moreno R.Properties of Tests for Spatial Error Compo⁃nents[J].Regional Science and Urban Economics，2003，33(5).

[14]MacKinnon J.Bootstrap Inference in Econometric[J].The Canadian Journal of Economics，2002，35(4).

（责任编辑/易永生）

F222.1

A

1002-6487（2016）21-0012-04

梁凯乔（1982—），男，广东广州人，博士后，研究方向：货币理论与政策、空间经济学。陈青青（1984—），男，湖南衡南人，博士，研究方向：空间经济学。